基于混沌粒子群算法的有轨电车车辆布局优化
2024-03-28王小涛周成林曹政文
金 林, 王小涛, 周成林, 曹政文
(1.湖南高速铁路职业技术学院, 湖南 衡阳 421200;2.中国铁建电气化局集团有限公司北京城市轨道工程公司, 北京 100043;3.湖南南岭衡阳民用爆破服务有限公司, 湖南 衡阳 421200)
0 引言
近年来,随着城市化进程的加快,越来越多的城市开始不断扩展轨道交通系统. 有轨电车作为重要的组成部分,其需求量日益增长. 车辆的设备布局直接影响车辆重心的位置,不科学的设备布局会造成车辆重心偏移过大,导致同一转向架的轴重差、轮重差偏大,进而影响列车牵引力和制动力性能的发挥,严重时甚至威胁行车安全. 因此,如何调整车辆的设备布局从而实现质量均匀分布,对于车辆的设计制造和行车安全有着重要的作用.
针对设备布局的优化问题,通常解决的步骤分为布局的建模和算法的求解. 沈健[1]提出了1种基于人与设备关系矩阵和设备之间的关系矩阵,对特种车辆的设备布局进行设计. 在布局优化的算法上,曹瀚[2]提出了1种基于遗传算法的电机控制器自动布局与优化,并以三相全桥逆变器作为算例验证了算法的有效性,但算法自身的稳定性较差. 黄辉嘉[3]以焊轨车为分析对象,采用粒子群算法对车辆的非固定设备布局进行优化,降低车辆的重心偏移量. 但粒子群算法自身容易陷入局部最优解,导致算法过早收敛.
目前针对有轨电车的设备布局研究较少,更多的依靠人为经验对布局进行优化,设计效率低下且盲目. 本文首先以有轨电车分析对象,提出了适用于有轨电车布局的数学模型,其次利用混沌粒子群优化算法化目标函数进行求解. 最后通过实例分析验证了数学模型和算法的有效性.
1 电车车辆布局数学模型
1.1 问题描述
有轨电车不同于动车地铁,由于车身离地面较低,大部分设备分布在车身上部. 有轨电车的设备布局优化的目标是调整部分设备的位置,以达到质量均衡分布在各转向架上,降低轴重与轮重偏差[4].
1.2 坐标系
在调整设备布局之前,首先对车辆建立笛卡儿坐标系,规定以车体纵向中心线为x轴,1位端为正方向,车体横向中心线为y轴,司机左侧为正方向,z轴起始于轨道平面,轨面法向为正方向. 坐标原点以2条中心线的交点,第1条中心线参考车体纵向,第2条中心线参考转向架的横向,2条中心线交点在轨面的投影即为坐标原点,如图1所示.

图1 有轨电车的设备布局图
车辆的设备种类繁多,且部分设备相对于x与y轴的转矩较小. 为简化计算,以3模块有轨电车为例,对所有设备力矩大小进行排序,将绝对值排行靠前的设备筛选出来,并去掉对称设备等,根据不同车辆,选出可适当调节的5个设备,如表1所示.

表1 可调节设备
根据可调节设备表可知,车辆设备布局就是调节这些设备的坐标,从而改变车辆的重心坐标,使得车辆的实际重心更接近于坐标原点,达到质量的均衡分配.车辆的设备分为可调节设备和固定设备,假设共有N个设备,固定设备的X方向总力矩为K,Y方向总力矩为H,可调节设备为n,此时车辆的重心公式为:
(1)
(2)
1.3 目标函数
根据实际情况,轨道车辆的轴质量、轮质量偏差主要取决于重心坐标的大小.其中x方向决定轴质量差,y方向决定轮质量差.因此,有轨电车的车辆布局优化问题可化为多目标规划问题,该问题的目标函数可归纳为求重心坐标绝对值的最小值:
(3)
(4)
1.4 约束条件
约束条件是在考虑实际情况后对搜索最优解的限制条件,以此限制变量的活动范围.设备的布局优化必须考虑在车辆边界干涉,设备维护、设备之间的干涉等相关因素,防止出现超出限界及设备之间发生相抗问题.
1.4.1 车辆边界干涉
设备在纵向调整过程中,不得超过车辆的边界.有轨电车的宽度设为L,调整量为Δy,设备的宽度为L1,则必须满足:
Δy≤|(L-L1)/2|
(5)
1.4.2 设备维护
考虑到后期在维护过程中,设备与设备之间需要一定的间距,假设设备之间的间距为T,则相邻设备重心坐标x之间差大于T:
|(X1-X2)|≥T
(6)
2 算法设计
粒子群算法是1种基于鸟群觅食行为的群体寻优智能算法,对于多变量且多约束的复杂问题,粒子群算法通过群体中个体之间的协作和信息共享,快速收敛至群体最优解处[5].然而,传统的粒子群算法由于种群的快速趋同效应,容易出现陷入局部极值的陷阱.针对这一问题,本文采用基于混沌思想的粒子群优化算法,利用混沌粒子的遍历性与随机性,提高种群的搜索能力,解决算法的早熟问题[6].
2.1 粒子群算法原理
在1个D维的空间中,我们假设存在N个粒子,这些粒子组成1个群体.在粒子群中,第i个粒子代表,其飞行速度用Vbest表示,其中Vbest={vi1,vi2,vi3…,viD}.第i个粒子找到的个体极值:Pbest={pi1,pi2,pi3…,piD}.整个种群搜索到的最优解为全局极值:Gbest={gi1,gi2,gi3…,giD},i取[1,N].之后粒子会按式(7)(8)更新自己的速度和位置:
(7)
(8)
式中,w为惯性权重;c1为自身学习的加速度;c2为社会学习的加速度;r1、r2为随机数,取值在0~1.
2.2 混沌粒子的优化
混沌粒子利用自身运动的特点,使得种群跳出局部最优,达到全局最优[7].本文采用Logistic映射混沌序列, 它可按照迭代公式进行反复的更新变换, 增强算法的随机性,
xn+1=μxn(1-xn)
(9)
式中,n为当前的迭代次数,当μ的取值比较靠近4时, 产生的是完全的混沌粒子,迭代所产生的值更适合组合优化.故
xn+1=4xn(1-xn)
(10)
混沌粒子本身的运动特性可帮助种群找到最优解.其寻找的核心为,先生成1组变量,该变量与优化变量数目相同.将该变量作为载体,引入优化变量,使其表现为混沌状态.其次开始遍历其运动范围,使其满足优化变量的取值,最后通过混沌变量进行搜索.基本步骤如下:
1)根据式(10)生成n个轨迹不同的混沌变量Zi= (Zi1,Zi2, …,Zin).
2)将Zi的各个分量载波到混沌扰动范围[-β,β], 扰动量Δx= (Δx1, Δx2, …, Δxn) , 生成新的粒子,其中
Δxj==-β+2βzij
(11)
xnew=gbestk+Δx
(12)
3)重新计算粒子的个体极值,若该极值小于全局极值,更新粒子的位置信息.
2.3 算法流程图
将混沌优化加入到粒子群算法中,得到混沌粒子群算法,其主要流程如图2所示.
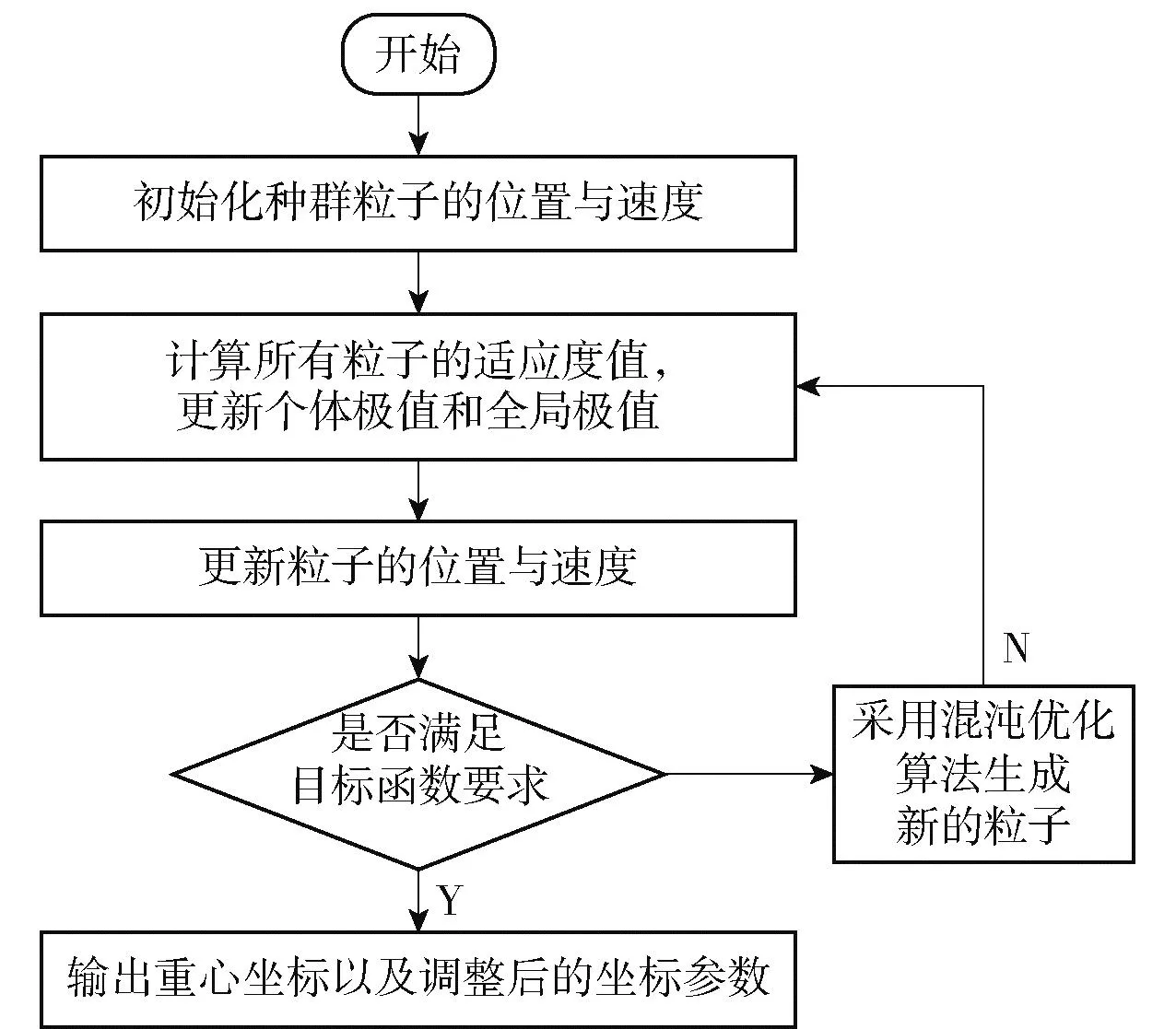
图2 混沌粒子算法流程图
3 实验验证
选取3模块有轨电车作为分析对象,数据来源于佛山有轨电车项目.以M1车为例,各个可调设备的初始参数如表2所示,此时车辆的重心坐标为(-4.06,1.56).
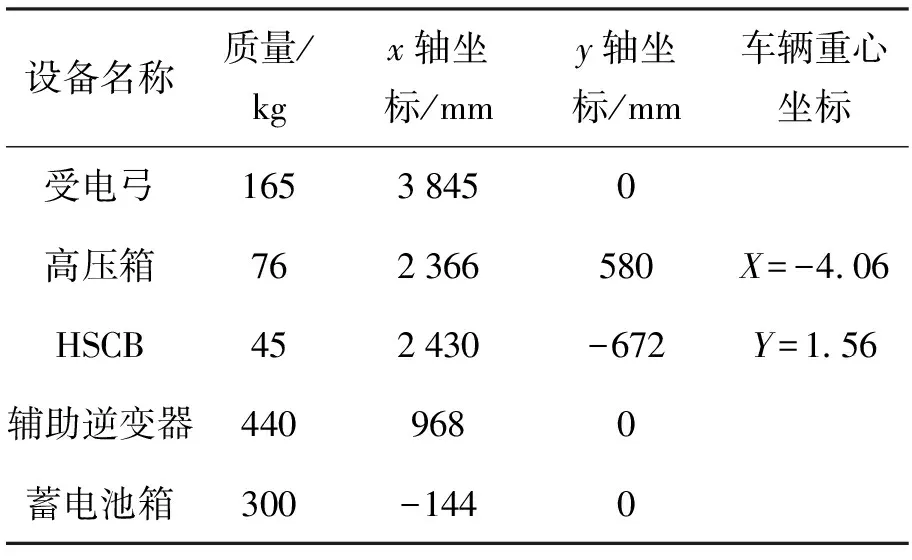
表2 可调设备初始参数
其次对算法参数进行赋值,其参数包含种群规模M,学习因子c1、c2、迭代次数ger,还应包含惯性权重w.设置种群规模为500,以找到最优解.为了提高算法的全局搜索能力以及局部搜索能力,使其达到最优,采用惯性权重实现.本文采用非线性动态惯性权重:
w=(wmax-wmin)((germax-ger)^(m-1)/germax^m)+wmin
(13)
式中,wmax为最大惯性权重,取值为0.9;wmin为最小惯性权重,取值为0.2;ger为迭代次数;m为控制因子,取值为6.
学习因子是用来调节个体和群体的学习能力,一般情况下,设置c1和c2数值都为2,最大迭代次数为100次.
为了验证算法的准确性和速度,同时采用蚁群算法进行对比结果.蚁群算法模拟自然界中蚂蚁觅食搜索路径的方法,常用于组合优化布局等场景.
算法优化后计算的结果如表3所示.

表3 优化后的设备参数
由表优化后的车辆重心坐标为(1.6,1.3),相比优化前重心坐标更接近坐标原点[8].相比于蚁群算法优化结果,其准确度更高.
由图3可知,车辆重心坐标X迭代37次算法收敛,最小适应度值为1.6,车辆重心坐标Y迭代39次算法收敛,最小适应度值为1.3.
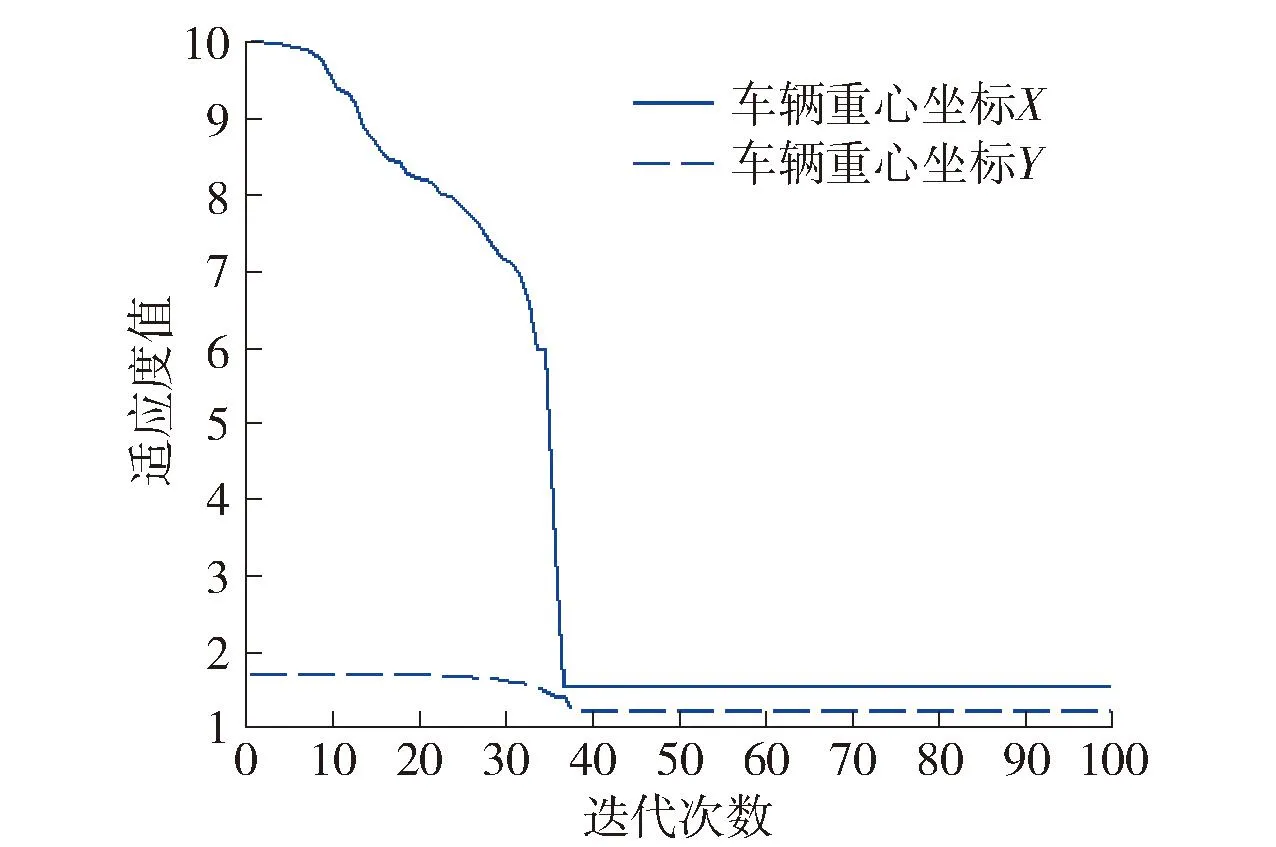
图3 适应度函数曲线
4 结束语
本文针对有轨电车车辆设备布局优化问题,以有轨电车为分析对象[9],首先建立了设备布局的数学模型,将布局优化问题转变为求车辆重心坐标绝对值的最小值,并给出相应的约束条件.其次,提出了1种混沌粒子群算法用于计算数学模型,其收敛速度快,效率高.实验证明,采用混沌粒子群算法优化后的车辆重心坐标相比优化前,与坐标原点的距离在x方向缩短了60%,y方向缩短了30%,显著改善了车辆重量的均匀分布[10].
