城市轨道交通列车碰撞动力学参数对爬车行为的影响
2024-03-27吴启凡王红伟肖守讷
许 娇 吴启凡 王红伟 肖守讷 王 尚
(1. 中车青岛四方机车车辆股份有限公司国家工程实验室(工程中心), 266111, 青岛;2. 中车南京浦镇车辆有限公司结构研发部, 210031, 南京;3. 西南交通大学轨道交通运载系统全国重点实验室, 610031, 成都)
随着城市轨道交通(以下简称“城轨”)列车速度的不断提高,人员伤亡事件发生的风险也随之提升,因此,列车运行过程中的耐撞性成为研究的重点。综合考虑到试验成本和现实条件,较少采用实车碰撞的方法获取试验数据。在列车耐撞性设计过程中,通常基于动力学理论,采用有限元和动力学仿真方法进行碰撞仿真。在列车耐撞性设计的初始阶段,根据运用工况、设计标准等仅能得到相关顶层参数,尚无法采用有限元仿真检验车辆设计的合理性。有限元方法存在建模复杂、计算周期长的问题;相比之下,参数化动力学方法[1]能节约数倍时间。在列车参数设计初期,运用动力学方法,可以提高其耐撞性设计效率。
文献[2-3]采用无质量的弹簧元件模拟非线性力,将其用于实际车体之间的连接,并将车体简化为质点,建立了初步的一维碰撞模型。文献[4]使用ADAMS(机械系统动力学自动分析系统)建立了车辆动力学模型,对列车发生褶曲行为以及横向初始条件进行了深入研究。文献[5]在考虑钢轨和轨道之间相互作用的基础上,完善了三维车辆动力学模型,并使用有限元方法同步建立了检验模型。文献[6]综合考虑了车钩缓冲装置的加卸载力学规律,以及吸能防爬装置等能量吸收主要区域对碰撞的影响,对车辆的点头振动和吸能结构垂向阻抗力进行研究;在SIMPACK软件中建立了车辆参数模型,研究了车辆在碰撞中的变化姿态。
国内外对城轨列车碰撞三维动力学模型的研究较少。本文将基于车辆-轨道(以下简称“车轨”)耦合动力学理论,将车体、转向架及防爬吸能装置等简化为相应的数学模型,在此基础上搭建列车碰撞三维动力学仿真平台并进行验证。同时对列车动力学参数进行筛选,研究其对列车碰撞过程中爬车行为的影响。
1 理论背景
1.1 车轨耦合碰撞动力学模型
本文基于文献[7]的车轨空间耦合模型中的动力学模型,以及文献[8]的适用于轨道交通车辆非线性碰撞的动力学模型,建立了列车碰撞三维动力学模型。本文将原模型按照实际碰撞过程中各部件之间的连接关系进行了调整,将各子部件简化为质点或力元,从而建立了车轨耦合碰撞动力学模型。
为了使计算的精度和准确度达到更好的平衡,在建立和简化模型的过程中进行了以下设置和简化:
1) 轮轨间做光滑处理,在主、被动列车之间设置40 mm的高差以模拟车辆正常运行中由于轮轨间激励产生的垂向错动。
2) 吸能防爬装置、悬挂装置及车钩缓冲装置等只考虑阻尼参数和等效刚度。
3) 轮对、构架及车体都为刚体,且质量集中于重心。
车辆模型由车体、转向架及轮对组成,且两两之间通过非线性弹簧元件与阻尼部件进行连接。完整的车辆模型总计38个自由度。
等效集总参数轨道模型以及弹性离散点支承模型广泛应用于商业多体动力学软件,适用于研究车辆与轨道之间的动态相互作用[8]。该轨道模型由地基轨枕和钢轨组成,其连接方式均采用阻尼元件和弹簧。整个轨道模型共12个自由度。
1.2 Hertz接触理论
在列车发生碰撞的过程中,碰撞力流和能量从车钩缓冲装置开始传递至车体。在垂向上,由于空气弹簧等悬挂结构主要承载车体部件,列车碰撞能量通过其传递至转向架,再通过轴箱等悬挂装置传递至轮对。车辆模型与轨道模型之间存在轮轨相互作用力,可通过Hertz接触理论计算轮轨间的弹性接触力。
1.3 刚体非线性连接模型
1.3.1 车钩缓冲装置模型
在列车编组中,车钩缓冲装置作为各节车辆间的基本连接部件,主要可将列车运行过程中产生的驱动力和制动力进行传递;而在列车中低速碰撞过程中,通过压溃管吸能结构的形变,可将列车碰撞过程中的冲击动能转化为内能,保护车体不受损伤。车钩缓冲装置的非线性迟滞特性曲线[9](见图1)包括压溃管曲线和缓冲器曲线,该曲线包含了二次加载和二次卸载的情况。
舟山电网是浙江省十一个地市电网中唯一的海岛电网,通过4回220 kV交流线路、3回110 kV交流线路和±50 kV直流线路与大陆电网相联,共拥有220 kV变电站5座,±200 kV柔性直流输电工程换流站5座,110 kV变电站28座,35 kV变电站26座,用户变26个[2]。

图1 车钩缓冲装置的非线性迟滞特性曲线
1.3.2 吸能防爬装置模型
吸能防爬装置作为列车碰撞过程中的第二级吸能结构,防爬齿啮合后,可有效防止两节车体之间的垂向错动,而吸能结构在变形中可将动能转化为内能。文献[10]的研究结果表明,吸能防爬装置的力学特性曲线可以采用纵向力-纵向变形量来等效。与车钩缓冲装置模型类似,吸能防爬装置的力学特性也可以采用非线性迟滞曲线来表示,见图2。

图2 吸能防爬装置的迟滞特性曲线
1.3.3 悬挂装置模型
一系悬挂装置和二系悬挂装置中,弹性连接元件的力学特性可以采用对应的刚度特性曲线和阻尼特性曲线来描述,如图3所示。

注:e1zc为一系悬挂装置的垂向压缩行程;e1zs为一系悬挂装置的垂向拉伸行程及其与限位止挡的距离之和;k1z1和k1z2为一系悬挂装置的第一、第二阶段垂向等效刚度;e2zc为二系悬挂装置的垂向压缩行程;e2zs为二系悬挂装置的垂向拉伸行程及其与限位止挡之间的距离之和;k2z1和k2z2分别为二系悬挂装置的第一、第二阶段垂向等效刚度。
2 列车碰撞三维动力学仿真平台
2.1 迭代算法
列车在碰撞过程中产生的自由度可达到数百个,传统的纽马克法等隐式算法在针对非线性铁路车辆系统的计算中误差较大。当车轨耦合碰撞动力学模型中涉及垂向非线性轮轨接触关系时,四阶龙格-库塔法等计算方法可能会出现虚假振荡,而精细积分算法能够保证很高的计算精度但计算效率偏低。文献[11]提出了修正双步长显式法,该算法的计算速度是四阶龙格-库塔法的4倍,且能够有效地解决列车非线性碰撞问题中车钩锁死的问题。
2.2 列车碰撞三维动力学模型验证
本文计算了列车碰撞三维动力学模型的对应工况。根据EN 15227:2020,该模型中主、被动列车均为4节编组。在碰撞速度为25 km/h的情况下,采用主动列车撞击静止的被动列车,并选取速度、加速度和轮对最大抬升量作为对比参数。同时采用列车碰撞有限元模型来验证列车碰撞三维动力学模型的精度。
结果显示:列车碰撞有限元模型和列车碰撞三维动力学模型计算的速度整体趋势比较接近,头车的车钩大约在0.25 s时发生了剪断;在0.60 s时,列车的整个碰撞过程结束,各节车辆速度都趋于同一个稳定值。在加速度方面,列车碰撞有限元模型中车辆加速度峰值出现在0.05 s左右,而列车碰撞三维动力学模型中车辆加速度峰值出现在0.03 s左右。在列车碰撞三维动力学模型中,将车体视为刚性质点;而在列车碰撞有限元模型中,将车体视为弹塑性体。因此,在车体纵向碰撞力流的传递过程中,其部件微小弹塑性变形的累加会导致延迟现象的产生。
图4为两种模型下的轮对最大抬升量-时间关系曲线。由图4可见:两种模型中轮对最大抬升量曲线随时间变化趋势十分接近,且其峰值的相对误差仅1.6%。相对于列车碰撞有限元模型,列车碰撞三维动力学模型并无弹塑性材料来吸收碰撞时产生的能量,所以该模型中轮对最大抬升量峰值会比列车碰撞有限元模型更早到来。

图4 两种模型下的轮对最大抬升量-时间关系曲线
3 列车碰撞动力学参数对轮对抬升量的影响
随着碰撞的进行,位于车辆端部的车钩部件率先被压缩。通常情况下车钩安装在其与车辆质心距离较大的位置,且存在较大的车钩轴向力,这种情况下会出现一个较大的作用力矩使司机室与客室出现点头转动;与此同时,由于车钩垂向偏转角的存在,车钩轴向力会产生垂向的分力将车体抬升。综合上述情况,车辆一位端的二系悬挂装置总体处于压缩状态,二位端的二系悬挂装置总体处于拉伸状态。随着车钩轴向力的进一步增大,以及两端拉伸和压缩状态的持续推进,处于拉伸状态的二系悬挂装置的空气弹簧达到其临界值接触限位止挡,此时由车体单独的垂向运动转化为车体带动转向架一起抬升。类似地,当处于拉伸状态的一系悬挂装置的空气弹簧达到其临界值接触限位止挡时,该装置弹簧拉伸产生的垂向力将轮对向上抬起,从而引发列车整体的爬车行为。
3.1 车间作用对轮对抬升量的影响
车间作用主要考虑了车间作用力和作用距离的影响。现设置头车吸能防爬装置作用力值为2 090 kN,车钩压溃管作用力值为1 030 kN,车钩缓冲器作用力值为930 kN;中间车车钩压溃管作用力值为930 kN,车钩缓冲器作用力值为830 kN。设置主、被动车高差为40 mm,吸能防爬装置以及头车、中间车车钩至车体质心的垂向距离均为1.3 m。以此为基准比率1,将车间作用力和作用距离设置在0.8~1.2的比率范围内进行研究。
头车车间作用力比率-轮对抬升量关系曲线如图5所示。由图5可见:头车车间作用力比率在0.8~1.2的范围内变化时,轮对抬升量总体呈上升态势;头车车间作用力比率在0.8~1.1的范围内变化时,轮对抬升量的变化逐渐趋于平稳;而当头车车间作用力比率处于1.1~1.2范围内时,轮对抬升量又出现了快速上升变化趋势。
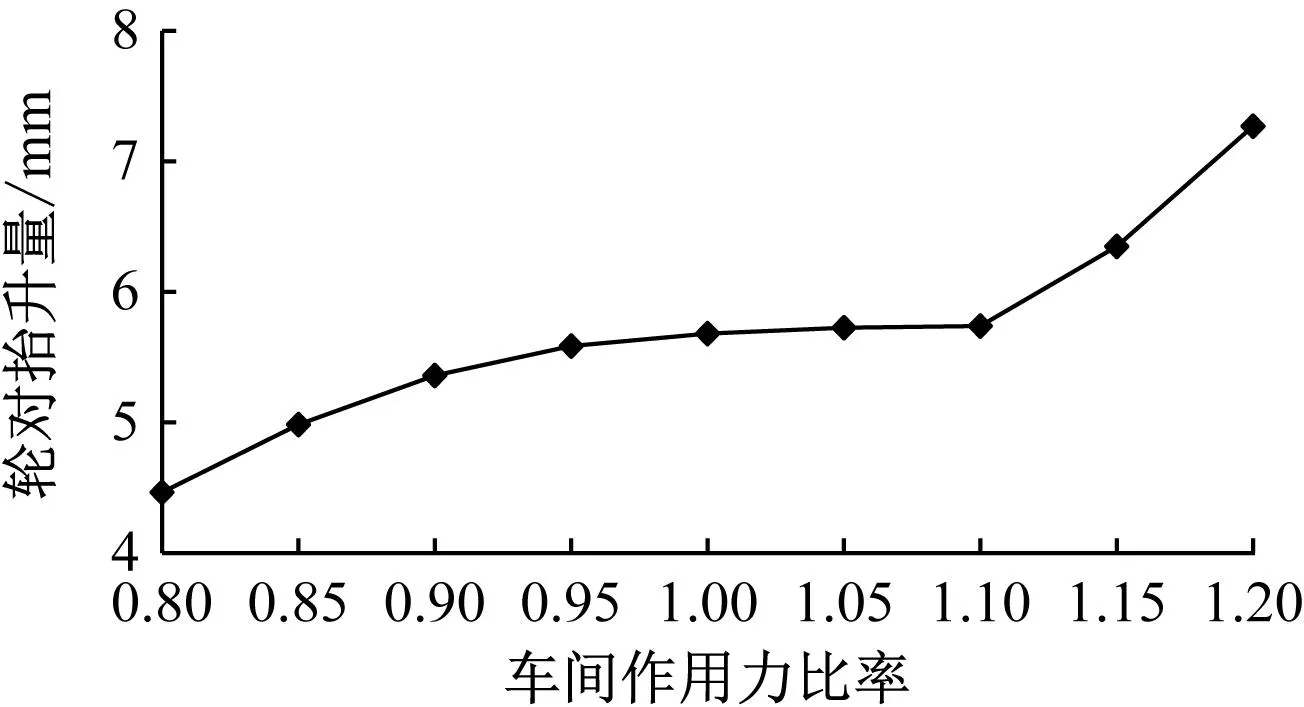
图5 头车车间作用力比率-轮对抬升量关系曲线
中间车车间作用力比率-轮对抬升量关系曲线如图6所示。由图6可见:中间车车间作用力比率在0.80~1.20范围内变化时,以比率为0.95作为分界点;当车间作用力比率在0.80~0.95范围内变化时,轮对抬升量的变化呈快速下降趋势;而车间作用力比率在0.95~1.20范围内变化时,轮对抬升量又趋于平稳,且曲线变化的极大、极小差值为2.8 mm。
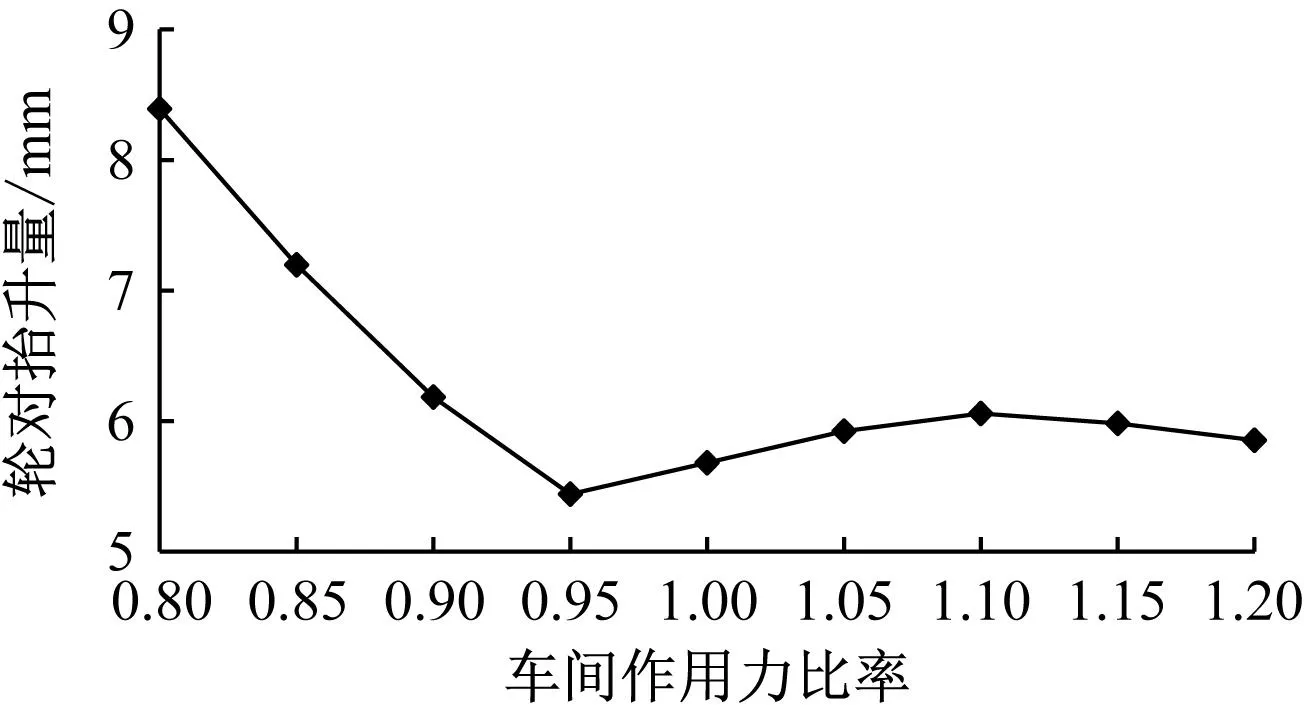
图6 中间车车间作用力比率-轮对抬升量关系曲线
主、被动车高差比率-轮对抬升量关系曲线如图7所示。由图7可见:主、被动车高差比率在0.80~1.20范围内变化时,轮对抬升量出现了比较稳定的增加态势,但提升幅度有限,轮对抬升量的最大变化量仅为0.17 mm,说明此项参数对轮对抬升量影响较小。
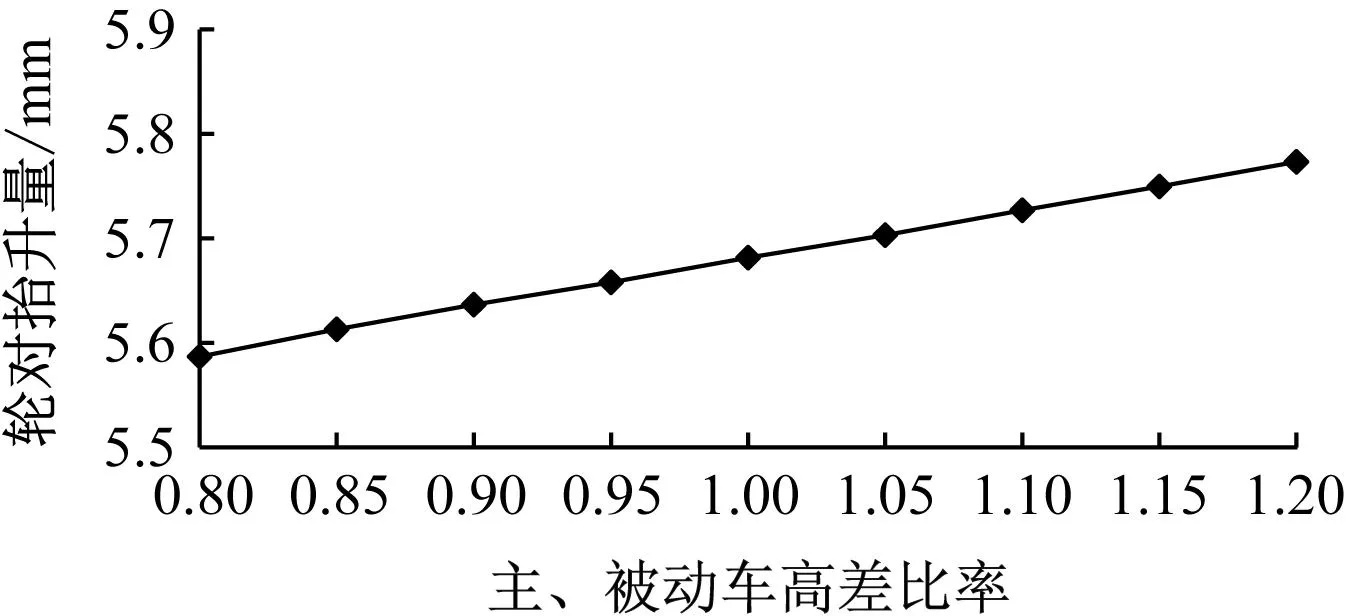
图7 主、被动车高差比率-轮对抬升量关系曲线
吸能防爬装置、头车车钩和中间车钩等的安装点(以下简称“安装点”)至车体质心的垂向距离比率-轮对抬升量关系曲线如图8所示。由图8可见:安装点至车体质心垂向距离比率在0.80~1.20范围内变化时,轮对抬升量出现了相对大幅度的提升,且其最大变化量达到了4.89 mm,说明此项参数对轮对抬升量影响较大。
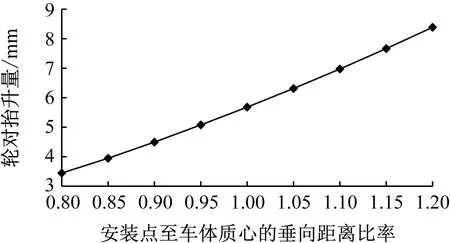
图8 安装点至车体质心的垂向距离比率-轮对抬升量关系曲线
3.2 车体参数对轮对抬升量的影响
在列车发生爬车现象的过程中,车钩缓冲装置和吸能防爬装置均对车体提供了点头转动力矩和垂向分力,其中点头转动力矩的大小取决于车钩部件与吸能防爬装置的安装点和车体的质心位置,而二系悬挂装置的行程变化量则与车辆定距密切相关。选取车体质量、车体质心高度和车辆定距等3项参数。车体质量设置为29 976 kg ,二系悬挂装置、车钩缓冲装置和吸能防爬装置至车体质心的垂向距离分别设置为1.41 m、1.30 m、1.30 m,车辆定距的一半为7.5 m。以此为基准比率1,设置0.8~1.2的比率范围进行研究。
车体质量比率-轮对抬升量关系曲线如图9所示。由图9可见:车体质量比率在0.8~1.2范围内变化时,以比率为1.1为趋势分界点,轮对抬升量先出现快速下降的趋势,随后逐渐趋于平缓,并在1.1时达到最低,之后则又出现了提升态势,其最大变化量约为7.43 mm,说明此项参数对爬车行为影响显著。
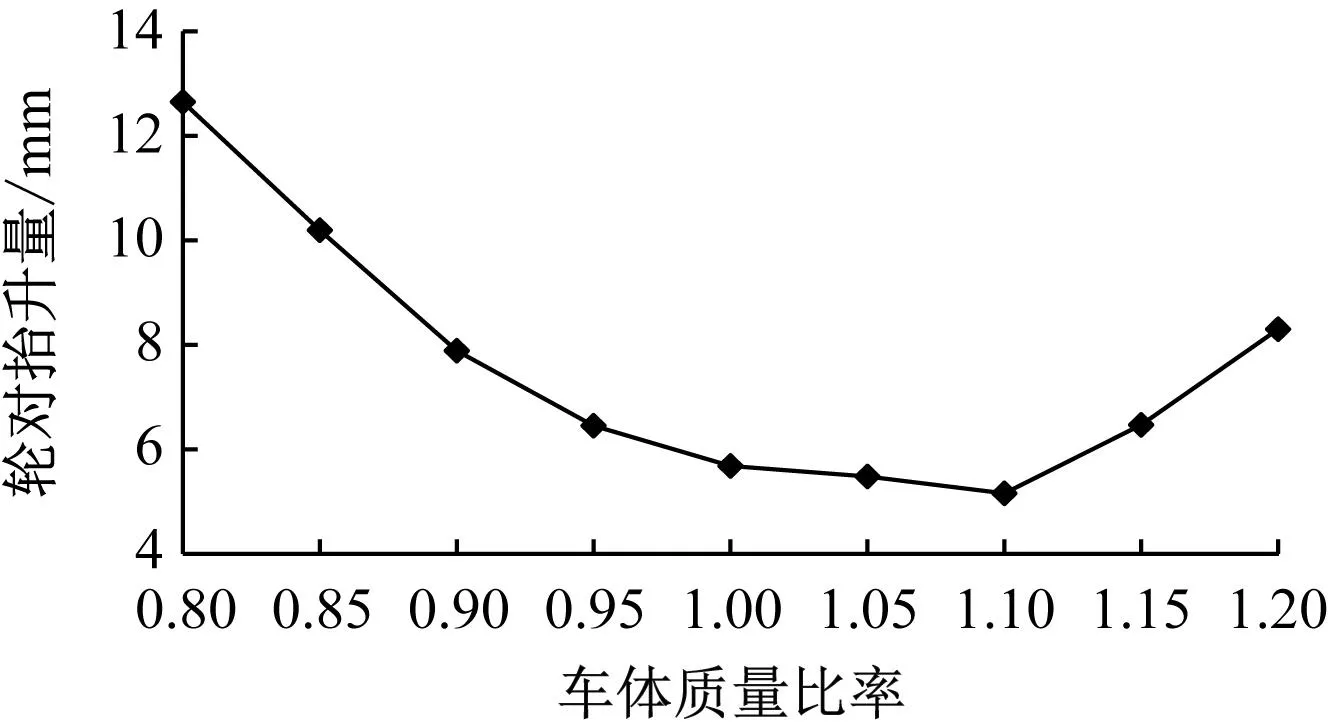
图9 车体质量比率-轮对抬升量关系曲线
车体质心高度比率-轮对抬升量关系曲线如图10所示。由图10可见:车体质心高度比率在0.8~1.2范围内变化时,轮对抬升量出现了较大幅度的提升,其最大变化量达到了4.81 mm,说明此项参数对轮对抬升量影响较大。车辆定距比率-轮对抬升量关系曲线如图11所示。由图11可见:车辆定距比率在0.8~1.2范围内变化时,轮对抬升量同样出现了较大幅度的增加,其最大变化量达到了2.65 mm。

图10 车体质心高度比率-轮对抬升量关系曲线

图11 车辆定距比率-轮对抬升量关系曲线
3.3 悬挂参数对轮对抬升量的影响
本文选取了一系悬挂装置和二系悬挂装置垂向刚度两种指标探讨其对轮对抬升量的影响。一系垂向刚度设置为1 298 600 N/m,二系垂向刚度设置为377 000 N/m,以此为基准比率1,设置0.8~1.2的比率范围进行研究。
二系悬挂装置垂向刚度比率-轮对抬升量关系曲线如图12所示。由图12可见:二系悬挂装置垂向刚度比率在0.8~1.2的范围内变化时,轮对抬升量出现了先快速下降后平稳降低的趋势;垂向刚度比率在0.8~0.9的范围内下降趋势较为明显,且其最大变化量达到了51.86 mm;而垂向刚度比率在0.9~1.2的范围内变化时,轮对抬升量下降趋势放缓,且其最大变化量仅为11.76 mm。因此,不难发现,二系悬挂装置垂向刚度对轮对抬升量影响很大。

图12 二系悬挂装置垂向刚度比率-轮对抬升量关系曲线
一系悬挂装置垂向刚度比率-轮对抬升量关系曲线如图13所示。由图13可见:一系悬挂装置垂向刚度对轮对抬升量的影响与二系悬挂装置垂向刚度截然相反,一系悬挂装置垂向刚度比率在0.8~1.2范围内变化时,轮对抬升量出现了比较均匀的上升趋势,且轮对抬升量的整体变化量为8.21 mm。由此表明,一系悬挂装置垂向刚度对于轮对抬升量影响较小。
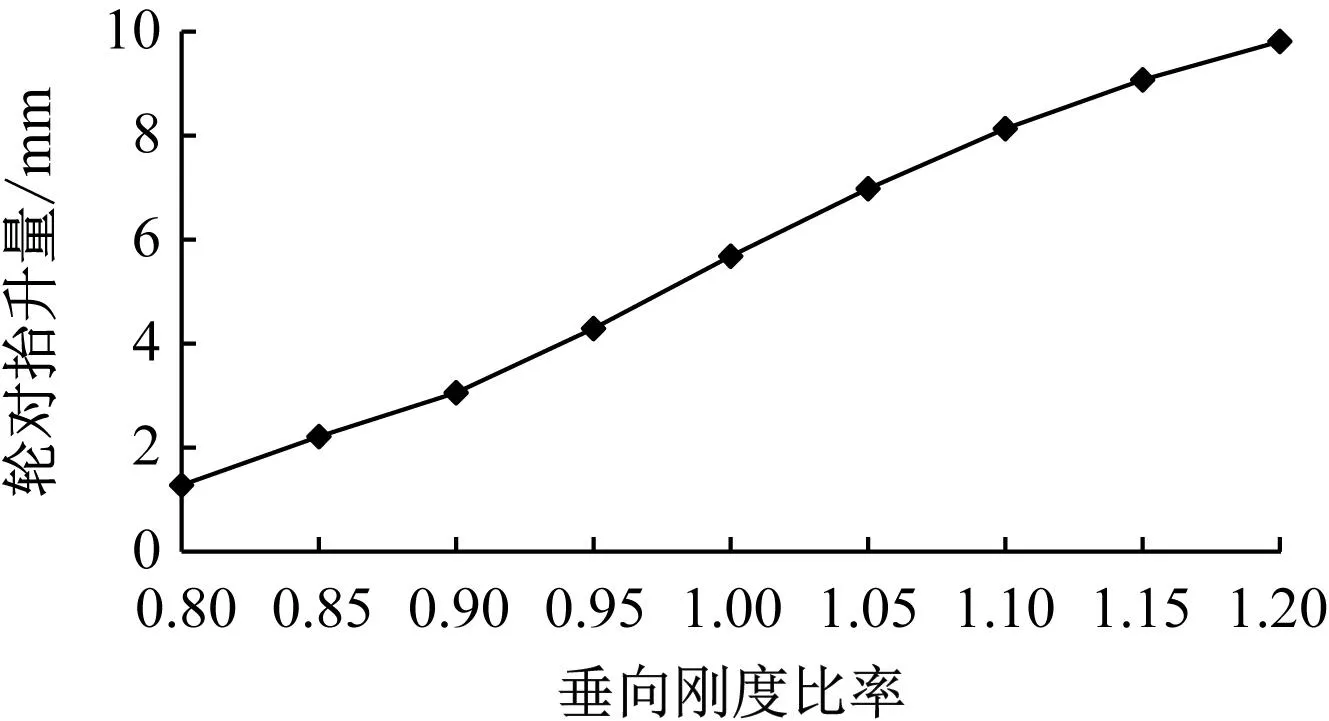
图13 一系悬挂装置垂向刚度比率-轮对抬升量关系曲线
3.4 列车碰撞动力学参数敏感度分析
为定性分析列车各项动力学参数对列车碰撞垂向响应的敏感度,采用比率为0.8~1.2范围内轮对抬升量的变化量表征列车碰撞垂向敏感度。将上述车间作用力、车体参数和悬挂装置涉及的9个参数的敏感度进行排序,最终挑选出5个敏感性较强的参数,分别是安装点至车体质心垂向距离、车体质量、车体质心高度、二系悬挂装置垂向刚度和一系悬挂装置垂向刚度。不同比率下的轮对抬升量如图14所示。

图14 各参数比率下的轮对抬升量
由图14可知:当参数比率在0.8~1.0范围内变化时,5个敏感性参数的排序依次为二系悬挂装置垂向刚度、车体质量、车体质心高度、安装点至车体质心垂向距离、一系悬挂装置垂向刚度;当参数比率在1.0~1.2范围内变化时,上述参数的排序依次为一系悬挂装置垂向刚度、安装点至车体质心垂向距离、车体质心高度、车体质量及二系悬挂装置垂向刚度。
4 结语
本文对城轨列车碰撞过程中的爬车行为进行了研究,建立了列车碰撞三维动力学仿真平台,并验证了其精度。基于所建立的平台,以轮对抬升量作为评价指标,研究了车钩缓冲装置等部件的车间作用力,以及车体参数对于列车发生爬车行为的影响程度,得到了二系悬挂装置垂向刚度、车体质量、车体质心高度、安装点至车体质心垂向距离及一系悬挂装置垂向刚度共5个敏感度较强的参数。当参数比率在0.8~1.0范围内变化时,二系悬挂装置垂向刚度和车体质量两项参数的敏感度较强;当参数比率在1.0~1.2范围内变化时,一系悬挂装置垂向刚度和安装点至车体质心垂向距离的敏感性较为突出。因此,在列车耐撞性设计中,应优先确定上述参数的取值,在此基础上进一步关联其他参数,从而获得列车参数对其碰撞响应的影响规律,可为车辆设计提供有益建议。
