基于关联离散变量的钢框架结构优化设计

葛晓凡 曲爽

(山东建筑大学土木工程学院，济南 250101)

引言

自我国改革开放以来，城镇化建设大多使用传统的钢筋混凝土结构，其在水泥和钢材的耗费量以及建筑垃圾的产生量上非常庞大，这种通过牺牲环境的传统发展方法已经无法满足现状甚至是未来的需求，想要完成建筑的可持续发展，则需找出真正健康并且适用于当前发展方向的方案，智能化、经济化、绿色化的钢结构建筑应运而生。相比传统的钢筋混凝土结构，钢材除了有环保、可回收的优点，更具有轻质高强、材质均匀、塑性、韧性更好等优势；同时，从资源的方面来看，2022 年我国产钢量为134 033.5 万t，在世界上位居首位，因此钢结构建筑在我国有着良好的发展前景。

结构优化设计是要在满足各种规范和特定结构性能目标的前提下，在结构的成本和收益之间达到平衡点。尺寸优化是结构优化最基本的形式之一，其优化对象是构件截面参数、模型的几何尺寸等。在现有型钢库中[1]，不同构件的截面参数是离散的、确定的，而相同截面的参数（如截面面积、惯性矩、截面高度）是关联的，在优化问题中可视为关联离散变量[2,3]。在钢结构建筑中，空间钢结构是目前应用较为广泛的结构形式，为推广其性能化设计，必须对空间钢结构进行整体结构分析的结构优化设计，使原结构更为经济、合理、安全。本文利用有限元软件Abaqus 的计算模块对某空间钢框架[4]进行分析计算，并使用Python 语言编写子程序对Abaqus 进行二次开发，利用计算机程序自动高效地完成了整个离散优化设计过程，得到了较为安全、合理、经济的设计结果。

1 结构优化分析过程

对结构进行优化设计时需要先建立该问题的数学模型，然后根据该模型的特征选取不同的优化策略，通过模型计算－数据验算－模型优化的循环过程求得最优解。Python 语言是一种面向对象的、解释型的、通用的、开源的脚本编程语言，在Abaqus 前处理和求解器之间使用的交互语言就是Python，同时在求解器以及后处理部分可以通过编写Python 子程序和脚本实现二次开发，故Python 语言可以完全满足对Abaqus二次开发的要求。本实验使用有限元分析软件Abaqus中提供的Python 接口编写优化分析的子程序，对模型进行离散参数化优化设计。

在结构优化问题中，凸优化问题较为常见，即在凸集中求解目标函数的最小化问题，对于凸优化问题基本的优化方法即进行迭代计算。在本次优化设计过程中，目标函数为求解结构总质量的最小值，故本文的优化方法采用迭代优化方法，通过对目标函数逼近将约束的优化问题转换为非约束的优化问题，从而求解离散优化问题的全局最优解。该方法适用于空间钢框架的结构优化设计，流程图如图1 所示。通过验算模块会得到两个包含构件验算结果的列表（succeed_part、failed_part），当模型总质量连续三次收敛后，程序会停止迭代计算，出于安全性的考虑，程序会在第三次收敛后对模型失效的构件进行增大设计，使该构件的截面面积增大并再次进行验算，最终得到一个安全、经济的优化结果。

图1 结构优化框架流程图

2 结构优化设计数学模型及分析

2.1 问题描述

某缩尺二层钢框架，构件均受竖向荷载，构件的受荷情况以及初始参数如表1、表2 所示，模型的几何布置图和构件布置图分别如图2、图3（a）~（b）所示。

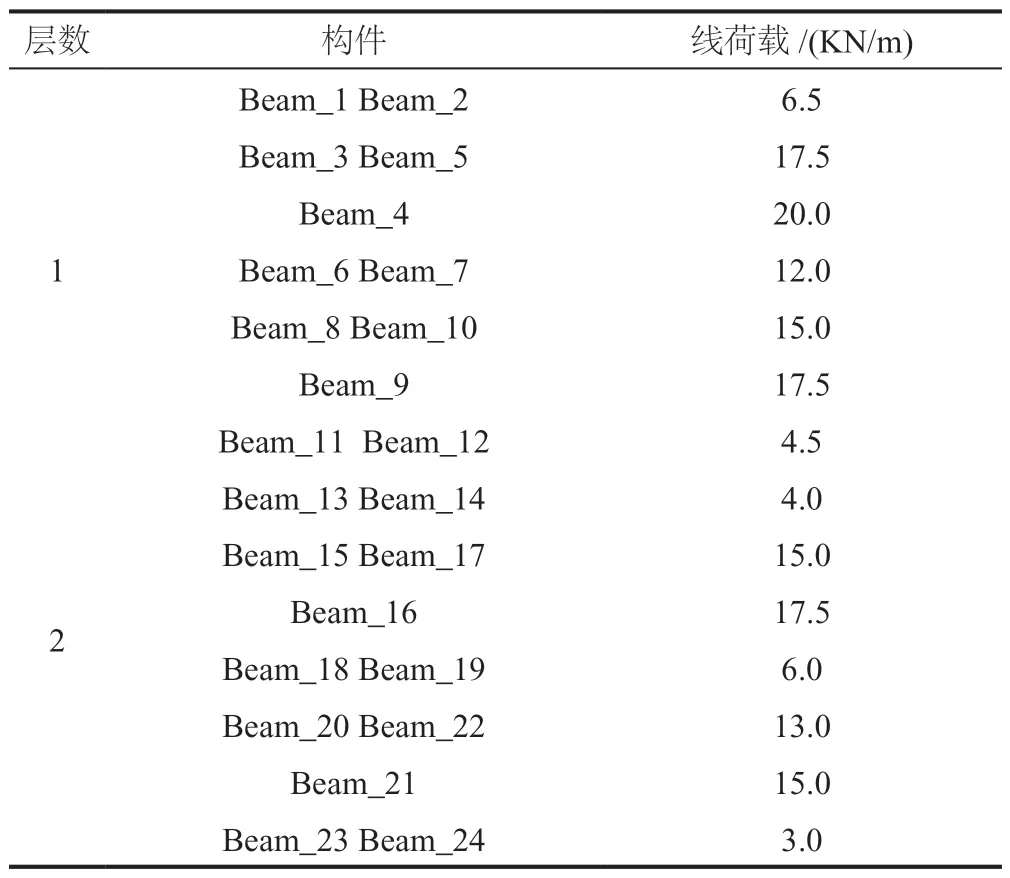
表1 构件受荷情况

表2 初始构件参数

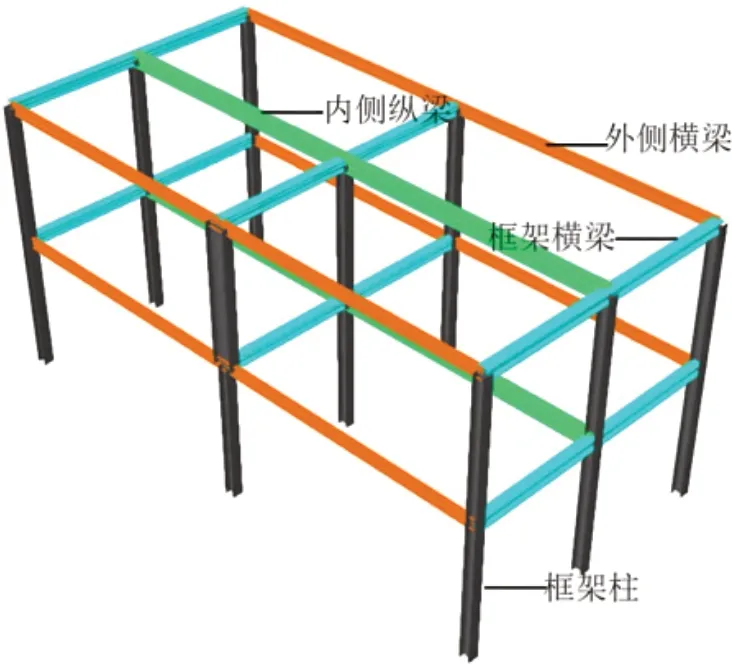
图2 有限元几何模型

图3 构件布置图（单位：mm）

2.2 材料参数

弹性模量：E ＝2•06×105MPa

泊松比：v ＝ 0.3

密度：ρ ＝ 7 800kg/m3

常温强度设计值、常温屈服强度值：根据钢结构设计规范[5]取值；

钢材本构模型：选用二次塑流模型作为钢材本构，具体公式见文献[6,7]中内容。

2.3 空间钢框架结构优化设计的数学模型

进行结构优化设计首先要建立实际工程问题的数学模型，然后选择合适的优化策略，一般来说，一个优化问题主要有目标函数、设计变量、约束条件三个要素。现行规范中多采用极限状态设计法，一般来说，极限状态设计法可将结构的极限状态分为承载力极限状态和正常使用极限状态，当结构超过承载力极限状态，即结构发生了破坏[8]：

本次优化问题以结构可靠性为约束条件，即对于钢框架梁，在结构设计中属于受弯构件，以其强度、整体稳定、挠度作为极限判别标准；对于钢框架柱，在结构设计中属于压弯构件，以其截面强度、稳定性作为极限判别标准。

杆件的各类截面参数如截面面积、回转半径、惯性矩、高度等是相互关联的[1]，选定其中一个截面参数代表其相同截面的其他参数也被选定，故称为关联离散变量[2,3]。将规范型钢库中的H 型钢的截面参数按截面面积大小排序，共得到130 个截面参数的集合：

式中：S为标准截面构成的集合：为第i 个标准型钢的截面参数的集合。文献[9-12]中采用0-1 规划处理关联离散变量。

ti为0-1 变量，表示第i 个截面是否被选中，选中则取1，否则取0，本质上是表征标准截面集合S 与构件截面参数之间的映射关系。综上所述，本文以空间钢框架总质量为目标函数，构件截面参数y 为设计变量，模型杆件的长度已经确定，实际上本次优化问题是在满足结构可靠性下的构件最小截面面积问题，数学模型如下：

式中:ρ为钢材密度,yj表示模型第j 个构件的截面参数

约束条件：

空间钢框架梁：

空间钢框架柱：

式中，

Mx、My——同一截面处绕 x 轴和 y 轴的弯矩

γx、γy——截面塑性发展系数

Wnx、Wny——对 x 轴和 y 轴的净截面模量；

Wx、Wy——对 x 轴和 y 轴的毛截面模量；

f——钢材的抗弯强度设计值

ϕb——梁的整体稳定性系数

V——当前构件最大挠度

lj——第j 个构件的计算长度

N——所计算构件范围内轴心压力设计值

ϕx、ϕy——对强轴和弱轴的轴压构件稳定系数

ϕbx、ϕby——考虑弯矩变化和荷载位置影响的受弯构件整体稳定系数

η——截面影响系数，工字型钢为开口截面η取1.0

βmx、βmy——等效弯矩系数

N'Ex、N'Ey——取N'Ex、N'Ey=π2EA/(1.1λ2)

λ——强轴、弱轴长细比

An——当前截面净截面面积

A——当前截面毛截面面积

下面将介绍构件截面的优化过程。以BEAM_1为例，BEAM_1 在优化前的位移云图如图4（a）所示，此时其截面在型钢库中的编号为12，截面面积为16.68m2，当程序判断BEAM_1 失效时会将该构件在型钢库中的编号加一，如图4（b）所示，此时BEAM_1的编号为13，截面面积为17.58m2，通过对比优化前后的位移云图可以看出跨中位移明显降低；同样当程序判断构件满足验算后，会将该构件在型钢库中的编号减一，减小截面面积，从而达到减少用料的目的。

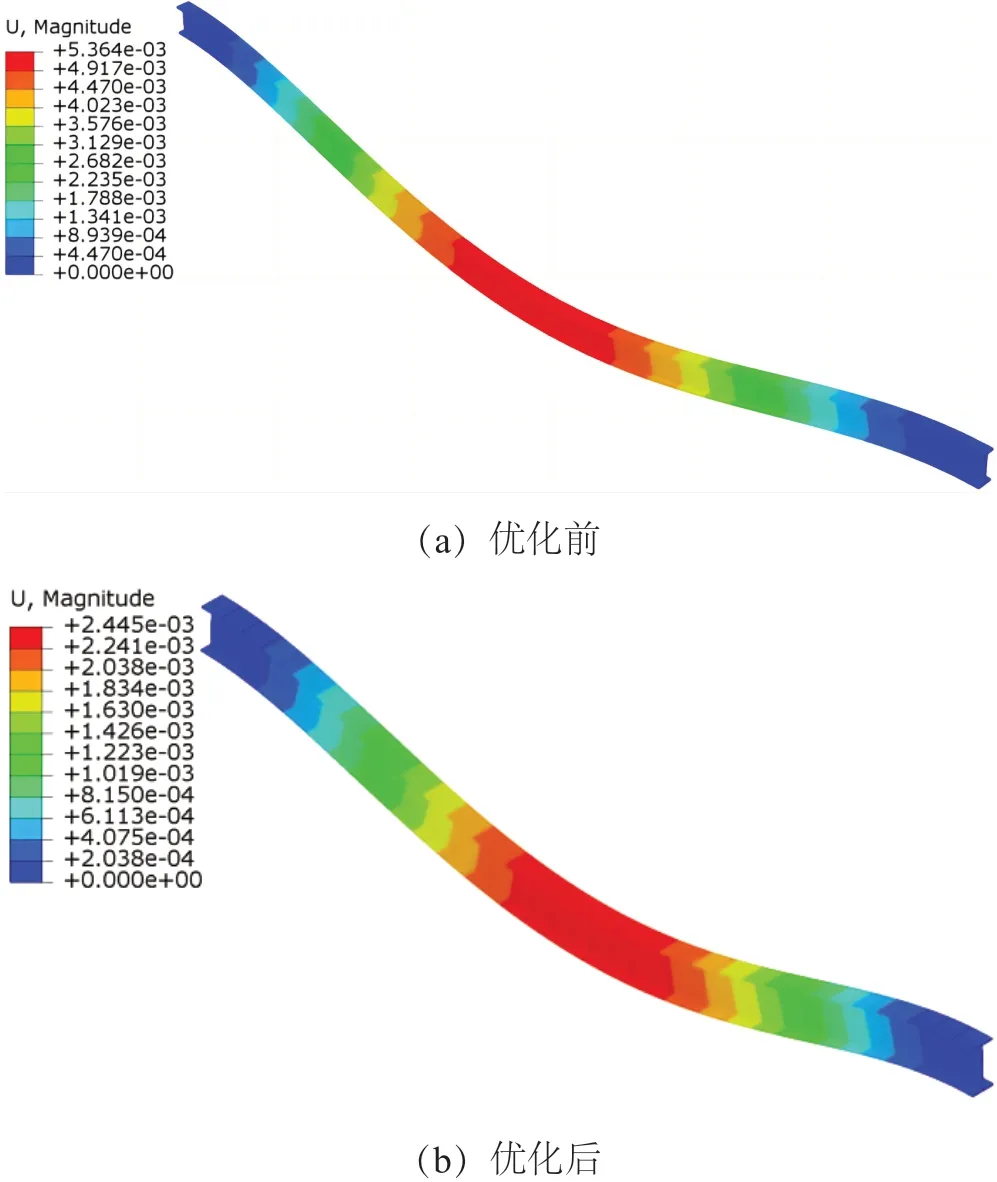
图4 构件优化前后位移云图（单位：m）

2.4 计算模型

在Abaqus 中，在对大型结构进行分析时，当构件的横截面的尺寸相对于长度较小时，可以简化为梁单元进行分析，相比于实体单元，梁单元的计算速度更快，且在结构优化的过程中，关注的重点是模型的力学行为，故使用梁单元作为模型的单元类型。Abaqus有两类梁单元，即欧拉－伯努力梁（B23、B23H、B33等）和铁木辛克梁（B21、B31 及对应的杂交单元等），其中铁木辛克梁允许横向剪切变形，适用于短梁，而欧拉－伯努力梁不允许横向剪切变形，对于长梁可以采用欧拉－伯努力梁，对于短梁可以使用铁木辛克梁，而介于长梁和短梁之间的构件，两种单元的计算结果区别较小[13,14]。文中模型的构件多为长梁，故结构分析采用B33 单元，即三次梁单元，模型使用米单位制。为保证模型计算精度，布种密度为0.1，模型共有1 065个结点，1 080 个梁单元。计算时，每个结点均有x、y、z 三个方向的转角和位移，梁柱结点均采用刚性连接，荷载均为竖向的均布荷载。在模型中，x 轴为较长跨方向，y 轴为框架高度方向，z 轴为较短跨方向，框架底层的柱脚三个方向的转动、位移均被约束。分析步采用静力通用分析，输出变量为结点应力、截面轴力和弯矩、结点位移，计算分析模型如图5 所示。

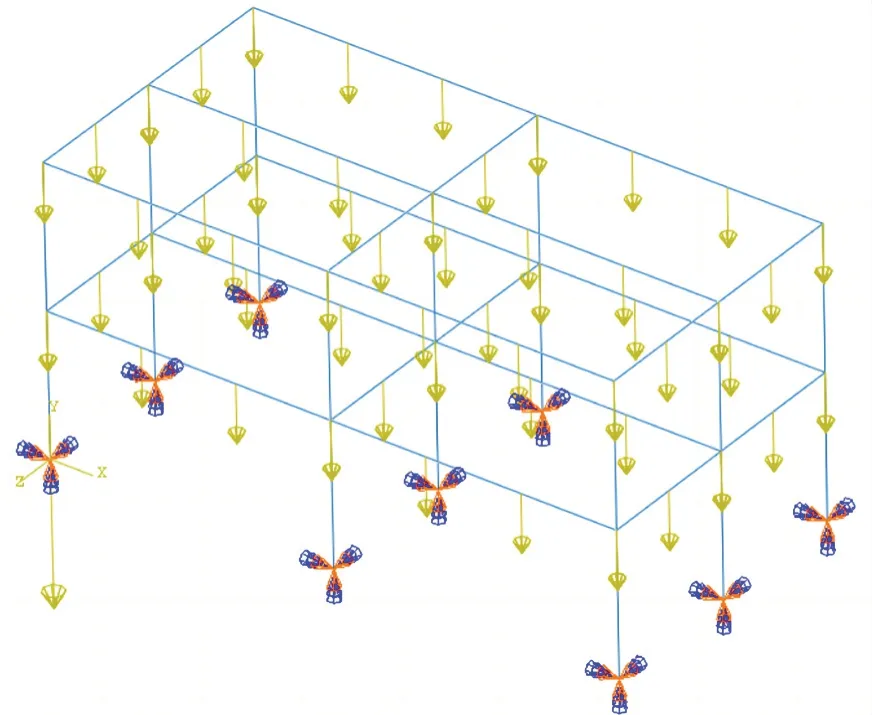
图5 有限元计算模型

3 结果分析

经过Abaqus 程序41 次优化计算，得到空间钢框架结构优化的最终结果。如表3、图6 所示，随着迭代次数的增加，模型构件的截面和目标函数不断减小，模型重量最终在第34 次计算后开始收敛，并于第40次计算完成迭代，优化后的结果钢材用料比原结构节约59.43%。从图6 可以看出，模型中钢梁变形最大处在跨中，这是因为模型只受竖向的均布荷载的缘故，在梁柱节点处出现应力集中现象，与优化前相比结构性能得以充分利用。

表3 模型总重量优化结果

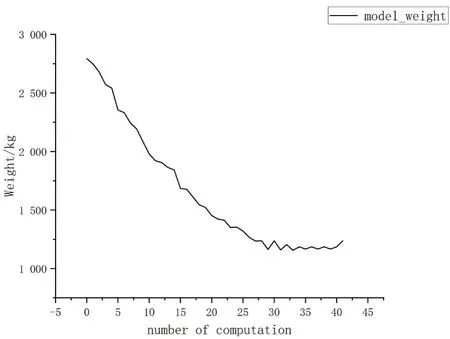
图6 模型总重量变化图（单位：kg）

一层、二层钢梁在优化过程中重量的变化如图7（a）~（b）所示。从中可以看出，部分构件（如beam1、11、13、24）基本在第八次计算结束后已经开始收敛，同时如表4、表5 所示，外侧纵梁的优化程度较低，这是因为该构件在原模型中就已经接近设计上的极限，留给优化的余地已经很小了。构件挠度随着构件截面减小增加，但最终仍满足规范l/400 的要求。从构件失效的原因来看，起主要控制作用的是挠度和稳定性，其中构件因为整体稳定性失效的次数更高，在设计中建议通过提高该构件受压翼缘的侧向稳定性来减少失效风险。

表4 一层钢梁优化过程中参数变化

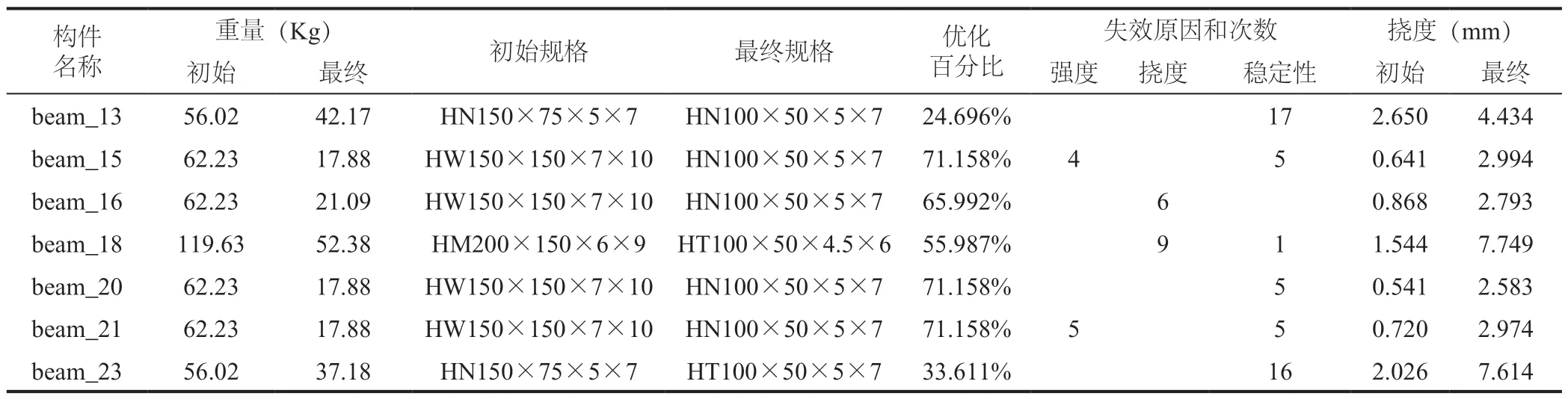
表5 二层钢梁优化过程中参数变化

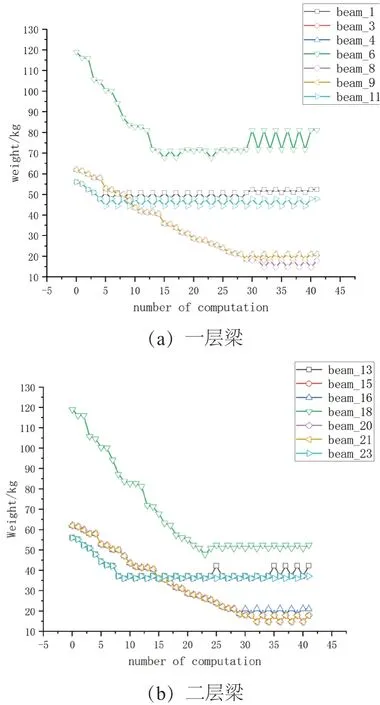
图7 钢梁重量变化图（单位：Kg）

模型中钢柱的重量曲线如图8（a）~（b）所示，在优化前期基本重叠，这是模型的荷载对称布置的原因。如表6、表7 所示，柱在原模型中的设计过于安全，经过优化后，钢柱重量普遍为原构件的55.483%~70.018%。钢结构的破坏形式中失稳破坏最为常见，从模型中钢柱的失效原因也可以看出平面外稳定性起关键控制作用。

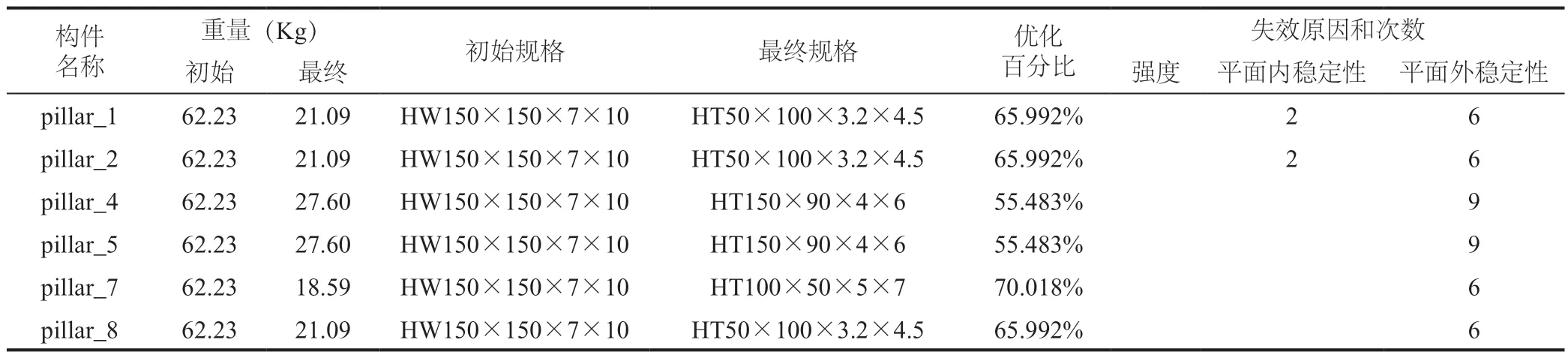
表6 一层钢柱优化过程中参数变化

表7 二层钢柱优化过程中参数变化

图8 钢柱重量变化图（单位：kg）

4 结论

本文利用有限元软件Abaqus 的计算模块以及其Python 语言接口，通过编写子程序实现Abaqus 二次开发，对空间钢框架离散优化设计，以结构可靠性为前提，利用计算机程序快捷、方便地完成了整个优化设计过程，得到了经济安全的最优设计结果。同时，本文分析了常见空间钢框架模型中钢梁和钢柱的失效原因，并给出了相应建议。本文的研究对实现钢结构性能化设计具有参考价值，也有一定的工程实际意义，从而推动钢结构设计的智能化、经济化。