基于多类型换流设备的受端电网耦合鲁棒阻尼控制策略

2024-03-26孙天一李保宏张英敏王腾鑫

电力自动化设备 2024年3期

孙天一，李保宏，江琴，张英敏，张敏，王腾鑫

（1.四川大学电气工程学院，四川成都 610065；2.国网山西省电力公司电力科学研究院，山西太原 030001）

0 引言

高电压等级、远距离、大容量的直流输电以及交直流系统的大规模互联将有效缓解我国能源与负荷中心呈逆向分布的问题，促进可再生能源的消纳。江苏省是华东地区的重要负荷中心，电能消耗大，但能源较为紧缺。目前，有包括800 kV 白鹤滩—江苏混合级联直流、500 kV 龙政直流和800 kV 锦苏直流等在内的多回直流输电线路馈入江苏电网。江苏受端电网直流落点密集，且多集中于负荷较重的苏州南部地区，使得部分线路面临过载的风险进一步增大。2017 年于苏州南部投运的500 kV 统一潮流控制器（unified power flow controller，UPFC）工程优化了苏州南部地区主要输电通道潮流，有效提升了江苏电网的区外受电能力［1］。

江苏电网是白鹤滩—江苏混合级联直流的受端电网，随着白鹤滩—江苏混合级联直流工程的投运，江苏电网区外来电比例不断增加，替代了受端电网的常规电源，江苏电网本地电源开机比例逐渐减少，降低了发电机与系统之间的联系电抗，电网“空心化”程度愈发明显，并且白鹤滩—江苏混合级联直流落点位于负荷中心苏州市，使负荷密集地区开机惯量逐渐减小，电网缺少中部惯量支撑，进而带来直流落点近区的动态稳定振荡阻尼比降低的问题，再加上UPFC 频繁调节线路潮流，使得江苏电网发生低频振荡的风险进一步升高。常规电力系统的低频振荡问题可以采用电力系统稳定器（power system stabilization，PSS）进行抑制，但白鹤滩—江苏混合级联直流的投运使江苏电网的系统特性进一步改变，振荡特性更加复杂，多种振荡模式相互耦合，PSS 难以实现更佳的抑制效果［2-3］，这使得附加阻尼控制器抑制振荡得到了广泛关注。由于白鹤滩—江苏混合级联直流逆变侧和江苏电网UPFC 中有不同的换流器，它们具有定功率控制能力，可以作为附加阻尼控制器的安装地点，因此，采取附加阻尼控制器是抑制江苏电网低频振荡问题的有力措施。目前对于电力系统附加阻尼控制方面的研究，较为成熟的分析方法有鲁棒控制［4-7］、最优控制［8-9］、自适应控制［10-11］和模糊控制［12-14］等。其中，鲁棒控制的应用最为普遍。文献［4］建立了含直流断路器的多端柔性直流输电系统小信号模型，利用模态分析法分析了影响系统稳定性的主要因素，并针对断路器系统导致的稳定性问题，设计了基于H∞混合灵敏度理论的阻尼控制器以改善系统的弱阻尼特性。文献［6］为应对风电出力不确定性，以大容量风电柔直送出、受端含常规机组的试验系统为研究对象，依托送端静止同步补偿器（static synchronous compensator，STATCOM）设计了基于H∞的鲁棒控制器以抑制次同步振荡。文献［7］提出了多工况综合留数指标来选择反馈信号及控制器安装地点，并采用混合H2／H∞方法设计控制器以抑制交直流混联电网的区间振荡。

由于江苏电网交直流输电设备多，各发电机地理位置较为分散，机组间往往存在多个振荡模式，现有的鲁棒阻尼控制器设计方法多为单输入单输出（single-input single-output，SISO）的形式，单一控制回路的鲁棒阻尼控制器反馈信号仅有1 个，在复杂电力系统或故障点距离控制器安装地点较远的情况下难以体现其鲁棒性。另外，现有的基于多个控制回路进行解耦设计的多输入多输出（multi-input multioutput，MIMO）控制器在电力系统规模比较大、电网间的联系较为紧密以及控制设备较多的情况下难以消除回路间的耦合，还有可能出现相对增益矩阵（relative gain array，RGA）方法难以找到合适的控制回路进行配对的情况，从而影响控制器的效果。

为进一步提高江苏电网的稳定裕度，增强江苏电网的故障应急支撑能力，本文利用江苏电网现有的苏州南部UPFC 和混合级联直流逆变侧模块化多电平换流器（modular multilevel converter，MMC）的定功率控制能力，无须通过对不同控制回路进行解耦，直接通过获取系统的状态空间方程设计MIMO耦合鲁棒阻尼控制器以抑制低频振荡。首先基于主模比指标为控制点选取合适的反馈信号，再利用总体最小二乘-旋转不变技术（total least squaresestimation on signal parameters via rotational invariance technique，TLS-ESPRIT）算法辨识系统降阶模型，最后基于混合H2／H∞鲁棒控制方法设计MIMO耦合鲁棒阻尼控制器。在白鹤滩—江苏混合级联直流与受端江苏电网的互联系统仿真中验证了该方法的有效性。

1 混合级联直流与UPFC模型及其控制策略

1.1 混合级联直流模型及控制策略

白鹤滩—江苏特高压混合级联直流单极拓扑结构如附录A 图A1 所示。每一个完整单极的整流侧均由2 组12 脉动LCC 串联而成，逆变侧均由1 组12脉动LCC 和MMC 并联组串联而成，MMC 并联组由3 个半桥型MMC 并联构成。混合级联直流中LCC的控制方式与常规直流基本相同，整流侧的2 组LCC 均采用定直流电流控制，并配置最小触发角控制作为后备控制，逆变侧LCC采用定直流电压控制，并配置定关断角控制和定电流控制作为后备控制。

逆变侧MMC 采用基于dq解耦的直接电流矢量控制，控制策略如图1 所示。图中：Vdc、Vac和Vdc_ref、Vac_ref分别为MMC 直流侧电压和交流侧电压及其指令值；P、Q和Pref、Qref分别为MMC 输出有功和无功功率及其指令值；us，d和us，q分别为d、q轴扰动变量；Vdiff，d_ref、Vdiff，q_ref分别为MMC 上下桥臂差模电压d、q轴分量指令值；Id、Iq及Id_ref、Iq_ref分别为内环电流控制器的输出值d、q轴分量及其指令值；ω为同步角速度；L=Lac+L0/2，Lac为换流变压器每相的等效电感，L0为桥臂电感；PI为比例积分控制器。MMC 系统级控制策略采用主从控制，有功类控制策略为1 台MMC 控制直流电压，其余MMC 控制有功功率，无功类控制策略为所有MMC控制无功功率［15-16］。

图1 换流器控制策略Fig.1 Control strategy of converter

1.2 UPFC模型及控制策略

苏州南部UPFC 工程位于苏州市500 kV 木渎变电站和梅里变电站之间，其结构如图2 所示，所采用的换流器为MMC。图中：U1、U2分别为木渎变电站、梅里变电站母线电压；Udc为直流电流。并联换流器与木渎500 kV 母线并联，2 个串联换流器分别串联在木渎—梅里双回线路上，并联侧与串联侧之间换流器通过直流母线背靠背连接。并联换流器采用定交流电压控制和定直流电压控制，以维持交流母线电压和直流母线电压恒定；串联换流器采用定有功功率控制和定无功功率控制，对所在线路潮流直接进行控制。

图2 苏州南部UPFC结构Fig.2 Structure of UPFC in southern Suzhou

2 MIMO系统混合H2／H∞鲁棒控制理论

2.1 控制器设计目标

混合H2／H∞鲁棒控制的系统结构见附录A 图A2。该系统的状态空间方程可描述为：

式中：x为系统状态变量；A为状态矩阵；B1为扰动增益矩阵；B2为控制输入矩阵；u为控制变量；y为系统输出；w为系统外部摄动；z2和z∞分别为与摄动w相对应的输出变量；C∞、D∞1和D∞2分别为与H∞指标相关的状态变量、扰动变量和控制变量系数矩阵；C2、D2分别为与H2指标相关的状态变量、控制变量系数矩阵；Dy1、Dy2分别为与w、u对应的直接传输矩阵；C为系统输出矩阵。

对于所描述的系统，要求设计的控制器应满足以下3个目标［17］：①闭环系统是渐近稳定的；②H∞性能，从w到z∞的闭环传递函数T∞（s）的H∞范数不超过给定的上界γ∞（γ∞＞0），使得系统对由w引起的扰动不确定性具有鲁棒稳定性；③H2性能，从w到z2的闭环传递函数T2（s）的H2范数不超过给定的上界γ2（γ2＞0），使系统性能达到最优。

2.2 控制器目标实现

1）区域极点配置。江苏电网本身结构复杂，必然存在模型以及扰动的不确定性，难以确保电网长期处于稳定运行状态。但只要将系统的闭环极点配置于图3 所示的复平面的区域D中，就可以保证系统是渐近稳定的，且具有一定的动态和稳态性能。图中：l0为极点配置区域范围至虚轴距离的最小值；θ为极点配置区域范围的相角最大值。

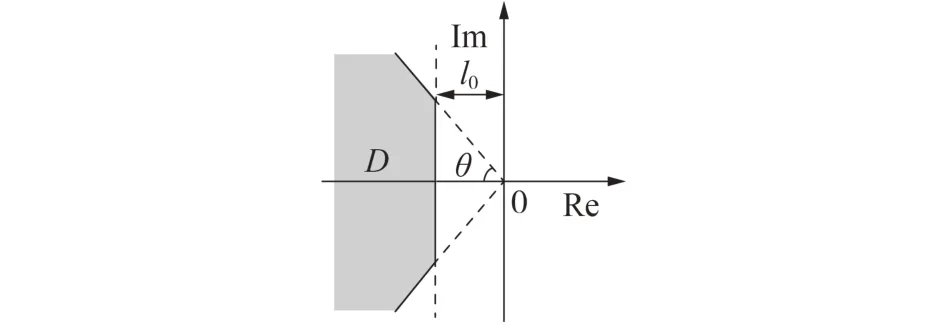
图3 极点配置区域Fig.3 Pole configuration area

要求系统闭环极点位于图3 给定区域内，用矩阵不等式描述为：

式中：C为复数域；L和M满足式（3）所示关系式。

对于电力系统低频振荡的抑制，应使闭环系统特征值位于阻尼比ζ＞cosθ的区域内，且闭环系统的特征值离虚轴不能太近，以使故障后系统回到稳定的调节时间更短［7］。区域极点配置问题可使用MATLAB中的LMI工具箱求解。

2）混合H2／H∞控制。H∞性能指标反映了系统对干扰的抑制效果，从w到z∞的闭环传递函数T∞(s)的H∞范数‖T∞(s)‖∞定义为：

式中：‖T∞(s)‖∞表示同步角速度ω响应的最大奇异值σmax（·）的峰值pk｛·｝，从时域角度来看，其是对任意频率正弦输入最差情况下的稳态增益。由有界实引理，满足2.1 节中控制器设计目标式（1）的充要条件为当且仅当存在对称正定阵P∞，使式（5）成立。

H2性能指标反映了系统在受到白噪声干扰时相应输出的渐近变化。从w到z2的闭环传递函数T2(s)的H2范数‖T2(s)‖2定义为：

式中：t（r·）代表矩阵的迹；(T2*(jω))T为T2(jω)的共轭转置。由式（6）可知，T2(s)的H2范数等于系统脉冲响应的输出能量的均方根值。满足2.1 节中控制器设计目标式（3）的充要条件为当且仅当存在对称正定阵P2和Q，使式（7）—（9）成立。

式中：I为单位阵。混合H2／H∞控制问题是一个多目标控制问题，应使性能指标J满足：

式中：α为鲁棒性能权重系数，β为控制代价权重系数，二者之和为1，可根据控制器设计效果将α和β设为不同数值。对于固定的权重，所设计的控制器应使J最小。

3 模型辨识与反馈信号选择

TLS-ESPRIT 算法既可以对仿真数据进行分析，又可以进行系统辨识。与Prony方法相比，该算法的抗干扰、抗噪能力更强，可有效恢复谐波并求取信号的衰减参数，是进行电力系统低频振荡模式辨识最常用的方法之一。TLS-ESPRIT 算法的总体思路是利用采样数据构建Hankel 矩阵H，再通过奇异值方法将矩阵H分解为信号空间和噪声空间，进而求得信号的旋转算子，通过旋转算子可进一步得到各模态的振荡频率、衰减因子等特征参数［18］。

设计控制器时，为使控制器对系统弱阻尼具有良好的阻尼作用，且对其他模式的耦合作用小，常用主模比指标衡量单位控制输出量的阻尼效果［7］，相比留数法，该指标可以使不同种类的信号之间进行直接比较。主模比的计算公式为：

式中：|cϕi|为反馈信号Δy对于主导振荡模式的可观性；|zi(0) |为扰动后零时刻主导振荡模式的振幅；|cϕk|为反馈信号Δy对于第k个振荡模式的可观性；|zk(0) |为扰动后零时刻第k个振荡模式的振值；n为振荡模式总数。

本文通过在系统稳态时对其施加小扰动激励，利用TLS-ESPRIT 算法识别出系统存在的振荡模式，在备选信号中选取主模比指标最大信号作为控制器设计的反馈信号，并再次利用TLS-ESPRIT 算法辨识系统MIMO模型，然后基于系统状态空间模型的最小化实现原理对系统进行降阶，消除传递函数中的零极点对，得到系统降阶传递函数。最后利用H2／H∞方法设计耦合鲁棒阻尼控制器，将其加在对应换流器的控制回路中，以提高系统弱阻尼振荡模式的阻尼。

4 算例分析

4.1 江苏电网结构

在江苏电网2023 年夏高规划数据中，白鹤滩—江苏混合级联直流双极共输送功率8 000 MW，逆变站位于江苏省常熟市，其受端近区500 kV 主体网架结构如附录A 图A3所示。其中，逆变侧LCC 送出功率4 000 MW，其出线分别接入常熟南和斗山。MMC并联组共送出功率4 000 MW，其中MMC1出线分别接入常熟北和张家港，MMC2出线接入木渎，MMC3出线接入玉山。MMC1采用定直流电压控制，直流电压指令值为400 kV。MMC2和MMC3采用定功率控制，各送出功率1 334 MW。苏州南部UPFC 安装在木渎—梅里线路靠近木渎侧的位置。

鉴于系统规模庞大，采用电磁暂态仿真虽仿真精确，但建模复杂、计算速度慢；机电暂态仿真基于系统稳态模型或准稳态模型，适合大规模交直流互联系统仿真，但难以准确反映电力电子设备主电路、控制策略、响应速度等特性［19］。本文基于电力系统全数字仿真（advanced digital power system simulation，ADPSS）程序进行机电-电磁混合仿真，搭建双极混合级联直流和UPFC 的详细电磁模型，并对受端江苏电网进行机电暂态建模，机电暂态模型中，发电机、220 kV及以上电压等级线路、变压器等参数与实际工程一致，110 kV 及以下电压等级电网等效为负荷，避免了电网的大范围等值简化，同时提高了仿真规模和准确性。

4.2 基于主模比指标的反馈信号选择

可供选择的反馈信号有很多，为便于分析，本文选取江苏电网部分电厂发电机转速差进行主模比指标计算。扰动选取惠泉、石牌、车坊等江苏电网500 kV 关键母线三相短路故障，故障持续时间为0.1 s，主模比指标的平均值计算结果如表1所示。

表1 主模比计算结果Table 1 Calculative results of dominant mode ratio

从表1 可以看出，碧溪—华能苏州电厂转速差信号Δω1和华能苏州—利港二厂转速差信号Δω2的平均主模比指标最大，二者可作为反馈信号，即耦合鲁棒阻尼控制器的输入信号。由于所选信号均为广域测量信号，本文采用2 阶Pade 多项式逼近方法来模拟控制回路产生的时滞，其表达式为：

式中：τ为时滞，取40 ms。通过TLS-ESPRIT 算法辨识得到系统存在的振荡模式见表2。由表可知，系统的弱阻尼振荡模式有1.535 6 Hz和0.913 2 Hz这2个，其中1.535 6 Hz 的阻尼比接近于0，控制器的设计目标是将特征值左移，以提高该振荡模式的阻尼比。

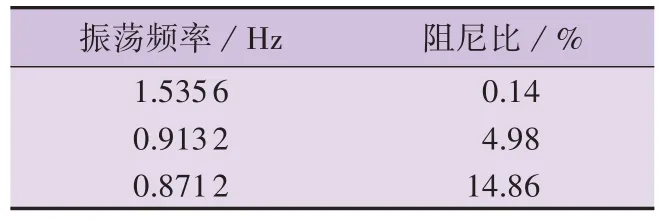
表2 系统的振荡模式Table 2 Oscillation modes of system

4.3 MIMO系统模型辨识

系统开环模型的输入输出关系可以表示为：

式中：u1(s)和u2(s)为柔性输电设备的控制输入；y1(s) 和y2(s) 为系统的输出；G11(s) 为从u1(s) 到y1(s)的传递函数；G12(s)为从u2(s)到y1(s)的传递函数；G21(s)为从u1(s)到y2(s)的传递函数；G22(s)为从u2(s)到y2(s)的传递函数。本文分别选取UPFC 和MMC3定有功功率控制指令值作为系统的输入，机组转速差信号Δω1和Δω2作为系统的输出。

由式（13）可知，令u2(s)=0，在不改变原系统线性化条件的情况下，在输入u1(s)处施加小扰动激励并进行TLS-ESPRIT 辨识，可以分别得到G11(s)和G21(s)。类似地，G12(s)和G22(s)均可通过在u2(s)处施加扰动并辨识得到。降阶传递函数辨识结果见附录A 式（A1）。式中，4 个传递函数构成的G(s)为18 阶矩阵，系统降阶前、后的Bode 图如附录A 图A4所示。由图可见，降阶前、后系统Bode 图保持吻合，虽然辨识得到的模型阶数远低于实际系统，但其仍可以全面反映系统的振荡信息。

4.4 耦合鲁棒阻尼控制器设计

在设计控制器时，为了使H2和H∞性能指标满足要求，需要对系统模型选择合适的权函数。一般地，W1(s)为高通滤波器，W2(s)为低通滤波器，W3(s)可设置为一个较小的常数，且所选权函数的阶数不宜过高。对于权函数的选取没有固定的方法，经反复试验，选取权函数为：

给定权函数后，使用MATLAB 中的鲁棒工具箱，令式（10）中的权重系数α=β= 0.5，设定特征值的实部小于-0.75，可求得图3 中区域D对应的矩阵L。配置不同的阻尼比，使用hinfmix 函数求解出无γ2和γ∞限制的控制器。系统输入、输出与控制器传递函数阵之间的关系可表示为：

式中：K11(s)、K12(s)、K21(s)和K22(s)分别为从y1(s)到u1(s)、从y2(s)到u1(s)、从y1(s)到u2(s)和从y2(s)到u2(s)的控制器。

为了获取控制器对于不同阻尼比参数的敏感性，同时使所设计的控制器效果最佳，在辨识出系统低阶模型的基础上，在输入u1(s)处施加幅值为1 的阶跃，对比系统在无控制器以及在配置不同阻尼比的控制器情况下的输出y1(s)和y2(s)的阶跃响应见附录A 图A5。由图可知，阻尼比参数是影响控制器效果的关键因素。在分别配置阻尼比参数大于10 %、12.5 % 和15 % 的情况下，所设计的控制器均对于原线性化系统施加阶跃扰动后发生的振荡具有抑制效果，且随着阻尼比的增大，控制器的抑制效果更显著，但阻尼比不能继续增大，否则将无法求解出控制器的传递函数。故设阻尼比大于15%，并求得区域D对应的矩阵M，据此求解对应的控制器传递函数。

所设计的每个SISO 控制器在考虑权函数的情况下均为22 阶，考虑控制器实现的难易程度，利用平衡截断法进行降阶，控制器降阶后的表达式见附录A 式（A2）。降阶前、后控制器Bode 图如附录A 图A6所示，在所关心的低频段内，降阶前、后Bode图均保持一致，满足要求。

为了验证耦合鲁棒阻尼控制器的性能，将其与实际工程中广泛采用的经典超前-滞后控制器进行对比，控制器传递函数G表达式为：

式中：K为增益；T1、T2为时间常数。控制器参数通过极点配置得到，其中，加入UPFC 定有功功率控制回路的控制器参数为K=1.2、T1=0.2 s、T2=4 s；加入MMC3定有功功率控制回路的控制器参数为K=0.75、T1=0.6 s、T2=4 s。仿真设置控制器输出限幅为±0.5。

4.5 仿真验证

耦合鲁棒阻尼控制器结构如图4 所示，将其和传统控制器分别加入系统的对应控制通道中，在ADPSS 混合仿真程序中施加不同扰动进行对比验证。为避免扰动较大从而引起换流设备所控制线路的功率变化过大，在控制器输出后配置了限幅环节。图4 中所涉及的主要控制参数设置如附录A 表A1所示。

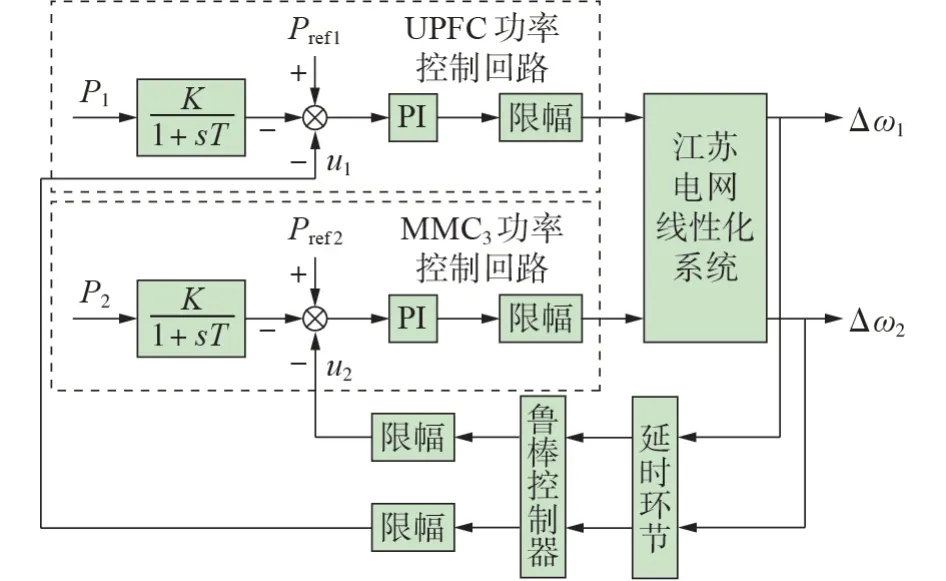
图4 耦合鲁棒阻尼控制器结构Fig.4 Structure of coupled robust damping controller

1）扰动1。1 s 时，石牌母线发生单相接地短路故障，故障持续时间为0.1 s，对无控制器、投入耦合鲁棒阻尼控制器和传统控制器情况下的反馈信号Δω1和Δω2响应进行对比，控制器的抑制效果对比如图5所示。图中：Δω1和Δω2均为标幺值，后同。

图5 扰动1情况下系统的动态响应Fig.5 System dynamic response for Disturbance 1

2）扰动2。1 s 时，谏壁电厂1 台发电机断开，该情况下Δω1和Δω2振荡模态的抑制效果对比见图6。

图6 扰动2情况下系统的动态响应Fig.6 System dynamic response for Disturbance 2

由图5、6 可知，对于小扰动，耦合鲁棒阻尼控制器和传统控制器均能抑制低频振荡，但前者的恢复特性更好，相比于传统控制器具有更佳的抑制效果。

3）扰动3。1 s时，太仓母线发生三相短路故障，故障持续时间为0.1 s。该情况下Δω1和Δω2振荡模态的抑制效果对比如图7所示。

图7 扰动3情况下系统的动态响应Fig.7 System dynamic response for Disturbance 3

由图7 可知，相较于扰动1 和扰动2，当系统发生更为严重的三相短路故障时，在振荡前期，传统超前-滞后控制器可以抑制系统的低频振荡，而在故障消失后的较长一段时间内，传统控制并不能完全使系统回到稳定运行状态，并存在引发欠阻尼振荡的可能，这是因为2 个传统控制器基于系统线性化模型设计，大干扰下系统的线性化模型发生变化，传统控制对于模型发生变化后的系统不能发挥作用。而基于混合H2／H∞方法的耦合鲁棒阻尼控制器在设计时充分考虑了鲁棒性，该控制器对系统模型变化不敏感，在系统发生各种扰动时均能表现出良好的控制效果和抗干扰性能，可确保系统在多种工况下的稳定运行。为了更直观地说明耦合鲁棒阻尼控制器所发挥的作用，附录A 图A7 给出了在以上3 种扰动情况下耦合鲁棒阻尼控制器的输出。