A Tri-mode of Mock-Walker Cells
2024-03-26HanQINJiNIEandZhiyongMENG
Han QIN, Ji NIE*,2, and Zhiyong MENG,2
1Laboratory for Climate and Ocean-Atmosphere Studies, Department of Atmospheric and Oceanic Sciences,School of Physics, Peking University, Beijing 100871, China
2China Meteorological Administration Tornado Key Laboratory, Foshan 528061, China
ABSTRACT This work uses cloud-resolving simulations to study mock-Walker cells driven by a specified sea surface temperature(SST).The associated precipitation in the mock-Walker cells exhibits three different modes, including a single peak of precipitation over the SST maximum (mode 1), symmetric double peaks of precipitation straddling the SST maximum(mode 2), and a single peak of precipitation on one side of the SST maximum (mode 3).The three modes are caused by three distinct convective activity center migration traits.Analyses indicate that the virtual effect of water vapor plays an important role in differentiating the three modes.When the SST gradient is large, the virtual effect may be strong enough to overcome the temperature effect, generating a low-level low-pressure anomaly below the ascending branch of the Walker cell off the center.The results here highlight the importance of the virtual effect of water vapor and its interaction with convection and large-scale circulation in the Walker circulation.
Key words: Walker circulation, cloud-resolving simulation, virtual effect
1.Introduction
A common and useful way to understand the tropical large-scale dynamics is to consider a circulation driven by prescribed sea surface temperature (SST).There is a long history of attempting to explain the tropical mean circulation and precipitation by the distribution of SST [e.g., as reviewed in Sobel (2007)], and previous studies can be classified into three groups of ideas.The first idea notes that, due to the weak temperature gradient (WTG) in the free tropical troposphere, air columns over higher SST should be more convectively unstable and have greater rainfall (e.g., Sobel et al.,2001; Chiang and Sobel, 2002; Bretherton and Sobel,2002).The second idea, represented by Lindzen and Nigam(1987), argues that the SST gradient drives low-level winds,and its associated convergence leads to precipitation.The first and second ideas predict precipitation maxima over SST maxima and regions of large SST gradient, respectively.The observational relationship between SST and climatological rainfall suggests a mixture of the above two situations.Thus, the third idea combines the above two ideas by including a deep and a shallow mode of convection (e.g.,Neelin and Held, 1987; Back and Bretherton, 2009a, b).Despite previous advances in linking tropical mean circulation and SST, the problem remains unresolved.For example, the models in many previous studies are still diagnostic models with posteriori parameters.The double intertropical convergence zone (double-ITCZ) bias is still a persistent problem in many climate models (Samanta et al., 2019; Fiedler et al., 2020; Tian and Dong, 2020).
The complexity of tropical dynamics largely comes from interactions between large-scale circulation and smallscale convection (Emanuel et al., 1994; Raymond, 1994;Singh and Neogi, 2022).A useful prototype for studying such a problem is the mock-Walker circulation (or cell): a two-dimensional non-rotating circulation forced by specified zonally varying SST (Bretherton et al., 2006).The mock-Walker circulation is an idealized simplification of the tropical Walker circulation, which is the equatorial overturning circulation cell ascending over the west Pacific warm pool and descending over the east Pacific cold pool (Bjerknes, 1969;Dong and Lu, 2013; Ma and Zhou, 2016).The Walker cell plays an important role in tropical and global climate.For example, the interannual variability of the Walker cell is the atmospheric component of the El Niño-Southern Oscillation(Bjerknes, 1969; Williams and Funk, 2011; Bayr et al.,2014), and the changes in the Walker cell under global warming greatly impact regional climate in the tropics (Kousky et al., 1984; McGregor et al., 2014).
The mock-Walker cell has been investigated by several studies.Liu and Moncrieff (2008) found that boundary layer processes of friction and wind-induced surface flux variability play an important role in determining the precipitation distribution in mock-Walker cells.Kuang (2012) found that increasing the domain size strengthens the mock-Walker cell and alters its vertical structure.With uniform increases of SST, which mimic global warming, the precipitation of the mock-Walker cell increases and the width of the precipitation band narrows (Bretherton et al., 2006; Wofsy and Kuang, 2012).These studies mostly used high-resolution cloud-resolving models to better represent the small-scale convection and its interaction with large-scale dynamics.An interesting observation in these studies, yet has not been explored, is the behavior of the precipitation distribution.In some simulations, there is one precipitation peak over the SST maximum, while in other simulations with different settings, precipitation shows a double-peak distribution (Chao and Chen, 2004; Bretherton et al., 2006; Bellon and Sobel,2010; Gastineau et al., 2011; Möbis and Stevens, 2012; Harrop and Hartmann, 2016; Silvers and Robinson, 2021).This behavior is analogous to the single versus double ITCZ problem in aqua-planet simulations (e.g., Chao and Chen, 2004;Voigt and Shaw, 2015), even though there is no Coriolis force in the mock-Walker cell.
In this study, we explore the characteristics of mock-Walker cells, particularly the associated precipitation distribution, over a variety of SST and domain sizes, to achieve a better understanding of the key dynamics of the mock-Walker cells.In section 2, we briefly describe the numerical model and experimental design.In section 3, we show an unreported, third type of mock-Walker cell with a single precipitation peak at one flank of the SST maximum.Together with the single- and double-peak precipitation shown in previous studies, it consists of a tri-mode of mock-Walker cells.In section 4, we elaborate the key mechanism of the tri-mode of mock-Walker cells, the virtual effect of water vapor.Conclusions and some further discussion are provided in section 5.
2.Numerical model and experimental design
The model used here is the System of Atmospheric Modeling (Khairoutdinov and Randall, 2003), version 6.10.4.There are six water species in the microphysics scheme:water vapor, cloud liquid, cloud ice, snow, rain, and graupel.The interactive radiation scheme is from the National Center for Atmospheric Research Community Climate Model (Kiehl et al., 1998).The height of the model top is 27 km, with 64 vertical levels.The vertical grid spacing gradually increases from 37.5 m at the surface to 500 m above the middle troposphere.The SST is prescribed, and the surface fluxes are interactively computed using Monin-Obukhov similarity theory.The solar insolation is similar to that in Bretherton et al.(2006), which is a temporally and horizontally uniform insolation of 413.6 W m-2.The simulation domain is a horizontally double-periodic narrow channel in which the meridional extent of the domain (64 km) is much smaller than the zonal extent (Table 1).In all the experiments, the horizontal resolution is 4 km.The Coriolis parameter is equal to zero.The initial profiles for temperature and water vapor are taken from the steady state of radiative convective equilibrium simulation under the same SST.The initial vertical profiles of winds are set to zero.
The circulation is forced with a zonally Gaussian-distributed SST in all the cases:
In Eq.(1), µ is half of the zonal domain length, so the SST peaks at the center.δ and σ set the amplitude and halfwidth of the SST distribution, respectively.The SST is uniform in the y direction.To examine the behavior of mock-Walker cells in different parameter regimes, we carried out three groups of experiments with different zonal domain sizes, δ , and σ (Table 1).Cases in the first group of experiments (named S) are in a small domain (1024 km in the x direction) with σ =128 km.Each case has a different δ varying from 1 K to 16 K.The second group (named L) has both a zonal domain and σ that are four times larger than those of the first group.It includes five cases with δ varying from 2 K to 14 K.The third group (named LW) is the same as the second group, except the half-width of the Gaussian distribution is 1.5 times wider ( σ =768 km).Each case is named as the group name followed by its δ.For example,case “LW2” refers to the case in group LW with δ=2 K.All cases are run until a statistical equilibrium state (300 to 1000 days) is reached, and the first 100 days are discardedas spin-up.In the following analyses, the variables are averaged in the meridional direction.
3.The tri-mode of mock-Walker cells
The mean precipitation shows three different modes of the mock-Walker cells (Fig.1).In group S (Fig.1a), there is a single precipitation peak over the SST maximum when δ ≤8 K, and there are two peaks of rainfall over the two sides of the SST maximum when 10 K ≤δ ≤16 K.In group L (Fig.1b), there is a single precipitation peak over the SST maximum when δ ≤6 K ; however, as δ ≥10 K, the precipitation peak is off-center.The cases in group LW (Fig.1c) are similar to those in group L, but the transition from the central peak to the off-center peak occurs at a smaller δ(4 K).The single precipitation peak over the SST maximum when the SST gradient is weak is named mode 1, which is consistent with the WTG argument.A large SST gradient leads to the double-peak precipitation (named mode 2) in the small domain simulations (group S) and the off-center single-peak precipitation (named mode 3) in the large domain simulations(group L and LW).The double-peak precipitation over the large SST gradient region (i.e., the flank of SST maximum)is consistent with the Lindzen and Nigam model.The off-center-peak precipitation in the Walker cell is a new mode that has not been reported before.This is intriguing, since asymmetric circulation develops under a symmetric setup.In addition, within each group, as SST differences increase, the convective regions tend to become narrower and stronger, consistent with Bretherton and Sobel (2002).
The circulation of mock-Walker cells also shows a trimode corresponding to the precipitation (Fig.2).In the following analyses, we use one case for each mode as examples; other cases show qualitatively similar results.For mode 1 (Fig.2a), the rising branch of the Walker cell is strongest, and the associated relative humidity is highest at the domain center.The maximum of upper-tropospheric cloud condensate at the center indicates strong deep convection associated with the ascending air of the Walker cell.For mode 2 (Fig.2b), the maximum of ascending air, relative humidity, and cloud condensate are strongest at the flank of the domain center.For mode 3 (Fig.2c), the Walker cell is asymmetric.The rising branch and the associated deep convection locate on one side of the domain center.
The Hovmöller plots of precipitation clearly show the different characteristics of the three modes (Fig.3).The precipitation oscillates around the domain center, representing a propagating convectively coupled gravity wave (e.g.,Kuang, 2012).In mode 1 (Fig.3a), since the SST gradient is relatively weak, the convectively coupled gravity wave can propagate far away from the center.The precipitation rate is stronger over the higher SST regions; thus, the time-averaged precipitation shows a relatively flat distribution with the peak at the center.In mode 2 (Fig.3b), the large SST gradient confines the precipitation to be close to the domain center.The rainfall band traverses through the domain center rapidly, while staying at the flank for a longer time period.As a result, the time-mean precipitation shows double peaks.The distribution of precipitation reflects the duration that convection stays.In mode 3 (Fig.3c), the rainfall band persistently stays at one side off the center.Occasionally, it migrates to the other side, then moves back shortly after, leading to an off-center time-average precipitation peak at that moment.In some cases, we also observe situations where the rainfall band migrates to the other side and stays for a long time, which may lead to double-peak precipitation if averaging over a certain time period.However, this situation is also mode 3, since it is significantly different from the periodic oscillating rain belt in mode 2.To test the robustness of mode 3, we carried out three ensemble runs for the LW6 case with different random initial perturbations.The resulting Walker cells were all in mode 3.However, for the mode 3 cases, whether the precipitation peak locates at the left or right side of the center is random, depending on the initial conditions.

Fig.1.Zonal distribution of the time-mean precipitation of cases in experiment group (a) S, (b) L, and (c) LW.

Fig.2.The relative humidity, stream function and non-precipitating condensate of case (a) L2, (b) S14 and (c)LW14.The black solid/dashed contours show the positive/negative value of mass stream function, with black bold lines for zero values.The contour interval is 300 kg m-1 s-1 for group S and 600 kg m-1 s-1 for the remaining cases.Color shading denotes relative humidity.The white contours denote non-precipitating condensate, with contour levels of 0.01, 0.03, 0.05, 0.2, and 0.5 g kg-1.White dashed lines, denoting the domain center, are shown for reference.

Fig.3.Hovmöller plots of precipitation for three representative cases.The black lines show the domain centers,which are also the locations of SST maxima.
Based on the above observations, we can put forward the following conjecture.When the SST gradient is weak,the convective activity is mainly controlled by instability due to SST following the WTG argument (mode 1).When the SST gradient is large, deep convection preferentially stays in the region of large SST gradient (this state is called the off-center state).The off-center state is a common feature of mode 2 and mode 3.The difference is whether the off-center state can be sustained.In mode 3, the off-center state can be self-sustained, leading to an asymmetric Walker cell.In mode 2, the off-center state cannot be self-sustained, and the rainfall band oscillates between the two sides of the center, leading to two mean precipitation peaks.In the following section, we illustrate the basic characteristic of the off-center state and examine its sustaining mechanism.
4.Dynamics of the off-center state
To examine the off-center state, an objective and quantitative definition is needed.Using the S16 case as an example(Fig.4), we treat the time period when the distance between the precipitation centroids (magenta triangles) and the domain center is greater than a threshold (the black dashed lines) as the off-center state.The distance threshold is chosen dynamically for each case so that the time period of the leftside off-center state, right-side off-center state, and the rest(i.e., the at-center state) each occupies one-third of the total time period.As seen in Fig.4, this method of separation works well.However, for the cases of mode 3 (e.g., Fig.3c),since precipitation is at one side for most of the time, the threshold is adjusted so that the time period of the at-center state occupies one-fifth of the total time period.Our results are not sensitive to reasonable perturbations of the choice of the threshold.The at-center states of all cases are similar;the precipitation maximum, the rising branch of the Walker cell, and the minimum of surface pressure are all at the domain center.We mainly focus on the off-center state.

Fig.4.A schematic for defining the off-center state.The Hovmöller plot of precipitation for case S16 is superposed with magenta tringles that denote precipitation centroids at each time step.The grey zone with black dashed lines as the margins indicates the middle zone, outside which is the region of the off-center state.
The differences between the three modes of the mock-Walker cell may be illustrated by considering the moisture budget of the off-center state.Figure 5 shows the domainmean surface evaporation (i.e., latent heat flux) and precipitation of all cases at the off-center state.For the cases of mode 1 (red markers in Fig.5), the evaporation is greater than precipitation; thus, atmospheric moisture is charged during the off-center state and discharged during the at-center state.For the cases of mode 2 (blue markers in Fig.5), the situation is the opposite.Precipitation is stronger than evaporation during the off-center state, indicating that the off-center state is not sustainable.For mode 3 (green markers in Fig.5), the evaporation closely balances precipitation and thus the off-center state is sustainable as an equilibrium state.
Figure 6 shows the composites of anomalous pressure of the off-center state.Here, anomalies refer to removing horizontal means.We only show the results of the off-center state when precipitation peaks at the left-hand side; the results of the right-side off-center state are flipped using mirror transformation to increase the signal-to-noise ratio.At the off-center state, the low-level low-pressure center is at the domain center for mode 1 and mode 2.However, for mode 3, the low-level low-pressure center co-locates with the rising branch of the Walker cell off the center.The lowlevel winds flow toward the low-level low-pressure center,converge and ascend there, leading to large precipitation.The co-location between the pressure anomalies and precipitation is a fundamental feature of mode 3.It indicates that the off-center Walker cell may be maintained as a quasi-steady state.For mode 1 and mode 2, when the precipitation is off the center, its low-level pressure minimum is still at the center.Thus, this state is not sustainable and the rising branch of the Walker cell will migrate toward the domain center.
But what causes the off-center low-level low-pressure center in mode 3? The reason can be answered by examining the planetary boundary layer (PBL) thermodynamic variables(Fig.6).Due to the lack of the Coriolis effect, the horizontal pressure gradients are very weak above the PBL (Fig.6).The surface pressure distribution can be calculated by the pressure lapse rate in the PBL, which is determined by the air density.Mathematically, it can be written as

Fig.5.Scatterplot of time- and domain-averaged latent heat flux and precipitation for all cases under the off-center state.Cases of mode 1, mode 2 and mode 3 are denoted with red,blue and green markers, respectively.Cases in the three experimental groups are denoted with triangles, squares and circles, respectively.The sizes of markers indicate the SST difference ( δ) of each case.The black line is the one-to-one line for reference.
wherePsandPTBLare the pressure at the surface and top of the boundary layer, respectively;gis gravitational acceleration; andRis the ideal gas constant.In Eq.(2), we use the virtual temperature,Tv=T(1+0.608q-qc), to calculate the air density, since it depends on both temperature (T; units:K) and moisture (q; units: kg kg-1).qcstands for non-precipitating condensate and its influence is negligible.An air column with higher (lower)Tvin the PBL has lower (higher) surface pressure.
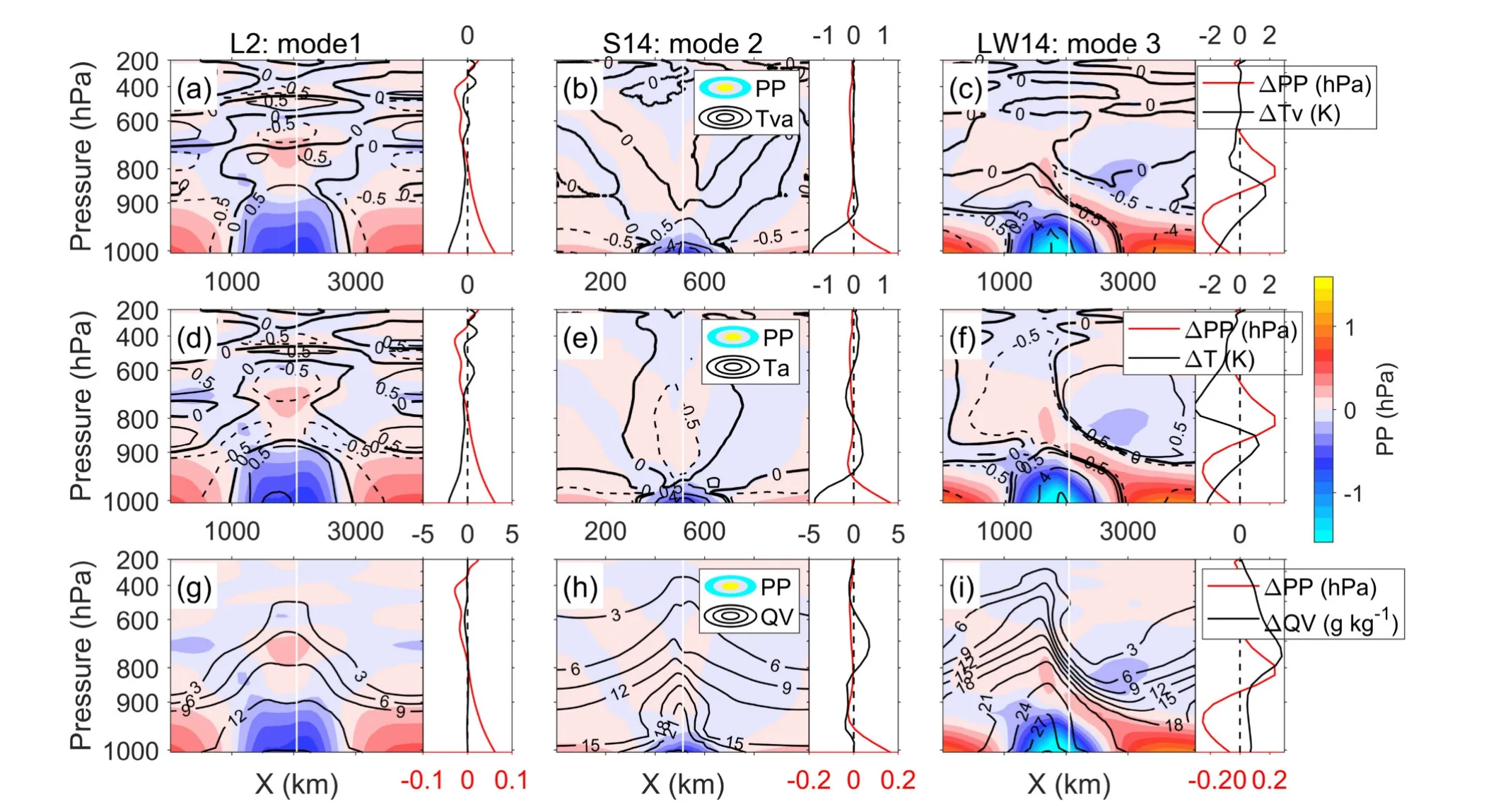
Fig.6.The composite off-center state.Each column is for case L2, S14, and LW14, for demonstration.In each row, the black contours are for virtual temperature anomalies, temperature anomalies, and moisture, respectively.In all panels, the color shading shows the pressure anomalies.The vertical lines on the right of each panel show the differences of variables between the ascending branch average and the central profile (former minus the latter).In the panels of profiles, the bottom axes are for pressure differences (red lines), while the top axes are for other variables (black lines).
The argument of Eq.(2) is confirmed by the distribution ofTvanomalies in Fig.6 (first row).The PBL pressure anomalies are closely correlated withTvanomalies.In mode 1 and 2, the PBLTvis strongest at the center, while for mode 3, the PBLTvis strongest off the center.Tvis determined by bothTandq.The PBLTis strongly constrained by SST, and it is strongest at the center for all the cases (second row of Fig.6).However,qclosely follows the ascending branch of Walker cells and has a maximum off the center for all the cases under the off-center state (third row of Fig.6).Moreover, as the SST gradient increases, the anomalousqbecomes larger.At the same time, the diabatic heating associated with the anomalous q also provides positive feedback for the vertical motion at the ascending the branch of the Walker cells.In mode 3, the anomalousqat the ascending branch is large enough so that its effect on air density (the virtual effect of water vapor) dominates.As a result, the surface low-pressure center locates under the rising branch of the off-center Walker cell instead of at the domain center over the SST peak.
The adjustment of the Walker cell and convection to an off-center area is sustainable since the water vapor anomaly generated is large enough.This virtual effect also explains why precipitation in Group LW switches to mode 3 ata smaller SST gradient than Group L.The σ is larger in Group LW, leading to a smaller SST gradient around the domain center and warmer average SST.Within the same group of cases (Group L and LW), the SST gradient drives the transition to mode 3.When comparing different groups,the average SST should also be considered.Warmer SST generates more water vapor, which indicates a stronger virtual effect.
We can quantitatively decompose the contribution of temperature and moisture on the PBL pressure anomalies to better demonstrate their competing effects.We integrate Eq.(2)downward from a free tropospheric level (700 hPa), and the conclusions are unaffected if we start from a different free tropospheric level.To evaluate the contribution of temperature to PBL pressure anomalies, we calculate theTvwith the horizontally averagedq, and then integrate Eq.(2) downward to the surface level.Similarly, the contribution of moisture is calculated by using horizontally averagedT.The results show that temperature anomalies generate PBL high-pressure anomalies at the center compared with the ascending branch(profiles in the first row of Fig.7), consistent with the distribution of PBLT(second row of Fig.6).On the other hand,the moisture anomalies generate PBL low-pressure anomalies off the center (second row of Fig.7), consistent with the distribution of PBLq(third row of Fig.6).By comparing each column in Fig.7, it is noticeable that for mode 1 and mode 2, the contribution of temperature anomalies dominates,while for mode 3 the virtual effect dominates.Thus, this analysis confirms the key role of virtual effects in the three modes of mock-Walker cells.The schematic in Fig.8 summarizes the key features and processes of the tri-mode of the mock-Walker cells.

Fig.7.Color shading in all panels shows the pressure perturbation reconstructed using the deviated field of temperature (first row) and specific humidity (second row).The three columns are for L2, S14 and LW14,respectively.Adjacent to the contours are the profile differences between the average ascending branch and central profile of the reconstructed pressure.

Fig.8.Schematic of the three modes of precipitation.The red shading denotes warm anomalies, the blue shading denotes moist anomalies, and LPC denotes the surface low-pressure center.
Lastly, we performed two series of additional simulations to test the sensitivity of our results to model resolution and background SST, respectively.In the first test, we repeated a couple of cases with doubled horizontal resolution (i.e.,grid spacing of 2 km).The cases were selected around the transition points in the original cases.The results (Figs.9ac) show three modes of precipitation distribution, similar with that in Fig.1.In the second test, we repeated cases in Group L but with the background SST increased from 298 K [Eq.(1)] to 300 K.The results (Fig.9d) also show a transition from mode 1 to mode 3 when δ ≥6 K, qualitatively similar with the results in Fig.1.Those sensitivity tests indicate that the transition point may depend on the background SST or model resolution, but the tri-mode characteristic of the mock-Walker cells is robust.
5.Discussion and conclusions
This study examined the mock-Walker cells driven by prescribed Gaussian SST using cloud-resolving simulations.With different amplitudes and widths of SST anomalies and domain sizes, the mock-Walker cells and associated precipitation show three different modes; namely, a single precipitation peak over the SST maximum (mode 1), symmetric double precipitation peaks straddling the SST maximum (mode 2),and a single precipitation peak on one side of the SST maximum (mode 3).The three modes are due to different characteristics of the migration of convective activity centers.When convective activity moves to the flank of the SST maximum, the virtual effect of water vapor leads to surface lowpressure anomalies that further enhance convection.On the other hand, the surface low-pressure anomalies forced by the prescribed SST always locate over the SST maximum.When the SST gradient is weak, the virtual effect is weak and the mock-Walker cell is in mode 1.As the SST gradients increase, depending on whether the virtual effect can overcome the effects of SST, the convective activity may be trapped in a quasi-steady state on one side of the SST maximum (mode 3), or migrate between the two sides (mode 2).The off-center state precipitation mechanism might be related to the reduction of convection with high SST mentioned in previous research (Lau et al., 1997).

Fig.9.Selected cases from (a) Group S, (b) Group L, and (c) Group LW under simulations with a horizontal resolution of 2 km.(d) Simulations of Group L with a warmer background SST of 300 K.The rest of the settings are the same as in the corresponding original cases.A 4-point running mean is applied to (a) and (d); a 32-point running mean is applied to (b) and (c).
There are some limitations in this study.For example,the SST anomalies in some experiments here are unrealistically large.Besides, we were only able to examine three groups of experiments and two series of supplementary tests; SST anomalies with other distributions were not examined due to the limitation of time and computational resources.In addition, the ocean heat transport by oceanic dynamics and atmospheric feedbacks to the SST were not included in this study.If an interactive ocean model is used instead of the prescribed SST, the SST anomaly may be modified or damped.Nevertheless, our conclusions can be generalized and have implications for the tropical large-scale circulations (including the Hadley circulation) in the real atmosphere as well as general circulation models.The importance of the virtual effect of water vapor in the tropics is supported by other studies (e.g., Seidel and Yang, 2020; Yang et al.,2022).Moreover, the virtual effect increases as the climate warms.It is of interest to further explore the role of the virtual effect in the real tropical atmosphere under global warming.
Acknowledgements.This research was supported by the National Key R&D Program of China (Grant No.2022YFC3003902) and the National Natural Science Foundation of China (Grant No.42075146).
杂志排行
Advances in Atmospheric Sciences的其它文章
- Southern Hemisphere Volcanism Triggered Multi-year La Niñas during the Last Millennium
- Shallow Convection Dataset Simulated by Three Different Large Eddy Models
- Persistent Variations in the East Asian Trough from March to April and the Possible Mechanism
- Impact of Initial Soil Conditions on Soil Hydrothermal and Surface Energy Fluxes in the Permafrost Region of the Tibetan Plateau
- Climate-Vegetation Coverage Interactions in the Hengduan Mountains Area, Southeastern Tibetan Plateau, and Their Downstream Effects
- Cloud Top Pressure Retrieval Using Polarized and Oxygen A-band Measurements from GF5 and PARASOL Satellites※
