基于麻雀搜索算法的微电网分层优化调度
2024-03-25吴成明邢博洋李世春
吴成明,邢博洋,李世春
(1. 三峡大学电气与新能源学院,湖北 宜昌 443002;2. 新能源微电网湖北省协调创新中心(三峡大学),湖北 宜昌443002)
0 引言
微电网作为消纳可再生能源的有效手段,风能和太阳能等已广泛分布于其中[1],风、光出力的随机性使微电网的优化调度成为十分重要的课题[2]。
现阶段,微电网优化调度不仅是对供给侧可控电源的经济调度[3-6],还要考虑需求侧响应调节负荷。文献[7]考虑实时电价和用户满意度优化负荷曲线建立微电网双层优化模型;文献[8]建立分时电价机制下用户需求响应的微电网优化调度模型;文献[9]提出差异化需求响应机制,建立微电网运行成本最低的模型以上研究在优化负荷时均未考虑负荷对多余新能源出力的消纳。文献[10-11]考虑消纳新能源和分时电价优化负荷曲线,但未考虑用电满意度。
微电网优化调度属于非线性、多维度、多约束的复杂优化问题[12],智能算法作为求解此类问题的方法被广泛使用。目前应用较多的有粒子群算法(particle swarm optimization,PSO)和遗传算法等,但由于这些算法本身存在限制,寻优效果不太理想,除了对算法进行改进外[13-14],也使用了许多新型算法求解模型[15-16]。文献[17]改进鸡群算法(chicken swarm optimization,CSO)的学习更新策略和边界更新策略,与不同鸡群算法相比提升了算法的优化性能。文献[18]用改进多目标灰狼算法(grey wolf optimizer,GWO) 求解冷热电联供型微电网模型,具有较强的全局搜索性和较快的计算速度。文献[19]用蚁狮算法求解,与粒子群算法相比在收敛速度上占优。以上研究大多只将改进前后算法性能进行对比,与其他智能算法对比较少,不能充分证明算法的性能。
本文考虑需求响应建立了微电网的分层优化模型,上层以净负荷成本和用电满意度为目标,下层以运行成本和环境成本为目标,使用麻雀搜索算法(sparrow search algorithm, SSA)求解[20]。针对SSA易陷入局部最优[21]的问题提出一种改进麻雀搜索算法(improved sparrow search algorithm, ISSA)并将ISSA 改进成多目标算法。通过求解算例以及对比不同算法的迭代结果对模型和ISSA 的有效性进行验证。
1 微电网结构
本文对包含光伏阵列(photo voltaic, PV)、风力发电机(wind turbine, WT)、微型燃气轮机(micro turbine, MT)、柴油发电机(diesel engine,DE)和蓄电池(battery, BAT)、固定负荷和可转移负荷的并网型微电网进行研究,其结构如图1所示。

图1 微电网结构图Fig. 1 Diagram of microgrid structure
2 微电网分层优化模型
2.1 上层优化模型
2.1.1 目标函数
1) 为增加消纳新能源量,减少购电成本,建立净负荷成本最小的目标函数,如式(1)所示。
式中:CGD为购电成本,计算方法如式(2)所示;CQ为弃风、弃光惩罚成本,计算方法如式(3)所示。
式中:cbuy(t)为t时段购电价格;λ为弃风、弃光惩罚单价;ΔP(t)为优化后t时段的净负荷;PLnew(t)为优化后t时的负荷;PWT(t)、PPV(t)分别为t时段风、光出力;T为总时段,取值为24。
2) 负荷的转移会对用户的用电体验造成影响,为减小负荷转移对用户正常用电的影响,建立用电满意度最大的目标函数,如式(5)所示[11]。
式中PL(t)为优化前t时段的负荷。
3) 上层模型的两个目标函数量纲不同,建立上层目标函数,如式(6)所示。
2.1.2 约束条件
1) 优化前后负荷总量不变,存在等式约束,如式(7)所示。
2) 可转移负荷有上下限,存在不等式约束,如式(8)所示。
式中ε为可转移负荷占比。
2.2 下层优化模型
2.2.1 目标函数
1) 为使微电网经济效益最大化,建立运行成本最小的目标函数,如式(9)所示。
式中:CRL、CYW和CG分别为微电网的燃料成本、运维成本和微电网与主网功率交互费用,分别如式(10)—(12)、(13)和式(14)—(15)所示。
式中:CDE、CMT分别为柴油发电机、微型燃气轮机燃料成本;PDE(t)、PMT(t)分别为t时段柴油发电机、微型燃气轮机输出功率;α、β和γ为柴油发电机燃料成本系数;cm和LHV分别为天然气价格和低热值;η为微型燃气轮机发电效率。
式中:N为可控发电单元数目:Pn(t)为t时段可控发电单元n输出功率:Kn为可控发电单元n运维费用系数:KB为蓄电池运维费用系数:PB(t)为t时段蓄电池充放电功率,正为放电,负为充电。
式中:PG(t)为t时段微电网与主网交互功率,正为购电,负为售电;c(t)为t时段微电网与主网交互功率价格;csell(t)为t时售电价格;cbuy(t)为t时段购电价格。
2) 为减少微电网发电过程中对环境的污染,建立环境成本最小的目标函数,如式(16)所示。
式中:M为污染物类型;N1为产生污染物的发电单元数目;km为m污染物治理费用系数;rnm为可控发电单元n产生m污染物排放量系数。
3) 下层模型的两个目标函数有相同的量纲,建立下层目标函数,如式(17)所示。
2.2.2 约束条件
1) 微电网中每个时刻应保证功率平衡,存在等式约束,如式(18)所示。
2) 可控发电单元输出功率有限制,存在不等式约束,如式(19)所示。
式中Pnmax、Pnmin分别为可控发电单元n输出功率上、下限。
3) 为保证蓄电池的使用寿命,其充放电功率存在不等式约束,如式(20)—(22)所示。
式中:Pdcmax和Pcmax分别为蓄电池最大放电功率和充电功率;SOC(t)为t时段蓄电池荷电状态;SOCmax、SOCmin分别为荷电状态上下限;ΔSOC为荷电状态变化量;E为蓄电池容量;ηc和ηd分别为蓄电池充、放电效率。
4) 微电网与主网联络线上可流过功率有限制,交互功率存在不等式约束,如式(23)所示。
式中PGmax、PGmin分别为微电网与主网交互功率上、下限。
3 模型求解方法
3.1 麻雀搜索算法(SSA)
SSA 模拟麻雀觅食过程,依据适应度将种群排序,分为发现者、加入者和警戒者。选择排序在前的麻雀为发现者,位置更新如式(24)所示[22]。
式中:Xi,j为第i只麻雀在第j维的位置信息;t为迭代次数;itermax为最大迭代次数;α∈(0,1]为随机数;R2∈[0,1]和ST∈[0.5,1]为预警值和安全值;Q为服从正态分布的随机数;L为元素全部为1 且与X同维度的矩阵。
剩余麻雀为加入者,向发现者靠近的同时在自身周围广泛搜索,位置更新如式(25)所示[22]:
式中:Xp为目前发现者最优位置;Xworst为目前麻雀最差位置;A+=AT(AAT)-1,A为与X同维度的矩阵,其中元素随机赋值1或-1;n为加入者数量。
随机选择种群中麻雀作为警戒者,位置更新如式(26)所示[22]:
式中:Xbest为目前麻雀最优位置;β为服从均值为0,方差为1的正态分布的随机数;K∈[-1,1]为随机数;fi为第i只麻雀适应度;fb和fw分别为目前麻雀最优适应度和最差适应度;φ为很小的数,避免分母为0。
3.2 改进麻雀搜索算法(ISSA)
3.2.1 改进发现者公式
针对SSA 易陷入局部最优的问题,依据量子粒子群算法,认为发现者具有量子行为来增强其全局搜索能力,并且引入全局最优个体位置,提高麻雀种群信息利用率[23],改进发现者位置更新公式如式(27)所示:
式中:GXb为全局最优个体位置;δ为自适应扩张系数;u为[0,1]间的随机数。
3.2.2 变异、贪婪策略
加入变异、贪婪策略[24],增加种群多样性,增强算法跳出局部最优的能力,如式(28)—(30)所示。
式中:r为自适应变异概率:Xu和Xl分别为初始上下限;Xmu和Xml分别为变异上下限;Xm为变异后的位置;R、m∈[0,1]为随机数。
3.2.3 多目标改进
由于求解上层模型属于多目标寻优,所以作出如下改进。
1) 加入非支配排序[25-26]:将麻雀按第一个目标函数值从小到大排序后,从第二个麻雀开始,依次序与前面麻雀比较第二个目标函数值的大小,若大于前一个麻雀,记为被支配一次,最后记下每个麻雀被支配次数,按被支配次数从小到大进行排序,即为非支配排序结果。
2) 多目标寻优时,将被支配次数为0的麻雀存入外部存储空间,使用轮盘赌法[27]从外部存储空间中选取GXb,若外部存储空间为空,则选取非支配排序第一位的麻雀为GXb。
3) 多目标适应度无法代入式(26),所以进行改进如式(31)所示:
3.3 求解流程
基于麻雀搜索算法的微电网分层优化模型具体流程如图2所示,求解思路如下。

图2 模型求解流程图Fig. 2 Flowchart of model solution
1) 在上层模型中,输入算法和算例参数。以式(7)—(8)为约束条件,式(6)为目标函数,生成上层初始种群,使用多目标ISSA 迭代求解出Pareto前沿。
2) 使用基于信息熵确立权重的TOPSIS 法在Pareto 前沿中选择折中解,步骤如下:先按式(32)对目标函数进行无量纲化处理[28];再按式(33)和(34)求出目标函数熵值和熵权[28];最后代入式(35)计算[29],选取FXq大的解为折中解。
式中:和为Pareto 前沿中个体q第p个目标函数值和无量纲化值;和为Pareto 前沿中第p个目标函数的最大值和最小值;Q为Pareto 前沿中个体数量;P为目标函数数量;Hp和ωp为第p个目标函数的熵值和熵权;FXq为个体q的评价指标。
3) 在下层模型中,以式(18)—(23)为约束条件,式(17)为目标函数,生成下层初始种群,使用单目标ISSA迭代求解出最优个体。
4 算例及结果分析
4.1 算例参数
调度周期T=24 h,PV、WT 出力及负荷曲线如图3 所示。弃风、弃光惩罚单价为0.3 元/kWh。售电和购电价格如表1所示。

表1 购电和售电价格Tab. 1 Purchase and sale prices of electricity

图3 PV、WT出力及负荷曲线Fig. 3 Curves of PV、WT output and load
微电网各单元参数如表2 所示。蓄电池参数如表3 所示。污染物参数如表4 所示。微电网与主网交互功率限值为30 kW。DE 燃料成本系数α、β和γ 分别为0.000 85、0.11、6;MT 发电效率30%,天然气价格2.5 元/m3,低热值9.7 kWh/m3。

表2 微电网各单元参数Tab. 2 Parameters of each unit of the microgrid

表3 蓄电池参数Tab. 3 Parameters of storage battery

表4 污染物参数Tab. 4 Contaminant parameters
4.2 结果分析
4.2.1 上层优化结果
分别求解ε为10%和20%的情况,得出Pareto前沿如图4所示,负荷优化曲线如图5所示。
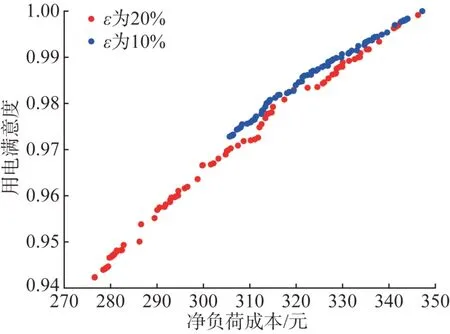
图4 Pareto前沿Fig. 4 Pareto frontier

图5 不同ε的负荷优化曲线Fig. 5 Load optimization curves under different ε
由图4 可知,考虑需求响应后,净负荷成本越低,用电满意度就越低;ε越大,净负荷成本和用电满意度可变化范围越大。
由图5可知,优化后的负荷曲线在11时—14时增加了需求量,在15 时—22 时减少了需求量,其余时刻基本无明显变化,起到一定削峰填谷的作用。
对比不同ε下的用电满意度和净负荷成本,如表5所示。
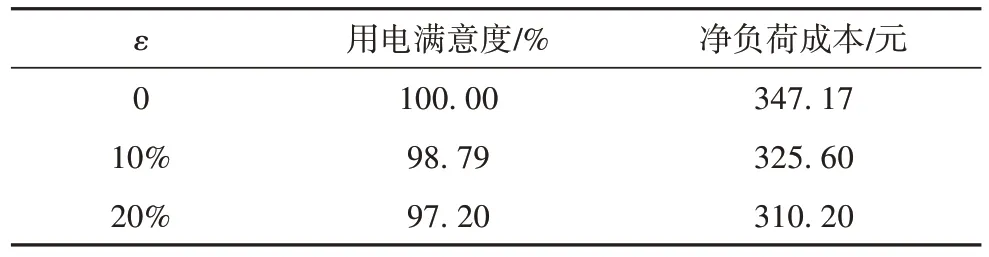
表5 不同ε下的负荷优化结果Tab. 5 Load optimization results under different ε
由表5 可知,不考虑需求响应,即ε为0 时用电满意度为100%,净负荷成本为347.17 元。考虑需求响应后,当ε为10%时用电满意度为98.79%,净负荷成本为325.60 元,相较于ε为0 时用电满意度下降1.21%,净负荷成本下降21.57 元(6.21%);当ε为20%时用电满意度为97.20%,净负荷成本为310.20 元,相较于ε为0 时,用电满意度下降2.80%,净负荷成本下降36.97 元(10.65%),而对比ε为10%时用电满意度下降1.59%,净负荷成本下降15.4 元(4.73%)。
综上可知,选取ε为10%时可以在小幅降低用电满意度的前提下大幅减少净负荷成本,性价比较高。
4.2.2 下层优化结果
依据不同ε下优化后的负荷曲线,求解出各情况下的各可控发电单元的调度曲线,如图6所示。

图6 3种情况下的调度曲线Fig. 6 Schedule curves in 3 scenarios
由图6 可知,从1 时—16 时以及24 时,微电网通过和主网交互电能以及BAT 来满足负荷需求,DE 和MT 未启用;从17 时—23 时,微电网从主网购电无法满足负荷需求,启用MT 供电,始终未启用DE。对比图6(a)、(b)和(c)可知,考虑需求响应后MT 发电量减少,谷时段和平时段从主网购电量增加。
对比不同ε调度结果下微电网运行成本、环境成本和综合成本,如表6所示。
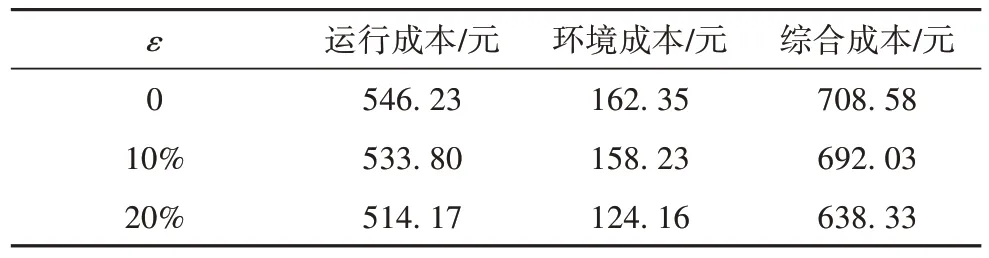
表6 不同ε下的微电网成本Tab. 6 Microgrid costs under different ε
由表6 可知,不考虑需求响应,即ε为0 时运行成本为546.23 元,环境成本为162.35 元,综合成本为708.58 元。考虑需求响应后,当ε为10%时运行成本为533.80 元,环境成本为164.59 元,综合成本692.03 元,相较于ε为0 时运行成本减少12.43 元(2.28%), 环境成本减少4.12 元(2.53%),综合成本减少16.55 元(2.34%);当ε为20% 时运行成本为514.17 元,环境成本为124.16 元,综合成本为638.33 元,相较于ε为0时运行成本减少32.06 元(5.87%),环境成本减少38.19 元(23.5%), 综合成本减少70.25 元(9.91%)。
综上可得,考虑需求响应,能减少微电网的综合成本,ε越大,综合成本降低越多。但是结合上下层优化结果,选择ε为10%时能够协调微电网供需两侧的利益。
4.2.3 算法性能对比
用ISSA、SSA、PSO[13]、CSO[15]和GWO[16]求解ε为10%时的下层模型,设定种群数量为100,迭代次数为500,ISSA 和SSA 参数设置相同,PSO、CSO 和GWO 参数分别依照文献[13]、[15]和[16]设置,迭代曲线如图7所示。

图7 算法迭代曲线Fig. 7 Algorithm iteration curves
由图7 可知,ISSA 相较于SSA 和CSO 收敛速度和寻优效果都有提升;ISSA 与PSO 和GWO 相比收敛速度稍慢,但寻优效果优于PSO和GWO。
将不同算法20 次迭代的结果取平均值最小值和标准差[30],如表7所示。
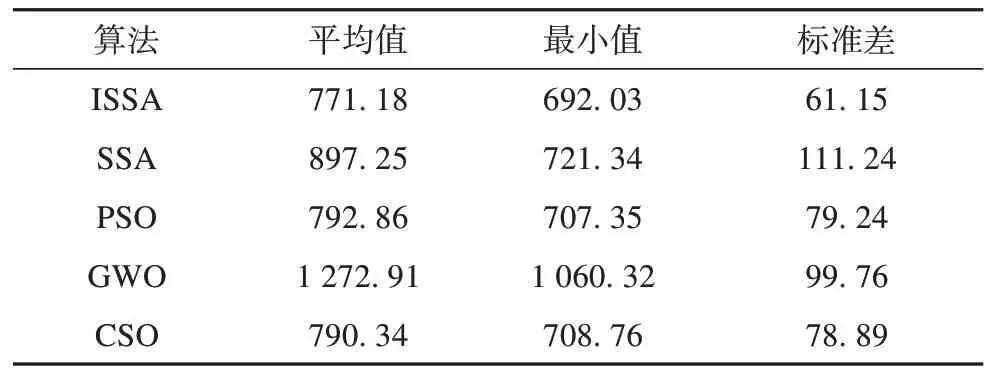
表7 不同算法求解结果Tab. 7 Solution results of different algorithms
由表7可知,ISSA 求解结果的最小值、平均值和标准差都优于其余算法,证明ISSA 寻优效果和稳定性最好。
将文献[30]的改进SSA 记为WSSA,把ISSA、SSA和WSSA的迭代曲线进行对比,如图8所示。

图8 不同SSA迭代曲线Fig. 8 Iteration curves of different SSA
由图8 可知,SSA 与WSSA 在迭代过程中,陷入局部最优后,经过多次迭代才能跳出,影响了算法的收敛,而ISSA 可以很快地跳出局部最优,大大提高了算法的收敛速度,增强了算法的搜寻能力。
5 结语
本文针对考虑需求响应的并网型微电网优化调度问题建立分层优化模型,提出ISSA 进行求解,最后通过算例求得结果。分析可知:本文的微电网分层优化模型中可转移负荷占比为10%时,能够在保证用户用电满意度的同时增大新能源消纳量,节省微电网的综合成本,协调供需两侧的利益,且ISSA 具有良好的寻优性能,在求解此问题上具有一定的优越性。
