Effects of thawing-induced softening on fracture behaviors of frozen rock

Ting Wng,Hiling Ji,Qing Sun,Xinjun Tn,Liyun Tng

a College of Geology and Environment, Xi’an University of Science and Technology, Xi’an, 710054, China

b College of Architecture and Civil Engineering, Xi’an University of Science and Technology, Xi’an, 710054, China

c State Key Laboratory of Geomechanics and Geotechnical Engineering,Institute of Rock and Soil Mechanics,Chinese Academy of Sciences,Wuhan,430064,China

Keywords: Frozen sandstone Different thawing temperature Fracture toughness Microcrack propagation process Unfrozen water content

ABSTRACT Due to the presence of ice and unfrozen water in pores of frozen rock,the rock fracture behaviors are susceptible to temperature.In this study,the potential thawing-induced softening effects on the fracture behaviors of frozen rock is evaluated by testing the tension fracture toughness (KIC) of frozen rock at different temperatures(i.e.-20 °C,-15 °C,-12 °C,-10 °C,-8 °C,-6 °C,-4 °C,-2 °C,and 0 °C).Acoustic emission (AE) and digital image correlation (DIC) methods are utilized to analyze the microcrack propagation during fracturing.The melting of pore ice is measured using nuclear magnetic resonance(NMR)method.The results indicate that:(1)The KIC of frozen rock decreases moderately between-20 °C and -4 °C,and rapidly between -4 °C and 0 °C.(2) At-20 °C to-4 °C,the fracturing process,deduced from the DIC results at the notch tip,exhibits three stages: elastic deformation,microcrack propagation and microcrack coalescence.However,at -4 °C-0 °C,only the latter two stages are observed.(3) At-4 °C-0 °C,the AE activities during fracturing are less than that at -20 °C to -4 °C,while more small events are reported.(4) The NMR results demonstrate a reverse variation trend in pore ice content with increasing temperature,that is,a moderate decrease is followed by a sharp decrease and-4 °C is exactly the critical temperature.Next,we interpret the thawing-induced softening effect by linking the evolution in microscopic structure of frozen rock with its macroscopic fracture behaviors as follow:from-20 °C to-4 °C,the thickening of the unfrozen water film diminishes the cementation strength between ice and rock skeleton,leading to the decrease in fracture parameters.From-4 °C to 0 °C,the cementation effect of ice almost vanishes,and the filling effect of pore ice is reduced significantly,which facilitates microcrack propagation and thus the easier fracture of frozen rocks.

1.Introduction

Increasing global warming now leads to numerous large-scale,high-potential rock slope failures,rockfalls,and other geological hazards in alpine regions(Gruber and Haeberli,2007;Gobiet et al.,2014),and it brings serious threats to infrastructure,human life,and property safety(Phillips,2006;Huggel et al.,2008).Numerous evidences indicate that melting of the permafrost in high mountains is a major factor for destabilization of rock slope(Huggel et al.,2010;Ravanel et al.,2010;Etzelmüller et al.,2022).Mountain permafrost is generally characterized by thick frozen bedrock,and the mechanical properties of which primarily determine the stability of rock slopes in high mountains (Harris et al.,2009;Phillips et al.,2017).Fracture toughness(KC),a common mechanical parameter of frozen rock,can be considered as a criterion of fracture initiation and propagation to estimate the instability of rock slopes (Fischer et al.,2010;Krautblatter et al.,2013).Due to the coexistence of unfrozen water and ice in pores of frozen rock,its fracture behaviors are susceptible to temperature change.Thus,investigating the fracture behaviors of frozen rock during thawing is crucial for engineering activities in mountain permafrost regions.

In fracture mechanics,there are basically three modes of rock fracturing (Whittaker et al.,1992): tension (mode I),sliding shear(mode II),and tearing shear mode (mode III).As a result of the comparatively low tensile strength of rocks,tension fracture is the most common in failure analysis of rock slopes (Stead and Wolter,2015;Chen et al.,2021).In addition,tension fracture is encountered in other areas of rock engineering(He et al.,2010;Zhou et al.,2018),including hydraulic fracturing (Pan et al.,2021),shale gas extraction (Li et al.,2019),and deep nuclear waste (Peng et al.,2020).Therefore,numerous researches have been conducted on the tension fracture properties of rocks,including test methods of tension fracture toughnessKIC(Muñoz-Ibáñez et al.,2021;Kramarov et al.,2020),various influence factors (Cai et al.,2020;Deng et al.,2021)and fracturing process(Lin et al.,2020;Han et al.,2022).

Previous researches have provided a basic understanding of the tension fracture process of rock.The International Society of Rock Mechanics and Rock Engineering (ISRM) proposed four standard ways to testKIC,namely,the short rod (SR),chevron bend (CB),cracked chevron notched Brazilian disc(CCNBD)and semi-circular bend(SCB)methods(Kuruppu et al.,2014).Studies on the influence factors ofKICshow that in addition to lithology and water content,temperature also has a significant influence.At high or low temperatures,the fracture toughness of rocks differs greatly from that at room temperature(Dwivedi et al.,2000;Feng et al.,2017;Miao et al.,2020).For the tension fracture,due to the singularity of cracks,a rather extensive plastic zone,termed as the fracture process zone(FPZ),is generated by microcracks around the cracks’tips.Variation of the FPZ directly influences the fracture propagation process(Pan et al.,2021).Methods such as digital image correlation(DIC) and acoustic emission (AE) (Wong and Guo,2019;Lin et al.,2020) have been frequently employed to determine the range of FPZ and investigate its evolution(Wei et al.,2015;Wu et al.,2011;Lin and Labuz,2013).

While previous researches on frozen rock are mainly focused on the strength,deformability and failure features(Jia et al.,2020a)or the effects of freeze-thaw cycles on its mechanical properties(Jamshidi et al.,2017;Jia et al.,2020b;Zhu et al.,2021;Jamshidi,2021;Wang et al.,2022;Ren et al.,2022),little attention is paid to the fracture behaviors of frozen rock.Heating of frozen rock leads to melting of the pore ice and hence alters the pore structure of the rock,which will have a substantial effect on the fracture mechanical properties of frozen rock (Wang et al.,2022).Investigating the fracture behaviors of frozen rock becomes challenging.However,a proper evaluation of the effects of thawing on the fracture features of frozen rock is rarely reported.For this,a series of semi-circular bending (SCB) tests of frozen rocks at different thawing temperatures(T=-20°C,-15°C,-12°C,-10°C,-8°C,-6°C,-4°C,-2°C and 0°C) were conducted.AE and DIC techniques were then utilized to monitor the AE signals and surface strain of the sample during microcrack propagation,and the impact of thawing was also analyzed.The nuclear magnetic resonance(NMR)method was used to examine the change in unfrozen water content of rock.Combined with the change of unfrozen water content and microcrack propagation process,the mechanism of how thawing modifies the fracture behaviors of frozen rock was discussed.

2.Methodology

2.1.Test method of KIC

The SCB samples are used in this study to evaluate theKICof frozen rock due to the easy preparation and testing procedure(Kuruppu et al.,2014).The size of the SCB sample is determined as shown in Fig.1a,and theKICis calculated according to Eq.(1)-(2)in Kuruppu et al.(2014).

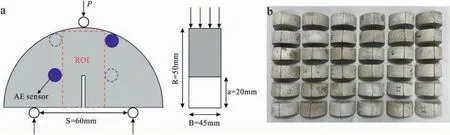
Fig.1.(a) Size of SCB sample;and (b) SCB rock samples.

2.2.Digital image correlation (DIC) method

DIC can be used to accurately measure optical surface deformation.The device consists of a light,a charge coupled device(CCD) camera,and a computing apparatus with relevant software.The correlation calculation approach is used to calculate the deformation information by analyzing the two images before and after deformation.The deformation analysis process of DIC is as follows:

(1) A pre-deformation image is selected as the reference image and the region of interest is determined (see Fig.2);

Fig.2.The DIC method to calculate deformation.

(2) By specifying the subset size and distance,the region of interest is meshed to obtain uniformly spaced virtual grids;

(3) A group of pixels on each point of the virtual grid is defined as a subset.It is assumed that each subset is in a rigid motion,ignoring the deformation of the subset itself.Then,correlation calculations are performed on each subset using a predefined correlation function and certain search strategies.In the deformed image,the region that has the strongest correlation with the reference subset is determined as the target subset,which marks the position of the reference subset after deformation,and the displacement between them is obtained accordingly(Fig.2) (Pan and Li,2011);and

(4) The deformation information of the whole field can be obtained by computing all subsets.A zero-mean normalized sum of squared difference is utilized as the similarity measure of the reference and the target subsets in this study due to its robustness to scale and offset variations of illumination as well as its simplicity for optimization (Pan et al.,2010).

2.3.NMR method

If a rock sample is in the permanent magnet field of the NMR equipment,the hydrogen (H) protons of pore water generate magnetization vectors along the direction of the magnetic field.While a pulsed electromagnetic field is emitted,these H protons flip to a new equilibrium position,and then back to its original equilibrium position as the alternating electromagnetic field is withdrawn.This process is called relaxation.During the relaxation,the H protons will cut the magnetic flux line and produce an electrical signal,and the electrical signals continues to decay,which is called free induction decay (FID).The NMR signals of FID are positively correlated with the number of water molecules (Zhao et al.,2017).While,the NMR signals of H protons in ice can hardly be detected in low-intensity magnetic field.Therefore,the NMR signals of FID can be used to determine the liquid water (i.e.unfrozen water) content in frozen rock and soils (Tice et al.,1982;Watanabe and Wake,2009):

The ice content can be calculated by

whereSrwis the relative unfrozen water content(%),FIDfrozenis the NMR signals of FID at different thawing temperatures,FIDunfrozenis the FID value at 20°C,andSriis the relative ice content (%).

2.4.Experimental design

2.4.1.Sample preparation

(1)Petrographic studies.The sample used in this study is yellow feldspar quartz sandstone bearing a massive structure without obvious bedding layers.In addition,it is composed of 90% quartz,5% feldspar sand and 5% Kaolinite.Fig.3 exhibits the single polarized and orthogonal polarized microscopic thin-section images of the sandstone.

Fig.3.(a) The single polarized;and (b) orthogonal polarized microscopic thin-section images.

(2)SCB sample preparation.Twenty two cylindrical samples(diameter×height:100 mm×45 mm)were drilled from the same sandstone block.They were oven-dried at 105°C and placed in a vacuum-saturated cylinder to pump for 4 h under-0.1 MPa.Water was then injected into the saturated cylinder to completely immerse the sample,the water-saturated mass of samples was measured after 72 h,and their porosity was determined.The Pwave test of each sample was also conducted.Among the 22 cylindrical samples,18 samples with similar porosity and P-wave velocity were selected and sliced into 36 semicircle SCB samples(Fig.1b).The dry density of samples was (2.1 ± 0.1) g/cm3,the porosity of samples was(19.18 ±0.2)%,and the P-wave velocity of samples was (2.37 ±0.6) km/s.

Thirty six saturated SCB samples were wrapped with plastic films and placed in a moisturizing vat(at 20°C,relative humidity of 50%) for a week to ensure uniform water distribution inside the samples.The samples were then frozen for 48 h in an environmental chamber at -20°C.In order to conduct the DIC test,the sample’s surface should be treated before the test to show random speckle patterns.Therefore,the surface of specimens was first painted white;once the white paint dried,black dots were dotted with a marker to create randomly scattered speckle patterns.

2.4.2.Tests of KIC

TheKICtests at different temperatures were carried out via a hydraulic servo press,which is equipped with a high-precision environmental chamber (Fig.4a).Loading was controlled by the axial displacement at a rate of 0.12 mm/min,which satisfies the ISRM’s recommendation that the loading rate of the SCB test should not exceed 0.2 mm/min.The chamber has a temperature control accuracy of ±0.1°C.

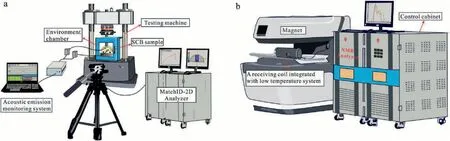
Fig.4.(a) The press machine which is fitted out with a high-precision environment chamber,and the AE and DIC strain capture systems;and (b) NMR test system.

The lower temperatures limit in cold regions (except in polar regions)is usually above-20°C(Ma et al.,2022),thus it is rational to set -20°C as the starting point of thawing for frozen rock.TheKICof 36 SCB saturated samples at nine thawing temperatures(T=-20°C,-15°C,-12°C,-10°C,-8°C,-6°C,-4°C,-2°C,and 0°C)were tested.The testing steps are as follows:a frozen sample is taken out from the-20°C chamber,and four AE probes are fixed on the sample according to the positions given in Fig.1a,and it is then placed back in the chamber equipped to the press,as shown in Fig.4a.Afterwards,the temperature of the chamber was set as a preset test temperature and kept for 4 h,and theKICtest was conducted.

The DS5-8B AE instrument (Beijing Softland Times Technology Co.,Ltd.)was employed to record AE signals during sample loading.The AE system can collect data at a rate of 3 Mhz (Fig.4a).The preamplifier and trigger threshold of AE acquisition system are both set as 40 dB.

The variation of surface strain during loading was analyzed using the MatchID-2d/Stereo full field strain measurement system(Fig.4a).A photon FASTCAM Mini UX100 camera was vertically fixed at a tripod 0.5 m away from the press machine.The frame rate is 50 fps(frames per second),and the light source is LED cold light.

2.4.3.Measurement of the unfrozen water content in frozen rock during thawing

The MacroMR12-150H NMR instrument (Suzhou Niumai Analyzer Co.,Ltd.)is used in this study(Fig.4b).A low temperature control system is equipped with NMR receiving coil,and it can provide a uniform subzero temperature field.The parameters for NMR test is the same as that of Wang et al.(2021).The following are the steps for measuring the unfrozen water content of frozen rock during thawing:(1)A sample was firstly placed in the receiving coil and the temperature is set as-20°C;(2)After 4 h,the NMR test is conducted;(3)The temperatureTis then set to-15°C,-12°C,-10°C,-8°C,-6°C,-5°C,-4°C,-3°C,-2°C,-1°C,0°C and 20°C,successively,and (4) the NMR signal is measured at each temperature after 4 h.

3.Results

3.1.Changes in KIC and fracture energy during thawing

TheKICrepresents the capacity of a rock to resist unstable propagation of cracks.The fracture energy refers to as the required energy per unit area of crack propagation,which is dissipated during crack propagation.The two parameters are used to describe the initiation and propagation of cracks for assessing the fracture characteristics of rocks.

TheKICof frozen rock at various thawing temperatures is displayed in Fig.5a.It drops remarkably due to thawing and exhibits a two-stage mode of (a) slow decrease,KICdeclined by 19.5% asTdrops from-20°C to-4°C;and(b)rapid decrease,KICdeclined by 74%as-4°C ≤T<0°C.Therefore,-4°C is a critical temperature that marks the starting of rapid decrease inKICof frozen rock during thawing.

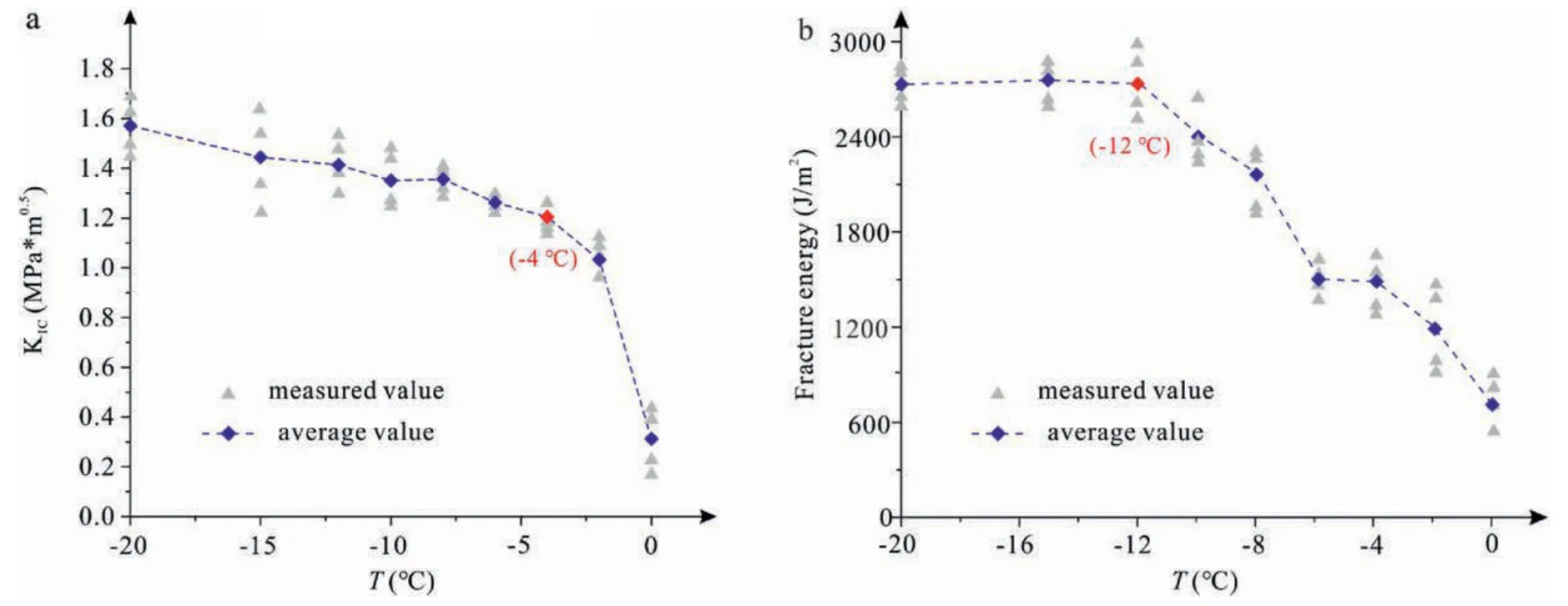
Fig.5.(a) Changes of KIC and (b) fracture energy during thawing.

During the SCB sample fracture,the fracture energy can be computed by the work done by the press system on the sample during loading,that is,the area is enclosed by the axial loaddisplacement curve before fracture (Peng et al.,2020).Based on this,the fracture energy of samples at various temperatures is displayed in Fig.5b.It shows that the fracture energy falls dramatically as the temperature increases and also exhibits a twostage mode of being essentially unchanged from-20°C to-12°C and rapidly reduces from-12°C to 0°C.

3.2.Influence of thawing on fracture process of frozen rock

Fig.6 illustrates the evolution of horizontal strain (HS) at the notch tip of SCB samples during fracture at various temperatures.It shows that the HS increases with the rise of axial stress,and thawing plays a dominant role.As -20°C ≥T>-4°C (Fig.6a-f),the HS vs.displacement curve exhibits a three-stage mode of (I)changeless stage;(II) moderate increase stage;and (III) rapid increase stage.At-4°C ≤T<0°C(Fig.6g-i),it exhibits a two-stage mode of(II)moderate increase stage,and(III)rapid increase stage.The mode I stage is not observed.

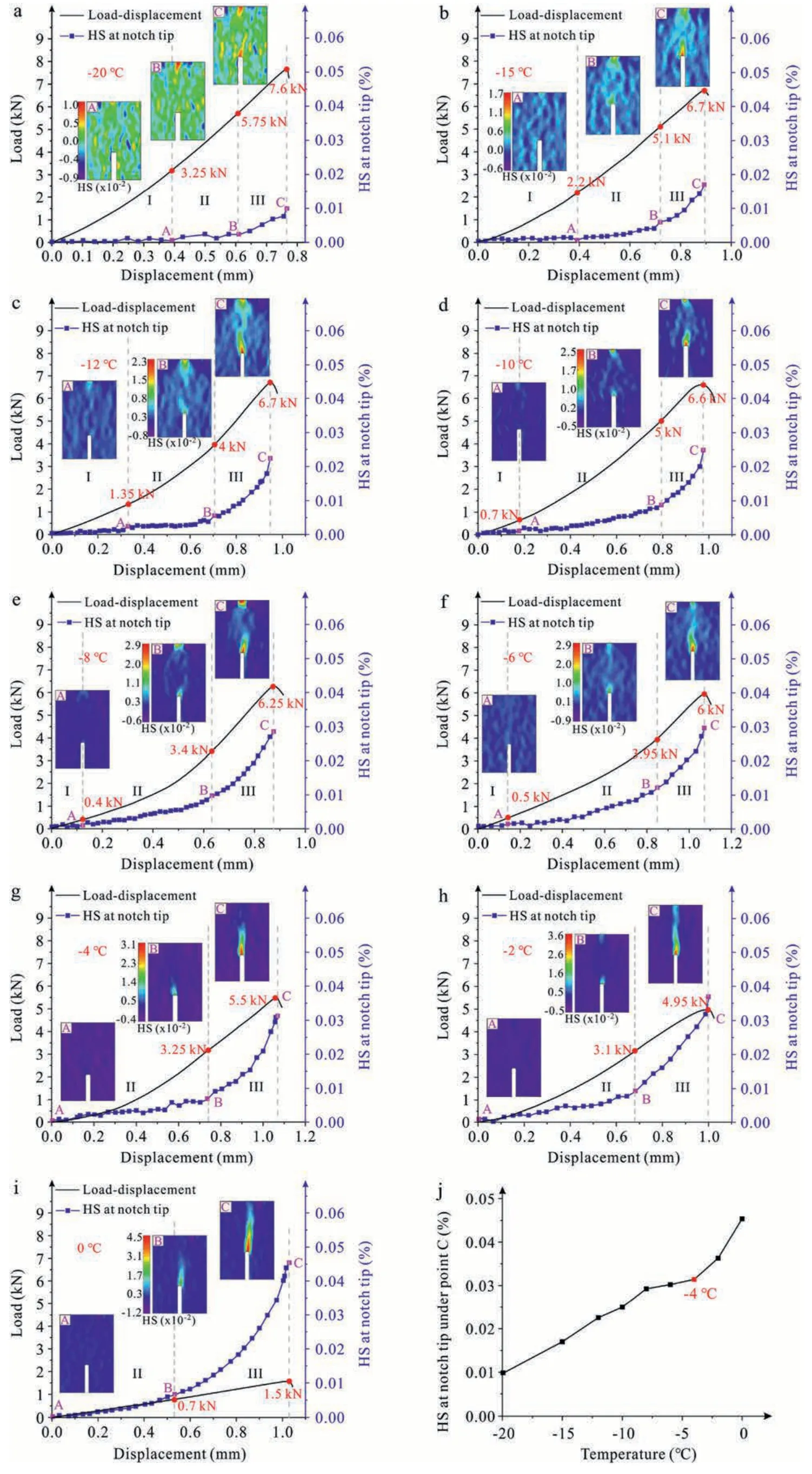
Fig.6.(a-i)Variations in HS at notch tip during fracture at different temperatures of-20 °C;-15 °C;-12 °C;-10 °C;-8 °C;-6 °C;-4 °C;-2 °C;and 0 °C;and(j)HS of notch tip under peak load at different temperatures.

(1) At -20°C ≥T>-4°C (Fig.6a-f),in the changeless stage(mode I),the HS is essentially unaffected by increase in the displacement and horizontal strain field (HSF) is basically evenly distributed(HSF at pointAon the HS vs.displacement curve).This suggests that the sample is undergoing a vertically elastic compression stage and the horizontal strain localization does not appear.In the moderate increase stage(mode II),the HS increases linearly as the displacement increases,and the HS around the notch tip is much higher than that in other regions(pointB),and this local region is the FPZ.The presence of FPZ implies the occurrence of strain localization due to expansion of the microcracks.In the rapid increase stage (mode III),the HS grows rapidly and the FPZ expands substantially(pointC).It demonstrates that the FPZ gradually develops,and as the microcrack coalesces,the precut macrocracks grow.Therefore,when the temperature is between-20°C and-4°C,the three stages of HS variation actually correspond to three stages in microcrack evolution at the notch tip of frozen rock: elastic deformation stage,microcrack propagation stage,microcrack coalescence stage.

(2) At -4°C ≤T<0°C (Fig.6g-i),in mode II stage,the HS increases linearly and the FPZ(pointB)occurs,indicating that microcracks have propagated.At the mode III stage,the HS grows rapidly and the FPZ range expands significantly(pointC),which is the precursor of microcrack propagation.The absence of the changeless stage suggests that microcracks at the notch tip of frozen rock are more likely to propagate at higher temperatures.

(3) Aiming to understand the effect of thawing on microcrack propagation in frozen rock,the HS at the notch tip of peak load (pointC) is measured at various temperatures,as depicted in Fig.6j.The HS at the notch tip grows approximately linearly with temperature increasing from -20°C to-4°C,while the increase in HS accelerates as temperature surpasses-4°C.This result indicates that thawing induces a significant softening effect on the fracture behaviors of frozen rock,and confirms again that -4°C is a critical temperature for the softening effect.

According to the above analyses,pointAindicates initiation of the microcrack propagation,pointBdenotes the beginning of microcrack coalescence,and pointCsignifies the occurrence of macrocrack propagation.Therefore,loads at pointA,pointBand pointCcan be marked as the microcrack propagation load,microcrack coalescence load and macrocrack propagation load,respectively.The three loads are extracted and their variation trend with temperature is illustrated in Fig.7.It demonstrates that the thawing leads to a gradual decrease in microcrack propagation load,microcrack coalescence load,and macrocrack propagation load,and they all change in two stages.At-20°C to-4°C,the load at pointAis decreased to 0 kN,and the loads at pointBand pointCare moderately decreased.From-4°C to 0°C,the loads at pointsBandCfall rapidly,while the load at pointAremains constant at 0 kN.

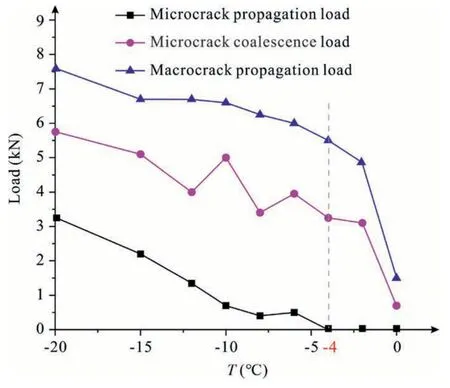
Fig.7.The variations in microcrack propagation load,microcrack coalescence load,and macrocrack propagation load at different thawing temperatures.

As shown in Fig.6(pointC),the range of FPZ varies at different temperatures.The FPZ at the peak load depicts the result of microcrack propagation and coalescence prior to macro-fracture.Therefore,many scholars determine the range of FPZ by the variation of the HSF,or displacement field (Wu et al.,2011;Lin et al.,2019).The method of determining the FPZ length by displacement field is shown in Fig.8a and b.

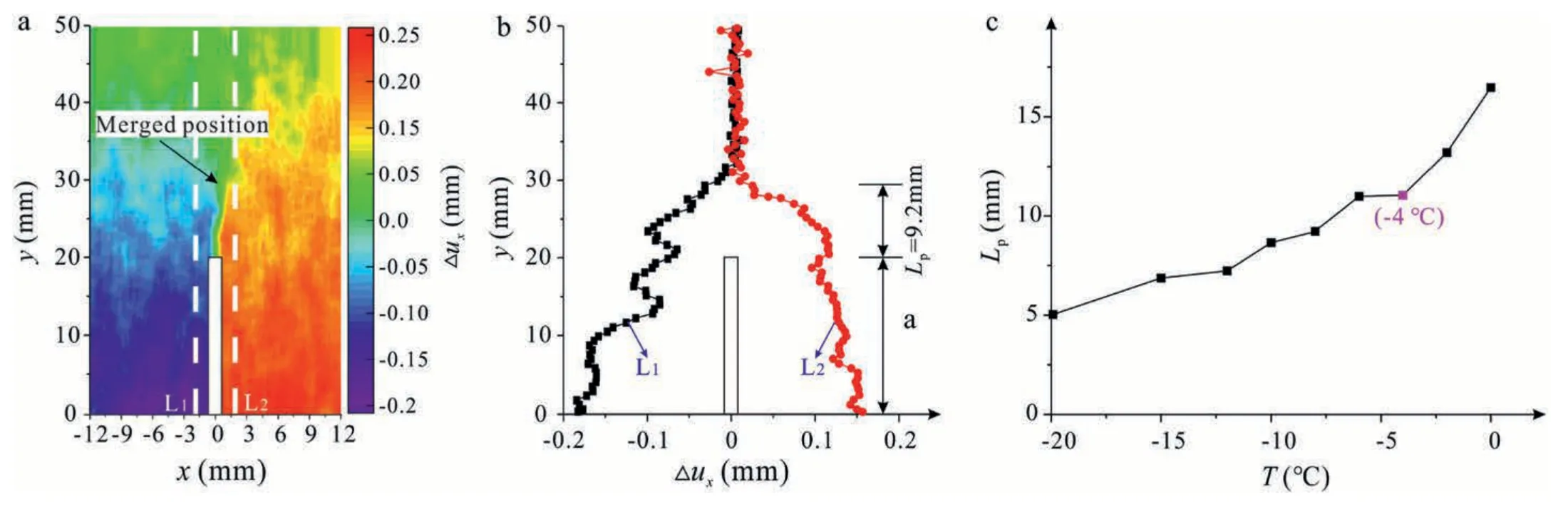
Fig.8.(a) Incremental horizontal displacement contours at peak load;(b)opening displacements along the notch of the sample at -8 °C;and (c) FPZ length at different thawing temperatures.

Fig.8a shows the incremental horizontal displacement contours on the sample surface as computed by DIC.To reduce the calculation error,horizontal displacement values on two reference lines along the notch length 2 mm to the side of the notch are extracted(the lines of L1and L2in Fig.8a),and shown in Fig.8b.The distance between the notch tip and the confluence point of two horizontal displacement lines delineates the length of FPZ:Lp(Lin and Labuz,2013).Fig.8c depicts the variation of FPZ length at the peak load with temperatures.Due to thawing,the FPZ length increases and demonstrates a two-stage mode of (a) moderate increase and (b)rapid increase.Unsurprisingly,the increase in FPZ length begins to accelerate at -4°C.

3.3.The influence of thawing on AE signals during fracturing of frozen rock

3.3.1.Changes in AE counts and cumulative AE counts

The changes in AE signals during fracturing of frozen rock under various testing temperatures are shown in Fig.9.At the beginning of loading,the AE counts are weak;with expansion of the microcrack,the AE counts rise.The cumulative AE counts grow in stages during microcrack propagation and exhibit a strong correlation with the change of HS.However,variation of the AE counts is sensitive to the temperature.

At-20°C ≥T>-4°C,the AE counts gradually intensify during microcracks expansion.The cumulative AE counts rise in three stages (Fig.9a-f).In the elastic deformation stage,microcracks basically do not expand,and the cumulative AE counts rise slowly.In the microcrack propagation stage,increase in the cumulative AE counts is greater;while in the microcrack coalescence stage,the cumulative AE counts rise rapidly.However,as the testing temperature rises over-4°C,the AE counts are much lower than that at-20°C to-4°C(Fig.9g-h).Moreover,the cumulative AE counts grow in two stages: a slow increase during the microcrack propagation stage and a rapid increase during the microcrack coalescence stage.When the ice in the sample is completely melted (0°C),the AE counts during microcrack expansion are nearly zero,and the intensity of the AE signal is extremely low(Fig.9i).It demonstrates that at-4°C-0°C,the expansion of a large number of microcracks releases less elastic energy.

3.3.2.Change of AE b value

To quantify the magnitude of seismicity,the G-R formula was used to express the statistical correlation between earthquake magnitude and frequency (Gutenberg and Richter,1944):

whereMis the magnitude,Nis the number of events for which the magnitude is higher thanM,andaandbare the constants.

The parametersbandahave specific physical significance.Thebvalue represents the ratio of small-magnitude events to largemagnitude ones.The destruction of a rock sample is comparable to a natural earthquake,with the exception of differences in magnitude and radiation frequency.Consequently,the relationship between the amplitude of an earthquake and its frequency can be utilized to analyze AE events during rock failure.Eq.(3)is expressed as follows (Colombo et al.,2003;Goebel et al.,2013):

whereAdBis the AE event amplitude,andN′is the hit number of AE events whose amplitude exceedsAdB.Thebvalue is used to analyze the variation in AE events and rock failure.This demonstrates that during rock failure,when microcrack propagation is dominant,higherb-values can be noticed;whereas macrocrack propagation occurs,bvalues fall (Colombo et al.,2003;Nejati and Ghazvinian,2013).

Fig.10 shows variation of the AEbvalue during thawing.The AEbvalue exhibits two stages with temperatures:basically unchanged and rapidly increasing.At-20°C to-4°C,the AEbvalues remain essentially unchanged,indicating that thawing has slight impact on the amplitude and number of AE events during the loading process.At-4°C-0°C,AEbvalues increase rapidly,indicating that the large amplitude AE events decrease while the small amplitude events rise.In other words,the microcrack propagation is more significant at-4°C-0°C.This is consistent with the results displayed in Fig.9.

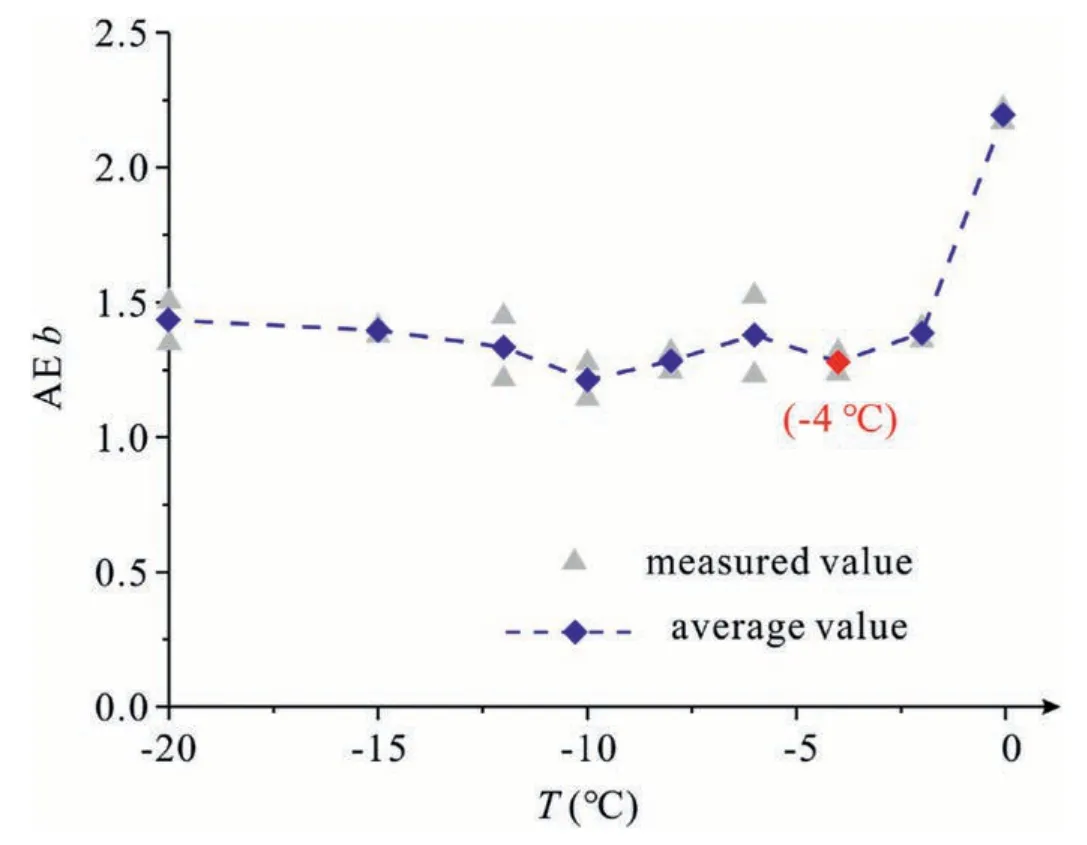
Fig.10.AE b-value at different thawing temperatures.

3.4.Variation of pore ice during thawing of frozen rock

The fracture behaviors of frozen rock are susceptible to temperature change,which should be attributed to thawing of the pore ice.Based on the principles in Section 2.3,the variation of pore ice content during thawing can be determined by subtracting the unfrozen water content from overall water content.

The variation of ice and unfrozen water content is shown in Fig.11.It shows that at-20°C to-4°C,the unfrozen water content gradually rises and the ice content decreases,indicating that a small amount of ice is melted.At-4°C-0°C,the unfrozen water content rapidly grows,and the ice content quickly decreases,showing that a lot of ice is melted.At 0°C,the ice content is zero,which suggests that the ice in the pores of frozen rock is completely melted.Coincidentally,the critical temperature for the variation of ice content is also -4°C,which may hold the interpretation of thawing-induced softening effects on the fracture behaviors of frozen rock.

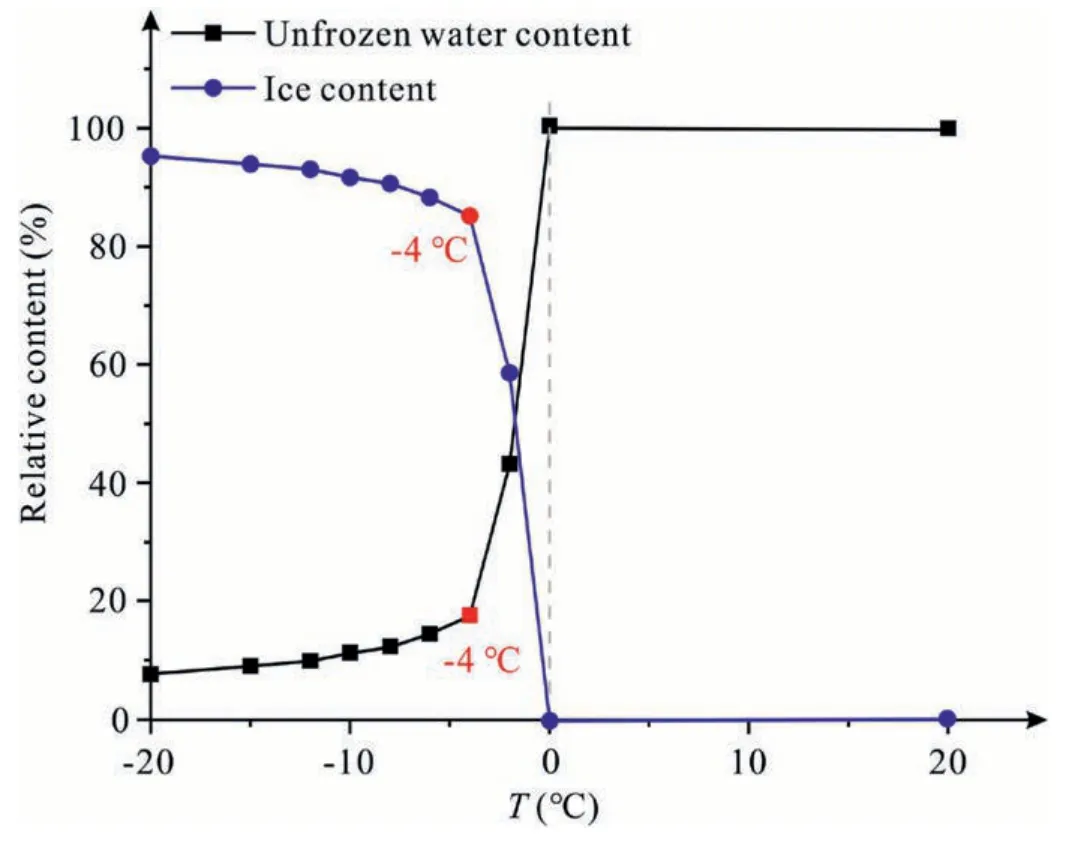
Fig.11.The relative unfrozen water content and ice content at varying thawing temperatures.

4.Discussion

Thawing can induce a significant softening effect on the fracture behaviors of frozen rock,which is evidenced by the decrease inKIC,fracture energy (Fig.5),and the increases in horizontal strain(Fig.6)and AE signals(Fig.9)with rising temperature from-20°C to 0°C.Moreover,-4°C is recognized as a critical temperature for the softening effect,where the softening effect intensifies (see Figs.5-8,10).Coincidentally,the NMR results demonstrate a reverse variation trend in pore ice content with increase of temperature,that is,a moderate decrease is followed by a sharp decrease and-4°C is exactly the critical point(Fig.11).Accordingly,we interpreted the thawing-induced softening effect by linking evolution in the microscopic structure of frozen rock with its macroscopic fracture behaviors.

When water-saturated rocks were frozen at -20°C,a vast majority of pore water was froze but the rest remained unfrozen in the form of a thin film between ice and mineral grains(Jia et al.,2019;Wang et al.,2022).Pore ice and unfrozen water film has two strengthening effects on the mineral skeleton (Wang et al.,2021):

(1) The filling effect of pore ice.A stress concentration effect will occur at a crack tip when the crack is under tension,leading to an increased stress.The stress concentration effect in the crack is positively correlated with its length-diameter ratio(Hertzberg,1996).The presence of ice drastically reduces the effective length of the crack (Fig.12,at -20°C),hence relieves the stress concentration effect at the crack tip.The filling effect depends on the pore ice content.

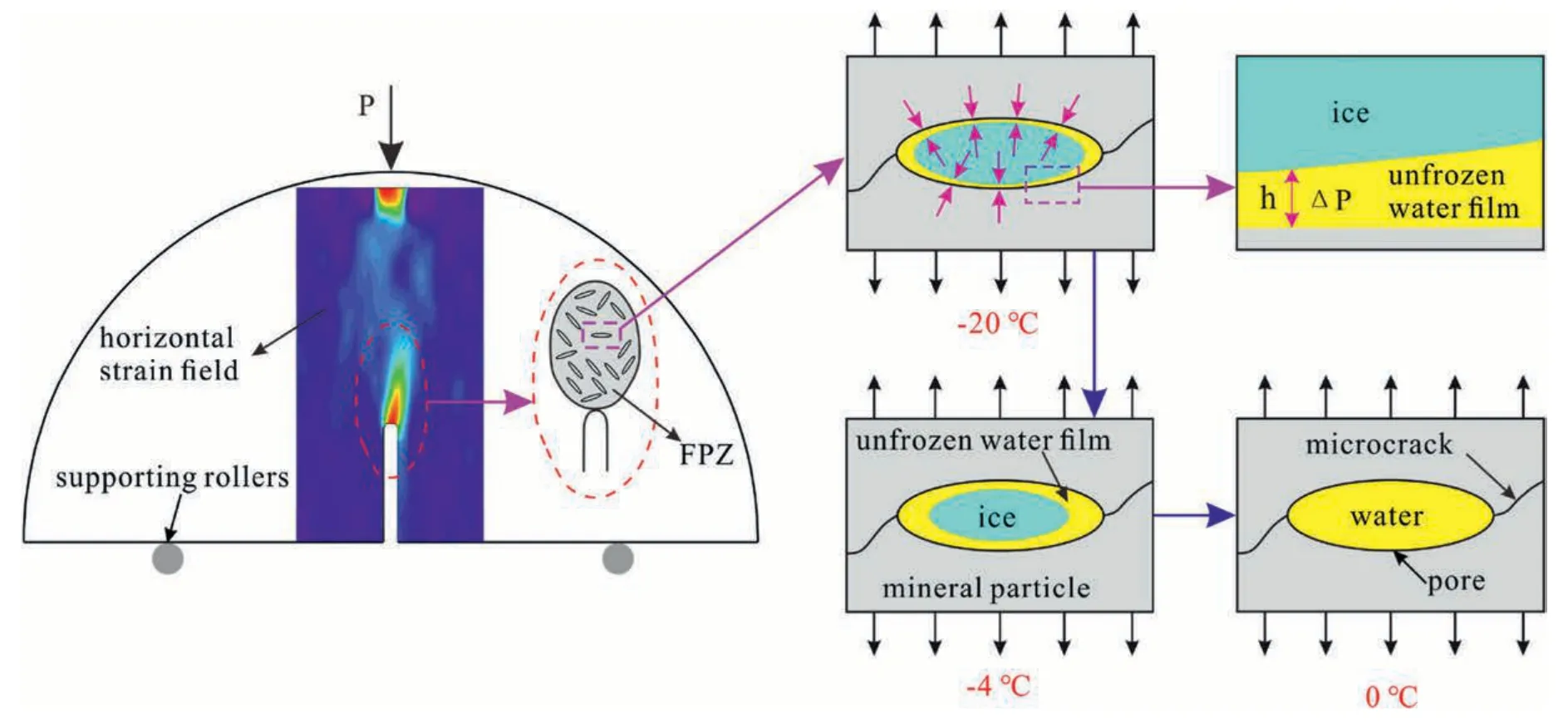
Fig.12.Influence mechanisms of thawing on fracture of frozen rock.

(2) The cementation effect of the unfrozen water film.The ice is cemented to the rock skeleton through the unfrozen water film (Fig.12,at -20°C),hence increasing the resistance to tension failure of the crack.The cementation effect is negatively related to the thickness of unfrozen water film,which depends on temperature (Guerin et al.,2016;Chen et al.,2018;Wang et al.,2021).The melting of ice within the cracks diminishes the two strengthening effects,resulting in a degradation of the fracture mechanical properties of frozen rock.

The melting of crack ice initiated from its outer boundary,i.e.the unfrozen water film.When the temperature increases from-20°C to-4°C,a small quantity of ice is melted,resulting in thickening of the unfrozen water film (Fig.12,at -4°C).So,the cementation strength between ice and rock skeleton decreases,making microcracks easier to propagate (Figs.6a-g and 7).This process also is responsible for the increase of FPZ length(see Fig.8),and the crack is more likely to fracture.However,as the above two strengthening effects are still significant,high-amplitude AE events dominate during the microcrack propagation process,and the AE signals are relatively strong(Figs.9a-g and 10).The weakening of the fracture mechanical parameters of frozen rocks during thawing is primarily determined by the thickness of the unfrozen water film within this temperature interval.

As temperature is greater than-4°C,much of the ice is melted(Fig.12,at 0°C),and the unfrozen water content rises rapidly(Fig.11b).As a result,the cementation effect of ice almost vanishes and the filling effect of pore ice is reduced significantly,facilitating the propagation of microcracks(Figs.6g-i and 7).In addition,due to the weakening of the two strengthening effects,small amplitude AE events dominate the microcrack expansion process,and the amplitude of AE signals decreases significantly (Figs.9g-i and 10).After the specimen is completely melted,both strengthening effects disappear,and the AE signals are very small (Fig.9i).

5.Conclusions

A series of SCB tests were conducted on frozen rocks at various thawing temperatures,and the microcrack propagation process was monitored by AE and DIC methods.By linking the evolution in microscopic structure of frozen rock with its macroscopic fracture behaviors,the influence mechanisms of thawing were interpreted.

(1) As the thawing temperature rises,the variation inKICof frozen rock exhibits a two-stage mode of slow decrease stage,KICdeclined by 19.5%from-20°C to-4°C;and rapid decrease,KICdeclined by 74%from-4°C to 0°C.The fracture energy varies in two stages: (a) essentially unchanged(-20°C～-12°C);and(b)rapidly decreased(-12°C-0°C).

(2) During the loading process,when the thawing temperature is at -20°C to-4°C,the HS at the notch tip varies in three stages:(I)changeless stage;(II)moderate increase stage;and(III) rapid increase stage,which correspond to the three stages: elastic deformation stage,microcrack propagation stage,and the microcrack coalescence stage.However,the change of HS at the notch tip shows a two-stage mode of(II)moderate increase stage and (III) rapid increase stage at -4°C-0°C,which corresponds to the microcrack propagation stage and microcrack coalescence stage.

(3) The microcrack propagation load,microcrack coalescence load,and macrocrack propagation load all decrease in two stages.At-20°C to-4°C,the microcrack propagation load is reduced to 0 kN,while the microcrack coalescence load and macrocrack propagation load are moderately decreased.At-4°C-0°C,the microcrack coalescence load and macrocrack propagation load fall rapidly,while the microcrack propagation load remains constant at 0 kN.Moreover,when the temperature increases,the FPZ length grows significantly.

(4) During fracturing of frozen rock,the AE counts change in three stages at -20°C to -4°C and in two stages at 0°C to-4°C,which is consistent with the variation of HS at the notch tip.The AE counts at 0°C to-4°C are much fewer than that at -20°C to -4°C.In addition,at -4°C-0°C,the microcrack propagation at the notch tip is more prominent than that at -20°C to-4°C.

(5) The weakening mechanism of the fracture mechanical parameters of frozen rocks differs at various thawing stages.At-20°C to-4°C,the thickening of the unfrozen water film diminishes the cementation strength between ice and rock skeleton,so the weakening of fracture mechanical parameters is primarily determined by the thickness of the unfrozen water film.However,at-4°C-0°C,the cementation effect of ice almost vanishes,and the filling effect of pore ice is reduced significantly,which facilitates microcrack propagation.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgments

We acknowledge the funding support from the National Natural Science Foundation of China (Grant No.42271148).