A Bayesian multi-model inference methodology for imprecise momentindependent global sensitivity analysis of rock structures
2024-03-25AkshayKumarGauravTiwari
Akshay Kumar,Gaurav Tiwari
Department of Civil Engineering, Indian Institute of Technology (IIT) Kanpur, Kanpur, 208016, India
Keywords: Bayesian inference Multi-model inference Statistical uncertainty Global sensitivity analysis (GSA) Borgonovo’s indices Limited data
ABSTRACT Traditional global sensitivity analysis (GSA) neglects the epistemic uncertainties associated with the probabilistic characteristics (i.e.type of distribution type and its parameters) of input rock properties emanating due to the small size of datasets while mapping the relative importance of properties to the model response.This paper proposes an augmented Bayesian multi-model inference (BMMI) coupled with GSA methodology(BMMI-GSA)to address this issue by estimating the imprecision in the momentindependent sensitivity indices of rock structures arising from the small size of input data.The methodology employs BMMI to quantify the epistemic uncertainties associated with model type and parameters of input properties.The estimated uncertainties are propagated in estimating imprecision in moment-independent Borgonovo’s indices by employing a reweighting approach on candidate probabilistic models.The proposed methodology is showcased for a rock slope prone to stress-controlled failure in the Himalayan region of India.The proposed methodology was superior to the conventional GSA (neglects all epistemic uncertainties) and Bayesian coupled GSA (B-GSA) (neglects model uncertainty) due to its capability to incorporate the uncertainties in both model type and parameters of properties.Imprecise Borgonovo’s indices estimated via proposed methodology provide the confidence intervals of the sensitivity indices instead of their fixed-point estimates,which makes the user more informed in the data collection efforts.Analyses performed with the varying sample sizes suggested that the uncertainties in sensitivity indices reduce significantly with the increasing sample sizes.The accurate importance ranking of properties was only possible via samples of large sizes.Further,the impact of the prior knowledge in terms of prior ranges and distributions was significant;hence,any related assumption should be made carefully.
1.Introduction
Sensitivity analysis is an important technique employed in rock mechanics to evaluate the relative importance of input properties for model response by estimating the resulting variation of the model response due to the variations of input properties(Fang and Su,2020;Xu et al.,2020;Pandit and Babu,2022).This assists the users in scheming the laboratory and field investigation in an efficient way by diverting major resources for the estimation of sensitive input properties.Additionally,sensitivity analysis helps reliability analysis become more computationally efficient by identifying which properties should be regarded as random variables or deterministic quantities (Pandit et al.,2019;Kumar and Tiwari,2022a).
Sensitivity analysis can be divided into two major classes: local sensitivity analysis (LSA) and global sensitivity analysis (GSA)(Borgonovo and Plischke,2016).LSA estimates the sensitivity by perturbating the input properties by small magnitudes close to their nominal values.Therefore,LSA fails to adequately explore the complete input space.LSA depends on the local gradient of the function in relation to the input properties,which leads to certain inherent constraints.LSA may lead to inaccurate results for any generic performance function(G(x))with(a)nonlinear nature and changing derivative point,and(b)interaction terms between input parameters (e.g.∂G/(∂xi∂xj)and ∂G/(∂xi∂xj∂xk)).GSA overcomes these limitations of LSA by estimating the input property’s global(complete input space) influence on the model response indicated by the changes in their probabilistic characteristics.Further,the GSA can consider the interaction effects between input properties.Hence,GSA is now widely applied across different engineering domains (Christen et al.,2017;Donaubauer and Hinrichsen,2018;Banyay et al.,2019)along with rock engineering(Pandit et al.,2019;Fang and Su,2020;Xu et al.,2020;Kumar and Tiwari,2022a;Pandit and Babu,2022).
Over the years,several GSA methods have been developed,with variance-based (i.e.Sobol’s) method emerging as the preferred choice among researchers.Sobol’s GSA is significantly superior to LSA as it performs well for nonlinear models,robust to model type and accounts for the probability density over a parameter domain(Saltelli et al.,2006).Because of these reasons,Sobol’s GSA has been used extensively in the rock mechanics domain in recent years(Pandit et al.,2019;Fang and Su,2020;Kumar and Tiwari,2022a;Pandit and Babu,2022).However,it should be noted that the variance is only a moment of the probability density function(PDF)which can provide only a summary of the distribution.This mapping of the entire distribution information to a single number leads to the inevitable loss of resolution (Helton and Davis,2003).Moment-independent GSA like Borgonovo’s GSA overcomes this limitation of Sobol’s GSA by considering the changes in the entire distribution in contrast to a particular moment,as shown in Fig.1.Limited studies are available on the applicability of Borgonovo’s moment-independent GSA for rock mechanics (Xu et al.,2020;Pandit et al.,2022) problems possibly due to its mathematical complexity.
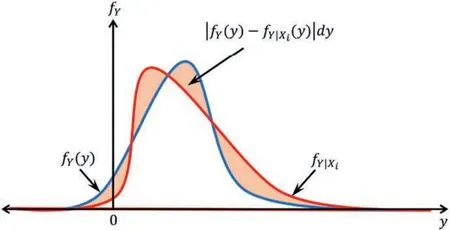
Fig.1.Illustration of the inner integral required for the estimation of Borgonovo’s moment-independent sensitivity indices.
The mathematical framework of the above-mentioned GSAs relies on the classical probability theory and requires probabilistic characteristics,i.e.distribution type and associated parameters of the input properties for the analysis (Borgonovo and Plischke,2016).Hence,the accuracy of GSAs relies upon the accurate estimation of the probabilistic characteristics of input,which in turn relies majorly upon the sufficiency of the investigation data.However,data for characterizing the input properties are more often very sparsely available for rock mechanics projects due to financial and practical difficulties in conducting tests,sample preparation,etc.(Wyllie and Mah,2004;Ramamurthy,2014;Pandit et al.,2019;Kumar and Tiwari,2022a,2022b).This epistemic uncertainty arising from limited data often compels to make subjective assumptions on the characteristics of input properties.This may further lead to inaccurate and non-conservative estimation of sensitivity indices(Zhang et al.,2021).Bayesian inference provides a coherent framework to account for the parameter uncertainty of a considered probability model (Ang and Tang,1975).It has been recently employed to deal with the uncertainties in the parameters of the probabilistic models used to represent the data of rock properties(Contreras et al.,2018;Bozorgzadeh and Harrison,2019;Contreras and Brown,2019;Aladejare and Idris,2020).However,the major issue with these studies is the ignorance of the uncertainties associated with selection of a probability model in the presence of limited data.In the presence of insufficient data,multiple models could statistically fit onto the available data with comparable accuracy.Traditional Bayesian analysis often ignores this issue by assuming a precise probability model to represent the data subjectively.Multi-model inference assists in overcoming this limitation of the traditional Bayesian methodology by considering the uncertainties in selecting the types of probability models(Burnham and Anderson,2004).Recently,some studies have considered this issue while performing the reliability analysis of geotechnical structures (Zhang et al.,2014;Wang et al.,2018;Li et al.,2019).Based on the literature review and to the author’s best knowledge,it was observed that no studies are available emphasizing the importance of data collection on the GSA.Some specific gaps can be identified as:(i)no studies on the inclusion of epistemic uncertainty (uncertainties in the model type and parameters) due to lack of data in the GSA of rock structures,(ii) no studies emphasizing the relative importance of uncertainties between model type and parameters on the imprecision of the estimated sensitivity indices,(iii)no studies on the effect of the sample size of properties on the imprecision in sensitivity indices,and(iv)limited studies on the applicability of moment-independent GSA for rock structures.
To address these issues,this study aims to propose a Bayesian multi-model inference (BMMI) coupled with GSA (BMMI-GSA),which infers the probability distributions of Borgonovo’s indices.BMMI was employed to characterize the uncertainties associated with model types and parameters of input parameters and propagated in the Borgonovo’s indices via Monte-Carlo Simulations(MCSs) and the model reweighting approach.Analysis of a slope along the jointed rock mass susceptible to stress-controlled failure is performed as an application example to demonstrate the proposed methodology,assessment of the confidence in the sensitivity indices and practical applicability in assessing the future investigation program to collect further data.The impact of sample size on the imprecision in the global sensitivity indices is also evaluated in depth.Further,analyses are also performed with traditional GSA(neglects uncertainties in model type and parameters) and conventional Bayesian coupled GSA (B-GSA) (neglects uncertainty in model types)to evaluate the relative significance of model type and parameter uncertainties on the sensitivity indices.The paper is structured as follows.Section 2 outlines the moment-independent Borgonovo’s GSA and explains its implementation algorithm in detail.Section 3 elaborates on the Bayesian and multi-model inference.Section 4 depicts the steps of RBF based response surface construction.Section 5 introduces the algorithm of the proposed BMMI-GSA methodology.Section 6 showcases its application in the sensitivity analysis of a rock slope.Section 7 provides discussions followed by the important conclusions in Section 8.
2.Moment-independent sensitivity methods
Moment-independent sensitivity methods,also referred to as density-based sensitivity methods,offer an alternative approach to evaluating sensitivity that considers the entire distribution rather than focusing on specific moments.This distinction prevents the loss of resolution encountered in moment-dependent methods,which summarize information into a single value (Helton and Davis,2003).The underlying concept of these methods is as follows:when all model inputs can vary according to their respective distributions,an unconditional model output density,denoted asfY(y),can be as illustrated in Fig.1.Additionally,by keeping the value of a particular model input(xi)fixed,a conditional density,denoted ascan obtain as shown in Fig.1.The sensitivity of the input variablexiis then evaluated based on the difference between the unconditional and conditional output densities,measured through methods like the Kullback-Leibler/Minkowski distance of order 2(Chun et al.,2000) or the area between these curves (Borgonovo,2007).To further generalize this approach,Borgonovo et al.(2016) proposed to incorporate the PDF or cumulative distribution function (CDF) of the output.This enables the utilization of different divergence measures,including the Kolmogorov-Smirnov statistic,absolute difference,or Kullback-Leibler divergence,to estimate the sensitivity measure ofxi.For our present study,Borgonovo’s moment-independent method was employed,which can be mathematically expressed in terms of the δ-sensitivity measure,serving as the first representative of the class of sensitivity measures:
This equation can be symmetrically represented as (Plischke et al.,2013):
where δisignifies the sensitivity measure ofxi;(xi)andfY(y)represent the PDFs ofxiandy,respectively;(y)is the conditional PDF ofy;andandDYrepresent the domains ofxiandy,respectively.Eqs.(1)and(2)are visually represented as the shaded area in Fig.1.
2.1.Estimating Borgonovo’s indices using the Monte Carlo method
In this work,Borgonovo’s analysis was performed via a histogram-based approximation based on Monte Carlo simulations(MCSs) due to its robustness and simplicity (Wei et al.,2013).This choice was taken in order to address the problem of biased inner integral estimate when utilizing kernel density estimators(Schmid et al.,2019;Antoniano-Villalobos et al.,2020).Further,the multimodel inference methods can be coupled conveniently with this analysis scheme for the imprecise sensitivity analysis proposed herein.The steps involved in the method are shown below.
Step 1.Generate a random realization x of sizeNfor input random vector X=(X1,X2,…,Xd)withdvariables based on their probability distributions:
Step 2.Evaluate the performance function(PF)G(∙)for the random realizations of x,i.e.y=(y1,y2,…,yN)=G(x(1),x(2),…,x(N))and estimate the unconditional PDFfY(y)via a histogram(normalized to give probability values)with a predefined number of binsnyas given below:
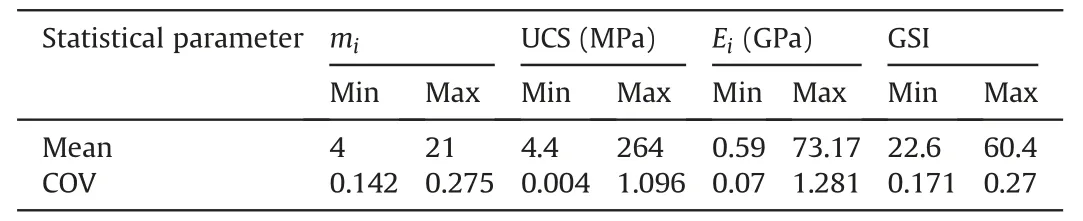
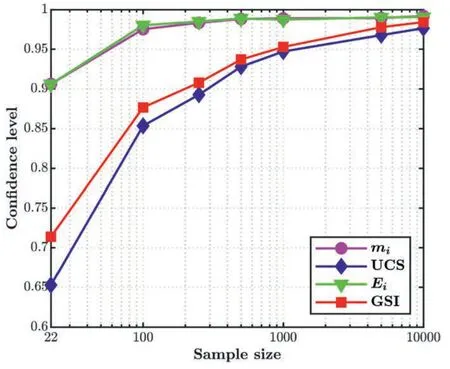
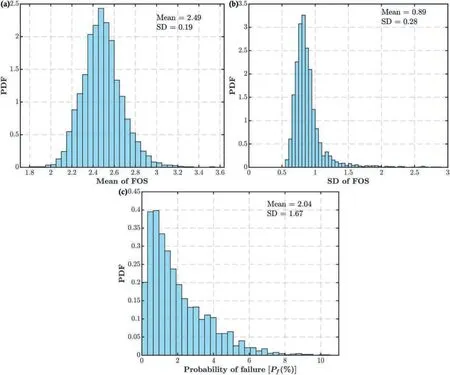
Step 3.Divide x=(x(1),x(2),…,x(N))intonxclasses(subsets) for input variableXiunder consideration.Each of thenxclasses ()could be defined by their bounds {lq,uq} withlq Step 4.Evaluate the PF values corresponding to each class,i.e.G(x(j)),x(j)∊and estimate the distribution ofYin each classvia the normalized histogram withnybins approximately as(y),t∊{1,2,…,ny}.Further,the conditional PDFcan be expressed approximately as given below: Step 5.Estimate the δiin accordance to the integral in Eq.(2) as given below: Step 6.Repeat Steps 3-5 for eachXi(i=1,2,…,d)and estimate the corresponding δi.The above algorithm is implemented in MATLAB. As mentioned previously,Borgonovo’s sensitivity method that requires the probability distributions of input properties must be precisely known.Samples are drawn from these known probability distributions of input properties to estimate their sensitivities.However,the precise characterization of probability distributions of input properties requires large data sets,which are seldom available for rock mechanics projects (Cai et al.,2004;Tiwari and Latha,2020).The major issue is related to the high costs and practical difficulties associated with the laboratory tests and in situ investigations (Duzgun et al.,2002;Wyllie and Mah,2004;Ramamurthy,2014).This section presents a Bayesian multi-model framework to quantify the uncertainties in the distribution type and its parameters emanating due to the limited sample sizes of properties.These uncertainties will be incorporated in Borgonovo’s sensitivity analysis to estimate the uncertainties in the sensitivity indices arising due to limited data which is discussed in Section 5. Bayesian inference allows to quantify uncertainties related to the parameters of a probability model (M).This method treats the model parameters (θ) to be random variables,and their prior knowledge is incorporated through the prior distributionp(θ;M).The posterior/updated distributionp(θ|D,M)) is obtained by combining thep(θ;M)with the site-data(D),which is described via a likelihood functionp(D|θ,M).Thep(θ|D,M)is mathematically expressed using Bayes’rule as shown below(Ang and Tang,1975): wherep(D;M)serves as the normalizing factor that ensures the integration of thep(θ|D,M)to unity and is defined as follows: Estimating thep(θ|D,M)often involves complex computations,particularly when analytical solutions are not readily available,except in cases where conjugate prior distributions are used.To address this computational complexity,this article adopts the Markov chain Monte Carlo (MCMC) simulation method.MCMC generates a sequence of random samples from thep(θ|D,M),significantly reducing the computational burden (Aladejare and Wang,2018;Liu et al.,2022). In Bayesian inference,an appropriate probability model of the property of interest is essential for the analysis.Common methods for selecting the probability model include statistical goodness-offit tests,Bayesian model selection,and information-theoretic based methods(Burnham and Anderson,2004;Zhang and Shields,2018).This article utilizes Bayesian information criterion(BIC)to estimate the best-fit probability model.BICrelies on the Bayes factors,which are ratios of integrated likelihood functions for different models.Mathematically,BICis expressed as follows: However,a major challenge arises when there are insufficient data (common in rock-related problems) to identify a best-fit probability model to be used in the traditional Bayesian inference analysis(Section 3.1).The Bayesian framework provides a means to quantify model uncertainty and assess the likelihood of candidate models accurately representing the dataset D (Burnham and Anderson,2004).The posterior probability ofMi,denoted aspi,can be calculated using Bayes’ rule: wherepiorp(Mi|D)represents the posterior probability andp(Mi)is the prior probability of modelMi.All candidate models are considered equally likely,with non-informative prior probabilities of modelsp(Mi)=1/Nd(i=1,2,…,Nd)in non-availability of prior information(Burnham and Anderson,2004). In the proposed multi-model inference (Burnham and Anderson,2004;Zhang and Shields,2018),all candidate models with non-negativepiare retained for the analysis,rather than focusing on a fixed best-fit model.The method ranks candidate models based on theirpivalues.BICcan be used to estimate thepiof each modelMiin the candidate set(Kass and Raftery,1995;Wit et al.,2012),where maximizingpicorresponds to minimizingBIC.Initially,theBICdifference valuesis estimated forMibased on itsBICvalue as given below(Burnham and Anderson,2004): whereBICminrepresents the minimum among the differentBIC(i)values of the candidate models M=(M1,M2,…,MNd).The best model emerges from this transformation with=0,whereas all other models have positive values.Thepican then be estimated by normalizing the likelihood exp(-/2)as follows: For non-informative prior probabilities of models,Eq.(10) reduces to Eq.(12) (Kass and Raftery,1995).The lesser theor larger thepi,the more likely it is that the modelMiin the candidate model set will accurately describe the provided data set.This ranking can be utilized to assess model uncertainty and prepare Monte Carlo simulation (MCS) sets required for later reliability analysis. This technique is used to generate samples for arbitrary probability models without relying on analytical density functions(Beck and Au,2002;Robert and Casella,2004).It proves to be a valuable tool in Bayesian inference,particularly for variables with complex posterior distributions that are challenging to express analytically.The MH algorithm was used as the MCMC method in this study since it is effective and easy to sample the posterior values of θ(Metropolis et al.,1953;Hastings,1970).For the MH algorithm to work effectively,careful consideration of the proposal distribution and initial value is necessary,as they have a significant impact on the Markov chain’s convergence to the stationary state.The initial samples are eliminated as burn-in because their validity may be in doubt depending on the initial value considered.Determining the optimal tuning parameter is essential and can be achieved by analyzing the trace plot (plotting Markov chain samples against sample numbers) and the autocorrelation plot (displaying the autocorrelation function(ACF)against lag values)of the simulated Markov chain samples (Roberts and Rosenthal,2001).A trace plot that resembles a hairy caterpillar shape with no anomalies,along with an autocorrelation plot showing a rapid and exponential decrease in correlation between samples,indicates that the chain has reached stationarity.Another numerical approach to assessing performance is through the acceptance rate.A 20%-40%acceptance rate is regarded as being efficient (Gelman et al.,1995).To ensure the successful execution of the MCMC sampling,a MATLAB subroutine was developed to produce random numbers from the posteriors. RSM constructs a surrogate prediction function for an implicit PF utilizing limited sampling points with known PF values.RBF-based RSM (RBF-RSM) are highly efficient for multi-variable and highly nonlinear PFs.RBF-RSM uses a series of linear combinations of radially symmetric functions to approximate the PF,which can be formulated as given below(Krishnamurthy,2003): where ‖X-Xi‖2depicts the Euclidian distance between observation or unknown point X andith sampling point Xi,and ψ represent the RBF.The quantity of training points generated via Latin hypercube sampling(LHS)is denoted byh,and λ=(λ1,λ2,…,λh)are the interpolation coefficients that need to be determined.These coefficients can be obtained by solving the system of linear equations: where Y=[G(Z1)G(Z2)…G(Zh)]Trepresents the estimated outputs athtraining points.A could be computed as follows: Classical RBFs are computationally inefficient when it comes to reproducing simple polynomials like constant,linear,and quadratic functions (Krishnamurthy,2003).To overcome this limitation,augmented RBFs are introduced,which can efficiently approximate simple polynomials.The augmented RBF can be expressed as(Krishnamurthy,2003): wherePj(X)represents the monomial terms of the polynomialP(X),andbjaremconstant coefficients corresponding to the polynomial augmented.For linear polynomials,m=d+1 (i.e.Pj(Z)=[1z1z2…zd]1×m),wheredis the degree of the polynomial.The additionalmcoefficients are estimated by employing the orthogonality condition: By combining Eqs.(14) and (17),λ and b can be estimated by solving the following equation: where Bij=Pj(Zi)fori=1,2,…,handj=1,2,…,mand b=[b1b2…bm]T. Commonly used RBFs ψ(∙)are linear,cubic,Gaussian and multiquadratic as given in Appendix A.In this study,the compactly supported RBF is employed,defined as wheret=r/r0andr0denotes the compact support radius of the domain,which can be estimated using the leave-one-out crossvalidation (LOOCV) method (Rippa,1999).Within LOOCV,a response surface is constructed usingh-1 sampling points,and cross-validation is performed on the left-out sampling point.The process of leaving out one sampling point is done for allhpoints.The cumulative squares of errors are computed for varying tuning parameters.Thetfor whichLOOCV(Eq.(20)) is minimum is used for the RBF response surface approximation. Furthermore,the accuracy of constructed RSM is evaluated by employing the Nash-Sutcliffe efficiency (NSE) as a measure of accuracy (Moriasi et al.,2007).To estimate NSE,additionalloffsampling points of inputs are generated.At these points,the FOSs are determined using both the RSMsand the original numerical programNSE can be computed as follows: whereG(X)meandenotes the mean value ofRSMs withNSE>0.75 is considered to have avery goodperformance rating.A MATLAB code was written to construct the RBF-RSM. The proposed BMMI-based GSA combines multi-model and Bayesian inferences to handle uncertainties due to the sparseness in data.This methodology aims to quantify uncertainties not only in the probability model type but also in the parameters of input properties.The process involves propagating these uncertainties through Borgonovo’s GSA to estimate imprecise sensitivity indices of rock properties.The overall methodology is depicted in Fig.2 to aid in comprehension.The steps involved in this approach are summarized as follows: Fig.2.Flowchart demonstrating the steps involved in the proposed BMMI-GSA for the estimation of imprecise sensitivity indices. (1) Step 1: Determination of properties.Determine the properties using standard methods (ISRM,1981). (2) Step 2: Define performance function (PF).Define the PF based on analytical or other methods.If an explicit PF is not available,the RBF-RSM can be utilized,as discussed in later sections. (3) Step 3: Identify plausible models and associated priors of model parameters.Initially select a candidate model set withNdmodels,i.e.M=(M1,M2,…,MNd)for all properties.Due to the non-negative nature of rock properties,the models defined for non-negative ranges were considered as the candidate models.Plausible models were selected from the candidate models with<10,since for>10,thepivalue almost becomes zero (Zhang and Shields,2018).The likelihood functionp(D|θ,Mi)corresponding to each plausible probability modelMifor a property with observation data D={D1.D2,…,Dn} can be formulated as below.Initially,select a candidate model set M=(M1,M2,…,)comprisingNdmodels,where each model corresponds to specific properties.As rock properties are non-negative,only models defined for non-negative ranges are considered as candidates.From this set,plausible models are identified based on a threshold of<10 (Zhang and Shields,2018). The likelihood function,p(D|θ,Mi),for each plausible probability modelMiassociated with a property and the observation data D={D1.D2,…,Dn} is formulated as follows: wherefrepresents the PDF value of theMievaluated at theq-th data pointDq,and θ denotes the parameters ofMi.The priors,i.e.p(θ;Mi),for all properties,are estimated using available data from literature. (4) Step 4: Evaluation of posteriorsp(θ|D,Mi).Employ Bayesian inference to estimate the posteriors of θ,i.e.i.e.p(θ|D,Mi),for each plausible modelMi,thereby quantifying their uncertainties.Analytical solutions forp(θ|D,Mi)involve computationally complex and inefficient multi-dimensional integration.To overcome this challenge,the MH-MCMC numerical sampling technique is utilized to generate a sequence of random samples fromp(θ|D,Mi)(Section 3.3). (5) Step 5: Estimation of imprecise Borgonovo’s sensitivity indices.Create a model set for each property,consisting of a large number (Nm) of models selected from the plausible models.Number of timesa model(Mi)is selected in the set ofNmmodels is determined,considering their correspondingpivalues (from Step 3) as weightage,i.e.=pi×Nm.Subsequently,values of parameters are selected at random from thep(θ|D,Mi)obtained in Step 4.Borgonovo’s sensitivity indices are then computed using the MCSs method by generatingNrandom realizations (Section 2)corresponding to each of theNmmodels in the established set.Statistics of the sensitivity indices,such as mean,coefficient of variation (COV),and PDFs,can be estimated to quantify uncertainties resulting from the small sample size. A MATLAB code has been developed to sequentially implement all the aforementioned steps to perform the imprecise GSA. This section demonstrates the proposed methodology by evaluating the sensitivities of strength and deformational properties of the rock along with the geological strength index (GSI) for the stability of a rock slope.Significant time,financial and human resources are required to estimate these properties.Data related to rock properties are often sparse in nature even for high-budget projects owing to the practical difficulties and significant dimensions of the project.It is therefore necessary to know the sensitivity of the individual rock property on the stability estimates of the slopes with poorly defined probability models characterizing input properties.Available resources can be optimally employed by investing more in the determination of those properties which are more sensitive to the stability estimates of the slope.Stability estimate of the slope is commonly defined in terms of the factor of safety (FOS)(i.e.PF),which is a function of rock properties. For this study,a Himalayan rock slope of dimension 293 m×196 m was selected.Main reason for this selection was the availability of the data required to demonstrate the methodology.This rock slope supports a railway bridge along a proposed railway line connecting Jammu to Srinagar.Dolomite with highly jointed and crossed by three major joint sets as well as a few more random joint sets makes up the lithology.The permeability at the location ranges from 0.48 to 70.48 Lugeons with closely spaced joint spacing and very tight apertures,respectively (Tiwari and Latha,2016,2019).Intact rock properties were estimated by standard laboratory tests on NX-sized rock cores collected from boreholes at intervals of 1.5-3 m.Laboratory testing of three to five samples of intact rock was conducted following the guidelines of the ISRM (1981).The rock was weathered to different degrees on the surface,while remaining fresh at greater depths.In some areas,the rock mass exhibited intense jointing,fracturing,and folding,with significant wrapping along the bedding joints and localized shearing (Tiwari and Latha,2016,2019,2020).Due to this complex geology (in terms of rock weathering,rock sample extraction depth,significant spatial extent of the site,etc.),significant range (variation) of the uniaxial compressive strength (UCS) was estimated.GSI was estimated using the traditional chart-based method and the correlation existing between rock mass rating (RMR) and GSI (Hoek and Brown,2019),i.e.GSI=-5,whereis the RMR value adjusted for groundwater rating and joint orientation.Table 1 summarizes the estimated data of the intact rock properties (i.e.mi=Hoek-Brown strength parameter andEi=elastic modulus of intact rock)and GSI(Tiwari and Latha,2019).Sensitivities of these properties were estimated for the FOS of the slope. Table 1 Original sample of intact rock properties,RMR and geological strength index(GSI). Performance function for the slope could be defined asG(X)=FOS(X)-1,where X is the vector of input properties.FOS of the slope is traditionally defined as the ratio of the resisting forces(or available strength) to the driving forces along the failure surface.FOS value of less than 1 indicates the failure of slope as the magnitude of the driving force exceeds the available strength.The PF becomes negative when the FOS falls below 1 which indicates slope failure.Probability of failure (Pf) was estimated as the percentage of random realizations for which FOS values were less than 1 to the total realizations.Probability of failure(Pf)was assessed by performing MCSs random realizations (S) and determining the count of realizations (Sf) in which the PF resulted in a negative value.ThePfcan be expressed mathematically as follows: For the analysis,the first step is to obtain an explicit function of FOS in terms of input properties under consideration.The slope was concluded to be prone to stress-controlled failures based on the siteobservation (small scale stress-controlled failures) and geological conditions,i.e.closely spaced joints as compared to the slope dimensions(Tiwari and Latha,2019).Derivation of an analytical and explicit PF for the slopes prone to these failures is difficult using the traditional Limit Equilibrium Method (LEM) due to the nonavailability of a clearly defined failure surface.RSMs coupled with numerical methods like the Finite Element Method (FEM) can provide a robust alternative to obtain an explicit surrogate expression of FOS in terms of the rock properties.RSM was constructed by generating realizations of input properties using LHS and estimating the corresponding FOS values via numerical simulation of the slope for these realizations. As mentioned in Section 4,the RBF-RSM was employed in this study to obtain a surrogate relation between FOS and input properties.A total ofh=100 random realizations of inputs were generated via LHS based on their statistics mentioned in Table 1.FOS values for these random realizations were obtained using an FEM-based program RS2 (https://www.rocscience.com/software/rs2).A typical RS2 model of the slope is shown in Fig.3.This program estimates the FOS using the shear strength reduction (SSR)method,which helped to overcome the limitations of LEM-like assumptions related to the shape of failure surfaces,slope geometry,constitutive models of rock,etc.(Kanungo et al.,2013).Rock mass was considered to exhibit elastic perfectly plastic behavior,with failure determined by the Hoek-Brown strength criterion.For each realization in the study,the rock mass properties necessary for RS2 modeling were acquired by using the GSI and intact rock properties,employing empirical relations (Hoek et al.,2002;Hoek and Diederichs,2006).Oncehsampling points of input properties,i.e.[X1,X2,…Xd]and output vector Y were known,the RBF-RSM was constructed by determining the coefficients λ and b as given in Section 4. Fig.3.Typical finite element model prepared in RS2 for the estimation of factor of safety (FOS) at the sampling points of input properties to construct the response surface. It should be noted that the RSM was constructed to obtain the FOS directly based on the intact rock properties(Ei,UCS andmi)and GSI(d=4 (Section 4)) instead of rock mass properties.This is due to two primary reasons: (i) objective of this study was to estimate the sensitivities of those properties which require significant laboratory and in situ resources for their determination,i.e.intact rock properties and GSI.Rock mass properties are simply determined using empirical relations between these properties only,and(ii)to decrease the computations required in the transformation of intact rock properties and GSI to rock mass properties for each realization in the sensitivity analysis.NSE of the RSM was 0.9681 (i.e.NSE >0.75) forl=50,which corresponds tovery goodrating.Therefore,the FOS for any new observation point X can be obtained using the constructed RBF-RSM. As mentioned earlier,data related to the rock properties are often sparse and hence,sensitivity analysis should be performed by considering the effect of poorly defined probability models of input properties.For the multi-model Bayesian analysis from the sparse data,basic inputs required are the candidate models and the priors of the associated model parameters.Candidate models formi,Ei,UCS and GSI were considered to be Rayleigh,lognormal,Weibull,gamma,inverse Gaussian,Nakagami and loglogistic due to their non-negative nature.Normal distribution was not considered as candidate model since it may give unrealistic negative values(Hoek,2007).Fig.4 shows the histogram with fitted candidate models for UCS and GSI.Plausible models(models to be considered for further analysis)were selected among the candidate models by estimating theBICorpifor the candidate models.Results are summarized in Table 2.The models with>10 orpi≈0 were considered to be the non-plausible models.It indicates that a nonplausible model has a significantly small probability of being the best-fit or representing the data sample appropriately.Multiple probability models were observed to be plausible for different properties.For example,all candidate probability models formiand UCS,and all candidate models except Rayleigh were plausible forEiand GSI with approximately similarBICorpi(i.e.minimalvalues).The result obtained supports the idea that it is unattainable to determine the best-fit model from a small size data sample. Table 2 Candidate probability distribution models and their corresponding BIC, BIC difference and BIC based probability pi values for mi,UCS, Ei and GSI. Table 2 Candidate probability distribution models and their corresponding BIC, BIC difference and BIC based probability pi values for mi,UCS, Ei and GSI. Note: Text in bold represents the candidate models with>10 or approximately zero pi values. Fig.4.Histogram of the original sample data with the candidate probability models for (a) UCS and (b) GSI. To reinforce this argument,pivalues for plausible models were estimated as a function of the sample size.Different sized samples(random realizations) were generated for different properties based on their best-fit models (i.e.with the lowestBICvalue).Results of a typical analysis for UCS are shown in Fig.5.Loglogistic model was the best-fit model for the UCS based on its original data.Samples of different sizes were generated andpivalues for plausible models were estimated.It was noted that till the sample size was suitably large (~1000),piof the Logistic distribution model was matching well with the other probable models.It is important to recognize that any analysis that assumes a single model as the best-fit for input based on sparse or limited data can be highly misleading. Fig.5.Variation of BIC based probability pi for the plausible models with the increasing sample size demonstrating the need of large sized samples to obtain the best-fit model for UCS with full certainty. Moreover,the priors of the model parameters were evaluated based on an extensive literature review.The review aimed to establish representative ranges of statistical moments for different properties.Aladejare and Wang(2017)provided the typical ranges of mean and COV for various rock properties based on a comprehensive analysis of 135 research articles from prominent journals,technical reports,and textbooks(Table 3).Moments were taken to be uniformly distributed between their identified bounds (Wang and Aladejare,2015,2016;Aladejare and Wang,2018;Liu et al.,2022).To estimate the priors of the model parameters,the correlations between these parameters and the statistical moments were utilized (Ang and Tang,1975).Table 4 summarizes the priors of the model parameters for different properties. Table 3 Prior information/knowledge for the sedimentary rock properties (Aladejare and Wang,2017). Table 4 Range of plausible model parameters to define the uniform prior for mi,UCS, Ei and GSI. In this step,thep(θ|D,Mi)for each plausible model were estimated using Bayesian inference,as explained earlier.The prior distributions were considered non-informative (uniform),i.e.p(θ;Mi)(Wang and Aladejare,2015,2016;Aladejare and Wang,2018;Liu et al.,2022).A total of 50,000 random realizations,by omitting the initial 5000 samples as burn-in to ensure convergence and efficiency,were generated.The convergence of the simulated chains was examined through trace and autocorrelation plots.The trace plots showed no anomalies,and the autocorrelation plots exhibited an exponential decrease between the sample correlations,indicating that the simulated values were not autocorrelated.Additionally,the acceptance rate of all Markov chains simulated for each model parameter fell within the desirable range of 20%-40%,indicating good quantitative performance.Fig.6 presents these plots for the Markov chain samples of the lognormal distribution parameters for UCS.The simulatedp(θ|D,Mi)for plausible UCS models are also shown as the joint PDF and the marginal PDFs in Fig.7 quantifying the uncertainties associated with them.Parameter values evaluated from the original data sample are shown as red dots along the joint PDF.The results highlight the presence of significant uncertainties in the model parameters due to the sparseness of the data. Fig.6.Convergence of the Markov chains as indicated by the(a)trace plot for parameter 1‘a’,(b)autocorrelation plot for parameter 1‘a’,(c)trace plot for parameter 2‘b’,and(d)autocorrelation plot for parameter 2 ‘b’ of the lognormal probability model for UCS. Fig.7.Marginal and joint PDFs of the posterior model parameters for the plausible models: (a) Lognormal,(b) Weibull,(c) Gamma,(d) Inverse Gaussian,(e) Nakagami,and (f)Loglogistic of UCS.Red points along the joint PDF show the parameter values estimated from the original sample. To estimate the imprecise sensitivity indices,plausible models along with their correspondingpivalues and posterior distributions of associated parameters were required.Using the plausible models and corresponding posterior parameters,a finite model set withNmmodels was first constructed for each rock property.Thepivalue of each plausible model served as a weighing factor,indicating the counts of the model to be included in the model set(pi×Nm).In this study,a total ofNm=5000 models of all properties were generated.Table 5 provides a summary of the count of each model was considered for different properties.For example,a model with apiof 0.016 (Rayleigh model formi) would be chosen 80 times(pi×Nm=0.016×5000=80)in the model set of 5000 models.For a model,its parameters were drawn randomly from the correspondingp(θ|D,Mi)obtained in the previous step.For the 5000 models,this process was repeated,resulting in 5000 models with randomly chosen parameters,as illustrated in Fig.8 for UCS and GSI. Table 5 Number of times a candidate model chosen to construct the finite model set for mi,UCS, Ei and GSI. Fig.8.Finite model sets with a total of 5000 models established for (a) UCS and (b) GSI for the BMMI-GSA. In the next step,a representative 5000 combinations of the probability models of different properties were chosen using the LHS.Each combination of the models involves a model of every property under consideration chosen from their generated models,as shown in Fig.8.Sensitivity indices(for such a combination)were estimated for different properties by generating theirN=105realizations and performing Borgonovo’s sensitivity analysis withnxandnybeing taken as 30 as mentioned in Section 2.1.Model evaluations required in Borgonovo’s analysis were performed using the RBF-RSM constructed for the slope in Section 4.The estimation of sensitivity indices is visually represented in Fig.9.Fig.9a shows the unconditional(blue color values)and conditional FOS values within a class (red color values) for the UCS value in the range [87.53-92.82].Corresponding unconditionaland conditionaldistribution(PDF)(via histograms)are shown in Fig.9b.The sum of the absolute differences between theandi.e.is representing the inner integral in Eq.(2).Results for a typical analysis in terms of the differences in the FOS distributions for different properties are shown in Fig.10.Values of the sum of absolute differences between theandfor UCS(0.6428)and GSI(0.8166)were found to be considerably greater in comparison tomi(0.1251)andEi(0.1779).This indicates the higher sensitivities of UCS and GSI for the FOS of the slope.This processmust be repeated for all representative combinations of the probability models resulting in 5000 values of sensitivity indices for all properties.Results of the analysis characterizing the imprecision in the sensitivities of the properties are shown in Fig.11 and Table 6. Fig.9.Typical representation of the estimated inner integral for the estimation of Borgonovo’s sensitivity indices conditioned on UCS:(a)Unconditional and conditional FOS values,and (b) Unconditional and conditional distribution (PDFs) of FOS for the UCS class defined in range [87.53-92.82]. Fig.11.Histograms and pair-wise joint PDFs of the Borgonovo’s sensitivity indices (δi) of rock properties (i.e. mi,UCS, Ei,and GSI) and Pearson’s linear correlation coefficients between them. BMMI-GSA provides the distributions/confidence intervals(CIs)of Borgonovo’s sensitivity indices instead of their single-point estimates,indicating the effect of uncertainties associated with sparse data of rock properties.It was observed that the UCS and GSI were more sensitive with their sensitivity indices ranging in the intervals (95% CI) [0.1958,0.543] and [0.116,0.4023],respectively.miandEishowed lesser sensitivities with sensitivity indices ranging in the interval [0.0251,0.1188] and [0.0298,0.1238],respectively.Properties can be broadly divided into two categories:(i) highly sensitive properties,i.e.UCS and GSI,and (ii) lesser sensitive properties,i.e.miandEi.Properties with higher sensitivities,i.e.UCS and GSI,have wider CIs compared to the lesser sensitive ones.However,the precise importance ranking of properties to ascertain the most sensitive property was not possible due to significant overlapping CIs of sensitivity indices.For the importance ranking of properties,samples of larger sizes were required for the GSA.An important observation was that the UCS is the most sensitive property based on the mean value of δi.However,the CIs of δishows that there is a probability of 16.67%that the UCS may not be the most sensitive input.Hence,the importance ranking provided based on the mean value of sensitivity indices could be misleading. Fig.11 also shows the histograms and pair-wise joint pdfs of sensitivity indices and Pearson’s correlation matrix.Results indicated a strong negative correlation (-0.88) between δUCSand δGSIsuggesting a possible negative linear relation between them,i.e.as the δUCSincreases,δGSIvalue tends to decrease,and vice versa.Also,a weak negative correlation was observed between δEiand δGSI(-0.13),indicating a slight tendency for these to move in opposite directions.However,no significant possibility of linear relationship was observed between other pairs of sensitivity indices(i.e.and δUCS(-0.05),and(-0.05),and δGSI(-0.06)and δUCSand(0.04)),as indicated by their negligible correlation coefficients. Furthermore,a convergence study was conducted to examine the impact of the sample size on the sensitivity indices.Samples of different sizes varying between 22 and 10,000 were generated based on the original sample data characteristics.Sensitivity analysis was performed for these sample sizes by employing the proposed BMMI-GSA methodology.Results are presented in Fig.12.UCS and GSI were significantly more sensitive as compared to themiandEiirrespective of the sample sizes.Further,the sensitivity indices of all properties converged within the sample size of 10,000.Convergence of the sensitivity indices of lesser sensitive properties was faster compared to the higher sensitive properties.This result can also be interpreted easily by plotting confidence level (CL) vs.number of sample points,as shown in Fig.13.TheCLuses the upper and lower bounds of CI,i.e.CIUandCILand can be defined asCL=1-(CIU-CIL)(Zhang et al.,2021).CL depends on the width of CI with higher values indicating lesser variation.It was observed that the imprecisions(variations)in the sensitivity indices for more sensitive properties(UCS and GSI)were higher as compared to the lesser sensitive properties (miandEi) for smaller data sets.This results in an important interpretation that the lesser (or more)sensitive properties can be grouped with the small sample size.However,it is difficult to perform the importance ranking precisely as convergence,especially for higher sensitive properties,isachievable for large sample sizes only.Based on the sample size of 10,000 importance ranking of the properties can be made as:UCS,GSI,miandEi. Fig.13.Variation of confidence level (CL) of Borgonovo’s sensitivity indices with the sample size of input properties indicating the faster convergence of sensitivity indices with increasing sample size for lesser sensitive properties and vice-versa. Further,the imprecise reliability analysis can also be carried out with the model set (consisting of 5000 models of every input)prepared for the imprecise sensitivity analysis as shown in Fig.8.For each of the 5000 model combinations of the model set,105random realizations were generated for each input based on the statistics and the model (for a particular model combination) and corresponding FOS values were obtained by performing MCSs on the prepared RBF-RSM using these realizations.Similar procedure was repeated for all combinations of the input models in the model set resulting in 5000 values of statistics of FOS as shown in Fig.14.For each model set combination,the realizations with FOS <1 could also be counted and divided by total realizations to estimate thePf.For 5000 model combinations (in the model set),5000 values ofPfcould be estimated as shown in Fig.14. Fig.14.Histograms of the (a) mean of FOS,(b) standard deviation (SD) of FOS,and (c) probability of failure (Pf). Determination of the rock properties requires significant financial and human resources,which is well documented in the literature(Duzgun et al.,2002;Wyllie and Mah,2004;Bozorgzadeh and Harrison,2019).The budget for the rock investigation program often lies in the range of 1%-5% of the total project cost,which is unjustified to characterize an inherently variable material like rock mass accurately.Hence,the limited data availability for rock mechanics projects is a serious and practical issue even for projects with high budgets.The condition becomes worse for low-budget projects where the investigation budget is limited (Sun et al.,2019;Spross et al.,2020).Due to these reasons,rock properties are often determined from the limited samples taken from the few boreholes and audits/drifts excavated along the selected locations of the site.Examples of high-budget projects are Chenab Railway Bridge and Kazunogawa hydropower projects (Cai et al.,2004;Tiwari and Latha,2020).For these projects,very limited(20-30)in situ plate load tests were conducted along the excavated drifts to determine the deformation modulus of the rock mass.Rock projects are often large-scale projects where engineers have to deal with natural material like rock mass with a formation history of thousand years.Hence,the rock mass is an inherently spatially variable material with the random presence of discontinuities of different features along it.Due to these reasons,any probabilistic characterization of the rock properties based on the limited test data collected from the specific locations is unreasonable.Traditional GSA ignores all these issues in the input data and estimates the sensitivities of the properties based on the best-fit probability model and the model parameters estimated from this limited investigation data.Traditional GSA assumes these probabilistic characteristics to be their ‘true estimates’ for the whole rock mass(i.e.population),which could be an unreasonable assumption and may lead to inaccuracies in the estimated sensitivities. The proposed BMMI-GSA addresses the limitations of traditional GSA methods by providing imprecise sensitivity indices instead of fixed-point estimates.This approach allows for representing the sensitivity indices as CIs and distributions,rather than a single fixed value that may not accurately reflect the true sensitivity of the properties.In practical applications,the true values of sensitivity indices are often unknown,and the traditional GSA cannot quantify the deviation of point estimates from these true values (so-called) (Zhang et al.,2021).In contrast,the interval estimates of sensitivity indices obtained through the proposed methodology offer lower and upper bounds in which the point estimates may range.These intervals include the true values of sensitivity indices at a fixed confidence level.Overall,the interval estimates of the sensitivity indices provide a more detailed description of the sensitivities of the properties.This makes the users more informed in making their decisions about planning the investigation program for a project.The user will remain informed to invest the resources in the determination of highly sensitive properties along with the required number of tests to reduce the imprecision to an acceptable level. BMMI-GSA provides a better alternative to the traditional GSA;however,some assumptions related to the input properties were made for the BMMI-GSA analysis of the application example.This section investigates the importance of these input characteristics on the overall analysis results so that the users should make more justified decisions in their selection.One key factor is the confidence of the prior information in the uncertainty characterization through the Bayesian inference (Cao et al.,2016;Wang and Akeju,2016;Liu et al.,2022) and their effect on the sensitivity analysis.A detailed analysis was performed to investigate this issue by varying(i)prior ranges and(ii)prior distributions of the statistics of properties.Ranges of the statistics were estimated based on the worldwide data available in the literature,with their prior distributions assumed to be uniform.The level of the information could be better in case the data are available from nearby sites with similar geological conditions instead of the worldwide collected data.Initially,the effect of the ranges of the statistics was estimated by narrowing down these ranges by approximately 60%,90% and 95% of the original range.These cases were named as Prior Knowledge II (PK-II),PK-III and PK-IV,respectively,while the original case was named as PK-I (in Section 6.3).Credibility (level)of the information could be arranged as: PK-IV >PK-III >PKII >PK-I.Prior distributions of properties were assumed to beuniform for all the cases (Fig.15a).Results are summarized in Fig.15b and c.With the increasing level of information,the imprecision in the sensitivity indices was continuously reduced,as indicated by the reducing width of the CIs.Minor changes(2.34%-24.33%) were observed in the CI width for PK-II case compared to PK-III and PK-IV cases with respect to the PK-I case. Fig.15.(a)Prior knowledge-I(PK-I),PK-II,PK-III and PK-IV with uniform distribution for mean of UCS;(b)CIs of Borgonovo’s sensitivity indices corresponding to PK-I,PK-II,PK-III and PK-IV with uniform distribution estimated from the BMMI-GSA;(c) Confidence level (CL) of Borgonovo’s sensitivity indices corresponding to PK-I,PK-II,PK-III and PK-IV with uniform distribution estimated from the BMMI-GSA;(d)PK-III with three prior distribution,uniform(U),normal(N)and Weibull(W)(i.e.PK-III-U,PK-III-N and PKIII-W) for mean of UCS;(e) CIs of Borgonovo’s sensitivity indices corresponding to PK-III-U,PK-III-N and PK-III-W estimated from the BMMI-GSA;and (f) CL of Borgonovo’s sensitivity indices corresponding to PK-III-U,PK-III-N and PK-III-W estimated from the BMMI-GSA. Additional analysis was performed by changing the prior distributions with the constant ranges of the statistics.Three distributions,i.e.uniform(U),normal(N)and Weibull(W),were selected corresponding to PK-III case(i.e.PK-III-U,PK-III-N and PK-III-W)for the analysis.Distributions were selected based on the literature as shown in Fig.15d(Liu et al.,2021).Fig.15e and f shows the results.The imprecision in the sensitivity indices was lower for Weibull and normal distributions as compared to the uniform distribution.This is indicated by the reduced CI widths of the sensitivity indices for these distributions (12.44%-37.01%) compared to the uniform distribution.Possible reason could be the less informative nature of the uniform distribution (also known as non-informative prior)with respect to the N/W distributions (Liu et al.,2021,2022). Further,two types of uncertainties related to input variables were considered in the BMMI-GSA: (i) model type,and (ii) model parameters.An analysis has been done to estimate the relative importance of these uncertainty types for the estimated sensitivity indices.Analysis was made by fixing the model type of the properties to their best-fit models with the lowestBICvalues (neglects model uncertainty).This analysis is called traditional Bayesian GSA(B-GSA).Posterior distributions quantifying the uncertainties of θ were estimated like the BMMI-GSA.The rest of the analysis was performed like the BMMI-GSA (except neglecting the model uncertainty).Table 7 summarizes the results of analysis.Mean sensitivity indices for all properties were matched for BMMI-GSA and B-GSA.However,the estimated COVs of the sensitivity indices from both methodologies were significantly different(percentage differences of 0.05%-45.6%).COVs of the indices estimated by the BMMI-GSA were higher as compared to the B-GSA analysis due to the incorporation of both model type and parameter uncertainties in BMMI-GSA.Further,this difference was higher for the lesser sensitive properties (i.e.miandEi) as compared to the highly sensitive properties (i.e.UCS and GSI).Overall,it was concluded that the model type uncertainties of input properties significantly affect the sensitivity indices and hence it should be incorporated in the analysis along with the uncertainties in model parameters. Table 7 Statistics of the Borgonovo’s sensitivity indices δi estimated through different methodologies. Rock engineering projects often suffer with the issue of limited data of rock properties due to many financial and resource constraints in the investigation program.Traditional GSA relies on this limited data to estimate probability models and associated parameters of input properties required to estimate sensitivity indices.This paper proposes a BMMI coupled with Borgonovo’s GSA methodology to estimate the imprecision in the momentindependent sensitivity indices of rock structures emanating due to samples of small size of rock properties.The proposed methodology estimates the uncertainties in the probability models and associated parameters of the input properties using BMMI.These uncertainties are propagated via MCSs and reweighting approaches to estimate the imprecision in the moment-independent Borgonovo’s sensitivity indices.Methodology was demonstrated for a Himalayan rock slope in detail and various aspects of imprecise sensitivity analysis were discussed.Sensitivity indices were represented in the form of CIs/distributions by this methodology instead of their point estimates estimated from a traditional GSA.These CIs assist the engineers in making a more informed decision on the sensitivities of properties and in planning the investigation program accordingly.In terms of the FOS of the slope,UCS and GSI displayed a considerably higher level of sensitivity compared tomiandEi.This observation could be made with the limited size of samples due to significantly different CIs of UCS and GSI as compared tomiandEi.However,significantly larger sized samples of properties were required to obtain converged sensitivity indices for the accurate importance ranking of the properties with overlapping CIs.Imprecision in the sensitivity indices was reduced with the increasing sample size with a faster convergence rate for lesser sensitive properties (miandEi).Prior ranges and the distributions associated with the prior information significantly affected the imprecision in the sensitivity indices.Uncertainties in prior information were observed to be directly proportional to the estimated imprecision in the sensitivity indices.More confident prior information from the nearby sites as compared to the worldwide data can significantly reduce the imprecision in the sensitivity indices.Further,the impact of the model type uncertainties of the properties on the estimated imprecision in the sensitivity indices was relatively lower as compared to the uncertainties in the model parameters. The proposed methodology is generalized in a way to employ it for a variety of problems.However,some inherent limitations of this methodology exist and should be addressed in follow-up research: (1) This study neglects the correlation between inputs while estimating the sensitivity indices. (2) Transformational uncertainties associated with the GSIbased empirical relations relating intact and rock mass properties were not considered. (3) Applicability of the proposed methodology should be evaluated for different types of problems. (4) Applicability of non-parametric densities in modeling the possible distributions of inputs (instead of parametric densities)could be investigated.Certain points need to be taken into care including overfitting of density estimation and the accuracy of smoothing parameter estimation for small size sample data. Declaration of competing interest The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper. Acknowledgments This work was financially supported with the initiation grant funded by Indian Institute of Technology (IIT) Kanpur. Appendix A.Supplementary data Supplementary data to this article can be found online at https://doi.org/10.1016/j.jrmge.2023.08.011.3.Bayesian multi-model inference for uncertainty estimation due to limited data
3.1.Bayesian inference to estimate parameter uncertainty
3.2.Multi-model inference to estimate model uncertainty
3.3.Metropolis-Hastings (MH) MCMC sampling
4.Radial basis function-response surface method (RBF-RSM)
5.Methodology

6.Application example
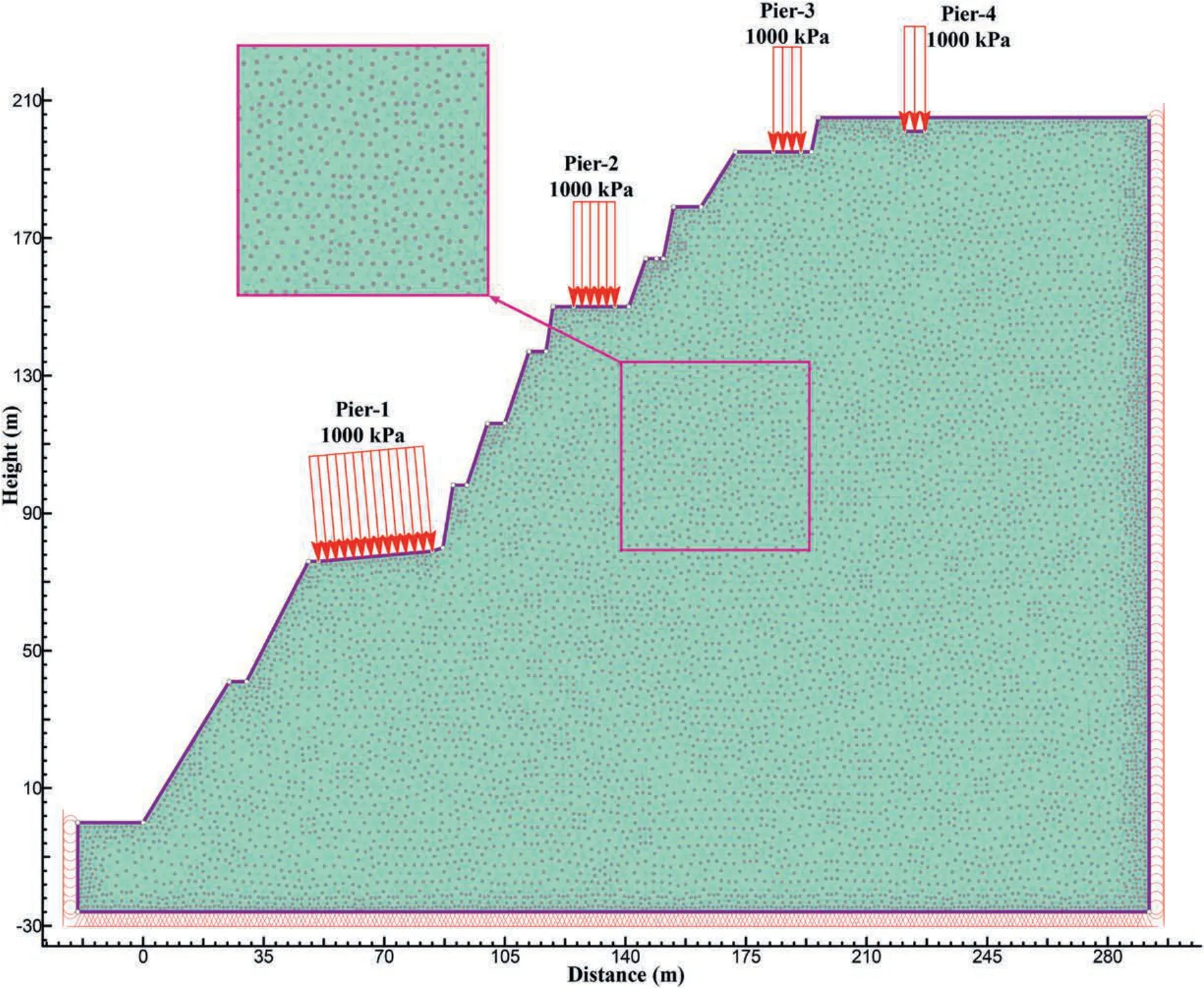
6.1.Problem description

6.2.Define performance function (PF)
6.3.Identification of plausible models and associated priors of model parameters




6.4.Evaluation of posteriors p(θ|D,Mi)


6.5.Estimation of imprecise sensitivity indices




7.Discussion


8.Conclusions and future work
杂志排行
Journal of Rock Mechanics and Geotechnical Engineering的其它文章
- Using deep neural networks coupled with principal component analysis for ore production forecasting at open-pit mines
- Sliding behaviors of the trapezoidal roof rock block under a lateral dynamic disturbance
- Real-time arrival picking of rock microfracture signals based on convolutional-recurrent neural network and its engineering application
- Failure characterization of fully grouted rock bolts under triaxial testing
- Nonlinear constitutive models of rock structural plane and their applications
- Mechanical behaviors of backfill-rock composites:Physical shear test and back-analysis
