EMCA:一种新的多云存储中高效的多副本审计方案
2024-03-25胡雨晴
胡雨晴,金 瑜
(1.武汉科技大学 计算机科学与技术学院,湖北 武汉 430065;2.湖北省智能信息处理与实时工业重点实验室,湖北 武汉 430065)
0 引 言
近年来,云存储[1]得到了广泛应用,它允许用户将其海量本地数据,以低廉的价格外包给远程存储服务器。然而,云存储也存在缺点:一旦用户将其数据外包给不可靠的远程存储服务器,且没有完整的本地备份,用户的数据就会面临许多安全威胁,例如,远程存储服务器会因为自然或人为事故、黑客攻击丢失数据,甚至会为了减少维护费用,故意删除用户很少使用的数据等等。学术界和工业界已经为解决这个问题付出了大量努力。云数据审计也称为可证明数据占有(Provable Data Possession,PDP)[2],是数据所有者在不下载数据的情况下检查数据是否在远程云服务器上正确存储的一项重要技术[3]。
尽管PDP可以帮助数据所有者检查数据完整性,但是一旦数据被破坏,数据所有者也会永远丢失数据。为了提高数据的持久性和可用性,数据所有者可以生成多个副本,如果一个副本被篡改,数据所有者可以利用其他副本恢复数据。然而,大多数现有方案只考虑检查单个数据的完整性[4-5],对于多个副本,必须运行N次以检查N个副本的完整性,这种方案的效率很低。为了克服这个问题,已有学者提出了一些用于多副本的PDP方案[6-7],而上述方案都只考虑了一个简单的情况,即所有副本都存储在一个云存储服务器上,一旦服务器出现故障,用户仍然面临数据丢失的风险。且传统的仅限于单一提供商数据中心的云基础设施正在不断发展,多云是下一代云系统的趋势[8]。因此,设计一种高效的多副本、多云存储服务器PDP方案是很有意义的。
根据上述多副本方案存在的问题,该文提出了EMCA(Efficient Multi-replica and multi-Cloud Audit),一种新的高效的多副本、多云数据审计方案。EMCA具有以下特性:(1)为多云存储服务提出了一个安全的数据审计方案,使用第三方审计者(Third Party Auditor,TPA)协助审计,实现了多云情景下的数据完整性验证。(2)能够一次验证不同云服务器上的所有抽样副本,采用模幂加密技术[9]计算审计结果,实现了高效的多副本批量数据审计。
1 相关工作
1.1 单副本数据审计
Ateniese等人[2]首次提出了PDP的概念,该方案利用基于RSA(Rivest-Shamir-Adleman)的同态验证标签(Homomorphic Verifiable Tag,HVT),将生成的标签聚合为单个值,大大减少了审计过程中的存储和通信开销。然而,该方案仅适用于验证静态文件。Erway等人[10]扩展了PDP模型,并首次提出了一种完全动态的PDP解决方案,称为DPDP,然而,该方案的执行效率仍然存在疑问。Wang等人[11]设计了另一种动态PDP方法,使用Merkle哈希树(Merkle Hash Tree,MHT)支持数据更新。此外,Zhu等人[12]使用索引哈希表(Index Hash Table,IHT)实现了全数据动态的公共审计,大大降低了计算和通信成本。
为了有效支持用户撤销,Wang等人[13]提出了Panda,通过使用代理重签名技术,半可信云服务提供商可以将被撤销用户生成的签名转移到目标用户私钥下。为了实现用户身份的隐私性,Wang等人[14]提出了第一个针对共享数据的隐私保护公共审计方案,称为Oruta。此方案将环签名和HVT相结合,对被质询块的签名进行聚合,实现了签名者身份保密的目的。此外,Shen等人[15]提出了一种基于身份加密的数据共享方案,简化了复杂的证书管理。
1.2 多副本数据审计
Curtmola等人[16]提出了一种基于RSA签名的多副本审计方案,这是首次尝试创建多个副本并对其进行检查的方案。通过先加密然后随机化来生成文件的多个副本,已实现副本的可区分性以及数据隐私。针对证书管理开销,Zhou等人[17]提出了一个无证书的多副本动态完整性审计方案,通过改进经典MHT实现副本的批量更新,同时提供可变副本数存储。然而,该方案并不支持多云环境。为了解决这个问题,不少学者提出了多云多副本的审计方案[18-19]。Yang等人[20]提出使用区块链中随机数的不可预测性来抵制恶意审计员,使用动态哈希表实现多云多副本的审计方案。然而,上述方案[18-20]均采用计算复杂的双线性配对完成完整性验证,导致计算成本较高。
基于此,设计一种在多云环境中高效的多副本数据审计方案是很有意义的。该文通过使用模幂加密技术来实现审计,其中最复杂的运算是模幂运算,这只会消耗很少的计算成本,同时,可一次验证不同云服务器上的所有副本,实现高效的多云多副本审计。
2 具体方案
2.1 预备知识
2.1.1 同态验证标签
数据块的同态可验证标签是一种不可伪造的验证元数据,它具有同态的特征,这是由Ateniese等人首次引入的。HVT的特性如下:
(1)无块验证。通过使用HVT,用户可以在不访问数据块的情况下验证CSP生成的完整性证明。
(2)同态标签。对于任意两个数据块bi和bj以及相应的同态验证标签Tag(bi)和Tag(bj),(bi+bj)的HVT可以通过Tag(bi)和Tag(bj)生成。
该文使用以下基于RSA的安全哈希函数来构造HVT。N=pq是一个公共RSA模,其中p=2p'+1和q=2q'+1是两个足够大的秘密素数。让QRN为模N的二次剩余集,g为QRN的生成元。因此,数据块bi的基于RSA的HVT可以定义为:
Tag(bi)=gbimodN
(1)
HVT的同态特性由以下等式给出:
Tag(bi+bj)=gbi+bjmodN=
(gbimodN)*(gbjmodN)=
Tag(bi)*Tag(bj)
(2)
另外,如果r和bi是两个足够大的整数,可以构造以下等式,该等式将用于后续的完整性验证:
Tag(bi)s=(gbi)smodN=gsbimodN=
(gs)bimodN
(3)
2.1.2 副本记录表
如表1所示,副本记录表[20]记录了文件副本与物理存储位置的映射关系。表项为文件号、副本号和CSPID,根据文件号和副本号可锁定唯一副本,根据CSPID可确定该副本的存储位置。其中,xi表示存储ID(F)第i个副本的CSP的ID。
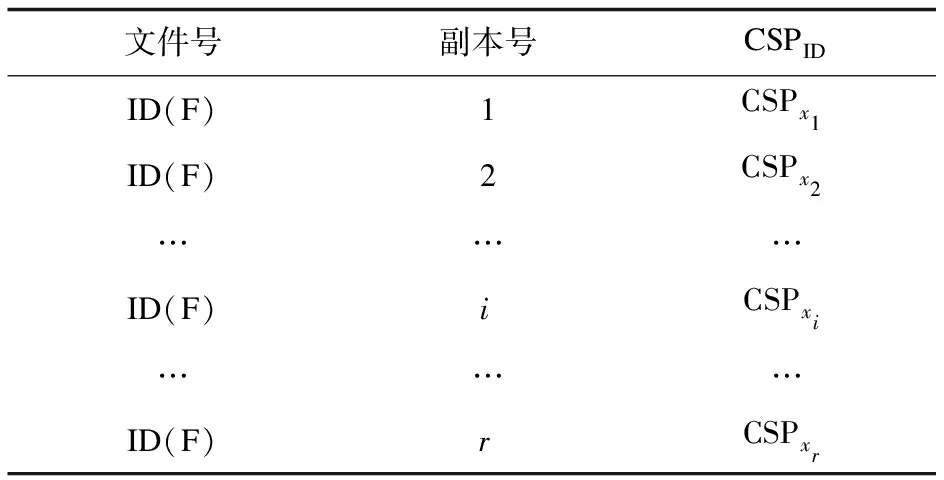
表1 副本记录表
2.2 系统模型
多云多副本的审计系统模型如图1所示,系统中包含四个实体:用户(User)、云服务提供商(Cloud Service Provider,CSP)、云服务管理者(Cloud Service Organizer,CSO)和第三方审计者(Third Party Auditor,TPA)。

图1 系统结构
用户(User)可以是个人或企业,它将数据存储在多个CSP上,还将检查外包数据的完整性。
云服务提供商(CSP)为用户提供网络存储和计算服务,但CSP可能会丢失或损坏用户数据。
云服务管理者(CSO)是一家特殊的云服务提供商,负责在多云环境下管理多个CSP。
第三方审计者(TPA)在用户的授权下管理或监控外包数据。
方案的大致过程如下:
(1)用户对数据进行初始化,将文件分块,并生成副本,将副本发送至CSP存储。
(2)用户生成数据标签并发送至TPA存储。
(3)CSP验证收到的数据是否正确。
(4)用户生成随机数,发送给TPA。
(5)TPA生成挑战信息并发送给CSO。
(6)CSO将挑战信息分派给CSP,CSPi生成证据Proofi,CSO将证据聚合成ProofCSP,并发送给TPA。
(7)TPA收到证据后,根据存储的标签计算ProofTPA。TPA将ProofCSP和ProofTPA一同发送给用户。
(8)用户利用第四步生成的随机数审计证据。
2.3 安全性假设
假设用户和CSO是可信的。
假设CSP是半可信的,恶意或粗心大意的CSP可能会丢失数据,也可能会删除用户很少使用的数据以减轻其存储负担。
假设TPA是半可信的。TPA可能通过与云服务器串通向用户隐瞒数据损坏事件。
2.4 关键过程
多云多副本的审计系统方案由三部分组成:初始化阶段、设置阶段和公开审计阶段。一些必要的符号定义如表2所示。

表2 相关符号定义
文中的一些密码变换如下(以k表示密钥长度):
E(·):{0,1}k×{0,1}*->{0,1}k为对称加密算法,用户对文件进行加密,如AES。
H(·):{0,1}*->Zp为普通无密钥Hash函数,如SHA-256。
2.4.1 初始化阶段
选择两个足够大的素数p和q来生成RSA模N=pq,并生成QRN的生成元g,将g,N公开。
用户发送ID给密钥生成中心,密钥生成中心选择两个随机数α∈Zp,β∈Zp,计算用户私钥(ssk)并将其发送给用户保存,ssk计算如式4所示:
ssk=α+βH(ID)
(4)
2.4.2 设置阶段
在设置阶段,用户将文件数据分块,并生成各数据块副本及标签,将副本发送给CSP存储,标签发送至TPA中存储,CSP确认数据一致无误后,用户可删除本地文件。设置阶段的具体流程如下:
(1)ReplicaGen:为了减少验证开销并适应多云存储的分布式环境,用户将文件F分成n块,F={b1,b2,…,bn},bi可以看作是一个足够大的整数。为得到r个副本,用户使用对称加密算法对原始数据块加密bij=Ek(i‖j‖bj),其中i=1,2,…,r,j=1,2,…,n,第i个副本Fi={bi1,bi2,…,bin}。同样,用户使用密钥k可对bij进行解密得到原始数据块bj。用户对加密数据块计算R如式5所示,随后用户将r个副本文件{F1,F2,…,Fr}以及R发送给CSP存储。
(5)
(2)TagGen:对于r×n个副本数据块,用户计算每个数据块的标签Tagij如式6所示,其中i=1,2,…,r,j=1,2,…,n。Tagi={Tagi1,Tagi2,…,Tagin},用户将r个副本标签{Tag1,Tag2,…,Tagr}发送给TPA存储。
Tagij=gbij*sskmodN
(6)
(3)CSP confirm data:CSP收到用户发送的数据后,计算以下等式是否成立:
(7)
若相等,则确认数据无误;否则,它将表明数据存在问题。此时,CSP将拒绝确认数据,并终止存储服务。此时用户并未删除本地文件,所以用户不会遭受任何损失。如果CSP确认所有数据无误,服务顺利进行,用户将删除本地文件。同时,CSO在副本记录表中记录副本的存储地址。
2.4.3 公开审计阶段
在公开审计阶段,用户检查多云存储服务,以确保外包数据安全存储在CSP中。为了减少开销,用户将批量审计部分副本数据块,以概率性检测检查整个外包数据的完整性。具体审计流程如下:
(1)ChalGen:用户秘密生成一个足够大的随机数s,计算挑战chal并将其发送给TPA。挑战chal的计算如式8所示:
chal=gsmodN
(8)
(2)SendChallenge:TPA收到用户发送过来的chal后,生成随机序列I和二维数组C:
(9)
I表示e个待审计的数据块编号序列,C表示对应e个待审计数据块及r个副本的r×e个系数。TPA将{chal,I,C}发送给CSO,等待CSO返回证据。
(3)ProofCSPGen:CSO分派挑战,各CSP计算证据返回,CSO聚合证据返回。具体步骤如下:
(a)CSO收到TPA发送过来的审计请求后,查询副本记录表找出存储了待审计副本的CSP,将对应的{I,Ct,chal}分别发送给对应CSP。
(b)CSP收到CSO发送的I={1,3,…,j},Ct={ct1,ct2,…,cte}与chal后,计算其存储的副本Ft的完整性证明prooft并将其发送给CSO,prooft的计算如式10所示。
(10)
(c)所有CSP返回证据后,CSO聚合证据计算proofCSP如式11所示,其中r为副本个数,CSO将Hash(proofCSP)返回给TPA。
(11)
ProofCSPGen算法流程如下所示:
算法1:ProofCSPGen()
输入:chal,I,C,{F1,F2,…,Fr}
输出:Hash(proofCSP)
(1)CSO从副本记录表中找到存储了待审计副本的r个CSPid
(2)fortin range(1,r)
(3)CSPt←{I,Ct,chal}
(4)foriin range(1,e)
(5)proofi←chalctibtlimodN
(7)return Hash(proofCSP)
(4)ProofTPAGen:在CSO计算审计证据时,TPA同时依据存储的标签以及待审计数据块编号序列I,和系数数组C计算proofTPA如式12所示,TPA返回证据{Hash(proofCSP),proofTPA}给User。
(12)
(5)Audit:用户收到TPA返回的证据后,根据用户秘密保存的随机数s以及ssk计算等式13是否成立。若成立,则用户认为CSP完好地存储了数据;否则,认为TPA或CSP是恶意的,存储在CSP中的数据可能遭到了损坏。
(13)
3 安全性分析
根据上述安全性假设,假定用户和CSO是可信的,他们会诚实地执行审计步骤,TPA和CSP是半可信的。在这种背景下,理论上分析所提方法的安全性。
在文中方案,有以下两种可能恶意破坏公平的云存储服务的行为:(1)CSP存储的数据丢失,试图使用伪造的证明通过验证;(2)CSP串通TPA伪造证明试图通过验证。
定理1(正确性):如果CSP和TPA都诚实地遵守规定的程序,那么证据可以通过User的验证。
证明:以下等式通过从左到右的推导,证明了Audit算法中的等式是正确的。
(14)
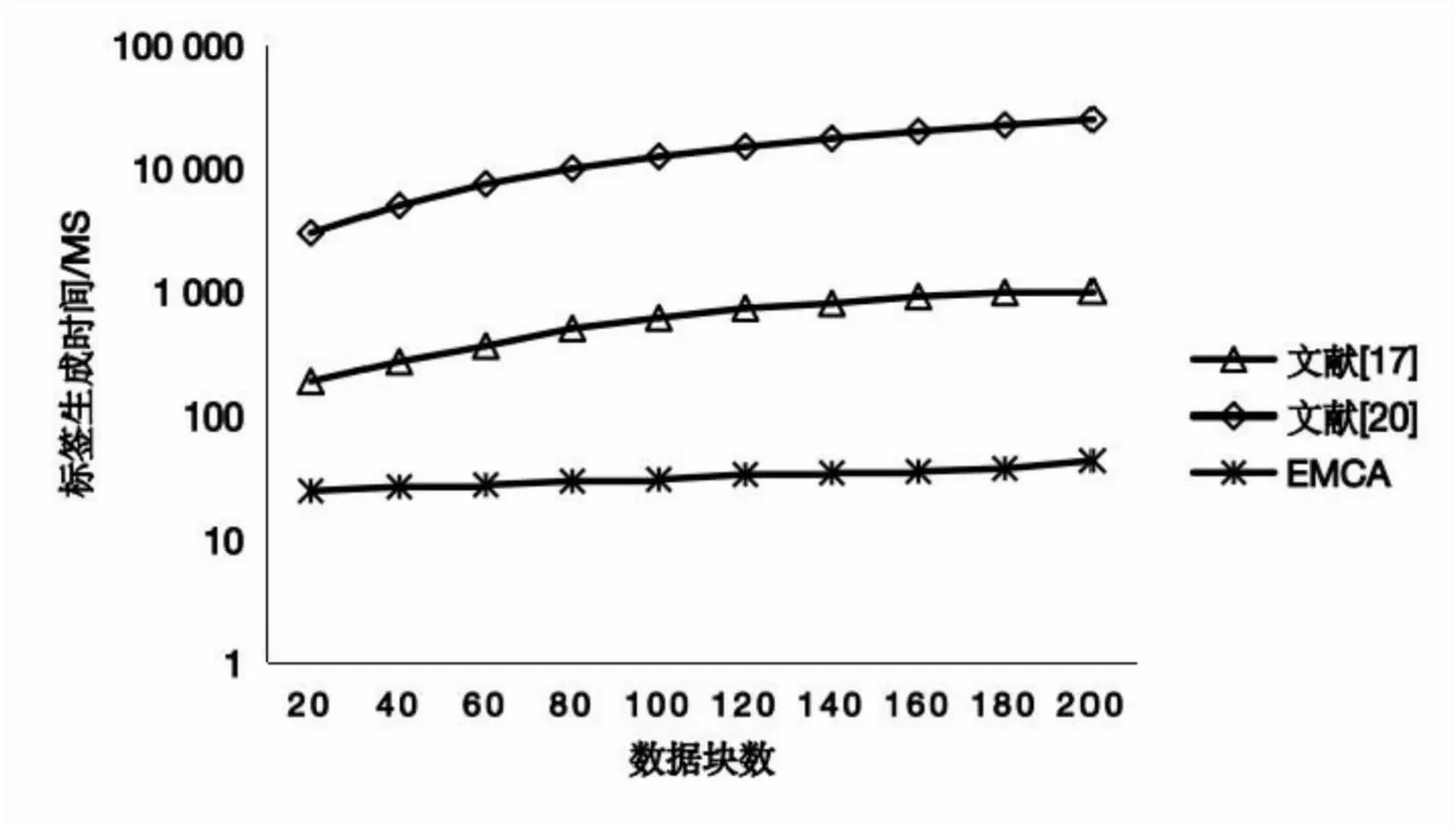
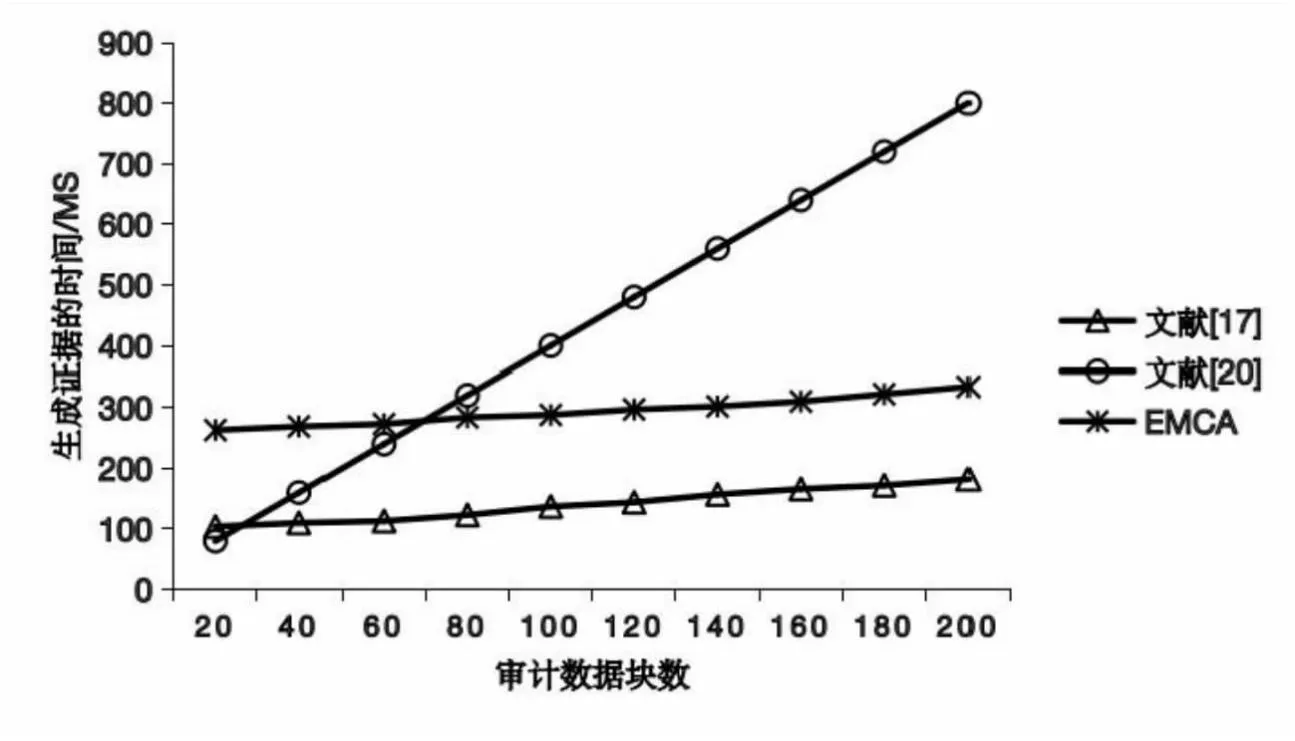
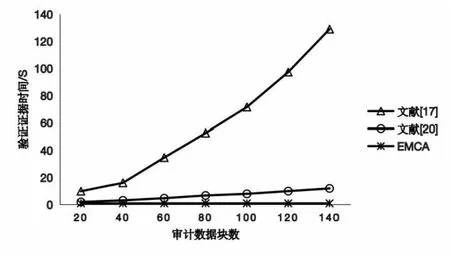
假设1(二次剩余问题):给定一个整数N=p×q,其中p和q是机密的,并且整数g 根据假设1,推导出定理2: 定理2:对于已知g,gsmodN和N的敌手,没有多项式时间算法可以找到任何满足s'≠s,N|gs-gs'的s'。 证明:假设存在多项式时间算法A1,对于给定s,g和N=p×q,总能找到一个s'满足s'≠s,N|gs-gs′,得到以下等式: s≡s'modord(g) (15) 其中,ord(g)是满足N|gord(g)-1的最小正整数,并且是一个真值与s-s'|ord(g)相同的奇数。若给定g可以满足ord(g)mod2=1,可以得到以下等式: gord(g)+1≡g(modN) (16) 相应的,也可以得到以下等式: (17) x2≡g(modN) (18) 如上所示,在算法A1的帮助下,可以生成一个多项式时间算法A2来找出满足x2≡g(modN)的x,而它与假设1相矛盾,由此,定理2的证明已完成。 定理4:CSP串通TPA伪造数据无法通过验证。 综上所述,文中方案能够有效地检测数据破坏或恶意伪造行为,从而确保数据审计方案能够安全实施。 该文实现了EMCA和文献[17,20]的原型系统,实验证明,EMCA大大减少了审计时间及计算开销。实验硬件环境为macOS操作系统,2.6 GHz六核Intel Core i7处理器,16 GB内存。 表3比较了EMCA与文献[17,20]在标签生成、证据生成和验证证据阶段的计算开销。为了简化表达式,使用Tmul,Texp,Tp,Thash和Tadd分别代表一次乘法运算、一次幂运算、一次双线性对运算、一次Hash运算和一次加法运算所需的时间。其中,n为数据块总数,r为副本数,e为批量审计的数据块数。对比得出,在标签生成和验证证据阶段,EMCA都是具有优势的,在整个审计过程中,与文献[17,20]相比,文中方案具有更低的计算开销。 表3 EMCA与文献[17,20]的计算成本比较 该文选择了0~200个数据块,5个副本,10个云存储服务器来比较EMCA与文献[17,20]在标签生成、证据生成和验证证据时的计算开销。 图2显示了标签生成的比较结果。当数据块数为200时,EMCA需要44 ms,而文献[17]需要1 010 ms,文献[20]需要2.5 s。很显然,文中方案的时间消耗要远小于文献[17,20]的时间消耗。 图2 标签生成的计算成本比较 图3显示了证据生成的比较结果。当审计数据块不断增多时,EMCA的计算成本比文献[17]的高,原因在于EMCA的计算成本集中在证据生成阶段,审计阶段所用开销极小;而文献[17]的计算开销集中在审计阶段,证据生成阶段开销较小。 图3 证据生成的计算成本比较 图4显示了验证证据阶段的比较结果。EMCA开销最小,当数据块数为100时,EMCA只需不到1 s,而文献[17]需要71 s,文献[20]需要8 s。很显然,在审计阶段,文中方案的计算成本远低于文献[17,20]的计算成本。原因在于EMCA验证阶段只需进行两次模幂和两次哈希,计算成本与审计数据块数无关,而文献[17,20]需要三次双线性对配对和多次哈希、幂运算、加法和乘法,且计算成本随审计数据块数增加而增加。 图4 验证证据的计算成本比较 图5显示了一次完整的审计过程的计算成本比较。从一次完整的审计过程来看,EMCA的计算开销远小于文献[17,20]的计算开销,如当审计数据块为100时,文献[17]一次审计需要71.8 s,文献[20]需要21 s,而EMCA只需1.3 s。原因在于EMCA舍弃了计算昂贵的双线性映射运算,采用了模幂加密技术来保证效率与安全。 图5 一次审计的计算成本比较 针对现有的多副本数据审计方案的不足,该文提出了一种在多云情景下的多副本数据完整性验证方案,副本数据可存储在不同的云存储服务器中,采用第三方审计者协助审计,通过同态可验证标签可一次批量审计所有抽样副本,大大提高了审计效率。实验分析与评估表明,该方案是安全和高效的。未来的工作是改进方案使用户不必参与审计过程,以减轻用户端负担。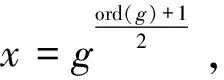
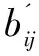
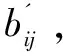
4 性能分析
4.1 理论分析

4.2 实验分析

5 结束语
