全向机器人在斜坡过渡中的稳定性研究
2024-03-24

林顯新1 苏茜1 叶城保1 李国进
摘 要:无人餐厅中全向机器人在架空轨道上从水平面运动到斜坡θ过程中,作用在麦克纳姆轮垂直方向的重力发生变化,破坏运动系统的稳定性,针对该运动过程系统稳定性差,稳定调整时间长等问题,提出采用遗传算法与PID控制相结合的方法对运动系统进行优化。本文构建全向机器人在斜坡过度中运动系统的数学模型,定值θ为扰动量,通过分析系统函数特征根在[s]复平面内的位置判定系统收敛性。采用改进遗传算法对PID控制器参数进行优化,研究系统稳定响应状态下的最优目标函数和最佳适应度变化趋势,获得Kp、Ti和Td参数。通过MATLAB/Simulink仿真结果表明,遗传算法与PID相结合的控制方法在迭代2次就获得最优控制目标函数,有效抑制了稳态误差,缩短稳定调整时间,提高了运输效率,对后续研究变值θ扰动的自动校正提供了一定参考价值。
关键词:全向机器人 遗传算法 PID 系统稳定性
1 引言
随着计算机控制技术与智能化的发展,服务类机器人得到快速发展,加上新冠疫情的影响,餐饮行业为了减少服务人员与消费者之间的接触,很多餐馆开始向“自主点菜+消费”的运营模式转型[1]。采用麦克纳姆轮的全向机器人在架空轨道上完成从厨房至饭桌的菜肴运输任务,其稳定性是决定无人餐厅运营效率的主要指标。本文通过分析机器人从平面过渡到斜坡上的运动状态,构建机器人在斜坡上运动的数学模型,优化其运动稳定性,提高菜肴运输效率。
2 构建运动系统模型
2.1 系统受力分析
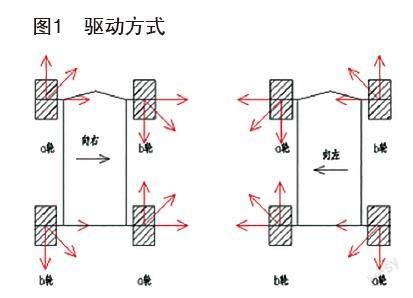
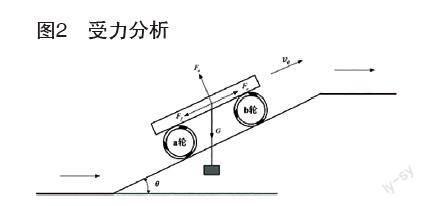
全向机器人在水平面运动,四轮在牵引力作用下克服摩擦力可实现加减速、匀速运动,系统稳定性较好[2-3]。当从水平进入斜坡过程,受斜坡角度θ变换作用,阻力变为重力分量和摩擦力之和,系统稳定性发生改变,全向机器人驱动模式和斜坡运动的受力分析图分别如图1和图2所示。
2.2 构建系统方框图
全向机器人采用STM32F103FD单片机作为控制核心,4路输出模块驱动4个步进电机带动ABAB型麦克纳姆轮实现向左、向右和前进、后退运动[4-5]。机器人下方连接托盘用于盛放菜肴,通过架空轨道实现菜品从厨房到餐桌的运输,其系统数学模型的方框图如图3所示。
系统前向通道环节包括驱动环节G1和执行环节G2,测量装置为同轴编码器。驱动系统在理想作用下,控制器作用于轮系输出的牵引力为fe1。
机器人与菜肴的质量约m,速度为v1。对式(1)作函数Laplace变换得出驱动环节的传递函数G1(s)。
全向机器人在角度为θ的斜坡上运动时,根据牛顿第二定律建立单级倒立摆系统,机器人在牵引力作用下克服摩擦力和重力分量运动,其方程式如下所示。
fe2为机器人在斜坡上的驱动力,轮子与轨道的摩擦力为fu=umgcosθ,斜坡上重力分量为fg=mgsinθ。
全向机器人在斜坡上的运动系统开环传递函数为HK(s)=NG1(s)G2(s),N表示系统干扰冲击非线性部分的描述函数,可作为一个变量的增益处理,即N>0。
运动系统闭环传递函数为HB(s)=HK(s)/1+
KHK(s),K为反馈环节。
全向机器人在斜坡上的运动系统是一个二阶系统,由式(6)的分母可以得到二阶系统的特征方程。
此方程的两个特征根为s1和s2。
当斜坡角度0<θ<90°,cosθ=[0,1],sinθ
=[0,1],m=13.5kg,K>0,若同比例反馈时,K取值为1,轮系与架空轨道之间的滚动阻力系数u=[0.010,0.018],本文取折中值u=0.015。因此有(um2gcosθ+m2gsinθ)>0,(um2gcosθ+m2gsinθ)2-4m2=(um2gcosθ+m2gsinθ+2m)(um2gcosθ+m2gsinθ-2m),而um2gcosθ+m2gsinθ+2m>0,(um2gcosθ
+m2gsinθ-2m)=m[mg(ucosθ+sinθ)-2],利用MATLAB数学实验,对[mg(ucosθ+sinθ)-2]取极值,仿真程序为:
1.x=0:pi/100:pi/2;
2.y=13.5*10*(0.015*cos(x)+sin(x))-2;
3.min(y);
4.max(y);
实验仿真结果有min(y)=0.025>0,
max(y)=133>0。因此有m[mg(ucosθ+sinθ)-2]
>0,(um2gcosθ+m2gsinθ)2-4m2>0,特征
根s1,2<0。
根据系统传递函数特征方程极点在[s]平面内的分布情况判定系统的稳定性,由于特征方程极点值s1,2<0,分布在[s]平面的左半部分,其特征根具有负实根或其负根有负实部,可以判定该二阶系统函数响应收敛稳定,当全向机器人在θ=30°的斜坡上运动,菜肴与机器人质量为1.35kg,摩擦系数u=0.015,N=700,K=500,则系统传递函数式(6)化简为
抽样控制点时长为1ms,假定系统在单位脉冲输入信号作用下,观察系统的响应输出,编写系统响应的MATLAB控制程序。
1.num=[382.5];
2.den=[1 5.13 273.2];
3.sys=tf(num,den);
4.t=0:0.02:10;
5.h=impulse(num,den,t);
6.figure(1),plot(t,h);
7.xlabel('Time/s');ylabel('State response');
系统响应的实验仿真结果如下图4所示。
从系统响应状态波形图可以得出,系统在经历多次振荡后,并在t=3s后趋于稳定,为减少振荡对系统的冲击影响,缩短稳定时间,需对系统结构进行优化。
3 系统稳定性优化
3.1 串联PID控制器
由于被控对象的复杂性和干扰的不确定性,传统的PID控制方式在参数整定方面具有较大的局限性[6-7],仅依靠技术人员的工程经验随机拼凑参数进行校正,选值时间长、误差大,影响系统校正效果。
在已知系统函数稳定收敛的前提下,为优化系统的响应性能,消除偏差提高响应的快速性和准确性[8],本文采用智能算法中的遗传算法设计PID控制器,将采样数据和参考值进行比较获得差值,通过对这个差值迭代、遗传控制获得PID校正参数。再把这个差值用于PID控制器重新计算新的输入值对系统进行校正,使系统的目标值保持或者达到参考值范围。串联PID控制器的系统数学模型如图5所示。
PID控制器作为线性控制器,根据斜坡角度θ的改变,全向机器人从水平面进入斜坡的速度将根据斜度θ变化而发生变化,单片机输出给系统的给定速度值Vd(t)与系统实际输出的速度值Vo(t)构成控制偏差为ε(t)。
根据PID控制原理,对偏差进行校正获得新的速度值V(t)。对控制偏差进行比例、积分和微分变换的PID控制规律为
式中,Kpε(t)为比例控制项,Kp为PID控制的比例系数;为积分控制项,Ti为积分时间常数;为微分控制项,Td为微分时间常数,将PID控制规律转化成传递函数的形式
通过式(10)可知,全向机器人在斜坡的运动系统是一个二阶系统,根据二阶系统的特性,结合系统特定的性能指标,采用遗传智能算法整定PID参数Kp、Ti和Td。
3.2 遗传算法整定PID参数
遗传算法借鉴于生物界自然选择和自然遗传学机理上的迭代自适应概率性搜索,模仿生物进化步骤,通过引入了选择、交叉和变异算子,进而获得最优种群[9-10]。
3.2.1 搭建遗传算法的框架
本文设计了遗传算法整定PID的Kp、Ti和Td参数,通过构造适应度函数、交叉算子、变异算子和约束条件,从上一代种群中将适应度较高的个体选择出来,用以优化种群,从优化出来的种群中随机抽取一对个体,进行多位交叉,生成新群体,达到增大搜索空间的目的,防止选择和交叉丢失而设置约束条件的变异函数,以强化搜索效率和搜索能力,提高收敛能力。
3.2.2 设计遗传算法的步骤
(1)确定决策变量和约束条件
PID控制的三个参数为Kp、Ti和Td,根据参数的物理意义和经验来确定它们的取值范围,即设置约束条件Kp的参数取值范围为[0,10],Ti的参数范围为[0,1],Td的参数范围为[0,1]。
(2)构建最优目标函数
为获取全向机器人从水平进入斜坡过渡过程的理想动态特性,采用速度偏差绝对值时间积分性能指标作为参数选择的最小目标函数[11-12]。为防止寻优种群控制量过大,在目标函数中加入控制输入的平方项,用以划定控制量的。最后选用以下公式作为参数选择的最优目标。
根据式(12)PID的控制规律,为更好的对系统输出进行校正,ε(t)作为系统实际输出与目标输出的偏差,是系统校正对象,V(t)为ε(t)经过PID控制器校正以后的新输出速度值(系统校正后的输入),tv为系统稳态上升时间,w1,w2,w3为寻优目标函数的加权值。同时,为抑制超调,获得一个稳态响应,采用遗传算法的处罚功能,设置超调限值,如系统超调量一旦超越限值,将增加加权项w4抑制超调,通过分析系统实际输出的误差作为最优目标函数的一项,即如果误差e(t)<0,此时最优指标变为:
(15)
其中,w4为加权值,且w4>w1,e(t)=Vo(t)-Vo(t-1),Vo(t)为系统被控对象的实际输出。
(3)确定编码和解码方法
以实数编码的方式将Kp、Ti和Td参数以0.01等分进行随机排序作为个体的初始基因进行遗传进化。其中,取各自区域中间值N作为遗传比较基因,大于N的基因被解码优化编为0进行遗传进化,将编号为0的基因个体作为淘汰线重新解码,把遗传迭代2次再作为一个新种群进行优化。例如,以Ti的参数[0,2]为例按0.01等分划分200份个体,随机抽K=10个个体进行编码解码,设N=1.10,迭代1次,N=1.14作为遗传迭代2次,如下图所示。
(4)确定个体评价方法
本文将最少迭代次数的路径值作为适应度函数(个体评价方法)的一个重要指标,为了实现种群在进化过程中获得最优基因,通过自适应交叉概率函数将迭代遗传后的种子个体相互交叉,调节种群个体交叉概率,尽可能增加寻优种群的多样性,扩大寻优范围。针对基因选择过程,本文采用轮盘赌策略进行选择操作,以减小偏差,Kp的值取区域值的上半区;以消除静态误差,提高系统的无差度为目的,积分强度越强,Ti的值取区域值下半区;从偏差信号的变化率,加快系统的反应速度,减少调节时间,取Td的值取区域值上半区。
(5)确定遗传算法的运行参数
根据Kp、Ti、Td值的约束条件,结合全向机器人在斜坡运动系统的实际情况确定群体大小Size=60、遗传代数G=100、交叉概率Pc=0.9、变异概率Pm不固定,加权值w1=0.999,w2=0.001,w3=2,w4=100。
4 实验仿真结果与分析
4.1 实验结果
全向机器人从水平面过度到斜坡的运动过程中,作为倒立摆系统,被控量为机器人移动速度,输入是θ为定值(固定斜坡)的单位脉冲信号,设置系统响应输出的抽样间隔时间为1ms。针对系统传递函数式(10)编写遗传算法的PID控制器程序代码,通过MATLAB/Simulink仿真并運行,获得遗传算法优化过程(迭代次数)和最佳适应度值变化趋势(系统响应曲线)如图6和图7所示。
4.2 实验结果分析
通过仿真实验,从图6目标函数优化过程中可知,在遗传次数超过2代以后,最优目标函数为BestJ=61.1679,图7为整定后的PID控制在阶跃响应,响应曲线经过一次振荡后,在t=0.1s后趋于稳定,返回PID参数为Kp=3.3398、Ti=0.1123和Td=0.1670。对比传统PID控制器校正方式,改进遗传算法+PID算法相结合,改良了系统的动态性能,缩短了参数整定时间,提高了参数整定精度,对系统的动态性能有很好促进作用。
5 结论
本文以提高无人餐厅架空轨道机器人运输菜肴的效率为目的,进一步优化全向机器人在斜坡上运动的稳定性,提出了一种基于遗传算法与PID相结合的控制算法。利用倒立摆系统牛顿第二定律和拉普拉斯变换建立了系统在斜坡上运动的数学模型,通过判定传递函数特征根在[s]复平面的左半部分,并分析系统的动态响应新能指标。针对系统响应性能,根据定值θ干扰冲击特征使系统适应度函数依据控制系统的指标函数而设定,用实数编码方式将约束条件的区域值随机编码、解码,再对较优种群重新随机编码,加大交叉概率,增加基因多样性,扩大寻优范围,最终通过迭代2次,获得最佳目标函数值,有效抑制系统稳态误差。仿真实验结果表明,通过遗传算法与PID相结合的控制算法对采用全向机器人在斜坡上运动的稳定性优化有效可行,缩短了稳定调节时间,减少了系统超调,对后续研究变值θ扰动的自动校正提供了一定参考价值。
基金项目:2023年度广西高校中青年教师科研基础能力提升项目(2023KY1115)“基于全向機器人在斜坡过渡中的稳定性研究”,项目主持人:林显新。
参考文献:
[1]牛国君,曲翠翠,潘博,付宜利.含有广义饱和函数的全局渐近稳定非线性PID控制[J].机器人,2020,42(05):568-582.
[2]林显新.基于PID控制的全向移动机器人运动连接系统仿真研究[J].食品与机械,2021,37(03):102-104+111.
[3]张品,李长勇.基于改进模糊PID的全向搬运机器人路径跟踪控制研究[J].食品与机械,2021,37(06):114-119+190.
[4]刘伟,马彪,马利强,陈雪辉,俞传阳,黄磊,李昊.卡尔曼滤波融合遗传PID控制算法在提高播种精度中的应用[J].安徽农业大学学报,2021,48(04):674-679.
[5]袁梦飞,阚秀,曹乐,王夏霖,吴健珍,罗晓.自适应精英遗传算法的快递车路径规划[J].导航定位学报,2021,9(06):104-111.
[6]吕志忠,汪维杰,陈金鹏,姚茂江,林清宽,张成维.四足磁吸附爬壁机器人稳定性与动力学分析[J].哈尔滨工程大学学报,2022,43(03):429-435.
[7] Rosy Pradhan,Santosh Kumar Majhi,Jatin Kumar Pradhan,Bibhuti Bhusan Pati.Optimal fractional order PID controller design using Ant Lion Optimizer[J].Ain Shams Engineering Journal,2019,(10),Pages:281-291.
[8] Qian Shi,Hak-Keung Lam,Chengbin Xuan,Ming Chen..Adaptive neuro-fuzzy PID controller based on twin delayed deep deterministic policy gradient algorithm[J].Neurocomputing, 2020,(03),Pages:183-194.
[9]韩宝玲,汪清强,贾燕,罗庆生,朱琛.提升四足机器人行走稳定性的对角步态规划方法[J].北京理工大学学报,2018,38(09):917-920+926.
[10]李方能,陈鑫,江山,江鹏飞.高精度陀螺稳定平台控制系统参数整定方法[J].海军工程大学学报,2021,33(05):7-12.
[11]陈灿辉,黄春庆.PID控制器中随机干扰控制方法的设计与实现[J].计算机仿真,2021,38(09):227-230.
[12]徐凯,林显新,易丐,李国进.基于架空轨道的全向移动机器人运动稳定性研究[J].食品与机械,2020,36(02):105-109.
[13]苗智英,李瑞琴,张启升,梁晶晶,孟宏伟,梁世杰.3-PUU轮腿式移动机器人的步态与稳定性分析[J].机械传动,2018,42(03):90-93.
