Optimal Shape Factor and Fictitious Radius in the MQ-RBF:Solving Ill-Posed Laplacian Problems

Chein-Shan Liu ,Chung-Lun Kuo and Chih-Wen Chang

1Center of Excellence for Ocean Engineering,National Taiwan Ocean University,Keelung,202301,Taiwan

2Department of Mechanical Engineering,National United University,Miaoli,36063,Taiwan

ABSTRACT To solve the Laplacian problems,we adopt a meshless method with the multiquadric radial basis function(MQRBF)as a basis whose center is distributed inside a circle with a fictitious radius.A maximal projection technique is developed to identify the optimal shape factor and fictitious radius by minimizing a merit function.A sample function is interpolated by the MQ-RBF to provide a trial coefficient vector to compute the merit function.We can quickly determine the optimal values of the parameters within a preferred rage using the golden section search algorithm.The novel method provides the optimal values of parameters and,hence,an optimal MQ-RBF;the performance of the method is validated in numerical examples.Moreover,nonharmonic problems are transformed to the Poisson equation endowed with a homogeneous boundary condition;this can overcome the problem of these problems being ill-posed.The optimal MQ-RBF is extremely accurate.We further propose a novel optimal polynomial method to solve the nonharmonic problems,which achieves high precision up to an order of 10-11.

KEYWORDS Laplace equation;nonharmonic boundary value problem;Ill-posed problem;maximal projection;optimal shape factor and fictitious radius;optimal MQ-RBF;optimal polynomial method

1 Introduction

A multiquadric(MQ)radial basis function(RBF)

was used by Franke [1] to interpolate the given scattered data in a bounded domain Ω.Here,rj=is the distance between(x,y)and(xjc,yjc).

The solution for a two-dimensional (2D) problem may be expanded as a linear combination ofφj,such asu=.The expansion coefficientsajare then determined by the governing equation and boundary conditions.One advantage of the MQ-RBF is that its bases in Eq.(1)involve only the single parameterjfor both 2D and three-dimensional(3D)problems.These problems havenunknown coefficientsaj.The Pascal polynomial bases have two parameters(i,j)inxiyi-jfor the 2D problem,and three parameters(i,j,k)inxiyi-jzj-kfor 3D problems.Therefore,for the Pascal polynomial bases,the number of unknown coefficientsaijisn(n+1)/2 for the 2D problem and the number of unknown coefficientsaijkisn(n+1)(n+2)/6 for the 3D problem.

Kansa[2]first adopted the MQ-RBF to solve partial differential equations(PDEs).However,asnincreases,the MQ-RBF becomes increasingly ill-conditioned;hence,Liu et al.[3]proposed a multiplescale MQ-RBF method to mitigate this ill-conditioning to solve elliptic-type PDEs.The accuracy of the MQ-RBF heavily depends on the shape factor and the number of center points (for which no theoretical optimal value is known);hence,determining the optimal values of parameters is critical[4–7].When Iurlaro et al.[8] applied an energy based method,Noorizadegan et al.[9] adopted the effective condition number technique to determine the optimal shape factor.Although the original RBF centers in the Kansa method[2]were distributed inside the domain and boundary,researchers later developed the fictitious point method to improve the performance of the MQ-RBF by locating the centers inside a curve enclosing the domain[9,10].They found that the accuracy is greatly improved if the centers are distributed sufficiently far outside of the problem domain.

The seeking of an optimal value of the shape factor is a tricky problem for determining RBFs for the interpolation of PDE problems [11–15].In accordance with the linear algebraic theory,Liu [16]asserted that the nonharmonic boundary value problem for the Laplace equation is ill-posed because in the resulting linear systemAx=b,bdoes not lie in the range space ofA;hence,no coefficient vectorxexists for the expansion of the solution.Liu[16]enlarged the range space ofAand improved the accuracy using hybrid method.

Inφj,the center points(xjc,yjc)and the shape factorcmust be determined;however,simultaneously determining the optimal values of these parameters is difficult.In[17],the optimal shape factor was determined by minimizing the energy gap functional.Many numerical solutions for engineering problems have been obtained through polynomial methods[18–22].Recently,Oruc[23]developed a local mesh-free radial point interpolation method for solving the Berger equation for thin plates.We intend to improve the polynomial method for solving the nonharmonic boundary value problems of Laplace equation.Briefly,the innovations of this paper are as follows:

• A novel method was developed to determine both the optimal values of the fictitious radius and shape factor in the MQ-RBF for solving the Laplace equation.

• A new merit function was derived to determine the optimal values of parameters.

• The relationship between the maximal projection and the effective condition number was derived for the first time.

• A highly original idea was used the sample function to compute the merit function.

• The nonharmonic problem was transformed to the Poisson equation with homogeneous boundary conditions.

• An optimal polynomial method was developed to solve the nonharmonic problems.

• Highly accurate solutions for the nonharmonic problems were obtained.

The remaining parts of the paper proceed as follows.In Section 2,we introduce the maximal projection technique.In Section 3,we derive the MQ-RBF and demonstrate that the optimal values of the shape factor and fictitious radius are obtained when a merit function derived from the maximal projection technique is minimized;the section also introduces a novel sample function for calculating the merit function.In Section 4,we present numerical examples of the Dirichlet,mixed,and Cauchy problems of the Laplace equation.In Section 5,we introduce the nonharmonic problem and transform it to the Poisson equation endowed with a homogeneous boundary condition;the section also provides numerical examples that illustrate how solutions are obtained with the optimal MQ-RBF and optimal polynomial method.Finally,in Section 6,we conclude the paper.

2 Maximal Projection

In many applications,an unknown vectorx∈Rnthat is the output of a linear model must be found.This can be achieved by solving a linear system:

whereA∈Rn×nis the given nonsingular coefficient matrix of the linear model,andbis a given input vector.

We attempt to find the best approximation tobfromxby finding the optimal value of the shape factorcin the MQ-RBF,which related toA.The error vector is

where we lety=Axfor notational simplicity.By minimizing

or maximizing

the optimal approximation ofxcan be found;this is named the maximal projection solution.

Becausebis a given nonzero constant vector,we can recast Eq.(5)as

which does not affect the solution ofx.We then minimize the following merit function:

which is the reciprocal of Eq.(6).

By applying Eq.(7),Liu [24] developed efficient methods to solve Eq.(2) iteratively.Liu [24]employed a scaling invariant property of Eq.(7) (i.e.,yandβy,leading to the same value offifβ0) to derive a maximal projection solution in an affine Krylov subspace and proved that Eq.(7)implies the least-squares solution.

3 Optimal Shape and Fictitious Radius

Consider

whereΓ:={r=ρ(θ),0≤θ≤2π} is the boundary of a bounded domain Ω,andρ(θ) is a radius function ofΓthat encloses Ω.

In the MQ-RBF method,the trial solutionu(x,y)of Eqs.(8)and(9)is given by

By considering Eqs.(10),(8),and(9)atnq=m1×(m2-1)+nbcollocation points,we obtain

wherea:=(a1,...,an)T,and the componentsGijofGandbjofbare given in the Appendix.The first part generates linear equations from the governing equation,whereas the second part generates linear equations from the boundary condition.The dimension ofGisnq×n,and Eq.(11)withn=nqcan be used to finda.In general,we first selectm10andm20;then,n=m10×m20.Next,nb=n-m1×(m2-1)can be computed,wherem10×m20>m1×(m2-1).

To make Eq.(11)less ill-posed,we suggest the multiple-scale MQ-RBF in[3]

as a trial solution.The multiple-scale coefficientsskare determined by

wheres1=1 andGkdenotes thekth column ofG.

Upon letting

we obtain a newn-dimensional square linear system:

Din Eq.(14)acts as a postconditioner to ensure thatAis better conditioned than isG.Whennis not sufficiently large,we can employ the Gaussian elimination method to calculate the expansion coefficients ina.

To determine the optimal value of shape factorc,let

Inserting Eq.(16)andbinto Eq.(7),we can minimize

in a given interval [a,b] by the one-dimensional golden section search algorithm (1D GSSA) with a loose convergence criterion ofε1=10-2.When the optimal shape factor has been obtained,the numerical solution in Eq.(12)can be obtained by inserting the shape factor into Eq.(15)and solving fora.

In Eq.(17),the exactais not yet known.As is the case in[7],we suppose a sample solutionus(x,y) that satisfies the Laplace equation but not the boundary conditions.Many polynomial functions automatically satisfy the Laplace equation,such as the two simple sample functions ofus(x,y)=x+yandus(x,y)=xy,which are,respectively,the first-order and second-order solutions of Laplace equation.We then interpolateus(x,y)with the basesφjatncollocated points:

Becauseus(x,y)is a simple function,we can computefrom the linear system(18)rapidly;this is then inserted into Eq.(17)to computef:

Ais still computed with Eq.(14),which hascas one of its parameters.Liu et al.[17]determined the optimal shape factor by using the energy gap functional;however,this method is more complicated than the method of using the merit functionfhere.

To determineDandcsimultaneously,we can consider the minimization

which can be performed by the 2D golden section search algorithm(GSSA)with a loose value ofε2=10-2.The 1D GSSA in Tsai et al.[26]is much simpler than the 2D case.In general,for high-dimensional search algorithms,the obtained minimum is normally a local minimum and not the global minimum.Ais still computed by Eq.(14),involvingcandDas parameters.Solving Eq.(20),we can determine the optimal values ofcandD.This method is called the optimal MQ-RBF.The GSSA was used by Tsai et al.[26]to find a good shape factor.

Remark 1.Recently,Noorizadegan et al.[9]demonstrated that the effective condition number can provide a much better estimation of the actual condition number of the resultant matrix-vector system(15),and they proposed applying the effective condition number as a numerical tool to determine a reasonably good shape factor in the MQ-RBF.Eq.(15)in[9]is

whereκis the traditional condition number,κeff=‖b‖/(σn‖a‖) is the effective condition number,andσ1andσnare,respectively,the largest and smallest singular values ofA.

Let us estimate the maximal projection(MP)in Eq.(6)denoted as

We chooseAa=σ1ain the numerator andAa=σnain the denominator;we can thus obtain the largest value ofF.We then have

whereα2=(a·b)2is some positive constant.Definingκ=σ1/σn,

In combination with Eq.(21),we can derive

Therefore,the minimization in Eq.(17)is equivalent to the maximization of the effective condition number.Noorizadegan et al.[9]found that the shape factorccorresponding to the maximum effective condition number resulted in the numerical solution with the smallest error.This observation is consistent with the presented formulation resulting from this MP-based technique.

We have thus demonstrated that the shape factor obtained with our MP technique and the previous effective condition number technique are equally effective.However,our strategy of selecting the optimal shape factor is much simpler.The computational cost of finding the optimal (c,D) is low becausein Eq.(20)is computed from the data interpolation(18)by a given sample functionus(x,y).

4 Numerical Examples

We assess the errors ofu(x,y),(x,y)∈in terms of the maximum error(ME)and root-meansquare-error(RMSE)as follows:

whereueanduNdenote the exact and numerical solutions,respectively.Fig.1 presents plots of the ME with respect toθ,which are obtained as follows:

we selectedNt=n1×n2=100×20=2000.

4.1 Example 1

We consider the following two exact solutions of the Laplace equation:

Figure 1:MEs of the solutions for the sample function us=xy with(a)u(x,y)=x2-y2 and(b)u(x,y)=cosx sinhy+sinx coshy

The corresponding boundary shapes are,respectively,

This example is simple;however,we use it to demonstrate the performance of the proposed method.For Eqs.(29)and(31),we take n=512,nb=112 and D=7 to obtainc.We test two sample functions,us=x+yandus=xy.In the interval[a,b]=[1,1.5]withus=x+y,the optimal valuec=1.309 is obtained after ten iterations in the GSSA forε1=10-2.The ME and RMSE of the numerical solution compared withu(x,y)=x2-y2in the entire domain are 5.14×10-8and 2.28× 10-9,respectively.Moreover,computing the optimal value ofcrequired only 5.35 s of CPU time;the condition number was 5.7×107.

Similarly,forus=xyand [a,b]=[1,3],the optimal valuec=2.235 was obtained within 13 iterations,and ME=9.59×10-9and RMSE=3.87×10-10were obtained.Fig.1a presents a plot of the ME at each angleθ∈[0,2π].For this solution,the CPU time was 5.31 s,and the condition number was 8.75×106.Hence,highly accurate solutions can be generated from bothus=x+yandus=xy,despite the substantial difference betweenc=1.309 andc=2.235.Moreover,neither condition number is too large.Unless otherwise specified,we employus=xyas the sample function in the following computations.

For a fixed interval of[a,b],we,in general,can obtain a local minimum in that interval by using the GSSA.To obtain the global minimum,we can search in various intervals and compare the minimums of each sub-interval to identify the global minimum.However,this technique is time-consuming.For a large interval[a,b]=[1,5],the results forc,ME,RMSE and the condition number(CN)are listed in Table 1.The result obtained with a large interval [a,b]=[1,5] (c=3.505) is more accurate than that obtained by picking the smallest of the local minimums at four subintervals (c=3.764).This suggests that the MQ-RBF is sensitive to the value of the shape factorc.Therefore,we selected a suitable interval by performing some trials;the interval must be sufficiently large.

Table 1:Comparison of c,ME,RMSE,and CN for different intervals[a,b]

This example allows us to discuss the role ofDin Eq.(14).If we takeD=I nin Eq.(14),the linear system(15)is not regularized by the multiple-scale coefficients.ForD=In,the ME=6.19×10-8and RMSE=2.72×10-9are larger than the ME=9.59×10-9and RMSE=3.87×10-10obtained by the regularization method.

For Eqs.(30) and (32),changing the values ton=450,nb=210,D=7,and [a,b]=[1,2],we obtained a proper valuec=1.416 with 11 iterations in the GSSA.Ifu(x,y)=cosxsinhy+sinxcoshy,the ME was 2.09×10-11and the RMSE was 1.9×10-12.Fig.1b presents a plot of the ME for each angleθ∈[0,2π].The CPU time was 3.31 s,and the CN was 2.48×107.

Table 2 presents the accuracy for variousDvalues with the other parameters held constant.

Table 2:Optimal value of c and accuracy for various values of D

Table 2 reveals thatDaffectsc,the ME,and the RMSE.Hence,to enhance the accuracy,we can apply Eq.(20)to select the optimal values of bothcandD.

For n=512 andnb=112 in the range[a1,b1]×[a2,b2]=[1,3]×[6,8],the optimal values ofc=2.52 andD=7.176 were obtained with 13 iterations of the GSSA forε2=10-2.Compared withu(x,y)=x2-y2,ME=6.51×10-9and RMSE=2.59×10-10;hence,the accuracy is higher than if onlycwas optimized.Because both the optimal values ofcandDwere computed,the CPU time increased to 18.15 s.The CN was 4.8×107.If the range is enlarged to[a1,b1]×[a2,b2]=[1,5]×[1,10],we obtainc=4.086 andD=6.52;however,ME=7.55×10-9and RMSE=4.04×10-10,which are slightly larger than those for the smaller range.For the larger range,the CPU time increased to 21.91 s,and the CN decreased to 3.91×107.

For the sample functionus(x,y)=excosyin the range[a1,b1]×[a2,b2]=[1,2]×[6,8],the optimal values ofc=1.212 andD=6.996 were obtained with 10 iterations in GSSA forε2=10-2.Compared withu(x,y)=cosxsinhy+sinxcoshy,ME=1.92×10-11and RMSE=1.84×10-12;this was again more accurate than when onlycwas optimized.The CPU time was 9.76 s,and the CN was 1.15×107.

4.2 Example 2

We consider the mixed BVP with two solutions given by Eqs.(29)and(30):

where Γ1:={r=ρ(θ),0≤θ≤π},Γ2:={r=ρ(θ),π <θ <2π},andun(ρ,θ)is the normal derivative ofuon the boundary Γ2.The boundary shapes are still given by Eqs.(31)and(32).

For the first mixed BVP,we fixn=512 andnb=112 and seek the proper values ofcandDin the range[a1,b1]×[a2,b2]=[1.5,1.9]×[8.1,9.5].The optimal valuesc=1.847 andD=9.445 were obtained after 12 iterations,and ME=7.21×10-9and RMSE=4.06×10-10relative tou(x,y)=x2-y2.The CPU time was 20.47 s,and the CN was 3.56×107.

For the second mixed BVP,we fixn=450 andnb=210,and in[a1,b1]×[a2,b2]=[1,1.5]×[7,8],we obtain the optimal valuesc=1.335 andD=7.705 with 11 iterations in GSSA underε2=10-2.ME=5.33×10-11,and RMSE=3.13×10-12.The CPU time was 13.29 s,and the CN was 2.31×108.

4.3 Example 3

A Cauchy inverse boundary value problem with two solutions given by Eqs.(29)and(30)can be formulated as follows:

whereg(x,y)is an unknown function to be recovered.We add noise as follows:

whereRindicates random numbers with zero mean.

For the first Cauchy problem we fixn=250,nb=170 ands=0.1,and seek the proper values ofcandDin the range[a1,b1]×[a2,b2]=[0.5,1]×[6,8].The optimal valuesc=0.803 andD=6.468 were obtained with 13 iterations in GSSA underε2=10-2.ME=1.65×10-2and RMSE=6.7×10-3were obtained with reference tou(x,y)=x2-y2on Γ2.In Fig.2a,we present a comparison of the numerical and exact values forgin the rangeθ∈[π,2π].

Figure 2:Comparison of the numerical and exact solutions on the lower half boundary for the Laplace equation with Cauchy boundary conditions on the upper half boundary.Solutions for(a)Eqs.(29)and(b)(30)

The optimal valuesc=0.856 andD=7.743 were obtained for the second Cauchy problem.ME=1.99×10-2and RMSE=8.14×10-3were obtained,and the numerical and exact values ofgin the rangeθ∈[π,2π] are compared in Fig.2b.For the ill-posed Cauchy problem,the optimal MQ-RBF is highly accurate even in the presence of substantial noise.

Remark 2.Because the distance function is used in the MQ-RBF,the proposed method is easily extended to 3D problems by takingrj:=.However,this may be accompanied by a considerable increase in CPU time.MQ-RBF is known to have a conditionally positive definite kernel;hence,the invertibility of the resulting interpolation matrix is not guaranteed unless the MQ interpolation is augmented with a polynomial basis.In a future study,we may extend the proposed method to Gaussians or inverse MQ-RBFs and to 3D problems.

5 Nonharmonic Boundary Value Problems

In this section we examine the nonharmonic problem of Eqs.(8)and(9),where

The nonharmonic problem comprises Eqs.(8),(9)and(31),whereh(x,y)=x2y3is a benchmark problem.Liu [16] developed a hybrid method denoted MMM for this benchmark problem and obtained a favorable result.

Let

be a new variable;we can then obtain the Poisson equation with a homogeneous boundary condition:

wherep(x,y)=Δh(x,y)=6x2y+2y30,becauseh(x,y)is a nonharmonic function.Whenv(x,y)has been solved,we can findu(x,y)=h(x,y)-v(x,y).

We first apply the optimal MQ-RBF to solve this nonharmonic problem;the results are presented in Fig.3.We fixn=525 andnb=445 and seek the proper values ofcandDin the range[a1,b1]×[a2,b2]=[0.9,1.8] × [3,6].The optimal valuesc=0.901 andD=3.004 were obtained with 13 iterations in GSSA withε2=10-2.Remarkably,ME=1.77×10-8and RMSE=5.35×10-9compared withh(x,y)=x2y3on Γ.Fig.3a presents a comparison of the numerical and exact solutions in the rangeθ∈[0,2π];the errors are plotted in Fig.3b.We placed many more points on the boundary than that in the interior;this can enhance the accuracy.

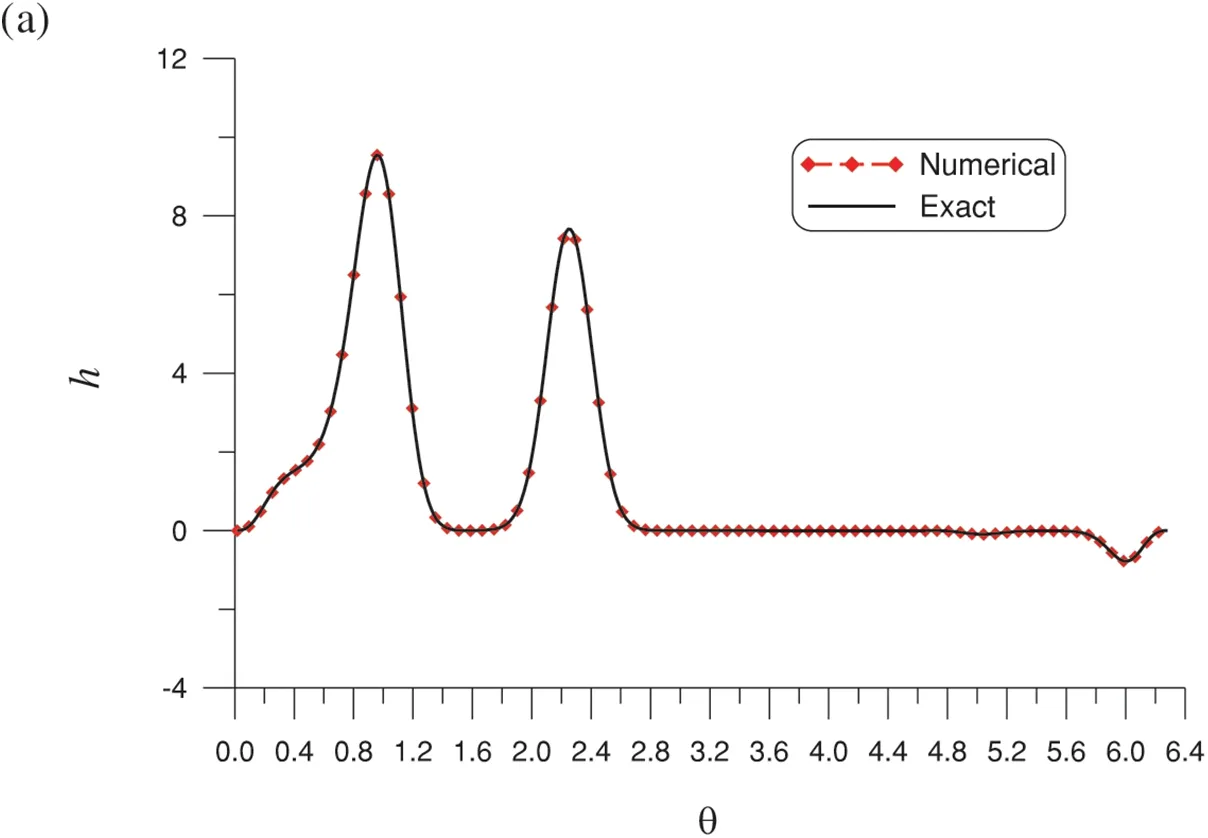
Figure 3:(Continued)

Table 3 presents a comparison of the MEs of the proposed method and methods in previous studies [13,16].The optimal MQ-RBF outperforms other methods in terms of accuracy by four to six orders of magnitude.

Table 3:Comparison of the ME for the benchmark problem for the proposed method and methods in the literature

To obtain a more accurate solution forv(x,y)and henceu(x,y)=h(x,y)-v(x,y),we consider the multiple-scale Pascal triangle polynomial expansion method developed by Liu et al.[18]:

After collocatingnqpoints to satisfy the governing equation and boundary condition(40),we have a non-square linear system(15)for which the scalessijare determined such that each column of the coefficient matrixAhas the same norm.Similarly,we can employ the following minimization:

to determine the optimal value ofR0.We apply the GSSA to solve this minimization problem with a convergence criterionε1=10-4.

Using the optimal polynomial method(OPM),we first test a direct problem in Eqs.(30)and(31).We takem=15,nq=130×5=650,and[a,b]=[1,5].The optimal valueR0=1.000024 was obtained after 24 iterations.For 2000 inner test points,ME=2.56×10-7and RMSE=1.62×10-8.

For the nonharmonic boundary value problem,we fixh(x,y)=x2y3and consider the domains with the following shapes:

For the five-star shape,we use the new OPM withm=10,nq=100×4=400 and [a,b]=[500,1500].After 34 iterations,the optimalR0=1450.829 was obtained.The results are presented in Fig.4a,and the corresponding errors are plotted in Fig.4b.For 400 test points on the boundary,ME=5.85×10-11and RMSE=2.68×10-11are countered.

To apply the new OPM for the nonharmonic problem with a peanut shape,we takem=6,nq=100×4=400,and[a,b]=[10,1500].After 34 iterations,the optimalR0=1365.607 was obtained.The results are presented in Fig.5a,and the corresponding errors are plotted in Fig.5b;ME=3.83×10-13,and RMSE=1.34×10-13.

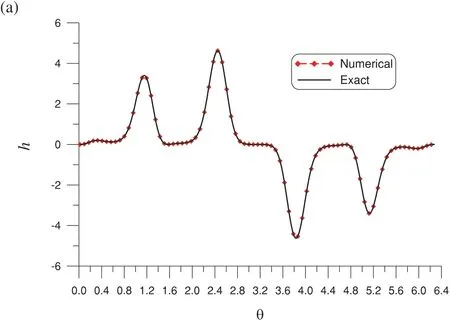
Figure 4:(Continued)

To apply the OPM for the nonharmonic problem with an amoeba shape,we takem=10,nq=100×4=400,and[a,b]=[1000,1500].After 30 iterations,the optimalR0=1398.8204 was obtained.The results are presented in Fig.6a,and the corresponding errors are plotted in Fig.6b;ME=2.39×10-11,and RMSE=9.76×10-12.The accuracy is three orders of magnitude better than that from the optimal MQ-RBF(Fig.3).

Figure 5:(Continued)

For a benchmark problem,the OPM achieves an accuracy of the 11th order;this is far superior to results in the literature with 3rd-order accuracy [13].The instances of [a,b] of [1,5],[500,1000],[10,1500],and[1000,1500]used for the different problems were configured to be sufficiently large to ensure that the solutions had high accuracy;this was achieved through trial and error.

Finally,we compared the performance of the OPM and the optimal MQ-RBF for a nonpolynomial nonharmonic functionh(x,y)=sinxcosyon a peanut shape.

Figure 6:(Continued)

For the OPM,we takem=15,nq=100×4=400,and [a,b]=[1000,1500].After 32 iterations,the optimalR0=1072.076 was obtained.The results are presented in Fig.7a,and the corresponding errors are plotted in Fig.7b;ME=5.86×10-12and RMSE=2.5×10-12.

For the optimal MQ-RBF,we fixn=525 andnb=445 and seek the proper values ofcandDin the range [a1,b1]×[a2,b2]=[0.9,1.8] ×[3,6].The optimal valuesc=1.341 andD=5.006 were obtained after 13 iterations.In this case,the optimal MQ-RBF result is competitive with that of the OPM(Fig.7);the method achieved ME=8.98×10-12and RMSE=3.09×10-12relative toh(x,y)=sinxcosyon Γ.

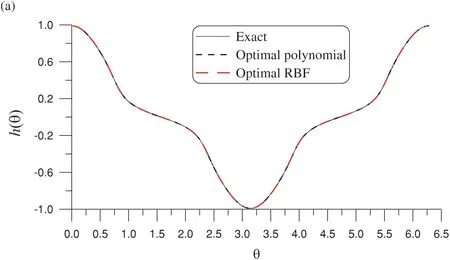
Figure 7:(Continued)

6 Conclusions

The key achievements of the paper are summarized as follows:

• By using the MP technique between two vectors,which is equivalent to the minimization in Eq.(5),merit functions were derived for determining the optimal values of the shape factor and fictitious radius in the MQ-RBF.

• The similarity between the MP and the effective CN techniques was demonstrated.

• Searching for a minimum in a preferred range was easily performed by using the sample function.Moreover,only a few operations in the GSSAs were required to determine the optimal shape factor and fictitious radius of the source points.The novel idea of inserting a sample function into the merit function is crucial in this technique.

• The optimal MQ-RBF is equally stable and accurate regardless of whether it is used to solve the Dirichlet,mixed,or Cauchy problems from the Laplace equation.

• With different boundary values,the optimal MQ-RBF offered different optimal shape factor and optimal fictitious radius parameters at different ranges.

• The algorithm is more accurate when the regularization diagonal matrixDis used.

• The optimal MQ-RBF method is much more accurate for solving the benchmark problem than those reported in the literature.

• A novel OPM was also developed to solve nonharmonic problems with high accuracy.

Acknowledgement:Thank all the authors for their contributions to the paper.

Funding Statement:This work was financially supported by the the National Science and Technology Council(Grant Number:NSTC 112-2221-E239-022).

Author Contributions:The authors confirm contribution to the paper as follows:study conception and design:Chein-Shan Liu,Chung-Lun Kuo,Chih-Wen Chang;data collection:Chein-Shan Liu,Chih-Wen Chang;analysis and interpretation of results: Chein-Shan Liu,Chih-Wen Chang,Chung-Lun Kuo;manuscript writing:Chein-Shan Liu,Chih-Wen Chang;manuscript review and editing:Chein-Shan Liu,Chih-Wen Chang.All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials:Data will be made available on request.

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.

Appendix

In this appendix,we lay out the code in the computer program used to obtain:

k=0

Do i=1,m10

θi=2πi/m10

Do j=1,m20

k=k+1

and the componentsGijandbjofGandbin Eq.(11):

Do i=1,m1

θ=2πi/m1

Do j=1,m2-1

xj=jρ(θ)/m2cosθ,yj=jρ(θ)/m2sinθ

K=m2(i-1)+j

bK=0

Do L=1,n

Do i=1,nb

θ=2πi/nb

xj=ρ(θ)cosθ,yj=ρ(θ)sinθ

bK=h(xj,yj)

Do L=1,n

K=m1×(m2-1)+i