THE RIEMANN PROBLEM FOR ISENTROPIC COMPRESSIBLE EULER EQUATIONS WITH DISCONTINUOUS FLUX*

(孙印正) (屈爱芳)

Department of Mathematics, Shanghai Normal University, Shanghai 200234, China E-mail: sunyz1742@163.com; afqu@shnu.edu.cn

Hairong YUAN (袁海棠)

School of Mathematical Sciences and Shanghai Key Laboratory of Pure Mathematics and Mathematical Practice, East China Normal University, Shanghai 200241, China E-mail: hryuan@math.ecnu.edu.cn

Abstract We consider the singular Riemann problem for the rectilinear isentropic compressible Euler equations with discontinuous flux, more specifically, for pressureless flow on the left and polytropic flow on the right separated by a discontinuity x = x(t).We prove that this problem admits global Radon measure solutions for all kinds of initial data.The over-compressing condition on the discontinuity x=x(t) is not enough to ensure the uniqueness of the solution.However, there is a unique piecewise smooth solution if one proposes a slip condition on the right-side of the curve x = x(t)+0, in addition to the full adhesion condition on its left-side.As an application,we study a free piston problem with the piston in a tube surrounded initially by uniform pressureless flow and a polytropic gas.In particular,we obtain the existence of a piecewise smooth solution for the motion of the piston between a vacuum and a polytropic gas.This indicates that the singular Riemann problem looks like a control problem in the sense that one could adjust the condition on the discontinuity of the flux to obtain the desired flow field.

Key words compressible Euler equations; Riemann problem; Radon measure solution;delta shock; discontinuous flux; wave interactions

1 Introduction

For many applications in mathematical analysis and physical modeling,considerable attention has been paid to the Euler equations.The one dimensional isentropic compressible Euler equations read as

for (x,t)∈R×[0,∞), andρstands for the mass density,ufor the velocity, andpfor the pressure.For a two-phase flow consisting of pressureless flow and polytropic flow separated by a free boundaryx=x(t), the state equation can be written as

where 1＜γ ＜3 for most gases is the adiabatic exponent.If there is concentration of mass onx=x(t), that is called a delta shock.Since the flux is discontinuous along the curvex=x(t), system (1.1), together with (1.2), comprises a typical system of conservation laws with a discontinuous flux.

So far,much effort has been devoted to studying conservation laws with discontinuous flux.This is especially so for the scalar case, on account of its applications to a wide range of fields including traffic flow, the sedimentation of suspensions, elasticity, multi-phase flow in porous media, polymer flooding, etc.A feature of these works is that the discontinuity of the flux is fixeda priori.More precisely,researchers have focused mainly on the Cauchy problem of scalar equations like

whereF(x,u) =H(x)f(u)+(1-H(x))g(u), and whereH(x) is the Heaviside function.The existence of weak solutions has been obtained by various methods, including, for example,vanishing viscosity,front tracking,and numerical schemes.These weak solutions are,in general,Lebesgue integrable functions; see [1-3, 5, 6, 13] and the references cited therein.Recently Aektaet al.[3]established a solution of the scalar conservation law(1.3)with this concentration supported on a fixed discontinuity of flux.Fewer results for the system of conservation laws with discontinuous flux have been obtained.Fazio and LeVeque[9], and LeVeque[17, section 14.14],discussed a multifluid problem for non-isentropic compressible Euler equations by numerical simulation, where the interface between two distinct polytropic gases is a contact discontinuity.Readers may catch a glimpse of the system of conservation laws with discontinuous flux in[12, 16, 27].As far as we know, there is no result on the discontinuous flux problem for isentropic flow with concentration.

Usually,the failure of strict hyperbolicity of the system in some regions may lead to the loss of the spatial total variation bound for some conserved quantities, which makes the problem sophisticated.For example, the adhesion property of the pressureless flow may lead to mass concentration.To characterize the concentration phenomenon of system (1.1), one needs an appropriate definition of a measure solution rather than a Lebesgue integrable weak solution.On the other hand, choosing an appropriate entropy condition to deal with the non-uniqueness of weak solutions is also a thorny issue.Several criteria have been proposed for this, depending on the flux function; see,for example,[4,7,11,29].Among these criteria,the over-compressing condition is usually used in the construction of solutions with concentration for other conservation laws [22].A delta shock of (1.1), (1.2) is said to satisfy the over-compressing condition,if

whereul(t)=u(x(t)-,t),ur(t)=u(x(t)+,t), and wherex=x(t) is the delta shock front.

Recently,Jin,Qu and Yuan[15]studied the singular Riemann problem for the Euler system of polytropic gases.They admitted the Radon measure solution proposed by Qu, Yuan and Zhao [25] for a steady Euler system with a general state equation, which generalizes previous definitions of measure solutions of the Euler system for the pressureless case, and they constructed non-unique piecewise constant solutions of the classical Riemann problem under the over-compressing condition, as well as certain existence results for singular Riemann problems.The discontinuity of the flux that might support concentration is determined together with the gas [18]; see [10, 14, 23-26] for more physical background.This means that one needs to propose new criteria on the discontinuity of the flux in order to ensure a unique solution.

In this paper, we consider the singular Riemann problem for the conservation laws with discontinuous flux(1.1), (1.2).The initial data for the singular Riemann problem is formulated as

whereρ0is a nonnegative number.Notice that the singular Riemann problem(1.1),(1.2),(1.6)is consistent with the classical Riemann problem in the caseρ0=u0= 0, while it is totally different in the caseρ0＞0.To study this singular Riemann problem, we admit the concept of a Radon measure solution of the Euler system.Besides the global existence of infinite solutions of the classical Riemann problem satisfying the over-compressing condition (1.5) for any initial left and right states, we also establish the global existence of infinite solutions forρ0＞0 with any initial left and right states under the over-compressing condition (1.5).To get the unique solution, we introduce some new criteria on the discontinuity of the flux based on the natural connection of the singular Riemann problem and the piston problem (cf.[10]); that is, we have the following:

Sticking and Slipping Condition (abbreviated as SS condition): when the pressureless gas flows into the delta shock, it sticks to the delta shock and becomes a part of it, while the polytropic gas on the right of the delta shock has the same speed as it.

We obtain the unique local piecewise smooth solution as well as its clear geometrical structure under the SS condition for a large range of initial data.The global existence of such solutions is considered in a future work.For initial data not in the relevant range, further exploration is required, for various technical reasons.

As an application of the singular Riemann problem, we consider a free piston problem.Initially, there is a free piston with massρ0and velocityu0, and it separates the uniform pressureless gas on the left from the uniform polytropic gas on the right.The piston is accelerated by the difference of the forces acting on each side.We prove that the existence of this piston problem can be reduced to the existence of a singular Riemann problem, and therefore we get the local existence of a piecewise smooth solution of the piston problem.

For the free piston problem with more general initial data, Liu [20] obtained a global solution with a small bounded variation by studying two boundary value problems of the one dimensional full Euler equations in Lagrangian coordinates, coupled with an ordinary differential equation satisfied by the piston.Takeno [28] considered a free piston problem for onedimensional isentropic gas dynamics, with the state equation on each side of the piston being a different polytropic gas, by the method of compensated compactness.More results on piston problems can be found in the review article of Ding and Li [8].

The main contributions of this paper include, first, showing that the discontinuity of the flux is free, which is determined together with the solution, rather than being fixeda priorias was done in previous works.Second, the existence of multiple solutions satisfying the over compressing condition for the singular Riemann problem is demonstrated, and solutions with more abundant wave structures are found, in particular, the structure composed of a delta shock and a rarefaction wave.Third, the interaction of a rarefaction wave and a delta shock is analyzed.Fourth, we propose an additional physical boundary condition on the discontinuity of the flux function to obtain the unique solution; this has applications for studying classical piston problems.Finally, we establish a direct relation between the singular Riemann problem and the classical fluid-structure coupling problem, and get the local existence as well as the structure of a classical piston problem.

The organization of the rest of this paper is as follows: in Section 2,we propose a definition of Radon measure solutions for the Riemann problem of the conservation laws with discontinuous flux (1.1), (1.2), (1.6).The generalized Rankine-Hugoniot conditions of the delta shock are also derived.In Section 3, we construct the Radon measure solutions of the Riemann problem(1.1), (1.2), (1.6) withρ0=0; these consist of a delta shock and classical waves in a polytropic gas.The structure of solutions depends on the relations of the initial states and whether the over-compressing condition (1.5) or the SS condition is under consideration.Solutions consisting of three waves are also considered.In Section 4, we focus onρ0＞0.Because of the initial mass concentration, we have to tackle the problem of the interactions of delta shocks and classical waves, especially rarefaction waves, and thus consider the existence of compound waves.Whether these solutions satisfy the over-compressing condition is also verified.In Section 5,under the SS condition, by regarding the delta shock as a free boundary, the local existence of a unique piecewise smooth solution is established.As an application of the singular Riemann problem, we consider, in the end, some related free piston problems, which leads to the equivalence of delta shocks and free pistons.We briefly summarize the results and propose some unsolved problems in a short Section 6.

2 Definition of Radon Measure Solutions and Delta Shock

We now present the definition of Radon measure solutions for the Riemann problem (1.1),(1.2), (1.6).

2.1 Definition of Radon Measure Solutions

LetL1be the Lebesgue measure, andM(R) the space of Radon measures on the real line R.Consider a mapping

is continuous fort.We denote the collection of all these mappings byC([0,∞);M(R)).In particular, we say thatm(t) is a Dirac measure with weightωL(t) supported on a Lipschitz curveL.={x=x(t)|t ∈[0,T)}, and denoted specifically asωL(t)δx(t), ifωL(t) is continuous,and if

In the sequel,C1candCcdenote, as usual, the set of continuously differentiable and continuous functions with compact supports, respectively.The derivative of a functionφ(x,t)with respect totis written asφt, and similarly,φx.=∂xφ.We also use the standard notationm ≪ϱto mean that the measuremis absolutely continuous with respect to the measureϱ.

Definition 2.1 Letϱ ∈C([0,∞);M(R)), and letu(·,t) be aϱ(t)-measurable function on R for allt ≥0.The pair (ϱ,u) is called a Radon measure solution of the Riemann problem(1.1), (1.2) and (1.6) if there existm,n,℘∈C([0,∞);M(R)) such that

1) for any test functionφ ∈C1c(R2), it holds that

3) the classical Lax entropy condition is valid for all discontinuities in the flow field (ρ,u)in the space-time region, whereϱ(t)≪L1.

Obviously, if(ϱ(t),u(·,t))is a Radon measure solution to the Riemann problem(1.1), (1.2)and (1.6), then the initial data (1.6) should be written rigourously as

whereL1is the Lebesgue measure restricted on anL1-measurable setA, and IAis the indicator function of the setA.

2.2 Delta Shock

We call a Radon measure solutiona delta shockif it is of the form

with Ωl.={x ∈R|x ＜x(t)}, Ωr.={x ∈R|x ＞x(t)},x(0) = 0, and where (ul,ρl) (resp.(ur,ρr)) is a smooth solution of (1.1) in Ωl(resp.Ωr) with the state functionp= 0 (resp.p(ρ) =ργ).We now consider the Radon measure solutions such that the initial left state and right state are connected by only a single delta shock.Whether these solutions satisfy the over-compressing condition (1.5) or the SS condition is to be verified.

As usual,we start with the generalized Rankine-Hugoniot conditions along the discontinuity of the flux and get the delta shock curve.By substituting(2.9)into(2.4),we obtain the following jump conditions along the discontinuityx=x(t):

Here [ρ].=[ρ](x(t),t)=ρ(x(t)+,t)-ρ(x(t)-,t).Hence, we have that [ρ]=ρr-ρl.These four equations in (2.10), together with the Radon-Nikodym derivatives’ relations (2.5),

Then, the delta shock is determined and given by (2.12) and (2.13), once the front of delta shockx=x(t) is solved.

We go on to determine the curvex=x(t).Equations (2.11) and (2.13) give that

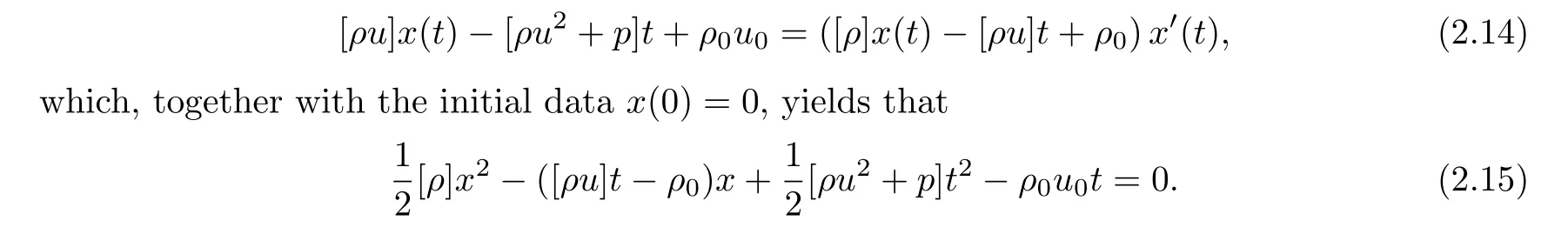
One may refer to [15, Lemma 2] for more detailed calculations, though keep in mind that here the coefficient of[ρ]inaispr,rather than[p],as it is in that paper.This difference creates a big difference in the analysis.

Now, we have the following conclusion regarding the existence ofx=x(t):

Lemma 2.2 Under the condition thatwρ(t), given by (2.13)1, is nonnegative, we have the following solvability conclusion regarding the equation (2.15) with respect tox(t):

It follows from this lemma that, for the Riemann problem (1.1), (1.2), (1.6), ifρ0=0, the delta shock front is a straight line.For [ρ]=0, the difference of pressure only affects the speed of the wave, and the difference of speed affects both the weight and the speed of the wave.For[ρ]/=0, both the speed and the weight of the wave depend on all of the initial data.

The proofs of these two lemmas can be obtained by some tedious and straightforward calculations similar to those presented in [15, Lemma 2, Propositions 1, 2, 3] (with some minor modifications), so we omit them here.Special attention should be given to the case [ρ] = 0,[u]=0 andρ0=0, which makes the equation (2.14) unsolvable; that is, the solution consisting only of a single delta shock does not exist due to the pressure of the polytropic gas.This is another difference from [15].The main results of Lemmas 2.3 and 2.4 are illustrated in Table 1.

Remark 2.5 Fix(ul,ρl)withρl ≥0.In view ofa(ul,ρl;u,ρ)=ρlρ(u-ul)2-ργ(ρ-ρl),it is easy to check that

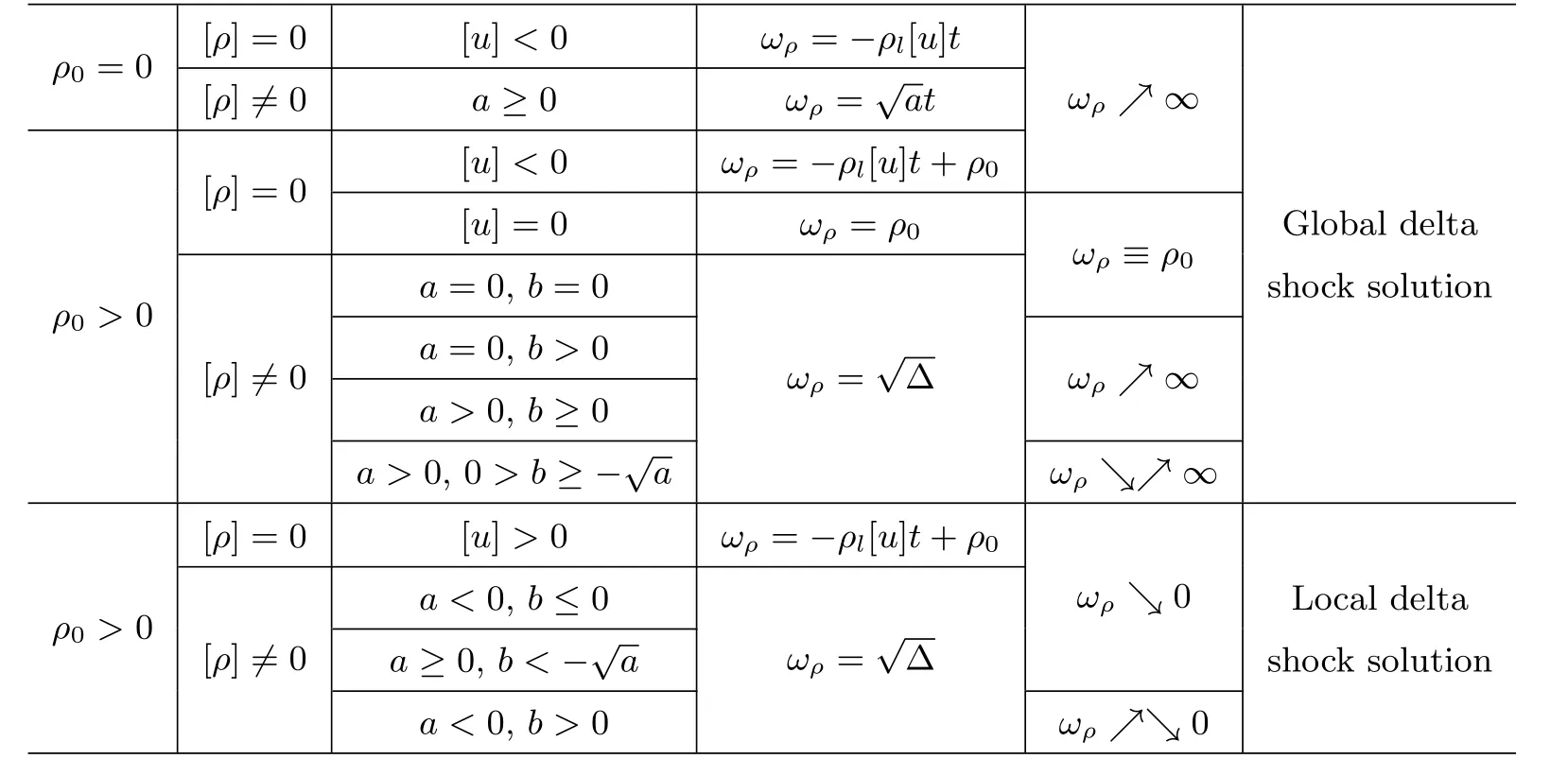
Table 1 Delta shock solution

For the classical Riemann problem (ρ0= 0), it follows from (2.18) that, forρl= 0, the curvea= 0 reduces to theu-axis.Forρl ＞0, the monotonicity and convexity of these two curves can be analyzed by standard differentiation.

As shown in Lemmas 2.3 and 2.4,for a given initial left stateUlin the phase(u,ρ)-plane,the domain to whichUrbelongs such that the solution of the classical Riemann problem consists of a single delta shock is the region{(u,ρ)|a ≥0}{ρ=ρl,u ＞ul}.Meanwhile, for the singular Riemann problem, whenUrbelongs to a portion of the region{(u,ρ)|a ≥0}, the delta shock exists globally.Otherwise, the delta shock exists locally.This feature may lead,significantly, to the possibility of multi-solutions in the construction.Additional conditions,according to certain physical mechanisms, should be proposed in order to ensure a unique solution.In the sequel, we will see that to construct a global solution to the singular Riemann problem without any additional condition on the delta shock is straightforward.Once extra conditions are proposed on the delta shock, however, the problem becomes quite complicated.We will discuss the problem under respectively the over-compressing condition (1.5) and the SS condition.

2.2.1 Discontinuity of Flux That Satisfies the Over-compressing Condition (1.5)

In what follows, we check the over-compressing condition (1.5) for the delta shocks constructed in Lemmas 2.3 and 2.4.Note thatbcan be rewritten as

Thus, a necessary condition for the over-compressing (1.5) is thatb ≥0.That is to say, whenb ＜0, the over-compressing condition (1.5) initially fails.Also,asatisfies that

Then,a ≤ρ2r[u]2when [ρ]≥0, anda ≥ρ2r[u]2when [ρ]≤0.By the relations amongx′(t),ulandur, we then have

Lemma 2.6 Considering the Radon measure solutions of the singular Riemann problem(1.1), (1.2) and (1.6) obtained by Lemmas 2.3 and 2.4, we have the following results:

1) forρ0=0, the solutions obtained by Lemma 2.3 satisfy the over-compressing condition(1.5) if one of the following conditions is satisfied:

(i) [ρ]=0, [u]≤0,pr ≤ρl[u]2,

(ii) [ρ]＞0, [u]≤0,a ≥ρ2l[u]2,

(iii) [ρ]＜0, [u]≤0, 0≤a ≤ρ2l[u]2;

2) forρ0＞0, the solutions obtained by Lemma 2.4 satisfy the over-compressing condition(1.5) globally if one of the following conditions is satisfied:

(i) [ρ]=0,ur ≤u0≤ul,pr ≤ρl[u]2,

(ii) [ρ]＞0,ur ≤u0≤ul,a ≥ρ2l[u]2,

(iii) [ρ]＜0,ur ≤u0≤ul, 0≤a ≤ρ2l[u]2;

3) forρ0＞0, the solutions obtained by Lemma 2.4 satisfy the over-compressing condition(1.5) locally if one of the following conditions is satisfied:

(i) [ρ]=0,ur ≤u0≤ul,pr ＞ρl[u]2,

(ii) [ρ]＞0,ur ≤u0≤ul,a ＜ρ2l[u]2,

(iii) [ρ]＜0,ur ≤u0≤ul,a ＞ρ2l[u]2.

Lemma 2.6 implies that the curvea=ρ2l[u]2in the phase (u,ρ)-plane also plays an important role in constructing solutions; this will be specified in Subsection 3.2.

2.2.2 Discontinuity of Flux That Satisfies SS Condition

We go on to check the SS condition for the delta shocks constructed in Lemmas 2.3 and 2.4.We have the following conclusions:

Lemma 2.7 (1)Forρ0=0,the problem(1.1),(1.2)and(1.6)admits a global delta shock with the discontinuityx=x(t) satisfying thatx′(t)=urif and only if

Proof (1) Assume that the initial left and right states are connected by a single delta shockx=x(t).For the classical Riemann problem, that is,ρ0=0, when [ρ]=0, [u]≤0, and by (2.16), the relationx′(t)=urgives that

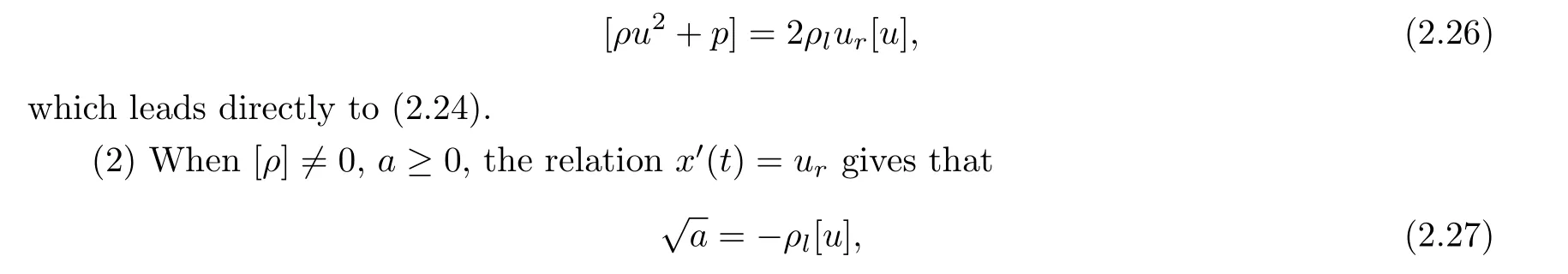
withur ≤ul.By replacing the expressionadefined in (2.18), we have that

3 Radon Measure Solutions of the Classical Riemann Problem (ρ0 =0)

In this section, we investigate the Radon measure solutions of the classical Riemann problem (1.1), (1.2) and (1.6), that is,ρ0= 0, for general initial left and right constant data(ρl,r,ul,r).As is shown in Section 2, the initial left and right constant states cannot always be connected by just a single delta shock globally, or even locally.To construct the solution, more elementary waves should be taken into account.We search now for solutions with elementary waves connected by constant states.Notice that the flow on the left of the discontinuity of the flux is pressureless, while it is a polytropic gas on the right.Recall that for the pressureless gas, the elementary waves are a contact discontinuity and a delta shock; for the polytropic gas,the elementary waves are the classical shock wave, the rarefaction wave and the delta shock,as indicated in [15].Since this still lacks a general entropy condition to ensure the unique solution, we search for the solutions with the least number of waves in the construction of the Riemann problem first for all initial data.Also, we will give some examples which show that,for some initial data, there exist multiple solutions consisting of different numbers of waves.As mentioned above, the over-compressing condition (1.5) and the SS condition are addressed to ensure uniqueness in the construction of solutions consisting of delta shocks.We will further pick up those solutions under either of these two conditions.

3.1 Multi-solution of the Classical Riemann Problem

Lemma 2.3 shows that, when the initial dataUl,rsatisfies one of (i) [ρ] = 0, [u]＜0; (ii)[ρ]＜0; (iii) [ρ]＞0,a ≥0, it can be connected by the discontinuity of the flux with the concentration of mass and momentum.What left is to consider the cases (iv) [ρ]＞0,a ＜0;(v) [ρ]=0, [u]≥0.Recall that (see the appendix in [15]), for the polytropic gas, the set of left states that can be connected to the right stateUrby a forward shock or a forward rarefaction wave in state space are, respectively,

We consider first the case for the initial data satisfying that [ρ]＞0,a ＜0.We seek solutions that consist of a delta shock followed by an elementary wave in polytropic flow, and state the following:

Lemma 3.1 Consider the classical Riemann problem (1.1), (1.2), (1.6) withρ0= 0.If the initial states satisfy that [ρ]＞0,a ＜0, then

(i) there exist infinitely many Radon measure solutions consisting of a delta shock followed by a forward rarefaction waveR2;

(ii) constructing Radon measure solutions consisting of a delta shock followed by a forward shockS2is inappropriate;

(iii) neither constructing solutions consisting of a delta shock followed a backward rarefaction waveR1, nor a delta shock followed by a backward shockS1, is appropriate.

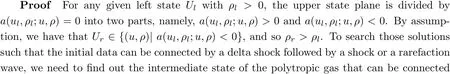
which is consistent with (3.7).

For [ρ]＜0, we can get an inequality (3.7) similar to that for [ρ]＞0.By standard calculations, we solve (3.7) and obtain that

which is unsolvable forρ ＞0, and therefore illustrates our claim.

that is, the curvesC2andD2are tangential atP1.

LetQ1be the domain surrounded by the curvesC1,C2,D1andD2.Then, forUr ∈{(u,ρ)|a(ul,ρl;u,ρ)＜0}, anyUm ∈R-12(Ur)∩(Q1{ρ=ρl,u ≥ul}) can be chosen as intermediate states such thatUlcan be connected toUmby a delta shock andUmcan be connected toUrby a forward rarefaction waveR2.In addition,we may check,without any difficulty,thatx′(t)≤λ2(Um) whenρm=0,um ≥ul; see Figure 1.

Figure 1 When Ur ∈{(u,ρ)|a ＜0}, there exist Radon measure solutions consisting of a delta shock followed by a forward rarefaction wave R2, with the intermediate states being in the region surrounded by C1, C2, D1 and D2, as well as the u-axis.While constructing a solution consisting of a delta shock and a forward shock S2, is inappropriate.

At the end of the proof, we show the inappropriateness of constructing solutions consisting of a delta shock followed by a backward shockS1forUr ∈{(u,ρ)|a(ul,ρl;u,ρ)＜0}.Assume,to the contrary, thatUlcan be connected to an intermediate stateUmby a delta shock and thatUmcan be connected toUrby a backward shockS1.Then

which contradicts (3.24).Then, we claim that the curvesD′1andD′2must be in the interior of the region{(u,ρ)|a(ul,ρl;u,ρ)＜0}, which implies that solutions consisting of a delta shock and a backward shockS1do not exist because of the non-existence of admissible intermediate states.This completes the proof.□

Consider now the case for the initial data satisfying that [ρ] = 0, [u]≥0.We go on to seek singular Riemann solutions that consist of a delta shock followed by elementary waves in a polytropic flow.We have the following conclusions:

Lemma 3.2 Consider the classical Riemann problem (1.1), (1.2), (1.6) withρ0= 0.If the initial states satisfy that [ρ]=0, [u]≥0, then

(i) there exist Radon measure solutions consisting of a delta shock followed by a forward rarefaction waveR2;

(ii) there exist Radon measure solutions consisting of a delta shock followed by a backward rarefaction waveR1;

(iii)neither constructing solutions consisting of a delta shock followed by a backward shockS1nor a delta shock followed by a forward shockS2is appropriate;

(iv) there exist Radon measure solutions with three waves.

Proof (i) For givenUl,rsatisfying that [ρ]=0, [u]≥0, these two states can be joined by a delta shock and a forward rarefaction waveR2.In fact, for anyUm ∈R-12(Ur)∩(Q1∪{ρ=0,u ≥ul}),Ulcan be connected toUmas above by a delta shock, andUmcan be connected toUrby a forward rarefaction waveR2; see Figure 2.More precisely, assume that the forward rarefaction wave curveR2(ul,0) passes through (ul,0) on the left, and intersects the curve{ρ=ρl,u ≥ul}at ～U=(～u,ρl), where

Then, ifur ≥～u, the left stateUlis in fact connected uniquely to the intermediate stateUm=(um,0) by a contact discontinuity, which can be regarded as a delta shock with a weight of zero.Ifur ＜～u, the intermediate statesUmare neither vacuums, nor unique.

Figure 2 When the initial states satisfy[ρ]=0,[u]≥0,there exist Radon measure solutions consisting of a delta shock followed by a forward rarefaction wave R2,with the intermediate states being in the region surrounded by C1, C2, D1 and D2, as well as the u-axis.

(ii) To construct solutions consisting of a delta shock followed by a backward rarefaction waveR1, similarly to Lemma 3.1, we determine the region to which the intermediate stateUmbelongs by proving thatx′(t)≤λ1(Um), whereλ1=u-c.

Figure 3 When the initial states satisfy[ρ]=0,[u]≥0,there exist Radon measure solutions consisting of a delta shock followed by a backward rarefaction wave R1, with the intermediate states being in the region surrounded by C1, C2, D3 and D4.

(iii) Suppose, to the contrary, thatUmis an intermediate state such thatUlis connected toUmby a delta shock andUmis connected toUrby a forward shockS2.Then

which contradicts (3.34).Therefore, there is no solution consisting of a delta shock and a forward shockS2because of the non-existence of an admissible intermediate state.

(iv) It is easy to check that when the initial states satisfy that [ρ]=0 and [u]≥0, we can choose a statem ∈R-12(Ur) such thatUlandare connected by a delta shock followed by a backward rarefaction waveR1, andmis connected toUrby a forward rarefaction waveR2;that is, this solution contains three waves; see Figure 4.This completes the proof.□

Figure 4 Solutions with three waves can be constructed by choosing the intermediate state Um as belonging to the region Q2, which is surrounded by curves C1, C2, D3 and D4.

Note that, so long as the intermediate stateUmthat we have chosen belongs to the regionQ2, solutions containing three waves can be constructed for general initial data rather than satisfying that [ρ] = 0, [u]≥0.This fact also implies that the statesUlandcan be connected by a delta shock followed by a backward rarefaction waveR1as well, in addition to the single delta shock constructed in Lemma 2.3.

Remark 3.3 Ifρl= 0, the curve{(u,ρ)|a(ul,ρl;u,ρ) = 0}degenerates to theu-axis.Lemma 3.1 implies that there exists a unique Radon measure solution consisting only of a forward rarefaction waveR2for the classical Riemann problem (1.1), (1.2), (1.6) withρ0= 0 andρr ＞0.

Combining Lemmas 2.3, 3.1, 3.2, we arrive at

Theorem 3.4 The classical Riemann problem(1.1),(1.2),(1.6)withρ0=0 admits global solutions forul,ur ∈R andρl,r ≥0.Moreover, we have that

(i)when the initial dataUl,rsatisfies one of(a)[ρ]=0,[u]＜0;(b)[ρ]＜0;(c)[ρ]＞0,a ≥0,then there exists a solution consisting only of the discontinuity of the flux with concentration of mass and momentum(i.e., delta shock).There also exist infinitely many solutions consisting of a delta shock followed by a backward rarefaction waveR1for (a) and (b);

(ii) when the initial states satisfy that [ρ] = 0, [u]≥0, then there exist infinitely many Radon measure solutions consisting of a delta shock followed by a forward rarefaction waveR2,or of a delta shock followed by a backward rarefaction waveR1.Solutions consisting of three waves can be constructed as well;

(iii) when the initial states satisfy that [ρ]＞0,a ＜0, then there exist infinitely many Radon measure solutions consisting of a delta shock followed by a forward rarefaction waveR2.

3.2 Multi-solution Under Over-compressing Condition

As indicated by Theorem 3.4,the uniqueness of a solution to the classical Riemann problem is lost, due to the appearance of delta shocks.We go on in this subsection to single out those solutions constructed in Theorem 3.4 that satisfy the over-compressing condition (1.5).

For given left state(ul,ρl),we divide the upper(u,ρ)-plane into several parts by the curves defined in Section 2, according to the results of Lemma 2.6.In addition, define that

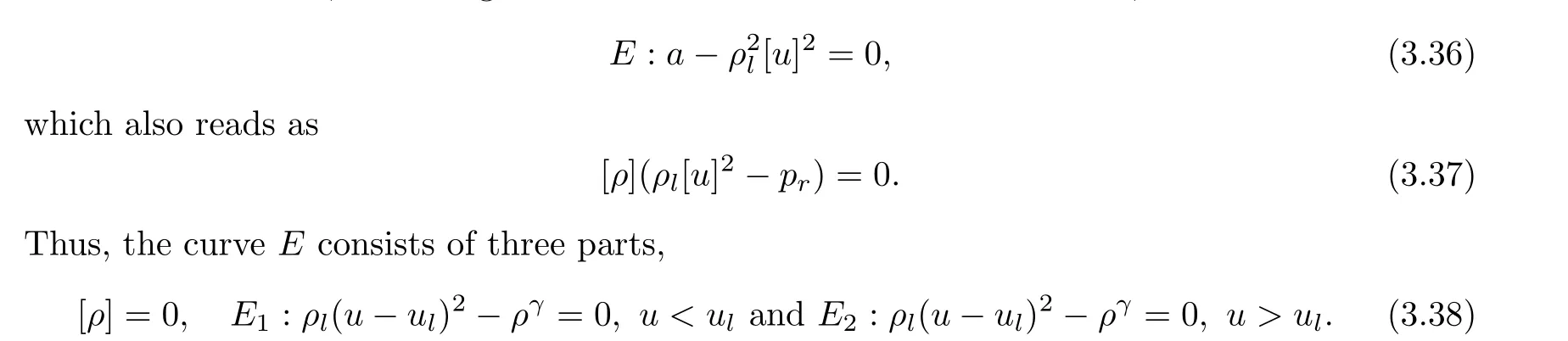
By direct calculations, we obtain that, for a given left stateUlwithρl ＞0, the curvesC1,E1do not intersect whenρ ＞0, and so neither do the curvesC2,E2; see Figure 5.Forρl=0, the curvesC1andE1, as well asC2andE2, coincide, which is consistent with Remark 3.3.

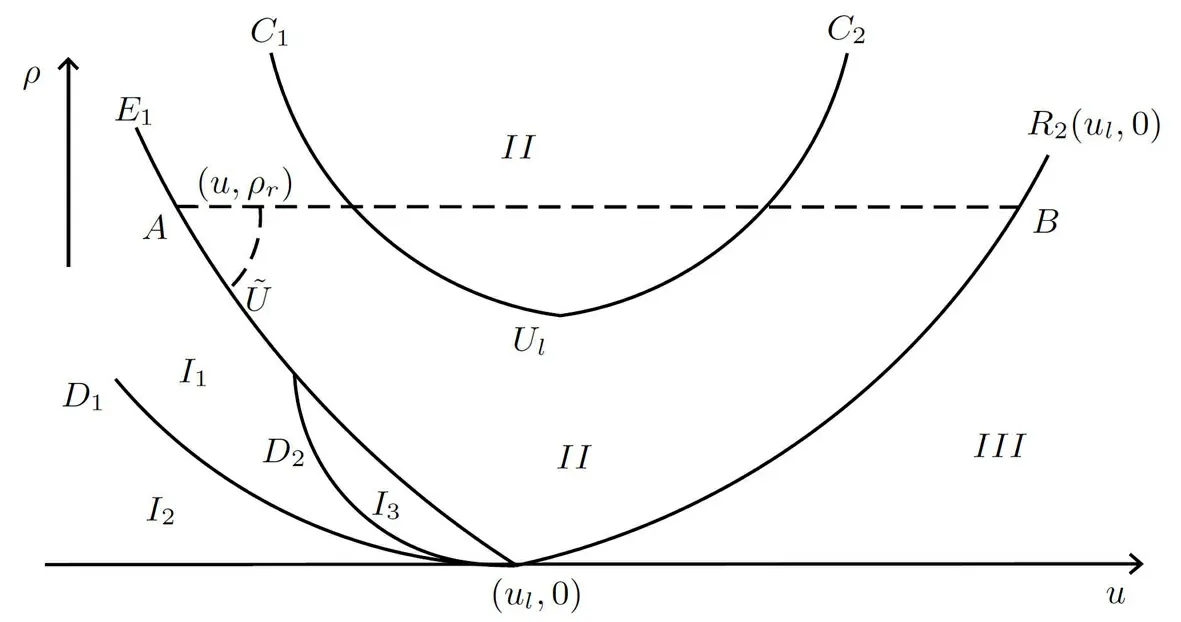
Figure 5 When Ur ∈I, there exists a Radon measure solution consisting of a single delta shock.When Ur ∈II, there exist Radon measure solutions consisting of a delta shock followed by a forward rarefaction wave R2.When Ur ∈III, there exists a unique Radon measure solution consisting of a delta shock followed by a forward rarefaction wave R2.

We introduce some notations for the partitions as follows:

Theorem 3.5 The classical Riemann problem(1.1),(1.2),(1.6),for whichρ0=0,admits global solutions that satisfy the over-compressing condition (1.5) forul,r ∈R andρl,r ≥0.Moreover, we have that

(i) ifUr ∈I, there exists a Radon measure solution consisting of a single delta shock;

(ii) ifUr ∈II, there exist infinitely many Radon measure solutions consisting of a delta shock followed by a forward rarefaction waveR2, with intermediate states lying in I1∪E1;

(iii) ifUr ∈III, there exists a unique Radon measure solution consisting of a contact discontinuity followed by a forward rarefaction waveR2, with the intermediate state being a vacuum.

Proof (i) For the case whenUr ∈I, the results have be proven in Lemma 2.6.

(ii) IfUr ∈II, we now show the conclusion by constructing solutions consisting of a delta shock followed by a forward rarefaction waveR2.For the curveE1, we have that

By continuity, the curvesE1andR-12(u,ρr) must intersect at a unique point ～U.It is easy to check thatx′(t)≤～u+～c.This implies the existence result in region II.

We now determine the region to which the intermediate stateUmbelongs,under the further requirement thatx′(t)≤um+cm.As was discussed in Lemma 3.1, this region is precisely that surrounded by the curvesD1andD2in region I.Solving the equations

so that these solutions satisfy the over-compressing condition (1.5) as well.□

Remark 3.6 The proof of the above theorem also implies that under the over-compressing condition (1.5), the structure of the classical Riemann solution is unique, in the sense that the solutions consist of the same types of waves,but these may differ from each other in terms of the strength of the corresponding waves, so that the intermediate state of the solution may be nonunique.In addition, solutions with three waves do not exist here, since the over-compressing condition(1.5)rules out the possibility of wave structures that consist of a delta shock followed by a backward wave in the polytropic flow.

3.3 Unique Solution Under SS Condition

In this subsection,we continue to consider the classical Riemann problem(1.1),(1.2),(1.6)withρ0=0, and present the following conclusion:

Theorem 3.7 Under the SS condition, the classical Riemann problem (1.1), (1.2), (1.6)withρ0= 0 admits a unique global Radon measure solution consisting of waves that connect piecewise constant states.More precisely,

(i) ifUr ∈E1, there exists a unique Radon measure solution consisting of a single delta shock;

(ii) ifUr ∈I, there exists a unique Radon measure solution consisting of a delta shock followed by a forward shockS2;

(iii) ifUr ∈II∪III, there exists a unique Radon measure solution consisting of a delta shock followed by a forward rarefaction waveR2.

Proof For any given left stateUl, denote that

which is precisely the curveE1defined in (3.38).Then the curveF(Ul) andR2(ul,0) divide the upper-half state plane into the same three parts as those specified in (3.39).

IfUr ∈F(Ul), it follows from Lemma 2.7 thatUrcan be connected to the left stateUlby a delta shockx=urt.

IfUr ∈I, the forward shock curveS-12(Ur) viaUron the right will intersect withF(Ul) at a unique point (um,ρm).Thus,Ulcan be connected toUmby a delta shockx=umt, whileUmcan be connected toUrby a forward shockS2.

IfUr ∈II, the forward rarefaction wave curveR-12(Ur) viaUron the right will intersect withF(Ul) at a unique point (um,ρm).Thus,Ulcan be connected toUmby a delta shockx=umt, whileUmcan be connected toUrby a forward rarefaction waveR2.

IfUr ∈III, the curveR-12(Ur) viaUrwill intersect with theu-axis at a unique pointUm= (0).Thus,Ulcan be connected to the vacuum stateUmby a contact discontinuityx=ult, whileUmcan be connected toUrby a forward rarefaction waveR2.□

4 Multi-solution of the Singular Riemann Problem under Over-compressing Condition

In this section, we consider the singular Riemann problem (1.1), (1.2), (1.6) withρ0＞0.We first restrict ourselves to the solution with waves connected by constant states.Under the over-compressing condition(1.5)on a delta shock,we find that there is no solution consisting of waves connected by constant states for some initial data.Solutions with more abundant wave structures should be taken into consideration.

4.1 Global Solutions with Waves Connecting Piecewise Constant States

Note that we can always construct a local delta shock for the singular Riemann problem withρ0＞0 which can be prolonged; we can do this by solving a classical Riemann problem withρ0= 0 at the time when the delta shock disappears.We have the following result about the existence of Radon measure solutions:

Theorem 4.1 The singular Riemann problem (1.1), (1.2), (1.6) admits infinitely many global Radon measure solutions, the structure of which near the origin consists only of a delta shock.

Figure 6 Global delta shock

Figure 7 [ρ]=0, [u]＞0

Figure 8 [ρ]＞0, a ＜0

Figure 9 [ρ]/=0, a ＞0, b ＜-

By Theorem 3.4 and Theorem 4.1, we know that the singular Riemann problem admits infinitely many solutions.Next, as was done in Section 3 forρ0=0, we would like to construct solutions satisfying the over-compressing condition (1.5).Then, interactions between the delta shock and the classical waves are inevitable.

4.2 Multi-solution Under Over-compressing Condition

In this subsection, we mainly consider the singular Riemann problem forρ0＞0 under the over-compressing condition (1.5).Depending on the initial states on both sides of the concentration point that satisfies (1.5) or not, we divide the discussion aboutu0≤ur+crinto four cases.Case 1: the initial states satisfy the over-compressing condition (1.5); namely,ur ≤u0≤ul.Case 2:u0≤min{ul,ur}.Case 3:u0≥max{ul,ur}.Case 4:ul ≤u0≤ur.After that, we discuss the caseu0＞ur+cr.

4.2.1 The Initial States Satisfying the Over-compressing Conditionur ≤u0≤ul

Recall that,for any non-vacuum left initial stateUl,the upper state space(u,ρ)-plane is divided into three parts, I, II, III, given in (3.39) by the curvesE1via (ul,0) andR2(ul,0).Moreover,I is divided into three parts too; see Figure 5.Denote by II1the region II∩{u ≤ul}, for simplicity.Asur ≤ul, the initial right stateUrbelongs either to II1or to I.

If the initial data satisfies thatur ≤u0≤min{ul,ur+cr}andUr ∈I,then,by Lemma 2.6,the singular Riemann problem (1.1), (1.2), (1.6) admits a solution consisting only of a single delta shock.It also admits infinitely many solutions consisting of a delta shock and a forward rarefaction waveR2.

Lemma 4.2 Under the over-compressing condition (1.5), with a given left stateUl, ifUr ∈II1andur ≤u0≤min{ul,ur+cr}, then the singular Riemann problem (1.1), (1.2), (1.6)admits infinitely many solutions consisting of a delta shock and a forward rarefaction waveR2,with the constant intermediate stateUm ∈I1satisfying thatum+cm ≥u0; see Figure 10.

Proof ForUr ∈II1,one may find,by Lemma 2.6,an intermediate stateUm ∈R-12(Ur)∩I to get the local solution.The assumption thatur ＜ulimplies thatR-12(Ur)∩I/=Ø.Thus,anyUm ∈R-12(Ur)∩I satisfying thatu0≤um+cmcan be chosen as an intermediate state to connect the left stateUlby a delta shock and the right stateUrby a forward rarefaction waveR2at first.Since the delta shockx=x(t) is no longer straight, we need to check whether it will interact with the rarefaction waveR2later.It is enough to calculate the interaction time ofx=x(t) and the characteristicx=(um+cm)t.Supposing that they interact at some timet, then we have that, if [ρ]=ρm-ρl=0, the interaction timetshould satisfy that

which, combined with (2.19), gives thatt=0, or that,

which is consistent with (4.3) for [ρ]=0.

Sinceu0≤um+cm, the numerator of (4.3) and (4.5) is non-positive.The denominator of(4.3) and (4.5) is non-negative if and only if

It follows from (4.6) that, forUm ∈R-12(Ur)∩I1andu0≤um+cm, the value oftgiven by (4.3) and (4.5) is negative; that is, the solutions consist of a delta shock connectingUlandUm, followed by a forward rarefaction waveR2connectingUmandUr, without any interaction of waves (see Figure 10).This completes the proof.□

Figure 10 Um ∈I1, u0 ≤um+cm

Figure 11 Um ∈I1, u0 ＞um+cm

Under the over-compressing condition(1.5),we consider global solutions in which the delta shock is coupled with a rarefaction wave.

Lemma 4.3 Under the same assumptions as those used in Lemma 4.2, the singular Riemann problem (1.1), (1.2), (1.6) admits infinitely many global solutions.These solutions consist of a compound wave at first, which is the coupling of a delta shock and a forward rarefaction waveR2.In some solutions, these two waves will be separated from each other by an intermediate constant stateUm ∈I1satisfying thatum+cm ≤u0.In some other solutions,this kind of couple will never terminate in finite time, withx′(∞) =u∞+c∞satisfying thatU∞=(u∞,ρ∞)∈D1∪D2and thatu∞+c∞＜u0; see Figures 11 and 12.

Proof For any pointUm ∈R-12(Ur)∩I1, withu0＞um+cm, although there is no local solution with the same structure as that in Lemma 4.2, we can construct a solution by first finding a compound wave of a delta shock and a forward rarefaction wave.

Assume that the front of the delta shock in the compound wave isx=x(t).By the generalized Rankine-Hugoniot conditions (2.10), we have that

whereu+(t),ρ+(t) are defined as in (4.1).Notice that the right side of the delta shock is assumed to be a centred rarefaction wave; it is a system of equations with unknown functionsωρ(t),ωm(t),x(t),u+(t) andρ+(t).We drop all of the subscripts “+”, without confusion.The first two equations of (4.7) yield that

which determines the existence ofρ+(t)in(4.7).The other unknown functions are consequently determined by (4.7).

We now determine the time when the delta shock separates from the rarefaction waveR2.Lettingρ=ρmin (4.17), we obtain that

Therefore, whenUm ∈I1, the timet6above is positive.Whent ＞t6, it becomes a case ofu0＜um+cm, as was discussed in Lemma 4.2.Thus, the delta shock and rarefaction wave are separated by a constant intermediate stateUm; see Figure 11.

As the selection ofUm ∈R-12(Ur)∩I1tends to the boundaryD1andD2, the timet6defined by (4.18)tends to infinity,which implies that the coupling will never terminate in finite time; see Figure 12.□

Figure 12 U∞∈D1 ∪D2,u0 ＞u∞+c∞

Figure 13 Um ∈I2 ∪I3, u0 ≤um+cm

We next search for solutions whereby a delta shock interacts with the forward rarefaction waveR2.

Lemma 4.4 Under the same assumptions as those used in Lemma 4.2, the singular Riemann problem(1.1),(1.2),(1.6)admits infinitely many solutions consisting of a delta shock and a forward rarefaction waveR2.They are separated from each other at first by an intermediate constant stateUm ∈I2∪I3withum+cm ≥u0.After a period of time, they intersect and then interact with each other.This interaction will never terminate in finite time.The solution is illustrated in Figure 13.

Proof For anyUm ∈R-12(Ur)∩(I2∪I3), as in Lemma 4.2, we first to show that there exists an intermediate constant state that connects the pressureless flow on the left by a delta shock satisfying the over-compressing condition and connects the uniform polytropic gas on the right by a forward rarefaction waveR2.We justify that these two waves intersect at a finite time.Similarly to the analysis in Lemma 4.2, the assumption thatur ＜ulimplies that(Ur)∩(I2∪I3)/=Ø.Ifum+cm ≥u0, then both (4.3) and (4.5) are positive, which means that the solutions consisting of a delta shock connectingUlandUm, followed by a forward rarefaction waveR2connectingUmandUr, exist in finite time, and these two waves are away from each other first, but they will intersect at the timet7given by (4.3) or (4.5).When these two waves meet, one must determine the interaction of a delta shock and a forward rarefaction wave.We now turn to solving this problem.

Whent ＞t7, the delta shock and forward rarefaction waveR2interact with each other.By the generalized Rankine-Hugoniot conditions (2.10), the delta shock frontx=x(t) is given by

whereτ=t-t7, and where (u1,ρ1) are the speed and weight of the delta shock att=t7.Similarly to Lemma 4.3, we drop all of the subscripts “+”, without confusion.Then, by (4.7)and (4.8), the first two equations of (4.19) give that

Therefore, the last equation of (4.19) becomes

Note that

which determines the existence ofρ+(t)in(4.19).Consequently, the system of equations(4.19)is solved.

We next check whether this interaction will terminate in finite time.It is enough to calculate the interaction time ofx=x(t) and the characteristic thatx=(um+cm)tfort ＞t7.Lettingρ=ρmandτ=t-t7in the (4.25), above, we have that

which implies that the delta shock does not intersect the characteristic linex=(um+cm)tfort ＞t7, so this interaction will never terminate.The solution is illustrated by Figure 13.□

Lemma 4.5 Under the over-compressing condition (1.5), with a given left stateUl, ifUr ∈II1and the initial velocities of the singular Riemann problem (1.1), (1.2), (1.6) satisfy thatul ≥u0＞ur+cr, then this admits infinitely many solutions consisting of a local delta shock which then can be prolonged by a solution with the singular Riemann initial dataur=u0≤min{ul,ur+cr}.

Proof WhenUr ∈II1,ul ≥u0＞ur+cr,by Lemma 2.6,we construct a local delta shock int ∈[0,t8] such thatur=x′(t8)＜ul, which becomes the case discussed above fort ＞t8.□

Remark 4.6 The Lemmas 4.2-4.5 above show that by choosing a different intermediate stateUm,we can construct solutions with different wave structures for the same initial data.All of these solutions satisfy the over-compressing condition (1.5) on the delta shock.In addition,the proof of Lemma 4.3 implies that, so long as the intermediate stateUmsatisfies thatu0＞um+cm,we can construct such compound wave solutions without the assumption thatu0≥ur.

4.2.2 The Initial States not Satisfying Over-compressing Condition

As discussed in Remark 4.6, whenρl=0, the region I degenerates into theu-axis, and the vacuum stateUm=(,0) must be taken into account, so that whenu0＞, we can construct the compound wave solution as in Lemma 4.3.This fact will be used in the sequel.

Lemma 4.7 Under the over-compressing condition (1.5), for the singular Riemann problem (1.1), (1.2), (1.6), with given left stateUl, if the initial velocity satisfies thatur ≤ul ＜u0,then it admits global solutions consisting of a delta shock,a contact discontinuity and a forward rarefaction waveR2.

Proof For a given right stateUr, assume that the rarefaction wave curveR-12(Ur) in the phase (u,ρ)-plane intersects with theu-axis at (0) defined as above.Thenul ≥ur ≥and the left stateUlandUm= (,0) are connected by a contact discontinuityx=ultin a zero pressure flow, which is denoted byJ.Ifur ≤u0≤ur+cr, the vacuum stateUmand the right stateUrare connected by a delta shockx=x(t) coupled with a forward rarefaction waveR2.Meanwhile, this delta shock will intersect with the contact discontinuityx=ultin finite timet9, at whichu(x(t9)+,t9)≤x′(t9)≤ul.Thus this becomes the case discussed in Section 4.2.1 fort ＞t9;see Figure 14.Note that the solutions of the new singular Riemann problem att=t9constructed as in Section 4.2.1 are actually unaffected by the rarefaction waves connecting on the right of the state (u(x(t9),t9),ρ(x(t9),t9)).

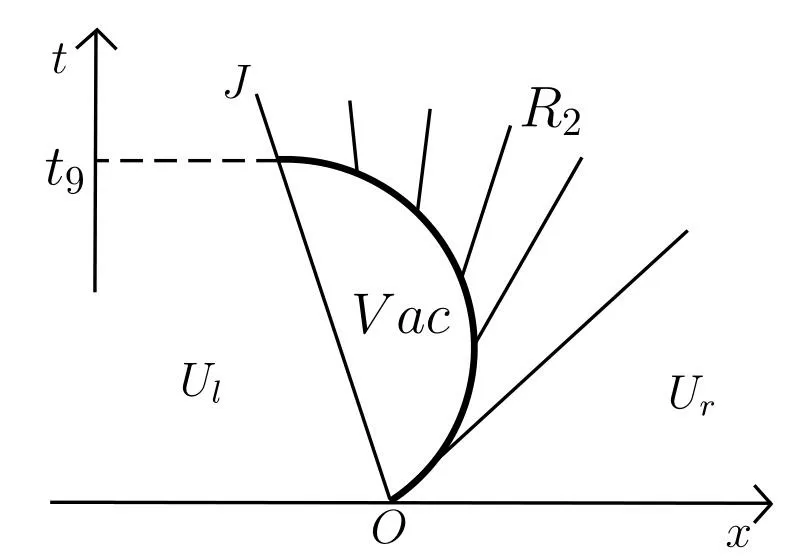
Figure 14 ur ≤ul ＜u0 ≤ur +cr

Figure 15 ur ≤ul ＜u0

Ifur ≤u0, we construct a solution withUmandUrbeing connected by a local delta shockx=x(t) fort ∈[0,t10], where

which implies that the delta shock intersects with the contact discontinuityx=ultbefore the over-compressing condition (1.5) fails.Thus this also becomes the case discussed in Section 4.2.1 after the interaction timet10, sinceur ≤x′(t10)≤ul; see Figure 15.□

Lemma 4.8 Under the over-compressing condition (1.5), for the singular Riemann problem(1.1),(1.2),(1.6),with a given left stateUl,if the initial velocity satisfies thatu0＜ur ＜ul,then it admits global solutions consisting of a delta shock and a forward rarefaction waveR2.

Proof Choosing the intermediate stateUm=(0),if≥u0,sinceul ＞u0,there exists,at least in finite time, a solution consisting of a delta shock connecting the statesUlandUmand a forward rarefaction waveR2connecting the statesUmandUr.The delta shock front is

tends toulast →∞.Thus, as was discussed in Section 4.2.1, the delta shock and the rarefaction wave will intersect with each other in finite time, and this interaction will never terminate, although they do not interact initially; see Figure 13.

Lemma 4.9 Under the over-compressing condition (1.5), for the singular Riemann problem (1.1), (1.2), (1.6), with a given left stateUl, if the initial velocity satisfiesu0≤ul ≤ur,then it admits global solutions consisting of a delta shock and a forward rarefaction waveR2.

Lemma 4.10 Under the over-compressing condition(1.5),for the singular Riemann problem (1.1), (1.2), (1.6), with given left stateUl, if the initial velocity satisfies thatul ＜u0≤ur,then it admits global solutions consisting of a delta shock,a contact discontinuity and a forward rarefaction waveR2.

Figure 16 u0 ＜

Figure 17 ul ≤ ≤u0

Lemma 4.11 Under the over-compressing condition(1.5),for the singular Riemann problem(1.1),(1.2),(1.6),with a given left stateUl,if the initial velocity satisfies thatul ＜ur ＜u0,then it admits global solutions consisting of a delta shock,a contact discontinuity and a forward rarefaction waveR2.

By the discussion above, combining Lemmas 2.6 and 4.2-4.11, we arrive at the following conclusion:

Theorem 4.12 Under the over-compressing condition (1.5), the singular Riemann problem (1.1), (1.2), (1.6) admits global Radon measure solutions for any initial data.These solutions are comprised of a delta shock followed by or coupled with a forward rarefaction waveR2if the initial data satisfies thatu0≤ul,while they comprise a delta shock followed by or coupled with a forward rarefaction waveR2and a contact discontinuity if the initial data satisfies thatu0＞ul.

Based on the analysis above,we give a corollary on a special case where the initial left state is a vacuum, which admits simpler wave structures.

Corollary 4.13 Under the over-compressing condition(1.5), the singular Riemann problem(1.1),(1.2),(1.6)withρ0＞0,ρl=0,ρr ＞0 admits global Radon measure solutions.More precisely,

(i) ifu0≤the unique Radon measure solution consists of a global delta shock followed by a forward rarefaction waveR2, with the intermediate state being a vacuum;

(iii)ifu0＞ur+cr,the Radon measure solutions consist of a local delta shock fort ∈[0,t5]and a delta shock coupled with a rarefaction waveR2fort ＞t5.

5 Unique Solution under the SS Condition and an Application to the Piston Problem

As shown above, the over-compressing condition is not enough to single out a unique solution foru0＞.Thus, we would like to seek solutions under the SS condition.As an application, we will illustrate the equivalence of the singular Riemann problem and a free piston problem by showing that the front of the delta shock and the trajectory of the piston are the same.Thus one could, for simplicity, use the former to solve the latter.

5.1 Piecewise Smooth Solutions to the Singular Riemann Problem Under the SS Condition

Lemma 2.7 implies that, generally, there is no solution with constant states connected by a delta shock, due to the arbitrariness ofu0.One needs to seek piecewise smooth solutions for this singular Riemann problem.

Consider the caseu0≤with (,0) being the intersection ofR-12(Ur) and theu-axis.Iful ＜u0, there exists a global solution consisting of a contact discontinuityx=ultin a pressureless flow, a delta shock with the states on both sides of it being vacuums, and a forward rarefaction waveR2connecting the vacuum state on the left and polytropic gasUron the right.This solution is illustrated in Figure 16.

Iful ≥u0, there exists, at first, a solution consisting of a delta shockx=x(t) connecting the pressureless flowUland the vacuum state and a forward rarefaction waveR2connecting the vacuum state and the polytropic gasUr.The velocity of this delta shock satisfies that

Therefore, whenul ≤this solution is global, as is illustrated in Figure 10, withUmbeing a vacuum.Whenul ＞, this delta shock overtakes the forward rarefaction wave at

After timet11, it becomes the case thatu0＞, and the initial state is non-constant; this is complicated, and will be discussed in the future.We have therefore proved the following:

Lemma 5.1 Under the SS condition, the singular Riemann problem (1.1), (1.2), (1.6)admits a unique global piecewise smooth solution for max{ul,u0} ≤, and a local piecewise smooth solution foru0≤＜ul.

and thus is uniquely determined.

Define an angular domain

withg(t)=(u1+c1)tandδbeing a sufficiently small positive constant.

Now,the matter of determining a local classical solution of the singular Riemann problem is reduced to determining the classical solution of a free boundary problem of the Euler equations in ℜ1(δ) as follows:

On the free boundaryx=x(t), we have the generalized Rankine-Hugoniot conditions (2.10),which are now reduced t o

while on the other boundaryx=g(t), we have that

We draw the following conclusion about this problem:

Lemma 5.2 If the initial data satisfies thatρ0,1＞0 andu0=u1,then the free boundary problem(5.5),(5.6),(5.7)admits a unique classical solution in ℜ1(δ)for sufficiently smallδ ＞0.

Proof The Euler equations (5.5) can be rewritten in the characteristic form [19, p.6]

Based on this lemma, we immediately have the following conclusion about the singular Riemann problem (1.1), (1.2), (1.6):

Lemma 5.3 Under the SS condition, the singular Riemann problem (1.1), (1.2), (1.6)admits a unique local piecewise smooth solution foru0≤ur.

Consider the caseur ＜u0＜～ur, with ～urdetermined by (5.12) and (5.19).We seek a smooth solution in an angular domain surrounded by a delta shock and a forward shock wave.In this case, the polytropic gas is compressed by the delta shock on the left, and there may be a forward shock locally in front of the delta shock.We proceed to find this kind of solution.

First of all,by the Rankine-Hugoniot condition,it is easy to get the shock solutionx=s′(0)twith left state being (～ρ1,u0), ～ρ1＞ρrand right state being (ρr,ur) at the original point, by solving

Define an angular domain

where bothx=x(t) andx=s(t) are unknown curves to be determined.Then we formulate a free boundary problem in ℜ2(δ) with equations (5.5) in it, and the boundary conditions (5.6)onx=x(t), while we have the following boundary condition onx=s(t):

Here [u] =ur-u(s(t)-,t), and so on.Also, the Lax entropy conditionρ(s(t)-,t)＞ρris required on the shockx=s(t).

In summary,by searching for the forward shock,we have assumed the following conditions:

Here ～ρ1is determined uniquely by the first equation of (5.12).Under these assumptions, the second condition of (5.14) can be rewritten as

which is attainable by the intermediate value theorem.When the equality (5.19) holds, the minimal characterizing number of matrixH2satisfies that|H2|min= 1.Thus, ifu0＜～ur, we have that

Therefore,it follows by[19,Theorem 3.1.1 and Theorem 3.5.1]that we have the existence of a uniqueC1solution to the free boundary problem (5.5), (5.6), (5.14) on ℜ2(δ) for sufficiently smallδ ＞0.Thus, we have

Lemma 5.4 If the initial data satisfiesur ＜u0＜～ur, with ～urdetermined by (5.12) and(5.19), then the free boundary problem (5.5), (5.6), (5.14) admits a unique classical solution inℜ2(δ) for sufficiently smallδ ＞0.

Based on this lemma, we immediately have the following conclusion about the singular Riemann problem:

Lemma 5.5 Under the SS condition, the singular Riemann problem (1.1), (1.2), (1.6)admits a unique local piecewise smooth solution forur ＜u0＜～ur.

Combining Lemmas 2.7, 5.1, 5.3 and 5.5, we arrive at

Theorem 5.6 Under the SS condition, the singular Riemann problem (1.1), (1.2), (1.6)admits a unique local piecewise smooth solution foru0＜～ur.More precisely, this solution consists of a delta shock followed by a forward rarefaction wave ifu0≤ur, and by a forward shock wave if ～ur ＞u0＞ur.

In the above discussions, the SS condition requires thatul ≥u0, i.e.the pressureless gas flows into the delta shock.Otherwise, whenul ＜u0, we add a contact discontinuityx=ulton the left of the delta shock, with the state between these two waves being a vacuum.Then, we obtain the unique local piecewise smooth solution for any initial data by the following corollary:

Corollary 5.7 Under the SS condition, the singular Riemann problem (1.1), (1.2), (1.6)withρl=0 admits a unique local piecewise smooth solution foru0＜～ur.Moreover,the solution consists of a delta shock followed by a forward rarefaction wave ifu0≤ur, and by a forward shock wave if ～ur ＞u0＞ur.

5.2 Application to the Piston Problem

In this subsection, we consider a free piston problem.More precisely, letting thex-axis be a tube with constant cross sections,there is a piston with massm0＞0 moving in the tube that separates the tube into two parts.There is a pressureless gas in the left part and a polytropic gas in the right.Without loss of generality, we suggest that the thickness of the piston is zero,so it reduces to a point mass.Att= 0, assume that the piston lies atx= 0, and that the states of gas on both sides are uniform, namely, (ρl,ul) and (ρr,ur), respectively, withρl,r ≥0 as well asul,rbeing constants.

For the pressureless flow, we assume that the particles on the left side will stick to the piston once they collide.Meanwhile, the polytropic gas satisfies the slip boundary condition on the right surface of the piston.A special interesting case is where there is no gas on the left side of the piston; things are then reduced to a free piston problem with the free piston taking a positive mass and velocity moving between the polytropic gas and the vacuum.

Both of the equations characterizing the pressureless flow on the left hand side of the piston and the polytropic gas on the right hand side of it are compressible isentropic Euler systems given by (1.1), where the state equation of the former isp=0 and that of the latter isp=ργ.Assume that the trajectory of the piston isx=y(t) withy(0) = 0.Then we have a typical problem of fluid-solid coupling.For the pressureless flow on the left of the piston, we have the free boundary problem

Note that the term on the right hand side of the second equation in (5.21) represents the force acting on the particles sticking on the piston.This forcewp(t) is due to the reacting forces resulting from the change in the momentum of those particles hitting and then sticking to the piston, according to Newton’s Third Law.Obviously, this only acts on the particles that stick to the surface of the piston.Meanwhile,ωρ(t) represents the total mass of particles that stick to the piston from 0 to timet.

For the polytropic flow on the right hand side of the piston, the free boundary problem is formulated as

The fourth line is an impermeability condition established on the free boundary.

Moreover, the motion of the piston satisfies Newton’s Second Law,

where the subscript “+” denotes the right limit state near the piston, and “-” denotes the left one in the sequel.

Determining the solution of the piston problem is reduced to solving the coupled problems(5.21)-(5.23).By the theorem of momentum, we can get the force enacted by the piston from(5.21) as follows:

Comparing (5.25) and (5.27), the same equation for the trajectory of a piston and a delta shock front means that solving the piston problem (5.21)-(5.23) is equivalent to solving the singular Riemann problem, just by regarding the delta shock as a free piston.

We conclude the main results of this section as follows:

Theorem 5.8 The singular Riemann problem of one-dimensional isentropic compressible Euler equations with discontinuous flux(1.1),(1.2),(1.6)is equivalent to the free piston problem characterized by(5.21),(5.22)and(5.23)in the sense that the weight of the delta shockωρ(t)is exactly the mass of the piston at timet, and the function of the delta shockx=x(t)is nothing but the trajectory of the piston, provided that the same boundary conditions are proposed on the delta shock and the piston.

Then it follows from Theorem 5.6 that we have the following conclusion about the existence of the piston problem:

Theorem 5.9 The free piston problem (5.21)-(5.23) admits a unique local piecewise smooth solution ifu0＜～ur.More precisely, this solution consists of a forward rarefaction wave in front of the piston whenu0≤ur, and a shock wave when ～ur ＞u0＞ur.

Furthermore,by the analysis regarding the singular Riemann problem,we also can conclude some properties of the movement of the piston for different initial data.For example, iful ≤u0≤ur,there is a vacuum state on the left side of the piston.If,in addition,u0＞the piston moves with a reduced acceleration until the density of the gas on its right hand side decreases to zero.

Remark 5.10 For the singular solutions constructed in Section 4, similar results can be derived so long as we consider the properties of the piston, such as whether it can release or absorb gases on either side.More precisely, we have the following two cases:

Case 1 The left surface of the piston can release, if the gas leaves it, or absorb, if the gas runs to it, pressureless gas that keeps the flow near it uniform, while the right surface can release, if the gas leaves it, or absorb, if the gas runs to it, a polytropic gas that keeps the flow near it uniform.

Case 2 The piston absorbs all of the particles that run to it, but it never releases any gas on either side.This corresponds to the over-compressing condition on the piston.

For any given timet ＞0, during the time [0,t], we assume that the mass concentrated on the left and right surface of the piston are, respectively,

The positiveml,r(t) means the absorption of the piston from the left or right side, and the negative one means the release.By the theorem of momentum,

where we have chosen thex-axis direction as the positive direction of velocity.This, together with (5.28), gives that

which is equivalent to (2.14) as well.

6 Discussion

So far, we have finished the construction of solutions to the singular Riemann problem for isentropic compressible Euler equations with discontinuous flux (1.1), (1.2), (1.6), which consists of a delta shock, a rarefaction wave, a shock wave, a contact discontinuity and a vacuum.Note that, whenρ0= 0, we refer to (1.6) as the classical Riemann initial data, but there are still differences here.The classical Riemann problem corresponds to the shock tube experiment, where the interface between two initial states will disappear.In this paper, this interface will always exist, and it has some special properties, such as releasing or absorbing gases on either side.Under the over-compressing condition (1.5), the solution may still be nonunique, due to the multiplicity of intermediate states between waves.It is necessary to propose a suitable condition on the discontinuity of the flux to get the unique solution.Fortunately,the combination of a slip boundary condition for a polytropic gas and an adhesion condition for a pressureless gas works well, and we can get a unique local piecewise smooth solution of a free piston problem under this condition by showing the equivalence of the singular Riemann problem and the piston problem.This indicates that by proposing different suitable conditions on the discontinuity of the flux, one may get solutions corresponding to different physical problems.

As was shown in Section 5 above, we obtained the local existence of piecewise smooth solutions with clear geometrical structure to a free piston problem, under the sufficient but not necessary condition thatu0＜～ur.Whenu0≥～ur,some other theories or methods are necessary to obtain corresponding solutions that might contain more abundant wave structures.We will,in future,conduct work regarding the global existence of the solutions we constructed in Section 5.

Conflict of InterestThe authors declare no conflict of interest.