改进A*算法在喷浆机器人路径规划中的研究

苏 畅,袁 泉,李子强,余晓帆

(安徽理工大学 机械工程学院,安徽 淮南 232001)

基于目前国家智慧矿山建设的背景,喷浆机器人的研发与应用获得了较大的进步。作为一种电子、机械、人工智能等多学科交叉融合的复杂系统,自主行走能力是喷浆机器人在矿井环境应用中的重要性能标准[1]。由于井下巷道复杂的环境情况,喷浆机器人需要具备自主运动能力,以及对巷道环境的感知和路径规划能力,以高效、可靠的完成喷浆作业。其中,路径规划是非常关键的,为了保障了机器人可以顺利的抵达目标点[2],需要机器人在未知环境中规划出一条从起点到目标点的平稳路径,常见的路径规划算法包括Dijkstra算法[3]、A*算法[4]、D*算法[5]、D*Lite算法[6]。其中,D*和D*Lite算法多用于不确定的动态环境,而在已知的静态环境下,Dijkstra和A*算法可以更快速地找到最优路径。Dijkstra算法是以搜索点与起点之间的代价为基础来搜索最短路径,但由于其搜索范围太大,使得搜索效率低下。A*算法是在Dijkstra算法的基础上添加启发函数的路径搜索算法,并综合考虑了搜索点与起点以及搜索点与目标点两种代价,这样可以平衡路径代价和搜索时间。但是在实际的喷浆机器人路径规划中,A*算法存在安全性低,转折路径多,平滑性较差等问题。

针对以上问题,目前学者们已经提出了许多改进A*算法。王中玉等[7]通过调整计算方法与函数比例来减少路径搜索时间和多余节点数目。辛煜等[8]在经典A*算法的基础上,将可搜索邻域数目从八个扩展到了无限个,并且可以在任何方向进行搜索,既减少了求解的路径长度,又极大的降低了拐点的数量。赵以毛等[9]重新设计启发式函数,减少了机器人路径规划的时间,且规划的路径更加平滑。吴飞龙等[10]对传统评价函数作出改进,同时设置了安全阈值并对路径节点进行优化。陈靖辉等[11]采用定向搜索的方法去除了对称搜索路径,由此减少了经过的节点数量。ZHANG等[12]首先通过经典A*算法规划出一条从起点到目标点的安全路径,再利用关键点选择方法进行二次规划,将路径中多余的中间节点删除,只保存起点、拐点和目标点,从而减少了搜索节点的数目和规划时间。陈若男等[13]利用领域矩阵方法对障碍物进行搜索,虽然改进了路径的安全性,但是路径的搜索效率并没有得到提高。本文在以上研究的基础上,对A*算法的评价函数,子节点的选取方式,以及路径平滑等方面进行改进,使改进算法在路径规划中具有快速,高效,更平滑,安全性更强的特点。

1 A*算法

1.1 环境建模

环境建模指的是在进行路径规划之前,喷浆机器人通过视觉或激光传感器将真实的物理环境转变成计算机能够识别的抽象环境。W.E.Howden在1968年提出了栅格法[14],因为这种方法在计算障碍物信息时较为简单,而且容易实现,因此被普遍地用于路径规划的环境建模上。通过栅格法把环境空间分割成若干个栅格单元,每个栅格的尺寸都是一样的,并对其进行定义来表达障碍物的信息。栅格单元的尺寸对路径规划的精度和效率有很大影响,当栅格分割的较小时,栅格个数较多,搜索空间过大,导致路径规划耗时长,效率低下。当栅格分割的较大时,环境空间划分的不够细致,导致路径规划的准确性下降,但栅格数量少可以缩短路径规划时间,提高效率。因此,需要确定大小合适的栅格地图,通常根据实际环境中障碍物的稀疏程度和路径规划的要求来确定。图1是一个20*20的栅格地图,白色栅格为空闲区域,能够让喷浆机器人自由通行,黑色栅格为障碍区域,机器人无法通行。

图1 20×20栅格地图

1.2 经典A*算法

A*算法具有搜索效率高、规划速度快等特点,已经广泛应用于路径规划。A*算法首先在起点开始寻找附近节点,然后根据评价函数选择移动代价最少的点作为下一个搜索节点,直至扩大到目标点。A*算法的评价函数f(n)的表达式为:

f(n)=g(n)+h(n)

(1)

式(1)中,g(n)为起点到当前节点的移动代价,h(n)为当前节点到目标节点的估计代价,也称启发函数。

若h(n)的评估值远小于g(n),则f(n)将近似等于g(n),此时A*算法的遍历节点会增多,搜索效率将大大降低;若h(n)远大于g(n),此时A*算法路径规划的速度变快,但会出现穿过障碍物的情况。因此启发函数h(n)决定了A*算法的搜索效率。欧几里德距离、曼哈顿距离和对角线距离是常用h(n)的预测方法。相比于曼哈顿和对角线距离,欧几里德距离具有更高的计算精度,而且更容易搜索最优路径,因此本文选取欧几里德距离对h(n)进行移动代价预估。假设起点坐标为(s1,s2),目标点坐标为(g1,g2),则欧几里德的启发函数为:

(2)

2 改进A*算法

2.1 评价函数的优化

在A*算法的介绍中提出,A*算法的核心是f(n),其中g(n)的值是固定的,因此对启发函数的优化通常是围绕h(n)实现的。针对实际的工作需求,h(n)越贴近实际的路径代价,其节点的选择准确度就越高,但h(n)的复杂程度越高,搜索节点就会越多,导致路径规划的运算速度降低,所以选择合适的h(n)是十分重要的。评价函数是移动代价与估计代价的和,通过更改移动代价与估计代价的权重,可以控制A*算法更偏向移动代价或是估计代价,如果移动代价的权重过大,则路径规划的速度较慢但可以搜寻到最佳路径;如果估计代价的权重过大,则路径规划的速度快但无法保证搜寻到最佳路径。因此本文更改评价函数的公式为:

f(n)=g(n)+(1+r/R)*h(n)

(3)

式(3)中,r为当前点到目标点的长度,R为起点到目标点的长度。即在估计代价h(n)前更改系数,从而改变估计代价的权重,以提高算法搜索路径的速度。

2.2 优化子节点的选择方式

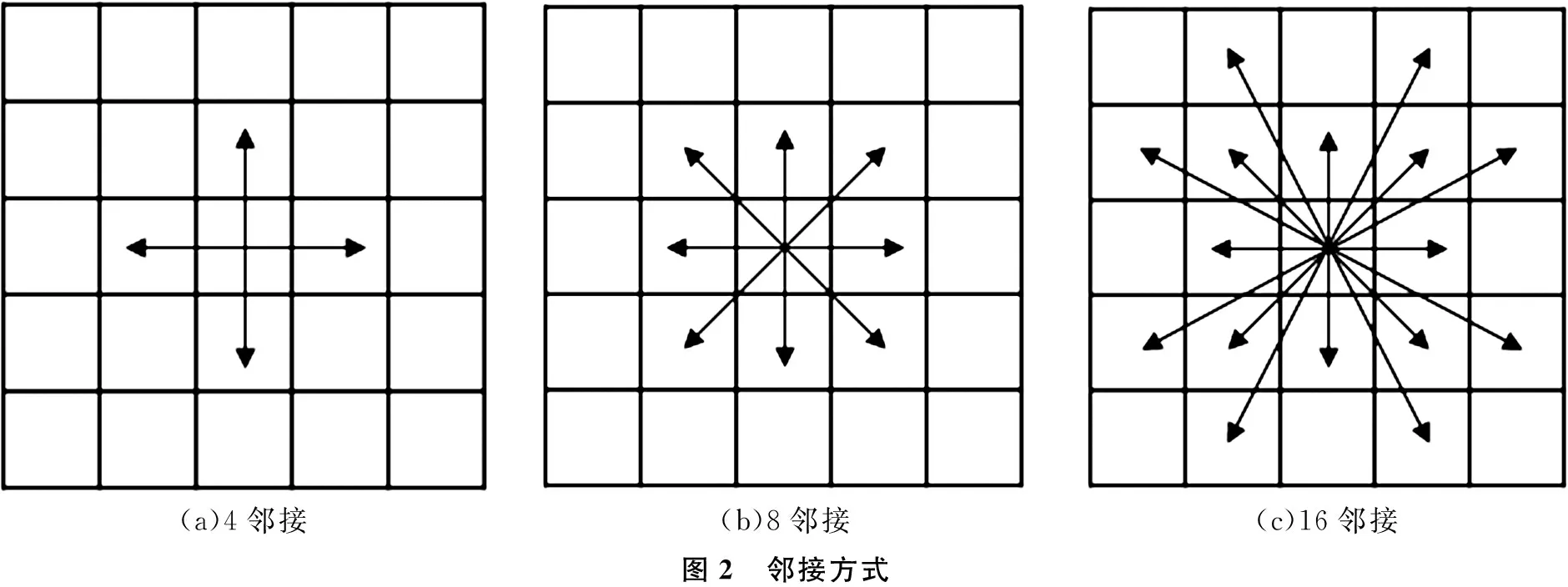
A*算法在寻找从起始点到终点的路径过程中,有4邻接和8邻接两种常用的选择子节点的方式,如图2(a)、图2(b)所示,但这两种方式规划的路径拐点较多且路径长。为此本文选择16邻接的方式,如图2(c)所示,该方式规划的路径拐点少、路径短,适合喷浆机器人的路径规划。

自费疫苗并不是某些网友所说的试验性的，都是正式销售的，而且基本是进口疫苗（有些是国产的），这些进口疫苗是美国FDA认证过的，在欧美日等发达国家是免费的计划内疫苗，所谓的自费只是需要家长来付这笔费用。

A*算法在生成其子节点后,对子节点进行判断,如果子节点存在障碍物,则不生成该位置的子节点,而是选取评价函数值最小的子节点作为路径节点,因此,所规划出的路径会穿过图3(a)所示障碍物的顶点,或与图3(b)所示的障碍物距离太近而发生碰撞,从而导致路径规划失败,甚至造成机器人损坏。图3中,三角形是机器人路径规划的起点,圆形是目标点,黑色线段是规划的路径。

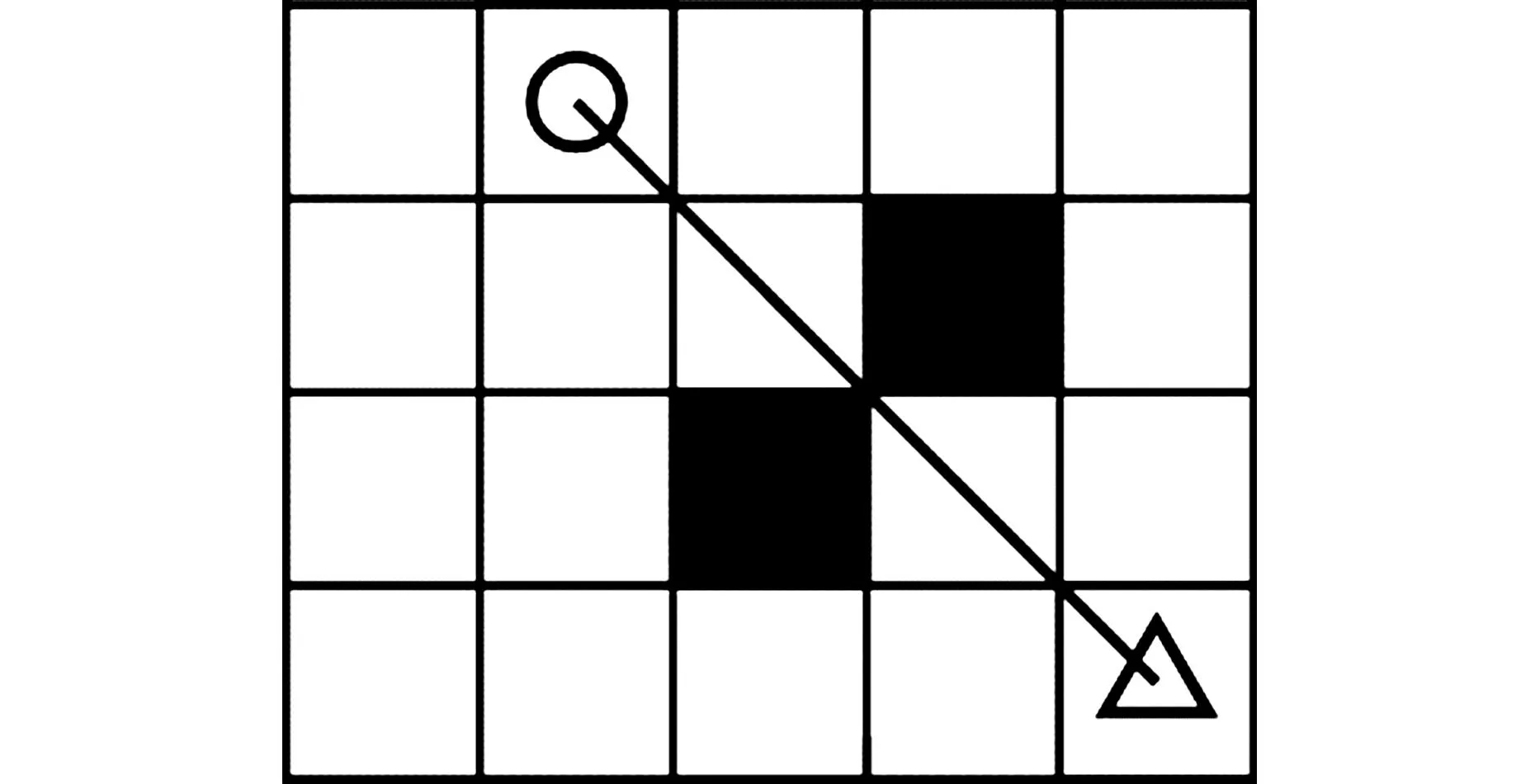
(a)

为了改善经典A*算法安全性低的问题,改进子节点的选择方式,在父节点生成子节点的时候,对子节点与障碍物之间的位置关系进行判断,改变子节点的选择方式,防止机器人在移动过程中出现斜穿障碍物顶点的问题,有效地避免了机器人与障碍物之间的碰撞,提高了喷浆机器人移动过程中的安全性。图4所示为16个子节点的分布图,本文设计的子节点选择方式为:

图4 子节点分布图

(1)若子节点1或5为障碍物,那么子节点2、4、6、8、9、10、13、14均不作为预选节点;

(2)若子节点3或7为障碍物,那么子节点2、4、6、8、11、12、15、16均不作为预选节点;

(3)若子节点无障碍物则不作处理。

通过优化子节点的选择方式,改进的A*算法规划的路径不会斜穿障碍物或离障碍物距离过近,如图5(a)、图5(b)所示,有效的避免了碰撞,机器人路径规划的安全性得到提高。

(a)

2.3 路径平滑度优化

经典A*算法在规划路径时,由于路径节点位于栅格中心,导致规划的路径具有多个拐点、平滑性差等问题。在喷浆机器人实际的作业环境中,上述问题对其工作效率会产生较大影响。为了解决这些问题,本文对路径进行了平滑度优化,以减小路径转折的角度。本文选择贝塞尔曲线法对路径进行平滑处理。贝塞尔曲线是一种应用于二维图像的曲线,它的取点方式是在两条线段上寻找一个可以将两条线段等分的点,再在其连线上寻找到一个可以等比例平分这条连线的点,这个点就是贝塞尔曲线上的一点,贝塞尔曲线上的其他点则通过改变比例得到,这些点组成的曲线就是贝塞尔曲线。二阶贝塞尔曲线公式如式(4)所示。

B(t)=(1-t)2P0+2t(1-t)P1+

t2P2,t∈(0,1)

(4)

式(4)中,P0是起点坐标,P1是目标点坐标,P2是位置点坐标。

贝塞尔曲线拟合的方法是:在一个平面上选择3个不同线的点A、B、C,将三个点依次连成一条直线,在线段AB和BC上分别选择点D和E,使AD/AB=BE/BC,连接DE,并在DE上确定一点F,使得DF/DE=AD/AB=BE/BC,如图6所示,让选取的点D在第一条线段上从点A移动到点B,然后确定所有点F,并将点F移动的轨迹连接起来,所得到的曲线就是贝塞尔曲线。

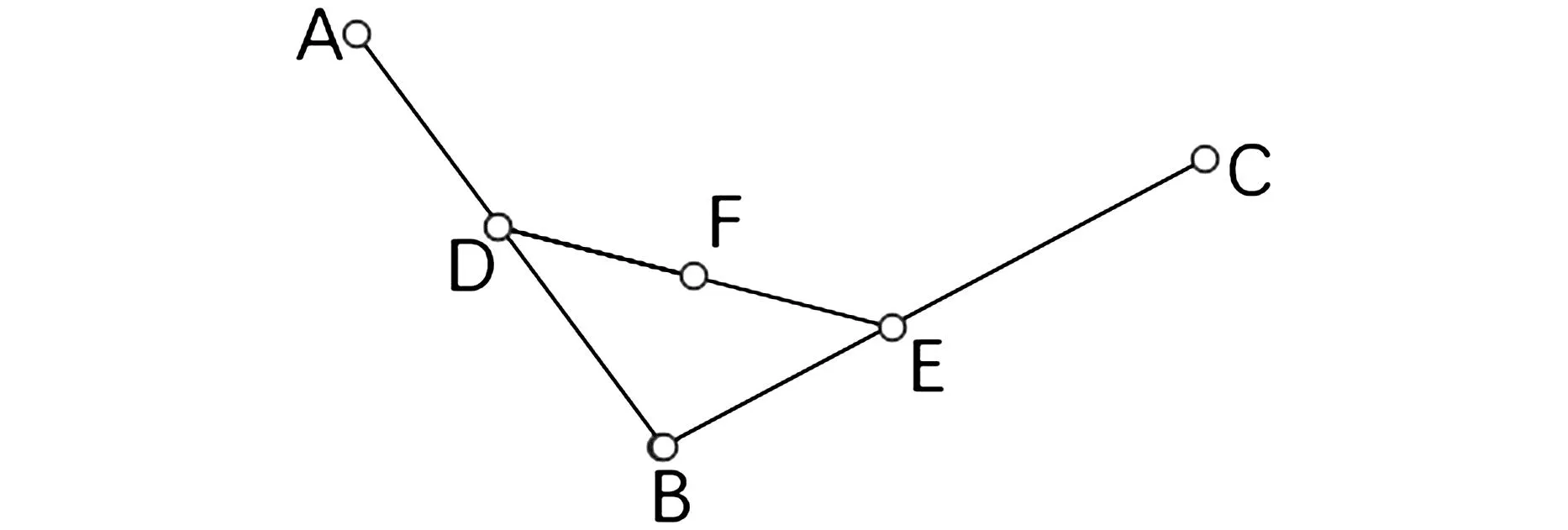
图6 原理图

3 实验与分析

3.1 仿真实验

在喷浆机器人工作过程中,煤矿环境中存在着大小不一的施工材料和障碍物。为了对本文提出的改进A*算法的有效性进行验证,使用经典A*算法与本文所提的改进A*算法在不同大小的栅格地图上展开仿真试验。实验环境为CPU Inter Core i7 12700F,内存16GB,实验工具MATLAB 2019a。本文首先在尺寸20×20的栅格地图上展开实验,每个栅格是边长为1个单位的正方形,栅格地图障碍物按照20%的比例随机生成,其中不同形状的黑色栅格表示煤矿环境中不同大小的施工材料和障碍物。传统A*算法与本文改进A*算法的路径规划的实验结果如图7所示,图中三角形是路径规划的起点,圆形是路径规划的的目标点。图7(a)中实线是经典A*算法规划的路径,图7(b)中黑色实线是改进A*算法平滑后的路径。经过比较可以看出,在相同环境下,与经典A*算法规划的路径相比,改进A*算法规划的路径转折角度小,安全性高,路径更加平滑。

(a)经典A*算法

仿真实验在3种不同尺寸但障碍率都为20%的栅格地图上分别成功运行10次(实验中存在障碍物堵住机器人前进路径的情况),记录传统A*算法和改进A*算法运行时路径搜索时间和路径长度。不同尺寸地图的起点和目标点不同。

地图尺寸为20×20时,起点坐标为(6,4),目标点坐标为(18,19)。

地图尺寸为50×50时,起点坐标为(3,40),目标点坐标为(46,10)。

地图尺寸为100×100时,起点坐标为(20,80),目标点坐标为(90,20)。

仿真结果见表1。

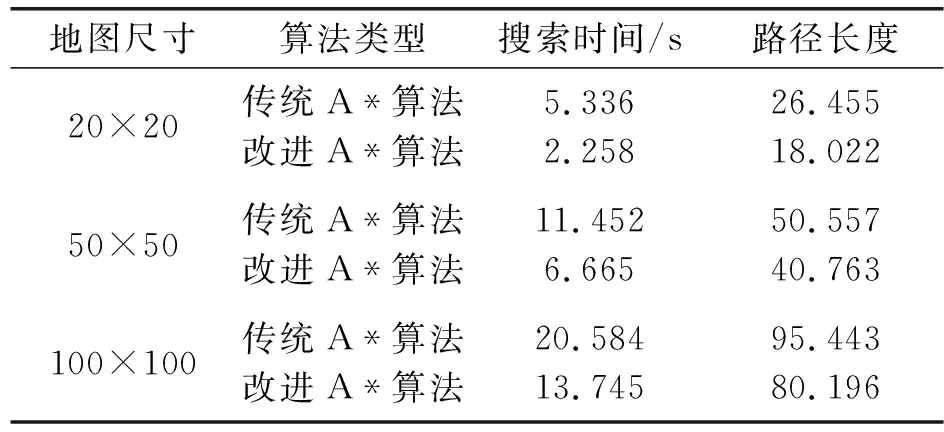
表1 路径规划参数对比表

表1给出了在不同大小的栅格地图上,经典A*算法相对于改进A*算法路径规划的时间和规划路径的长度。从表1中能够发现,与经典A*算法相比,改进A*算法的寻路时间节省了50%左右,路径长度节省了20%左右,这说明改进A*算法路径规划的效率更高、路径更短。

3.2 结果分析

经过多次仿真实验得出的结果,分析得出路径优化的三个主要因素。

(1)评价函数的优化。通过更改估计代价的权重,以减少路径规划过程中搜索节点的数量,减少了搜索时间,增加路径规划的效率。

(2)优化子节点的选择方式。通过改变子节点的邻接方式,降低了路径的拐点,使得路径更短,同时优化子节点的选择方式,通过增加喷浆机器人与障碍物之间的距离,从而避免危险情况发生。

(3)路径平滑。选择贝塞尔曲线对路径进行平滑处理,减少了路径的转折角度,保证了喷浆机器人运动时的平稳性。

通过以上实验和分析可知,喷浆机器人采用改进A*算法进行路径规划,可以提高工作效率,保证安全性和平稳性,具有一定的应用价值。

结语

为了解决经典A*算法在路径规划时存在的缺陷,本文对A*算法的评价函数、子节点的选择方式以及路径平滑作出了一定的优化。改进A*算法通过改变估计代价的权重来减少搜索路径的时间,提高路径规划的效率;然后为了使喷浆机器人不会斜穿障碍物顶点,对子节点的选择方式进行改进,增加了机器人与障碍物之间的安全距离,改善了机器人运动过程中的安全性;最后对路径进行平滑优化,减少路径的拐点,规划出更平稳的路径。经过实验分析,本文改进的A*算法搜索时间少、路径短、安全性高、路径更加平滑,证明了所提改进算法的优越性,可用于煤矿环境中的喷浆机器人路径规划。