干式空心并联电抗器绕组匝间绝缘故障特征分析
2024-03-22李增悦咸日常张海杰赵飞龙李嘉洋
李增悦, 咸日常, 张海杰, 咸 峰, 赵飞龙, 李嘉洋, 王 玮
(1. 山东理工大学 电气与电子工程学院,山东 淄博 255000;2. 国网山东省电力公司超高压公司,山东 济南 250118;3. 山东七星电气科技发展有限公司,山东 淄博 255000)
0 引 言
随着电力系统容量增大,输电线路长度和电压等级不断提高,越来越多的并联电抗器接入电网中用以进行无功补偿。干式空心并联电抗器作为超高压变电站重要的无功补偿设备,因其具有无油、无铁心、结构简单、造价低、运维成本低等优点得到广泛应用[1-3]。近年来电抗器运行中的事故率呈现明显增长趋势,绝缘损毁、着火事故时有发生,严重威胁着电网的安全运行。对电抗器的诸多事故进行分析,发现匝间绝缘故障占很大比例,充分暴露出干式空心并联电抗器的纵差和过流保护失效[4-7]、有效监测及保护技术手段不完善等问题。电抗器绕组匝间绝缘采用的是环氧浇注工艺,绝缘包封受潮、散热不良、制造工艺缺陷、断路器投切所产生的过电压等都会对其绕组匝间绝缘产生影响[8-14],同时匝间绝缘故障发展迅速,易导致电抗器起火[15],因此对干式空心并联电抗器绕组匝间绝缘故障进行监测具有重要意义。
对于干式空心并联电抗器的运行状态监测及故障诊断,目前已有不少的研究和方法。红外成像仪测温只能对电抗器的最外层包封进行测温,而内层包封温度的变化却不能获得[16],不能及时诊断由内部包封故障引起的温度升高。当电抗器的漏磁通受到周围环境影响时,通过感应线圈感知感应电压的变化来检测故障是否发生[17]的检测精度降低。利用高频脉冲振荡法进行干式空心并联电抗器的匝间绝缘试验在技术上是可行的,但是此方法需要在电抗器停电条件下进行[18-19],绕组绝缘故障诊断的时效性差。因干式空心并联电抗器有别于串联电抗器,其容量大、绕组层数多,通过检测各支路电流变化来判断电抗器绕组是否发生匝间绝缘故障的成本高且安装测量装置复杂[20-21]。因此,亟须寻找某个适应于干式空心并联电抗器绕组匝间绝缘状态在线监测的敏感状态量。相较于过程繁琐的解析计算法和成本高且具有一定危险性的试验测量法,更多学者倾向于使用有较强后处理功能、能够直观呈现运行结果的有限元分析软件来实现对电抗器不同运行状态的分析[22]。文献[23]以一台干式空心实验电抗器的最外层包封为例,得到不同匝间短路位置对应的电动力幅值和相位的关系,但并未对不同层、不同匝间短路位置下的故障绕组受力变化情况进行分析。文献[24]对干式空心电抗器稳态时的磁场、电动力及电场进行了分析,但并未涉及匝间绝缘故障。文献[25]分析了干式空心电抗器不同位置匝间短路的电感、总电流、层电流及磁场变化情况,但分析的电磁特征量较少。
为此,本文在有限元软件中对干式空心并联电抗器进行建模,将仿真得到的电抗器正常运行时各层自感、各层电流值与解析计算值进行对比,以验证模型的可靠性。通过研究电抗器绕组不同位置匝间绝缘发生故障时各物理量的变化情况,获取用于绕组匝间绝缘故障监测的状态量,为实现干式空心并联电抗器绕组匝间绝缘状态的在线监测与故障诊断提供相关技术思路。
1 解析计算原理
1.1 电抗器等效电路
干式空心并联电抗器由多层绕组并联而成,每层绕组可以看作一条支路,每条支路由其对应绕组的等效电阻和等效电感串联组成。在低频下,电抗器各层绕组之间的等值电容可忽略不计[26],若电抗器共有n层绕组,则电抗器正常运行情况下的等效电路如图1所示。
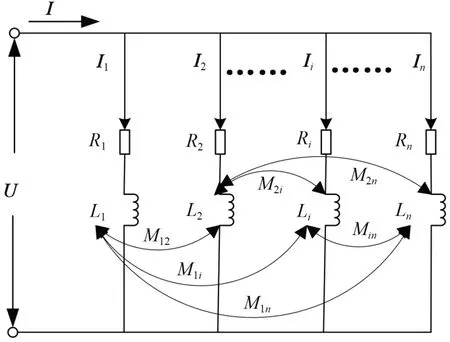
图1 正常运行情况下电抗器等效电路Fig.1 Reactor equivalent circuit under normal operation
根据图1可得电抗器正常运行时满足的电压电流方程,如式(1)所示。
式(1)中:i=1,2,…,n;U为施加在电抗器两端的电压;Ii为电抗器第i层支路电流;Ik为电抗器第k层支路电流;Ri、Li为第i层支路的电阻、自感;Mik为第i层与第k层绕组之间的互感;j为虚数单位;ω为角频率。
若某层绕组匝间绝缘出现故障导致匝间绝缘失效,如图2 所示,则该绕组结构发生变化,形成短路环。根据电磁感应原理,短路环中也会出现感应电流,短路环阻抗很小,因此会感应出很大的电流,从而对电抗器的运行状态产生影响。对应等效电路中多了一条短路环支路,等效电路及对应方程如图3和式(2)所示。
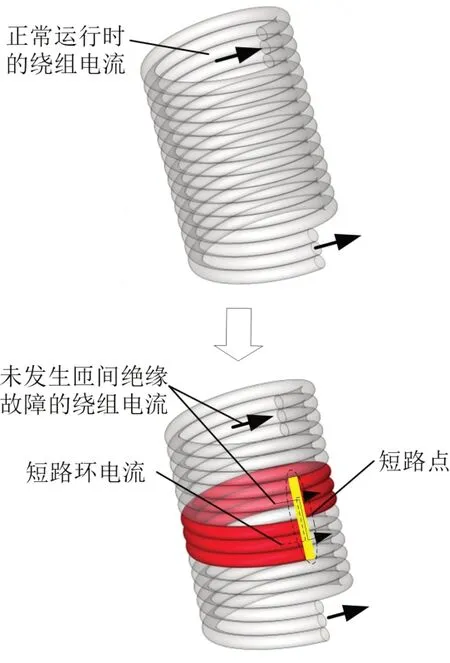
图2 正常运行与匝间绝缘故障时的绕组电流示意图Fig.2 Schematic diagram of winding current under normal operation and interturn insulation fault

图3 匝间绝缘故障情况下电抗器等效电路Fig.3 Equivalent circuit of reactor in case of interturn insulation fault
式(2)中:In+1为短路环电流;Rn+1、Ln+1为短路环的电阻、自感;Mkn+1为短路环与各层绕组之间的互感,其余参数含义同式(1)。
1.2 绕组电感计算
将电抗器每层绕组等效为一个薄壁螺线管,绕组之间互感的计算等效为两个同轴螺线管间互感的计算[27],如图4 所示。将两线圈间互感公式进行坐标变化并在两个绕组高度上进行积分,可得电抗器第i、j层绕组之间的互感,如式(3)所示。
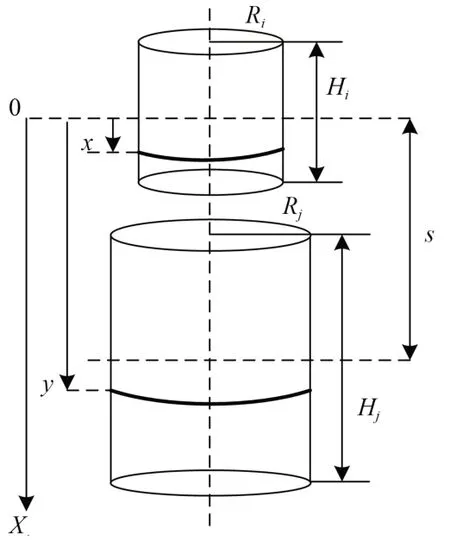
图4 绕组电感计算示意图Fig.4 Schematic diagram of winding inductance calculation
式(3)中:Mij为电抗器第i、j层绕组之间的互感;µ0为真空中的磁导率;Ri、Rj为电抗器第i、j层绕组的半径;ni、nj为电抗器第i、j层绕组单位高度的匝数;Hi、Hj为电抗器第i、j层绕组的高度;s为两绕组的中心距,计算绕组电感时取为0。电抗器绕组的层自感即为i=j的情况。
将根据式(3)求得的电感参数代入电抗器的电压电流方程中,在给定频率的电压下,求解对应方程可得各支路电流。
2 干式空心并联电抗器仿真模型
2.1 模型建立与验证
本文的研究对象为一台适用于35 kV 电压等级的干式空心并联电抗器,该电抗器的主要技术参数见表1。在有限元软件中建立该电抗器的“场-路”耦合二维几何模型,如图5所示。
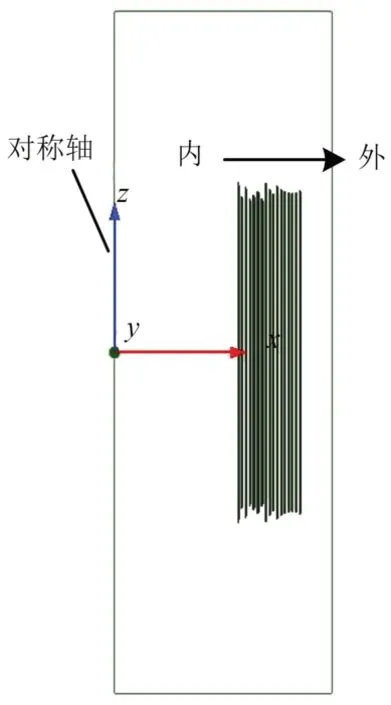
图5 电抗器二维几何模型Fig.5 Two-dimensional geometric model of reactor
在电抗器两端施加额定电压,将稳定运行时的各层绕组自感、电流的仿真值与解析计算值进行比较,如图6 所示。从图6 可以看出,各层绕组自感、电流仿真值与解析计算值的误差均不超过5%,在研究允许的范围内,由此验证了仿真模型的可靠性,满足后续进行绕组匝间绝缘故障状态设置与分析的精度要求。
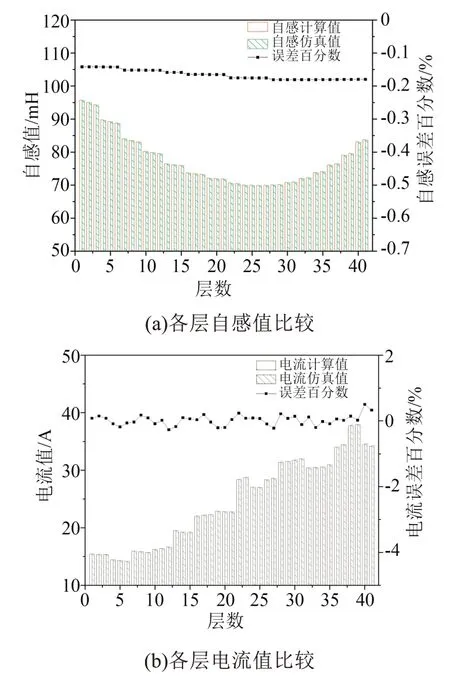
图6 各层绕组自感、电流的仿真值与解析计算值比较Fig.6 Comparison on simulation values and analytical calculation values of self-inductance and current of windings in each layer
2.2 绕组匝间绝缘故障设置
该电抗器共有41层绕组,沿径向方向由内向外分别记为第1~41 层,取第1、11、21、31、41 层为绕组匝间绝缘故障的设置层,分别记为c1、c11、c21、c31、c41,故障层在绕组中的位置如图7(a)所示。因为电抗器绕组部分轴向对称,所以只在其上半部分设置匝间绝缘故障,记绕组高度为H,在所选故障层的H/2、5H/8、3H/4、7H/8 和H高度处设置匝间绝缘故障点,分别标号为1、2、3、4、5,如图7(b)所示。文中研究的是电抗器在承受某一电压作用下绕组匝间绝缘故障时各状态量的最大值相对于在此电压作用下电抗器正常运行时对应状态量最大值的变化率,故电抗器在正常运行与绕组匝间绝缘故障时其两端所加电压相同。为了能够及时识别匝间绝缘故障,文中主要研究单匝匝间绝缘失效形成单匝匝间短路这种绕组的初期绝缘故障情况。
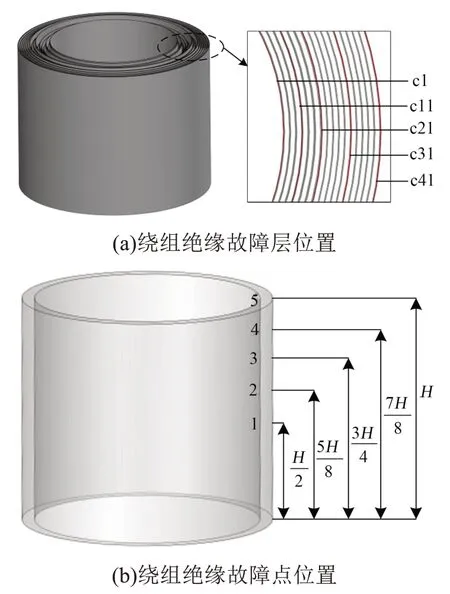
图7 绕组匝间绝缘故障设置示意图Fig.7 Schematic diagram of winding interturn insulation fault setting
3 绕组匝间绝缘故障的电气特征量分析
3.1 电气特征量计算原理
因干式空心并联电抗器的层数多,对绕组的各层进行监测较为困难,所以文中主要研究电抗器主回路的电气特征参数变化。将电抗器对外整体等效为电阻和电抗的串联结构,根据其两端所加电压与得到的回路总电流,计算可得等效电阻、等效电抗、等效阻抗、功率因数角、功率因数及有功功率损耗,计算式如式(4)~(6)所示。
式(4)~(6)中:Z为电抗器的等效阻抗;U、I为电抗器所加电压、回路总电流;R、X分别为电抗器的等效电阻、等效电抗;θ为电抗器的功率因数角;φ为电抗器的功率因数;p为电抗器的有功功率损耗。
3.2 电气特征量变化率分析
根据式(4)~(6)可得在绕组不同位置出现单匝匝间短路故障时各电气特征量的变化率,如图8所示。从图8 可以看出,电抗器绕组单匝匝间短路后,回路总电流、等效电阻、功率因数和有功功率损耗呈现正变化率,而等效电抗、等效阻抗和功率因数角呈现负变化率。各电气特征量变化率随故障位置变化在径向上由内层向外层逐渐增大,在最外层有所减小。在轴向上,各电气特征量变化率随故障位置变化由绕组中部至端部逐渐减小。等效电阻、功率因数和有功功率损耗的变化率范围分别为505.30%~4 720.71%、506.63%~4 921.16%、507.95%~5 129.94%,变化率均在500%以上,能有效反映电抗器绕组匝间绝缘故障。而回路总电流、等效电抗、等效阻抗和功率因数角的变化率均在10%以内,变化率相对较小,在c1 端部位置发生单匝匝间短路故障时的变化率甚至接近于0,不能有效反映电抗器绕组匝间绝缘故障。

图8 随单匝匝间短路位置变化的电抗器各电气特征量变化率Fig.8 The change rate of each electric characteristic quantity of the reactor with the short circuit position between single turns
由于施加在电抗器两端的电压不变,绕组单匝匝间短路后电抗器的等效阻抗减小,故回路总电流增大。等效阻抗的变化范围并不大,虽其电阻部分有很大变化,但电抗器阻抗以感抗为主,且远大于等效电阻,单匝匝间短路对电抗的影响小,故电抗器的等效阻抗和功率因数角变化小。等效电阻增大,等效阻抗减小,由此反映的是功率因数变化率较大。绕组单匝匝间短路后,故障层未发生匝间绝缘故障的绕组电流及其他层电流有所变化,但这些层电流变化引起的有功功率损耗变化小。虽然短路环电阻很小,但短路环电流激增,可高达正常运行电流的数百倍。图9为短路环电流相对于短路环所在层正常运行时电流的变化率。由图9 可知,短路环电流的变化率均在25 000%以上,匝间短路后短路环电流变化非常大,根据有功功率损耗值与电流的平方成正比,故有功功率损耗的变化很大。图9 印证了图8(g)中有功功率损耗的变化率很大的结果。
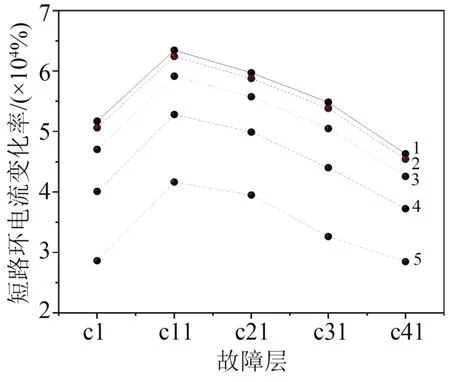
图9 短路环电流变化率Fig.9 Short-circuit loop current change rate
4 绕组匝间绝缘故障的磁感应强度、受力分析
4.1 磁感应强度、受力计算原理
根据毕奥-沙伐定律可得单匝载流线圈在空间点产生的磁感应强度,在绕组轴向高度上积分,可得单层载流绕组在空间点所产生的磁感应强度,如图10所示。由此可得第i层绕组在空间点所产生的轴向、径向磁感应强度,如式(7)所示。
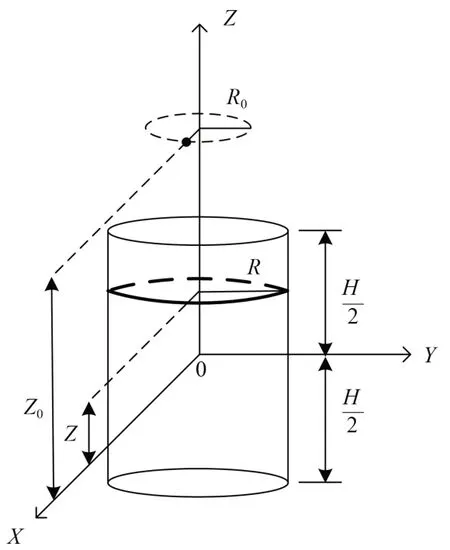
图10 单层载流绕组磁感应强度计算示意图Fig.10 Schematic diagram for calculating magnetic induction intensity of single-layer current-carrying winding
式(7)中:BZi、BRi分别为电抗器第i层绕组在空间点产生的轴向、径向磁感应强度;µ0为真空中的磁导率;n为绕组单位高度的匝数;I为绕组电流;R、R0分别为绕组、空间点的半径;H为绕组高度;Z0为空间点的高度;Z为绕组高度的积分量。
将所有绕组在该点处产生的磁感应强度相加,得到该点处的轴向、径向磁感应强度如式(8)、式(9)所示。
式(8)~(9)中:BZ为空间点轴向磁感应强度;BR为空间点径向磁感应强度;N为电抗器绕组总层数。
电流密度为J的绕组截面受力如式(10)所示。
4.2 磁感应强度、受力变化率分析
电抗器正常运行与c1 中部位置单匝匝间短路情况下空间磁感应强度出现最大值时的空间磁感应强度分布如图11所示。
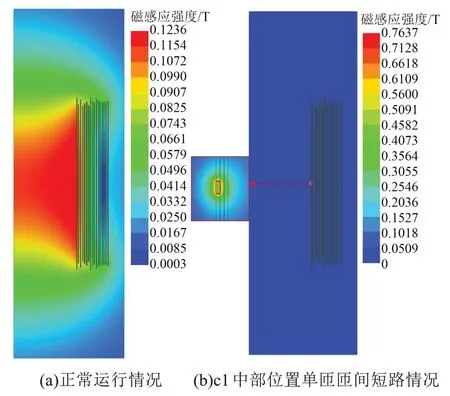
图11 正常运行与匝间绝缘故障时的空间磁感应强度分布Fig.11 Spatial magnetic induction intensity distribution under normal operation and interturn insulation fault
由图11(a)可知,电抗器正常运行时的空间磁感应强度呈轴向对称分布。由图11(b)可知,绕组匝间短路后,短路环中感应出的大电流会使周围磁场产生畸变,且磁感应强度最大值出现在短路环附近。由磁场对电流回路作用的安培力公式可知,绝缘故障绕组的受力也会发生变化,可能会导致电抗器绕组变形。随单匝匝间短路位置变化的空间磁感应强度、故障绕组受力变化率如图12所示。
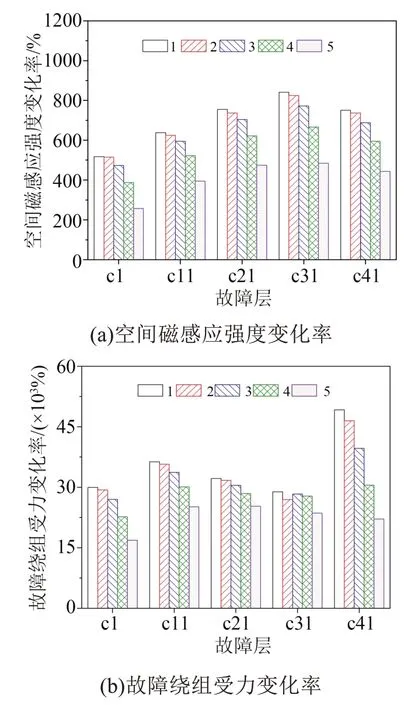
图12 随单匝匝间短路位置变化的空间磁感应强度、故障绕组受力变化率Fig.12 Spatial magnetic induction intensity and force change rate of fault winding varying with the position of single interturn short circuit
从图12(a)可以看出,空间磁感应强度变化率随故障位置变化从绕组中部向端部逐渐减小,变化率均高于200%。由式(10)可知,绕组受力由绕组中电流及周围磁场决定,受两方面因素影响,变化复杂,从图12(b)可以看出,故障绕组受力值总体变化率很大,均高于15 000%。两者均能灵敏地反映绕组匝间绝缘故障。
5 干式空心并联电抗器绕组匝间绝缘故障敏感状态量分析
综上对干式空心并联电抗器绕组匝间绝缘故障的电气特征量、磁场和绕组受力变化的分析,对各物理参量进行比较,结果如表2 所示。由表2 可知,非电气特征量的空间磁感应强度和故障绕组受力值均对绕组匝间绝缘故障反应敏感,但磁感应强度的测量易受周围环境因素的干扰,而绕组受力值变化率虽最为显著,但受力测量实施成本高、难度大,不宜作为绕组匝间绝缘故障的监测量。电气特征量中功率因数、等效电阻和有功功率损耗不仅变化明显,且易于监测。可通过电抗器回路上的电压、电流互感器获得电流、电压信号的幅值和相位信息,经过计算获取这3个参数信息,作为电抗器匝间绝缘故障的在线监测量。
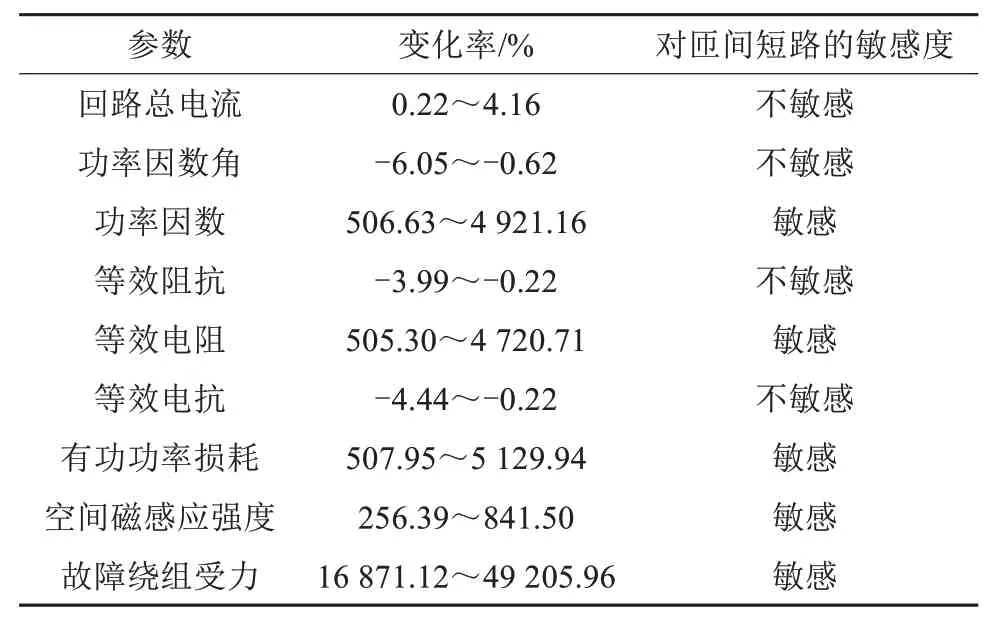
表2 干式空心并联电抗器绕组匝间绝缘故障物理量对比Tab.2 Comparison on physical quantities of interturn insulation fault of dry-type air-core shunt reactor winding
6 结 论
基于现阶段干式空心并联电抗器绕组匝间绝缘故障监测的有效手段不足,本文通过有限元分析软件对干式空心并联电抗器进行建模仿真分析,研究了在其绕组单匝匝间短路绝缘故障情况下的电、磁、力变化规律,得到以下结论:
(1)干式空心并联电抗器绕组单匝匝间短路后,短路环电流升高至正常运行电流的数百倍,有功功率损耗增加,温度异常升高,危及电抗器绕组绝缘,而电抗器回路的总电流变化很小,不易监测诊断。
(2)干式空心并联电抗器的回路总电流、等效电阻、等效电抗、等效阻抗、功率因数角、功率因数和有功功率损耗的变化率随绕组单匝匝间短路位置的变化趋势为:在轴向上,由中心向端部逐渐减小;在径向上,整体由内层向外层逐渐增大,在最外层有所减小。
(3)干式空心并联电抗器功率因数、等效电阻、有功功率损耗以及空间磁感应强度、故障绕组受力值在绕组单匝匝间短路后均明显增加,可选用功率因数、等效电阻、有功功率损耗等电气特征量作为其匝间绝缘故障的在线监测量。
