高压直流电场非接触测量传感器的设计与研究
2024-03-22杨琦张春丽吴锦涛李婵
杨琦,张春丽,吴锦涛,李婵
(1.云南电网有限责任公司临沧供电局,云南 临沧 677000;2.云南电力技术有限责任公司,云南 昆明 650011;3.云南电网有限责任公司昆明供电局,云南 昆明 650011)
0 前言
高压直流输电技术以其自身的优势,在电网建设和发展中发挥了重要作用。为保证高压直流带电设备的安全稳定运行,有必要对带电设备进行定期检修和维护[1-3]。在设备检修过程中,电气工人应避免触电事故的发生,有必要提前测量带电设备周围空间的直流电场,确定电场是否超过安全阈值,电力操作人员的位置是否安全,以确保电力工人的生命安全[4]。目前,国内外直流电场测量方法主要有接触式和非接触式两种[5-7]。鉴于本文所测试的对象是一个电压等级为的高压直流带电器件±500 kV和±800 kV。另外,本文选择了高压直流电场强度的非接触测量。目前直流电场测量的传感原理主要包括电容器、MEMS技术和光学三种[8]。考虑到现有技术和实验条件,本文选择了一种基于可变面积的电容传感器,即旋转电容传感器。该传感器的优点是输出信号稳定、成本低、功耗要求高。为了保证传感器的工作时间,本文选用了低功率无刷直流电机[9]。目前,旋转电容传感器的体积还比较大,它不适用于可穿戴式电场测量设备。一般采用固定装置或手持式旋转电容传感器来实现对高压直流电场的测量。提出了一种低功耗、量程可调、灵敏度可调的新型旋转电容传感器。该传感器通过与终端智能预警APP平台连接,可以实时测量环境的直流电场强度。具有直流输电运行场景的安全预警功能。
1 直流电场传感器的测量原理
本文采用旋转电容传感器测量高压直流充电设备周围的电场。详细推导了直流电场测量原理。设计传感器的结构,分析了传感器电路的等效原理。
1.1 传感器电场测量原理
旋转电容传感器利用高压直流充电装置在周围空间产生的感应电荷来测量空间中的电场强度[10]。因为直流电场是一个准静态电场,我们可以从高斯定理中知道公式(1)。
其中,E是空间直流电场强度;S是电场传感器的有效电荷感应面积;∑qi是传感器表面累积的自由电荷的代数和;ε0是真空介电常数。
旋转电容传感器驱动屏蔽电极通过电机旋转。屏蔽电极与电机轴共用地。所述感测电极在直流电场作用下的有效感测面积随时间呈周期性变化。为了保持与地面相同的电位,当感应电极暴露于空间电场时,感应电极上会积聚一定量的感应电荷[11]。旋转电容传感器的工作原理如图1所示。
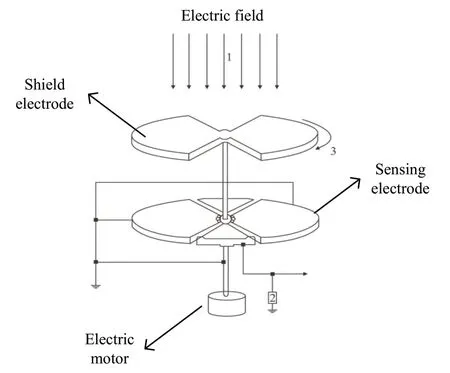
图1 现场研磨传感器工作原理
屏蔽电极使传感电极保持“曝光-屏蔽”三种状态。为了方便它们,传感电极和屏蔽电极叶片都采用扇形结构[12-13]。根据扇形面积公式,推导出传感电极的有效传感面积随时间变化的表达式。
其中,T是诱导区变化期;ω是电机旋转角速度;R是屏蔽电极和感应电极叶片的开口波瓣数;r是风扇叶片的内径,也是风扇叶片的外径。
感测电极上的感生电荷Q(t)由屏蔽电极调制以产生周期性变化的感生电流信号i(t)。i(t)的表达式如式(3)所示。
将公式(2)代入式(3),传感器电极上感应电流信号i(t)的表达式如公式(4)所示。
其中,E是被测空间的直流电场强度;n是屏蔽电极和感应电极叶片的开口波瓣数。
当传感电极完全暴露在电场中时,有效传感面积最大,感应电流值最大[14]。当传感电极被屏蔽电极完全屏蔽时,有效传感面积最小,感应电流值最小。
1.2 传感器等效电路原理
旋转电场传感器是基于电容器传感原理的(如图2)。通过周期性改变传感电极上的有效传感面积,实现对高压直流电场环境中相应直流电压信号的调制,周期性地改变感应电荷[15]。旋转电场传感器的固有电容值随时间变化,公式(5)。

图2 旋转电场传感器的等效原理
其中,CS(t)是传感器的固有电容;S(t)是感应电极的有效感应面积d是屏蔽电极和传感电极之间的垂直距离;ε是介电常数。
根据旋转电场传感器的结构特点和直流电场测量原理,将传感器结构等效为如图3所示的电路模型。
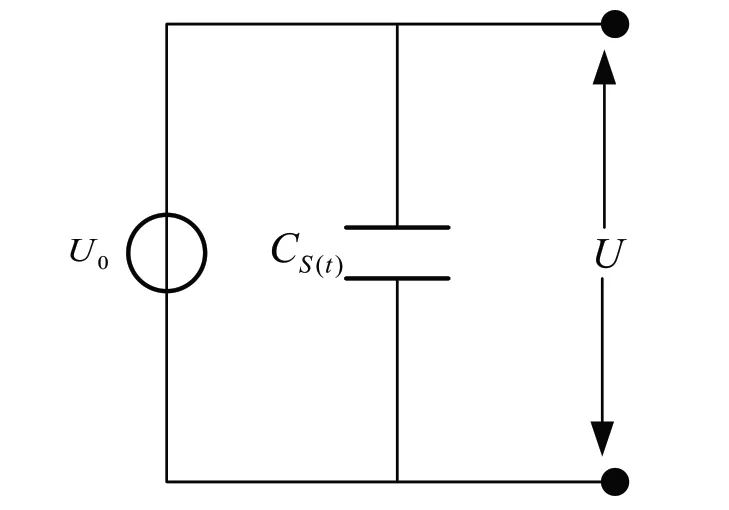
图3 旋转电场传感器电路图
图3中U0是被测直流充电装置的工作电压,电压幅值恒定,且随时间变化不变化。CS(t)是传感器的固有电容。U是由旋转电场传感器输出的可测量直流电压信号。
根据式(3),信号处理电路将交流感应电流信号转换为可测量直流电压信号之间的放大系数,可以确定输出电压信号与测量电场E之间的关系式。本文将电场传感器置于标准直流均匀电场中进行标定试验。确定了输出电压信号与实测直流电场E的关系。如果传感器的性能参数满足要求,可以用电场传感器测量高压直流电场。
2 传感单元优化设计
由式(4)可知,传感器电极上感应电流的大小不仅与传感器电极的有效感应面积、传感器电极扇形叶片的数量有关,感应电流的大小还受电机转速、直流电场强度、感应电极的距离和倾角的影响。
2.1 传感电极扇形叶片数
感应电极扇形叶片的数量与感应电流信号i(t)的大小呈线性关系。考虑到电场传感器的灵敏度,单位时间内扇形叶片数越大,感应电极的有效感应面积越大,感应电流的振幅越大,传感器的灵敏度就越高[16]。传感电极会受到边缘效应的影响。随着风机叶片数的增加,边缘效应的影响越来越明显。因此,需要对传感电极的风扇叶片数进行参数优化设计。
本文将电场传感器的屏蔽电极和传感电极之间的距离保持不变[17-18]。屏蔽电极和感应电极风扇叶片的外径和内径是固定的。电机角速度也保持不变。只考虑扇形叶片数对感应电流信号i(t)幅值的影响。
假设感应电流信号为临界最大值[19]。也就是说,当感测电极完全暴露于电场时,感测电极上的感生电荷量为q1。感应电极上的感应电荷量是当感应电极被完全屏蔽时产生的。感应电流信号的表达式,如式(6)所示。
其中,T为感测区域的变化周期。
利用COMSOL有限元仿真软件建立了感应电极扇形叶片数分别为2、4、6…16的电场传感器的仿真计算模型。传感器置于10 kV/m均匀直流电场环境中。将其放置在平行板电容器的上极板和下极板的中心。感应电流信号的计算振幅随扇形叶片的数量而变化如图4所示。

图4 风机叶片叶数对感应电流幅值的影响曲线
从图4可以看出,交流感应电流信号i(t)的幅值并不随感应电极风扇叶片数的增加而线性增加,当风扇叶片数=6时,交流感应电流的幅值最大,因为传感器的传感器电极受到边缘效应的限制影响传感器的测量结果。为了保证电场传感器的灵敏度性能,本文设计的电场传感器感应电极扇形叶片的波瓣数为6。
本文在传感器的实际设计中,采用屏蔽电极扇形叶片数=6,感应电极扇形叶片数=12,感应电极差动输出两路交流感应电流信号。每个感应电极的扇形开口波瓣数为6,可以抑制外部共模信号的干扰。
2.2 电机旋转角速度
根据公式(4),交流感应电流信号i(t)的振幅随电机旋转角速度线性增加。电机转动角速度与驱动频率的关系式(7)。
其中,f是电机驱动电压信号的频率。
可以看出,交流感应电流信号i(t)的振幅随电机驱动信号的频率线性增加[20]。研究了电机角速度对交流感应电流信号i(t)的影响。本文将其转化为对传感器性能参数的影响,重点是对传感器量程和灵敏度的影响。
从图5可以看出,随着电机旋转角速度的增大,传感电极单位时间的有效传感面积增大,感测电极上的感应电流信号幅值增大,电场传感器的输出直流电压信号幅值也增大,传感器的灵敏度系数也会增加,但范围会减小。
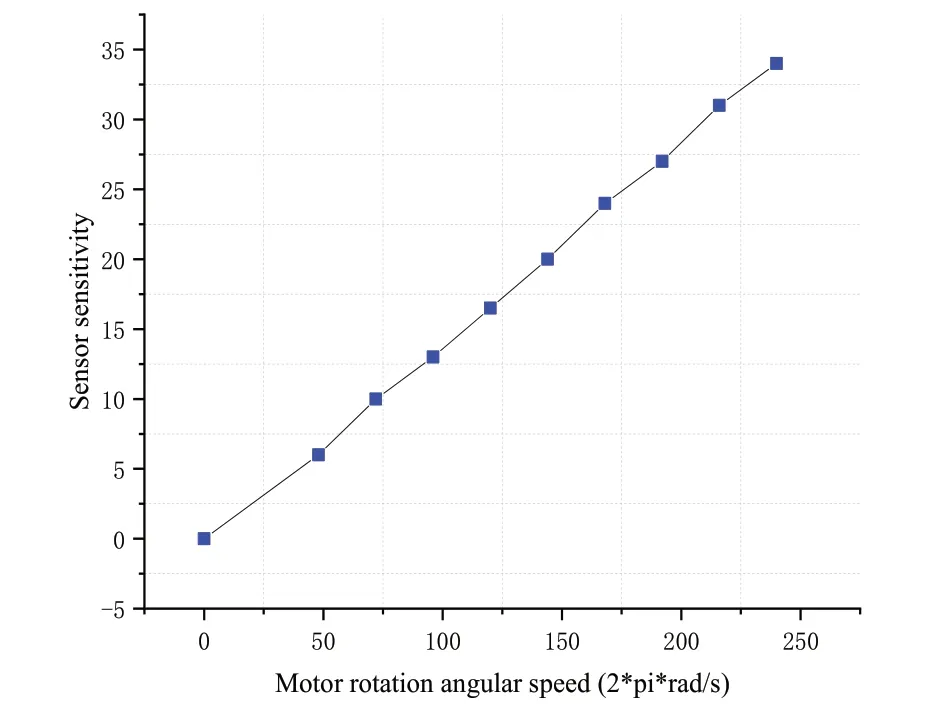
图5 电机旋转角速度对传感器灵敏度的影响
在电场传感器的设计过程中,考虑到传感器的功耗和实际使用寿命,选择电机驱动电压为3 V,电机驱动信号频率为240 Hz。
2.3 屏蔽电极和传感电极间距
感应电极上交流感应电流信号i(t)的大小与感应电极与屏蔽电极之间的距离和倾角有关。两者之间存在一定的倾角,使得传感电极与屏蔽电极之间的有效距离发生变化[21]。
由式(5)可知,传感电极与屏蔽电极之间的距离越小,传感器的固有电容越大。电极间距越大,边缘效应对传感器的影响越大。
考虑到边缘效应的约束和其他变量的影响,只有传感电极与屏蔽电极之间的距离和倾角不同,才会影响传感电极上的感应电荷量。确定屏蔽电极和传感电极之间的最佳有效距离。首先,保持屏蔽电极与传感电极平行,均匀缩小两电极之间的中心距离,计算不同距离下传感电极上感应电荷的大小。其次,保持屏蔽电极和传感电极之间的中心距离不变。屏蔽电极的倾斜角度从0到5均匀变化°。计算不同倾角下感应电极上感应电荷的大小[22]。
从图6可以看出,当屏蔽电极与传感电极之间的有效距离越小时,感应电极上的感应电荷Q(t)量越大,即交流感应电流信号i(t)幅值越大,传感器灵敏度越高。考虑到传感器的使用寿命和传感器对高压电场测量的精度,最终选择屏蔽电极与传感电极的间距为3 mm。
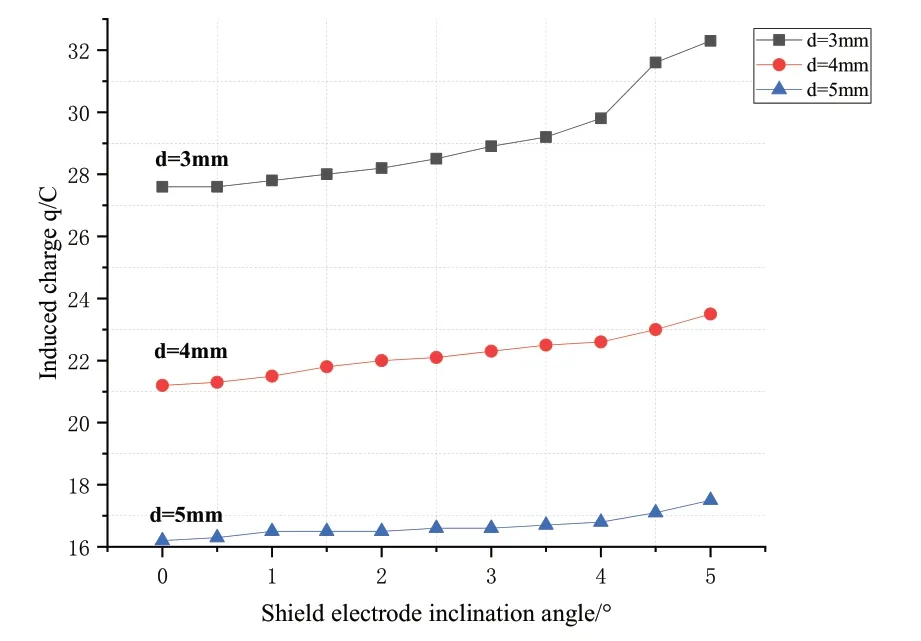
图6 两电极间有效距离对感应电荷的影响

图7 传感器单元处理的物理图像
保持屏蔽电极和传感电极之间的中心距离不变。当屏蔽电极倾斜角度较大时,屏蔽电极与传感电极之间的有效距离变小。感应电极上的感应电荷量Q(t)越大,交流感应电流信号i(t)的幅值越大,为避免电极间距较小时屏蔽电极与感应电极的碰撞,保持屏蔽电极和传感电极平行。
3 传感单元的物理处理与实现
为了便于电场传感器传感单元的结构设计和加工,传感器的屏蔽电极和传感电极叶片采用扇形开口方式。屏蔽电极和传感电极叶片的开口花瓣数、扇形内径、扇形外径和两电极上下间隙的实际加工参数如表1所示。

表1 传感单元结构的尺寸参数
屏蔽电极使用经处理过1 mm厚的铜片。屏蔽电极叶片开口波瓣数n=6,直流无刷电机金属轴接地。传感电极采用PCB工艺制作,工艺误差小±0.1 mm。感应电极叶片开口波瓣数n=12,采用12等分叶片结构。6个间隔扇区形成一个组,两个信号形成一个差分信号输出[23]。
旋转电场传感器感应将探头的屏蔽电极接地,感应电极采用差分信号输出结构,引线与信号处理电路板相连。电机控制电路和信号处理电路板安装在直流无刷电机下方,PCB电路板通过固定孔固定[24]。
4 高压直流电场传感器的标定
通过传感器标定实验,计算了直流电场传感器的静态指标。例如,范围、灵敏度、线性度和滞后误差等性能参数[25-26]。直流电场传感器的标定是准确测量传感器的前提。传感器校准原理如公式(8)所示。
其中E为两极板间均匀直流电场强度。U是两个极板之间的电位差。d是两个板块之间的距离。
校准装置基于平行板电容器。稳定的直流电压施加在电容器的上极板上,下极板接地,在上极板和下极板之间产生均匀的直流电场[27]。将直流电场传感器置于极板之间的均匀电场中,使其位于下极板的中心。通过公式E=U/d计算电场的大小。将其与电场传感器输出的电压幅值进行拟合,得到两者的标定曲线。
在图8所示的传感器标定实验中,上下极板之间的距离为10 cm,极板之间产生的均匀电场强度为0~100 kV/m。均匀调节高压直流电源的输出电压幅值,待传感器输出电压幅值稳定后记录实验数据。
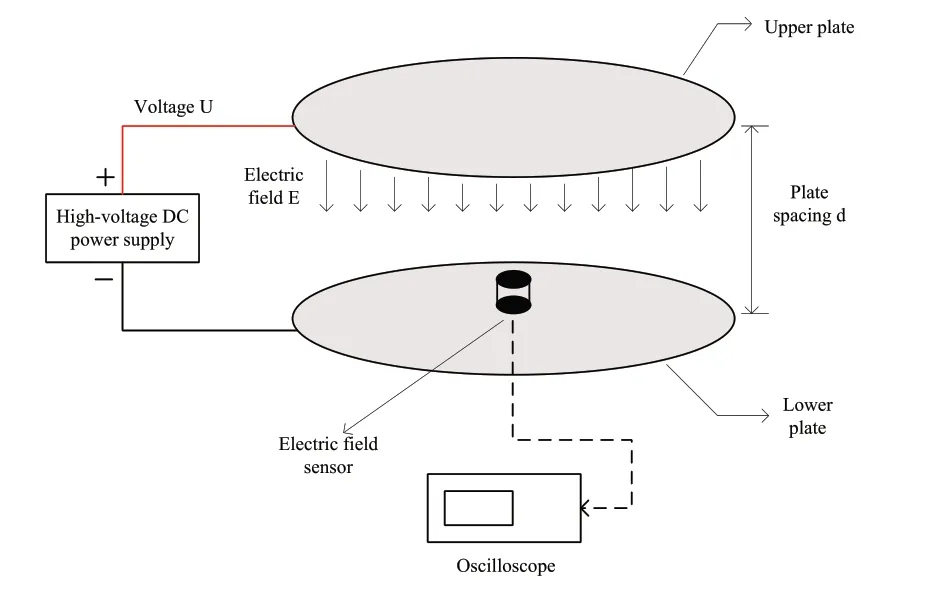
图8 电场传感器校准试验模型
根据表2中电场传感器的标定试验数据,我们可以画出电场传感器标定试验结果曲线,如图9所示。
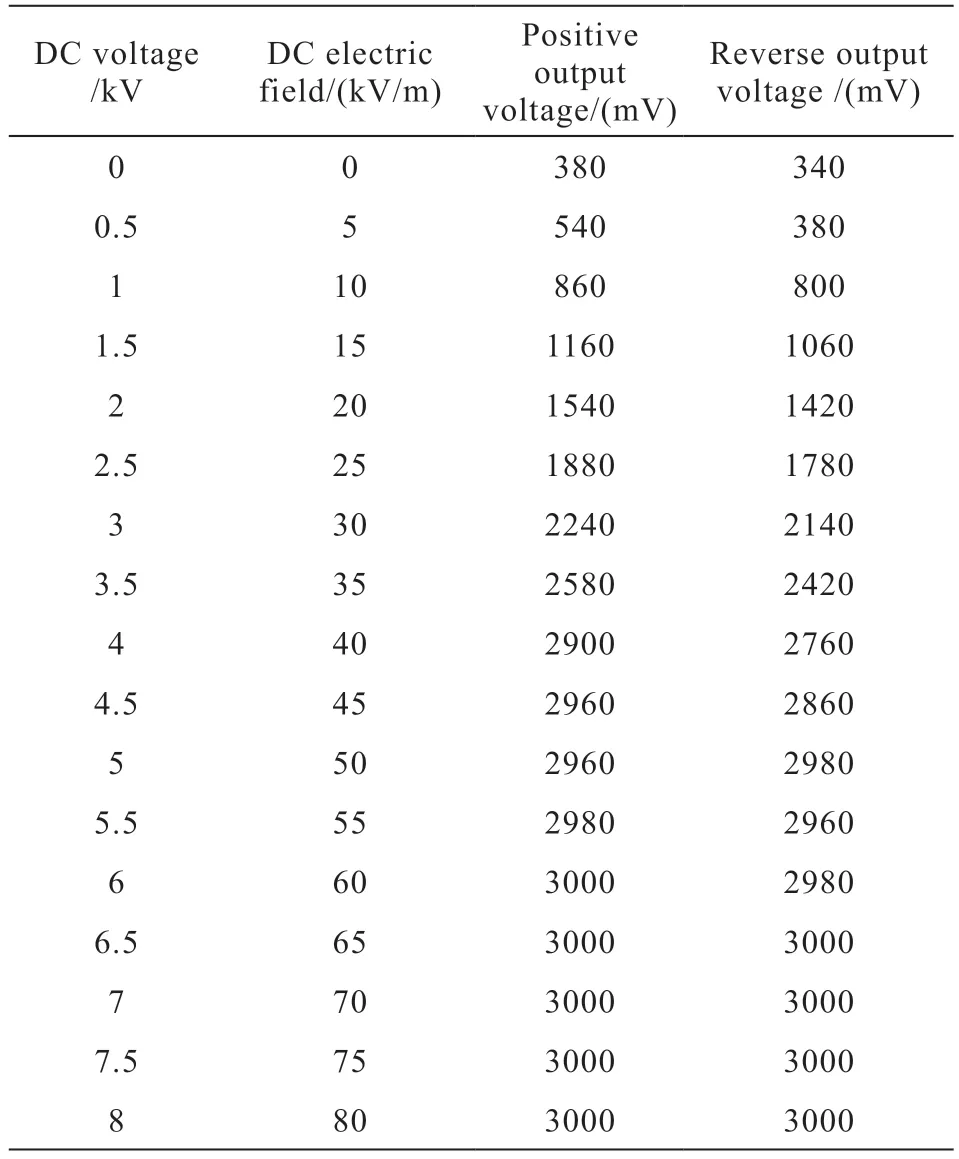
表2 电场传感器校准试验数据

图9 电场传感器校准试验结果曲线
由图9可知,当直流电场强度E=60 kV/m时,传感器输出电压幅值接近饱和,本文传感器在被测环境中,在给定直流电场强度的0~100 kV范围内,电场传感器测量值为0~65 kV。在给定的直流电场强度0~40 kV范围内,传感器输出电压信号幅值呈线性变化。根据该公式,传感器的迟滞系数计算为±5.3%,前后行程电场传感器测量值一致。
通过一组观测结果(E,U0)进行最小二乘线性拟合[28]。两者之间的线性关系如式(9)。
其中,K表示曲线的斜率值,该值反映了传感器的灵敏度。b表示传感器的体噪声。
从图10可以看出,曲线a是传感器的测量值曲线,曲线b是拟合直线,两条曲线在0~40 kV范围内线性关系相同。曲线b的计算斜率为K=65.6。根据定义,传感器灵敏度S=65.6。

图10 电场强度与传感器输出电压的拟合曲线
综上所述,静态指标包括传感器范围、分辨率、线性度和测量误差。通过表3中的传感器校准试验进行计算。

表3 电场传感器标定性能参数
由表3可知在0~±100 kV给定直流电场强度,传感器的量程为0~±65 kV,不满足0~±80 kV。当给定的直流电场强度大于40 kV时,传感器输出电压信号幅值不再随测量的直流电场强度线性变化。我们需要做进一步的实验来分析传感器性能参数缺失的原因。
5 结束语
本文基于高斯定理对传感器电场进行了测量。采用非接触法测量高压直流电场。该传感器的结构基于电容式传感器的原理,研制了一种自反馈低功耗直流电场传感器。传感器的量程和灵敏度可以实现动态反馈调节,这是本文的一个重要创新。
对直流电场传感单元结构参数的优化设计表明,传感电极扇形叶片开口的最佳波瓣数为n=6,屏蔽电极与传感电极的最佳距离为d=3 mm,可以知道传感器的范围是±65 kV/m,灵敏度系数为65.6,精度为0.5 kV/m,测量误差小于2%,传感器在测量范围内具有良好的一致性和可靠性±40千伏/米。随着直流电场测量范围的增大,传感器的线性度减小,测量误差增大±超过40 kV/m。
因此,本文提出的传感器仅适用于现阶段低量程电场强度的测量。为了提高传感器的性能参数,还需要进一步的研究和实验。使传感器的使用更加可靠,应用更加广泛。
