交直流配电系统储能优化配置方法
2024-03-22张鸿雁许长清皇甫霄文孙建行
张鸿雁,付 涵,许长清,罗 潘,皇甫霄文,孙建行
(1.国网河南省电力公司,郑州 450052;2.国网河南省电力公司经济技术研究院,郑州 450052;3.教育部智能电网重点实验室(天津大学),天津 300072)
随着全球对温室气体排放的日益关注,可再生能源大规模接入电网[1]。然而可再生能源固有的间歇性和随机性会造成电网实际运行成本、网络损耗、弃光和弃风率的增加[2-3]。储能系统ESS(energy storage system)在平抑新能源出力波动、缓解系统不确定性、改善负荷特性以及优化网络运行等方面发挥着重要作用,是实现可再生能源并网的关键技术[4-5],但相对较高的成本和较短的使用寿命,在一定程度上阻碍了储能系统的发展。因此,世界各地开展了从联合优化角度提高储能经济性和技术性的研究。文献[6]提出了一种以储能成本和提高负荷率奖励费用综合最优为目标的光储优化模型;文献[7]提出了一种考虑分时电价和最大暂态频率偏移的储能系统机会约束优化配置方案。现有研究表明,储能系统可获得潜在经济效益以降低投资成本并避免冗余配置。
另一方面,柔性直流技术和电力电子器件在提高新能源利用率方面也有巨大潜力[8]。交直流混合配电系统融合了交流配电系统和直流配电系统的优点,直流子系统可通过减少交直流转换过程中的能量损失来促进直流分布式电源的接入,交流子系统可通过电压源型换流器VSC(voltage source converter)调节系统电压、提供功率支撑。与传统的交流配电系统相比,交直流混合配电系统可以通过各个子系统之间的协调运行解决可再生能源并网所带来的问题[9]。此外,交直流混合微电网可合理调整交流、直流电源与负荷接入,能够有效减少电力转换装置的投资,因而得到广泛应用,文献[10]以日前调度的运行成本最小为目标,提出了一种含高渗透率可再生能源发电和电动汽车的交直流混合微电网的最优运行方案;文献[11]提出了一种基于经济调度的微电网储能优化配置方法。对于可再生能源渗透率较高的交直流混合配电系统,为平抑由可再生能源和电动汽车引入的波动,文献[12]不仅提出了一种能够有效提高系统经济性和灵活性的随机调度方法,还研究了储能与各种分布式能源的协调运行。现有文献表明,储能和交直流混合配电系统不仅能够提高系统的可控性,还能够提高可再生能源消纳能力,进而加快电力系统低碳转型。但现有研究忽略了储能无功调节能力和全寿命周期成本以及子系统之间的功率支撑能力。
本文面向交直流混合配电系统,综合考虑各子系统中储能与VSC的灵活配合,提出了一种储能容量双层优化模型。首先,建立了交直流混合配电系统相关模型;随后,建立储能双层容量优化配置模型,通过内外层迭代求解储能配置方案;最后,通过算例分析证明所提模型的有效性。
1 交直流混合配电系统建模分析
典型的交直流混合配电系统包括ESS、VSC、光伏PV(photovoltaic)、直流负荷和交流负荷,交流子系统和直流子系统通过VSC进行功率交互。
1.1 电池储能模型
电池储能系统BESS(battery energy storage system)主要由储存电量的电池本体和控制其充放电过程的换流器PCS(power conversion system)组成。PCS可以发出或吸收一部分无功功率以支撑电网电压稳定。储能系统的充放电功率需满足的约束为
式中:PESS,i(t) 和QESS,i(t) 分别为第i个储能系统在t时刻输出的有功和无功功率,本文设储能放电为正,充电为负;SESS,i为第i个PCS的接入容量;PESS.N,i和QESS.N,i分别为第i个储能系统输出有功和无功功率最大值。
当BESS接入直流配电系统时不考虑其无功特性,其充放电功率约束满足式(2)即可。此外,用荷电状态SOC(state of charge)表示储能的剩余容量,其值为储能剩余容量与储能总容量的比值。在运行过程中,电池储能系统需满足约束
式中:SOCi(t)为第i个储能系统在t时刻的荷电状态;Erate,i为第i个储能系统的额定容量;和分别为第i个储能系统的SOC 上、下限;SOCi(0)和SOCi(T)分别为第i个储能系统在运行优化周期内SOC的初始时刻和最终时刻的值。
1.2 换流站模型
交直流换流站是交直流混合配电系统中的核心设备。VSC能够独立控制有功和无功功率,可快速反转潮流并向交流系统输送无功功率,其运行功率约束为
式中:PVSC.ac,k(t)和QVSC.ac,k(t)分别为第k个VSC在t时刻传输的交流侧有功和无功功率;SVSC,k为第k个VSC的额定容量;PVSC.ac.N,k和QVSC.ac.N,k分别为第k个VSC传输的有功功率和无功功率最大值。
VSC 的有功功率损耗与其传输的有功功率和流过的电流有关,具体表示为
式中:PVSC.loss,k为第k个VSC 的有功功率损耗;η为VSC 的有功损耗系数,取值范围为3%~10%[13];PVSC.dc,k为第k个VSC输出的直流功率。
对于交直流混合配电系统而言,维持直流配电系统的有功功率平衡是系统安全稳定运行的关键,即直流配电系统输入的有功功率等于直流配电系统中的功率损耗与输出的有功功率之和。各VSC在保证直流配电系统功率平衡的基础下可独立控制其交流侧无功功率或母线电压。因此,需选择一个VSC 作为有功功率平衡换流器以保证直流配电系统功率平衡,其余VSC根据实际情况设定有功功率[14]。一般来说,VSC 间的协调控制可分为主从式控制和分布式下垂控制[15]。此外,交直流混合配电网中VSC 具有多种运行模式,包括PUac控制,PQ控制,UdcQ控制,UdcUac控制[16]。
1.3 交直流混合配电网Distflow 支路潮流模型
本文在传统交流潮流基础上,提出了适用于交直流混合配电系统的支路潮流模型。主换流器采用UdcQ控制,其他换流器采用PQ控制,交直流子系统约束如下。
(1)交流支路潮流约束为
式中:φi为以i为末节点的首节点集合;ϕi为以i为首节点的末节点集合;Ui(t)为t时段节点i的电压;Iij,ac(t)、Pij,ac(t)和Qij,ac(t)分别为t时段交流节点i流向交流节点j的电流、有功和无功功率;rij和xij分别为支路ij的电阻和电抗;Pi,ac(t)和Qi,ac(t)分别为t时段注入交流节点i的有功和无功功率之和,可表示为
式中:为t时段光伏电源注入节点i的有功功率;和分别为t时段储能注入节点i的有功和无功功率;PVSC.ac,i(t)和QVSC.ac,i(t)分别为t时段VSC 交流侧注入交流节点i的有功和无功功率,规定从直流配电系统流向交流配电系统为正;和分别为t时段节点i上负荷消耗的有功和无功功率。
(2)交流子系统运行电压水平约束为
式中,和分别为节点i的电压上、下限。
(3)交流子系统支路电流约束为
式中,为交流支路ij允许通过的电流最大值。
(4)直流支路潮流约束为
式中:Iij,dc(t)和Pij,dc(t)分别为t时段直流节点i流向直流节点j的电流和有功功率;Pi,dc(t)为t时段直流节点i上注入有功功率之和,可表示为
式中,PVSC.dc,i(t)为t时段VSC直流侧注入直流节点i的有功功率。
(5)直流子系统运行电压水平约束为
(6)直流子系统支路电流约束为
式中,为直流支路ij允许通过的电流最大值。
BESS 运行约束如式(1)~式(6),VSC 的运行约束为式(7)~式(11)。
2 双层容量优化配置模型
BESS 容量优化配置不仅要适应未来配电系统的安全性和可靠性,还要具有较好的经济性,以便推动BESS 的广泛应用。如图1 所示为本文所提出的储能双层容量优化模中,其外层优化模型负责解决BESS 容量规划问题;内层优化模型主要在外层优化模型给定的各BESS 的额定容量、额定功率和初始SOC的基础上解决系统的经济运行问题,并将得到的BESS 运行功率和套利收益、VSC 运行功率以及系统网损成本返回给外层优化模型;内外层模型交替求解得到最优配置方案。其中,外层优化模型采用遗传算法结合模拟退火算法求解,内层模型采用二阶锥规划求解。
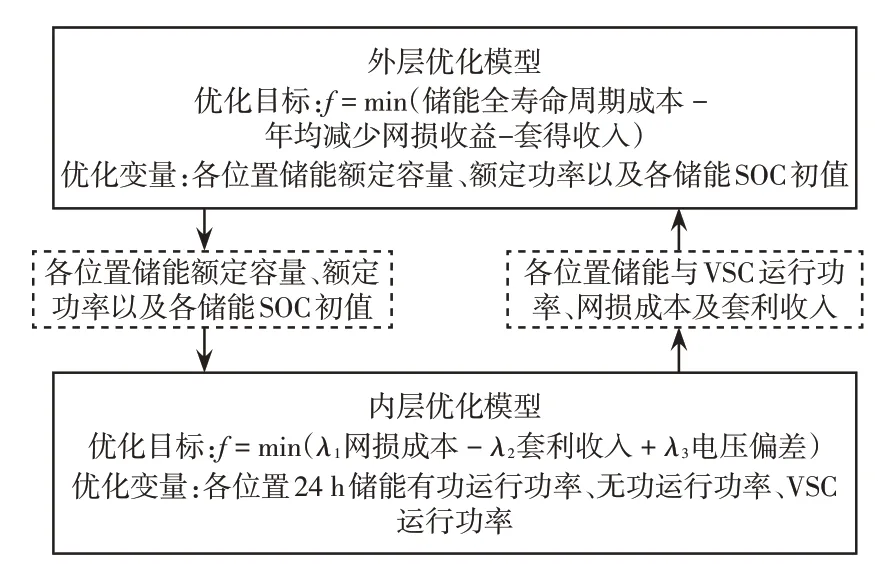
图1 BESS 双层容量优化配置模型Fig.1 Bi-level BESS capacity optimization model
2.1 内层优化模型
BESS 和VSC 协调运行可提高交直流混合配电系统的灵活性,平抑由可再生能源发电渗透率过高所导致的电压波动。本文中光伏电源按单位功率因数输出有功功率,BESS 的PCS 可以吸收或发出一定的无功功率用于无功补偿和电压支撑。当配电系统电压位于最佳运行区间时,该系统的安全性及经济性较好。通过储能系统和VSC 协调运行可以最大限度的将电压维持在最佳运行状态,模型的目标函数为
式中:CL为BESS 配置后配电系统的年均网损成本;CA为储能套利收益;ΔU为电压水平偏差;λ1、λ2和λ3为相应的权重系数;K、NESS、Ndc和Nac分别为VSC 的个数、ESS 的个数、直流子系统和交流子系统中的节点数;Ωi为节点i的相邻节点所构成的集合;price(t)为t时刻电价;BESS 在尽可能降损套利的基础上,应使电压接近或处于节点电压幅值的优化区间,即[Uthr,min,Uthr,max];G为一年中BESS运行天数。
内层优化模型是多时段最优潮流问题,本文采用Distflow支路潮流模型。求解储能规划模型的主要挑战是最优潮流问题的强非凸非线性,而凸化松弛处理可将非凸的非线性问题转化为二阶锥规划以进行高效求解。锥规划理论对数学模型具有严格限制,需对本文中存在决策变量乘积项和二次项的相应模型进行锥转换处理,具体分为以下3个步骤。
步骤1目标函数的线性变换。
用Iij,ac,2(t)、Iij,dc,2(t) 和Ui,2(t) 替换式(25)和式(27)中的二次项、和,将目标函数线性化为
由于式(25)中存在绝对值项|PVSC.ac,k(t) |,引入辅助变量pVSC,k(t)=|PVSC.ac,k(t) |,并增加约束
由于式(29)中存在绝对值项|Ui,2(t)-1 |,引入辅助变量μi(t)=|Ui,2(t)-1 |,并增加约束[18]
步骤2系统运行约束的锥转换。
对于交流子系统约束,用Iij,ac,2(t)和Ui,2(t)替换式(12)~式(14)以及式(16)和式(17)中的二次项和,可得
将约束条件式(33)做松弛处理,可得
再等价变换成标准二阶锥的形式,有
直流子系统约束转化相似于交流子系统,用Iij,dc,2(t)和Ui,2(t)替换式(18)~式(20)及式(22)和式(23)中的二次项和,可得
将约束条件式(40)做松弛处理,可得
再等价变换成标准二阶锥的形式,有
步骤3储能系统及VSC运行约束的锥转换。
将BESS充放电约束式(1)转换为旋转锥约束为
而式(2)~式(7)为线性约束,无需对其进行转化。
与BESS 充放电约束类似,式(10)中绝对值项转化同式(25)。VSC 的充放电约束需要等价地转换为旋转锥约束,即
至此完成了优化模型的锥转换处理。
本文采用Gurobi工具,利用Matlab求解目标优化模型的锥规划算法。本文提出的内层优化模型求解框图如图2所示。
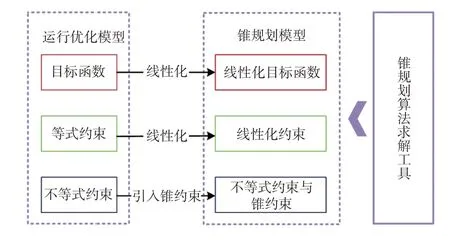
图2 内层优化模型框图Fig.2 Block diagram of inner-layer optimization model
2.2 外层优化模型
外层模型以BESS经济性最优为目标,表示为
式中:Csys、Crep、CFOM、Cdis分别为储能系统的年均初始安装成本、更换成本、固定运维成本和处理成本;CL0为BESS配置前配电系统的年均网损成本。
(1)初始安装成本。本文的储能系统主要包含电池、PCS和相关辅助设施。因此系统的年均初始安装成本可表示为
式中:CE和CP分别为储能电池的单位容量成本价格和单位功率成本价格;Prate,i为第i个储能系统的额定功率;Y为项目年限周期,a;σ为贴现率,%。
(2)更换成本。电池储能在项目周期内的年均更换成本为
式中:k和n分别为储能电池更换的次数和寿命周期;ε为更换储能的电池本体的次数;β为储能初始安装成本每年下降的比例。本文设定PCS 的使用寿命为10 a。
(3)固定运维成本。固定运维成本CFOM与储能类型和额定功率有关,可表示为
式中,Cf为储能系统的单位固定运维成本。
(4)处理成本。处理费用是处理废旧电池所产生的费用为
式中,Cd为电池的单位处置成本。
本文设置储能的额定无功功率为额定有功功率0.5倍。此外,外层优化模型还应满足约束条件
式中:和分别为第i个储能系统投资功率的上、下限;和分别为第i个储能系统投资容量的上、下限。
遗传算法可通过迭代获得优化结果,能够有效解决非线性约束问题,但其易陷于局部最优解;而模拟退火算法可以辅助遗传算法离开局部最优区域,进而寻找全局最优解[19],因此外层优化模型采用遗传算法结合模拟退火算法求解,求解流程如图3所示。
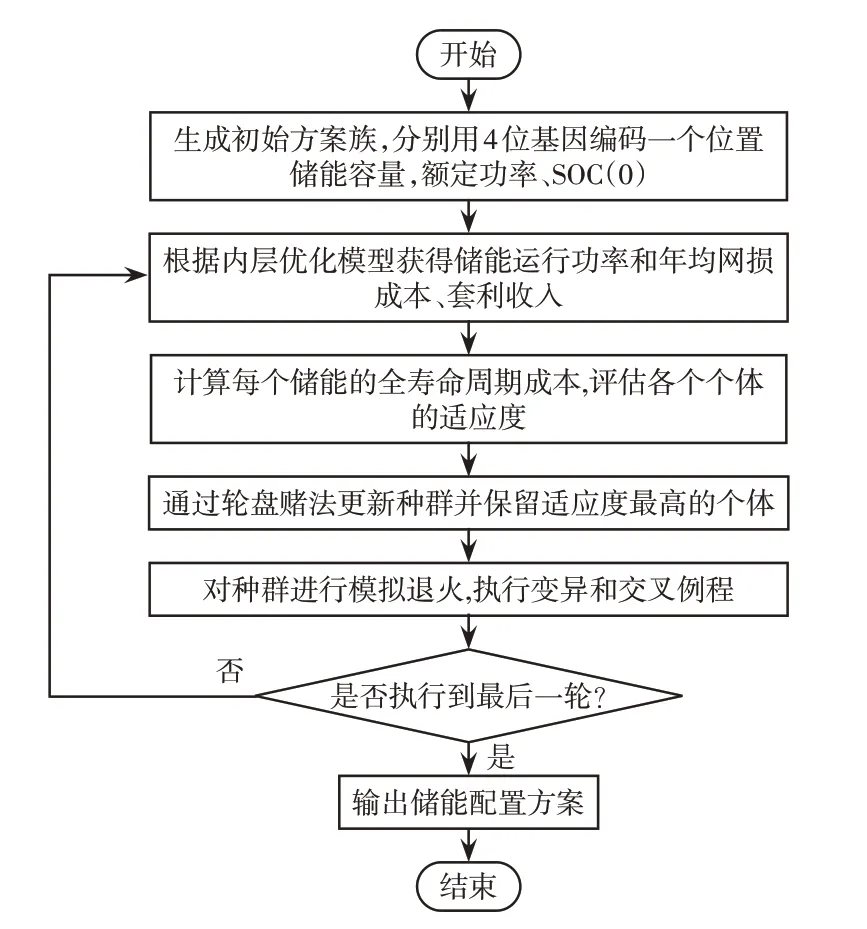
图3 外层优化模型求解流程Fig.3 Flow chart of solving the outer-layer optimization model
3 算例分析
3.1 算例设置
以如图4 所示的低压交直流混合配电系统为例来验证本文所提BESS双层容量优化配置模型的有效性和准确性,相关参数见表1。
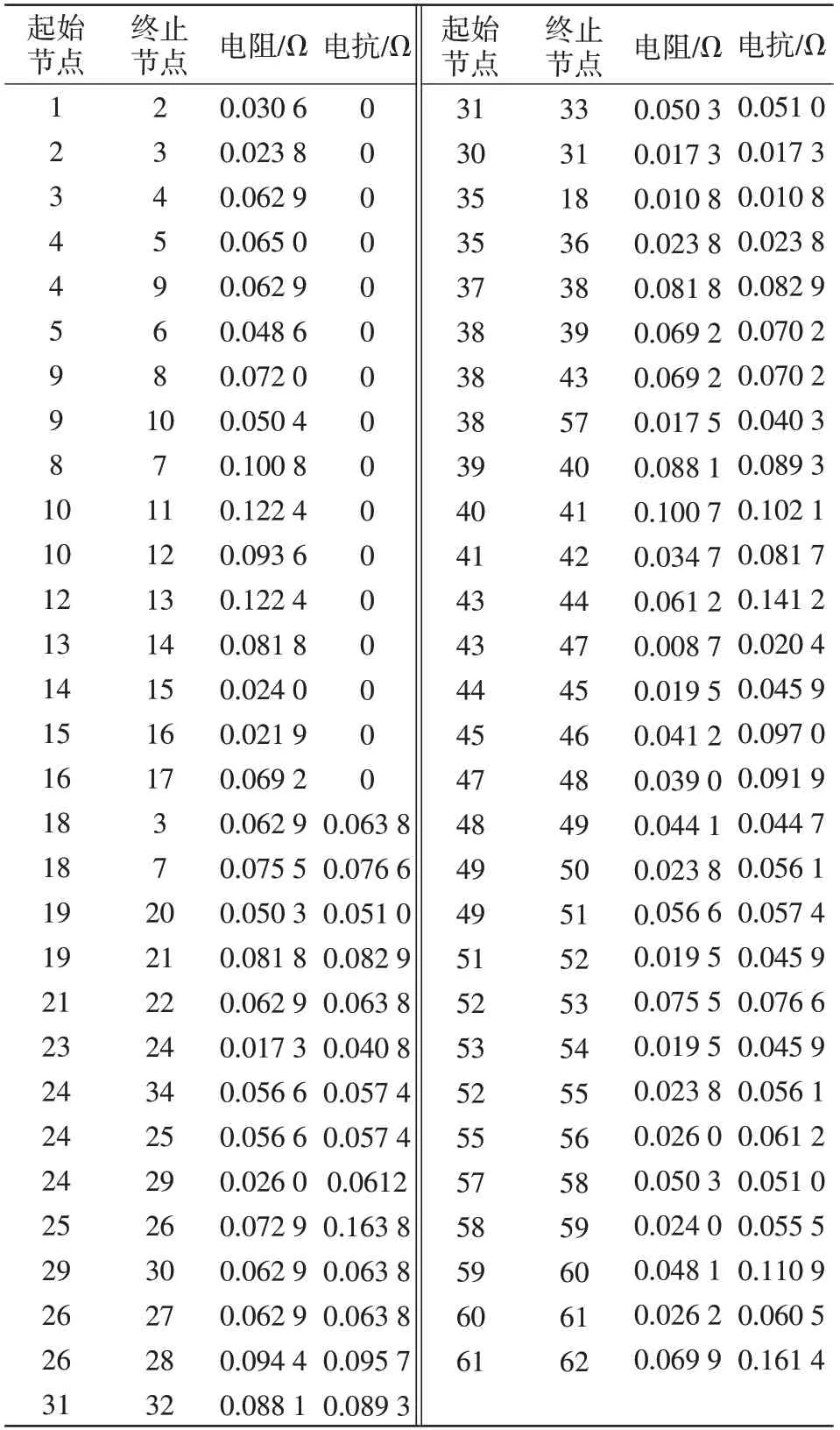
表1 交直流混合配电系统线路参数Tab.1 Line parameters of AC/DC hybrid distribution system
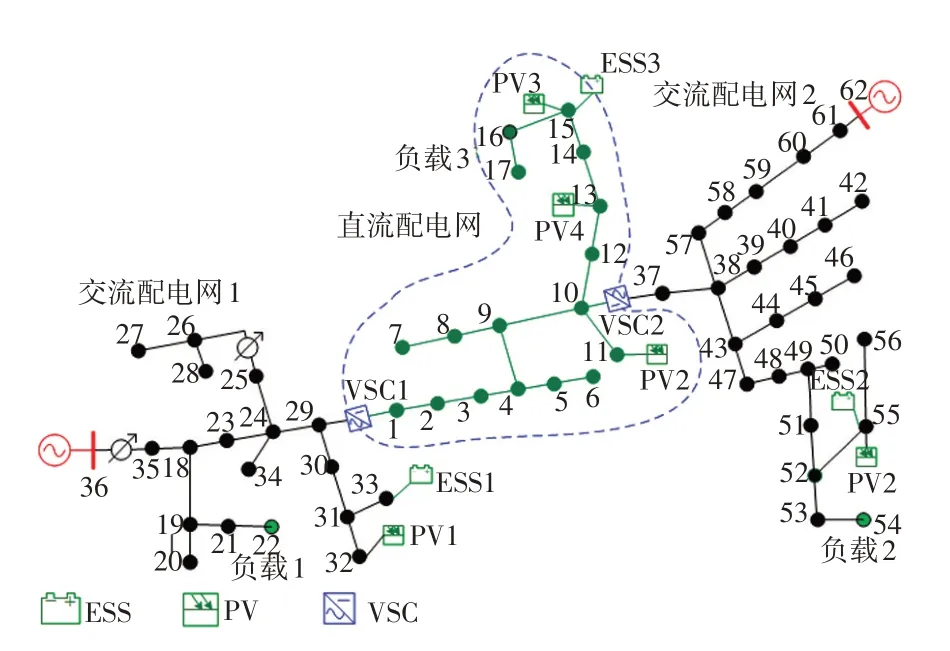
图4 低压交直流混合配电系统结构Fig.4 Topology of low-voltage AC/DC hybrid distribution system
算例中交直流混合配电系统共包含61 个节点,整个系统分为交流配电系统1 和系统2 及直流配电系统3 部分。直流系统中VSC1 控制模式为UdcQ控制,VSC2 为PQ控制模式。交流配电系统1、直流配电系统和交流配电系统2的平衡节点分别为节点36、节点1和节点62。设置交流配电系统和直流配电系统的电压等级为10 kV 和±10 kV,各支路允许通过的最大电流为500 A,电压幅值区间设为[0.97 p.u.,1.03 p.u.],优化区间为[0.985 p.u,1.015 p.u.]。本算例采用峰谷分时电价,具体如表2 所示,各负荷和PV的运行情况如图5所示。

表2 分时电价Tab.2 Time-of-use electricity price
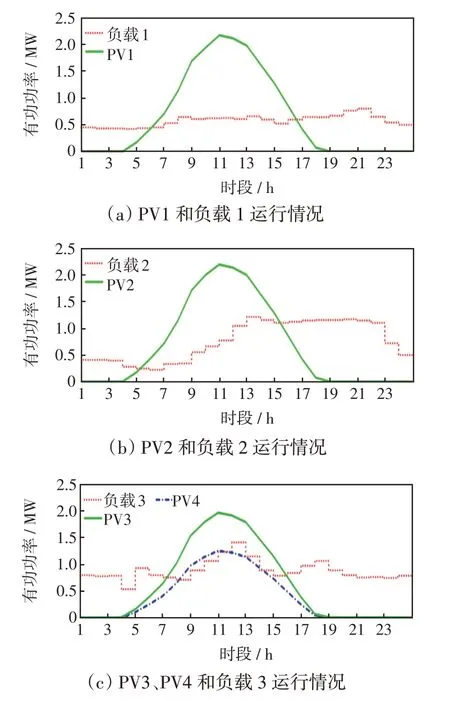
图5 典型日负荷与光伏电源的运行情况Fig.5 Operation of typical daily load and PV power generation
项目规划年限为20 a,单位容量价格、单位功率价格、单位运维成本和单位处理成本分别为1 060 元/(kW·h)、1 085 元/kW、155 元/kW和1 400 元/kW,贴现率设为10%,VSC 参数见表3。通过层次分析法得到目标函数的权重系数λ1= 0.7,λ2=0.15,λ3=0.15[17]。本算例在Matlab环境下调用Gurobi工具进行求解。

表3 VSC 初始配置参数Tab.3 Initial configuration parameters of VSC
3.2 优化结果分析
本算例中BESS 配置结果如表4 所示。为进一步研究交直流混合配电系统中电压水平和经济性受BESS运行策略的影响,设置了以下3种不同场景进行对比分析。
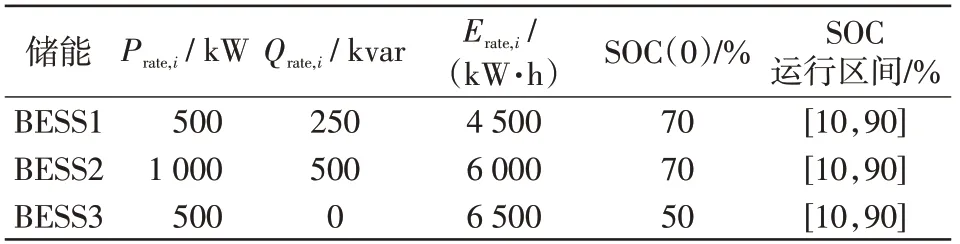
表4 双层容量优化配置模型结果Tab.4 Results of bi-level capacity optimization model
场景1:储能未参与运行,只有VSC 参与系统调节。
场景2:储能仅有功功率参与运行,储能与VSC协调运行参与系统调节。
场景3:储能有功/无功功率同时参与运行,储能与VSC协调运行参与调节交直流混合配电系统调节。
3.2.1 场景1:储能未参与运行
在场景1 中,只有VSC 参与交直流混合配电系统调节。图6和图7中展示了VSC1和VSC2的运行情况以及各个子系统的电压情况。可见,仅VSC1和VSC2 协调运行参与交直流混合配电系统调节,各子系统会出现电压越限问题。在08:00—12:00时段,3 个子系统的电压因PV 出力的增大而升高,其中交流子系统2中的PV位置距离平衡节点较远,其电压变化显著。在13:00—16:00 时段,交流子系统2 的电压越限问题由于负荷的逐渐增加而有所缓解。由于VSC1 采用UdcQ控制且直流负荷靠近VSC2,故VSC2 提供直流配电系统的功率支撑,减轻了直流子系统的电压越限问题。在08:00—15:00 时段,各VSC 调节无功功率以尽可能地缓解电压问题。在17:00—22:00 时段,由于交流子系统2 负荷较重,直流子系统主要由交流子系统1 经VSC1提供功率支撑,且VSC2通过无功支撑缓解交流子系统2电压问题。
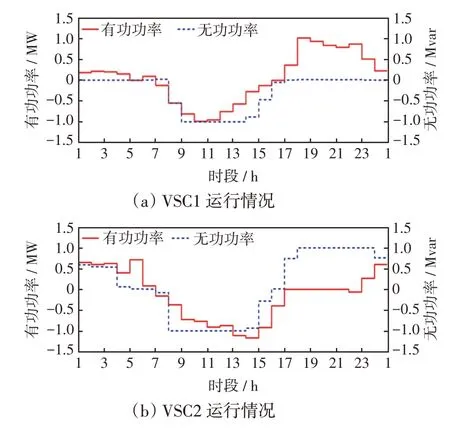
图6 场景1 下VSC 运行情况Fig.6 Operation of VSCs under Scenario 1
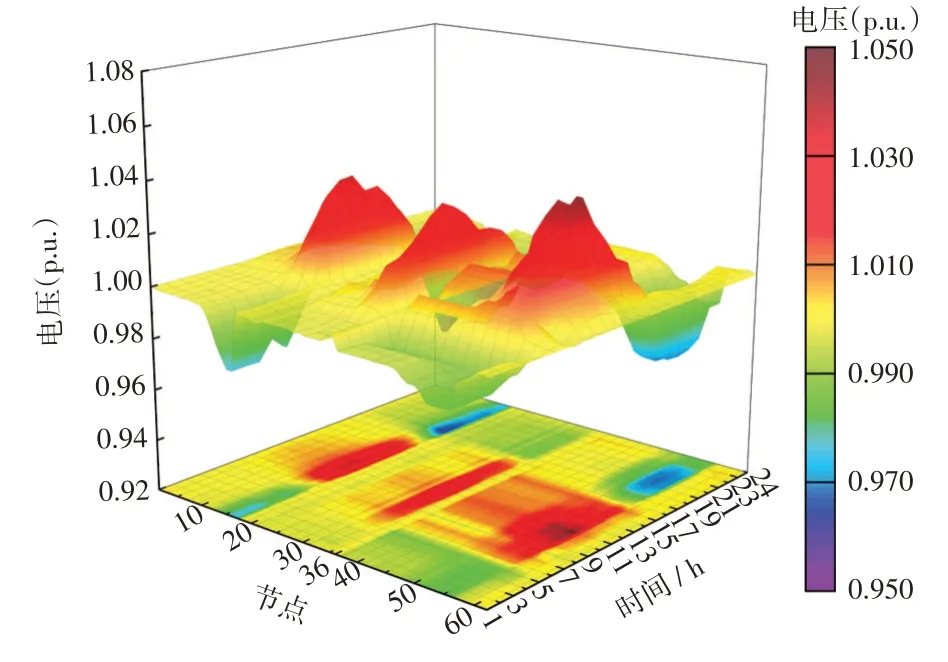
图7 场景1 下各典型节点电压曲线Fig.7 Voltage curve at typical nodes under Scenario 1
综上,VSC的协调运行对交直流混合系统的稳定运行起到积极作用,但VSC的有限容量难以保证极端条件下交直流混合系统的稳定运行。
3.2.2 场景2:储能仅有功参与运行
场景2 下,BESS 的配置结果如表4 所示,各BESS 仅有功出力,将表4 中的额定无功功率QN设定为0。储能与VSC 协调运行以平抑由PV 出力和负荷变化引起的电压问题。各储能系统的运行情况、VSC的运行情况和各子系统的电压水平分别如图8、图9和10所示。

图8 场景2 下储能系统运行情况Fig.8 Operation of BESSs under Scenario 2
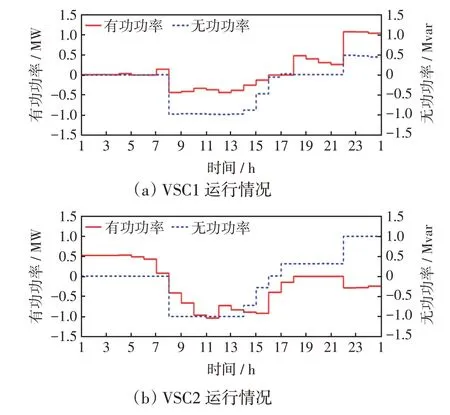
图9 场景2 下VSC 运行情况Fig.9 Operation of VSCs under Scenario 2
由图8~图10 可以看出,通过储能介入可以解决系统电压问题,并且BESS 的充放电状况由系统中的电力供求关系所确定,而储能系统只有在电压安全裕度范围之内才能进行套利。各系统的电压在09:00—15:00 时段越上限,为了将电压的幅值控制在规定的范围之内,储能系统在高电价期间进行充电。综合考虑01:00—05:00 时段和08:00—16:00 时段储能以及VSC 的运行情况,BESS1 除了在电压越限阶段要吸收多余电量之外,其余时段主要处于套利运行状态;而BESS2、BESS3则在低电价时段进行放电,以此来维持储能的充放电量的平衡。从图9可以看出,在08:00—16:00时段,直流配电系统倒送功率主要经由VSC2 被交流配电系统2消纳,由于直流配电系统的PV节点距离采用PQ控制的VSC2 较近,因此直流配电系统的电压能够保持在较好的水平。
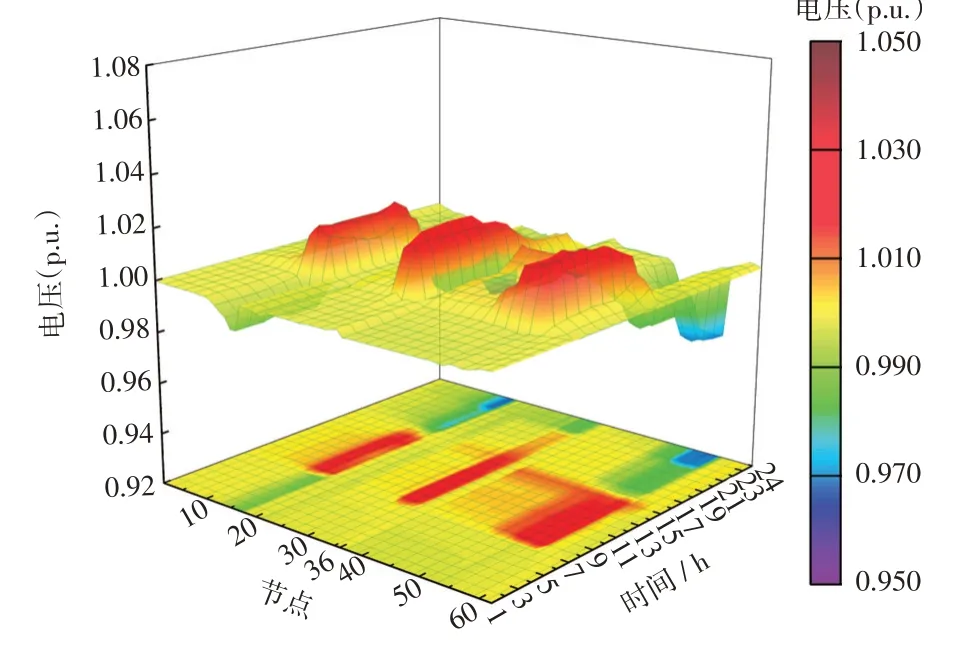
图10 场景2 下各典型节点电压曲线Fig.10 Voltage curve at typical nodes under Scenario 2
综上,VSC与BESS的协调运行,既能保证系统的电压稳定在安全裕度内,又能使储能系统获得套利收益。此外,二者协调运行减少了混合系统对储能的调控需求,从而减少储能的配置容量。当交直流混合系统的电压处于安全电压范围内时,采用PQ控制方式且距离直流负荷较近的VSC将会优先为其提供电力功率支持,以确保直流配电系统的电压处于一个较优的水平。
3.2.3 场景3:储能有功/无功同时参与运行
场景3 中BESS 配置情况见表4。在不改变BESS 配置的情况下,通过调节PCS 功率因数可获得无功支撑。BESS无功调节与有功输出和VSC协调运行相配合,可对系统电压进行更深层次的调节,从而提升BESS套利收益。图11和图12分别展示了BESS 和VSC 的运行情况,图13 展示了各个子系统的电压水平。可见,PCS无功介入后,当PV出力增加引起电压越限时,BESS能够通过其有功/无功功率配合将各系统电压调整到安全范围内,与场景2结果相比各子系统的电压水平得到进一步提高。
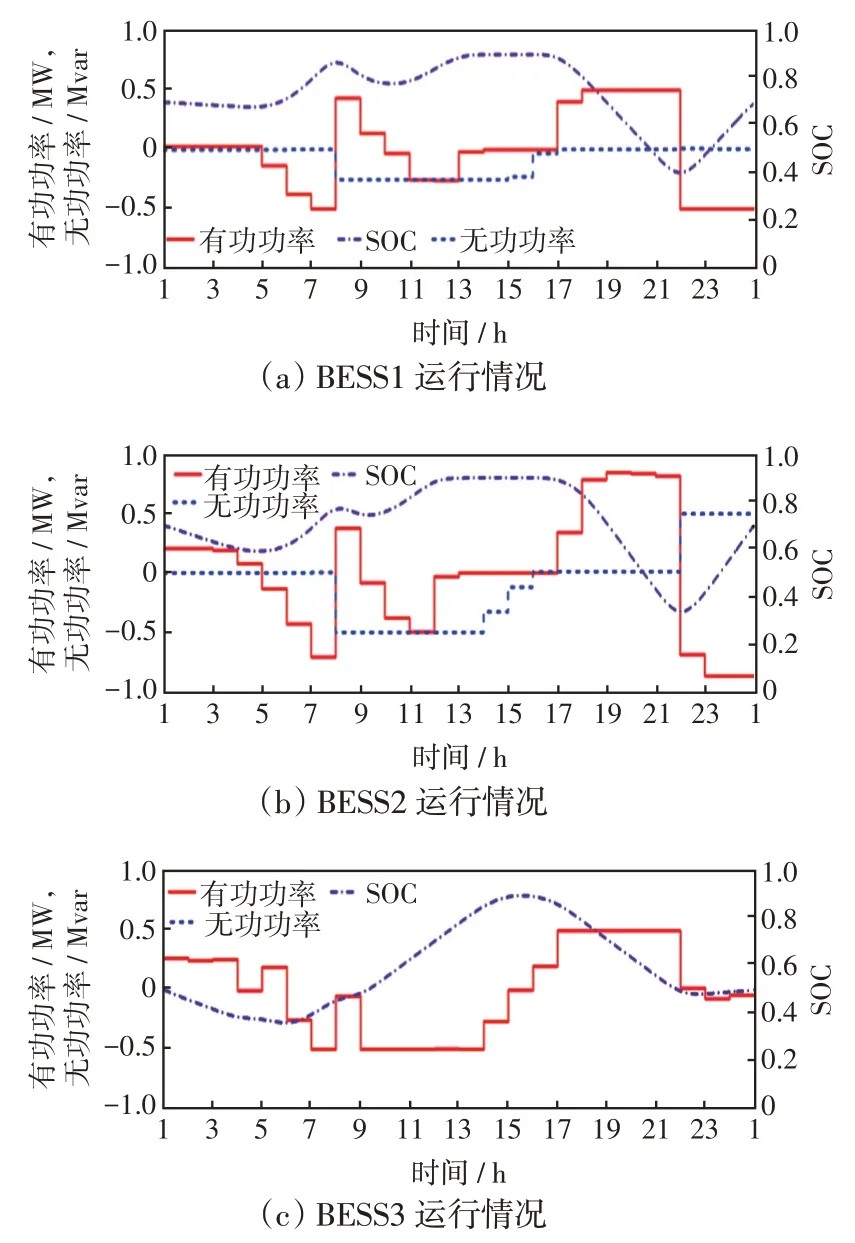
图11 场景3 下储能系统运行情况Fig.11 Operation of BESSs under Scenario 3
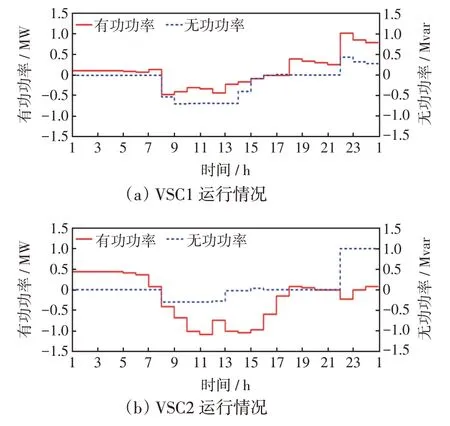
图12 场景3 下VSC 运行情况Fig.12 Operation of VSCs under Scenario 3
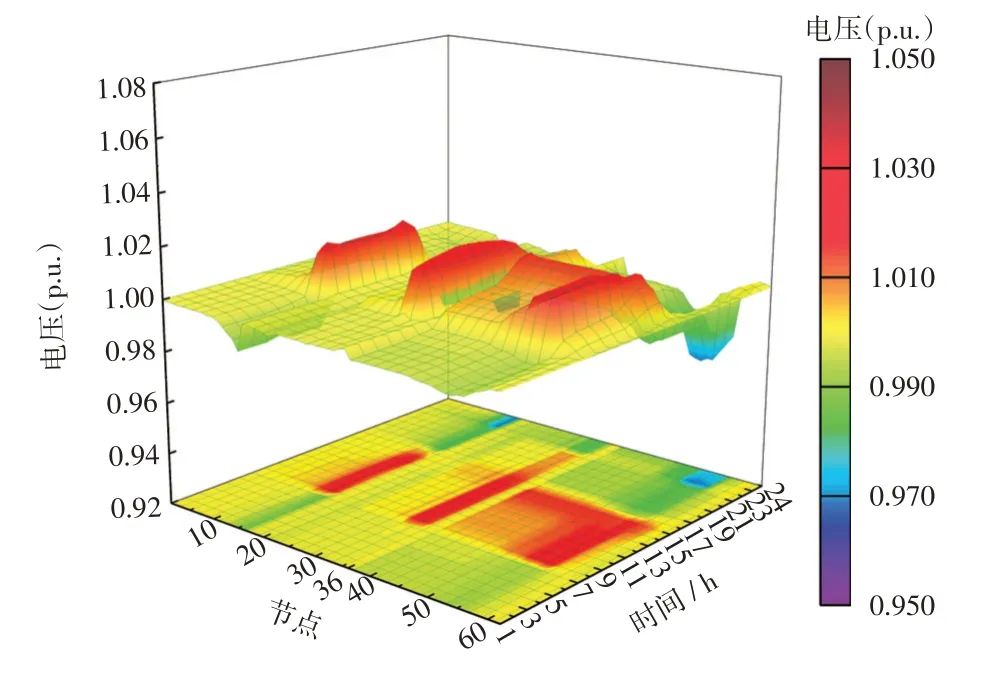
图13 场景3 下各典型节点电压曲线Fig.13 Voltage curve at typical nodes under Scenario 3
与场景2相比,场景3中BESS获得了更好的峰谷套利收益。经过PCS1无功补偿后,VSC1的无功出力减少,实现了无功的就地补偿,提高了系统的电压水平并减少了网络损耗。3个储能双系统协调互动,保持系统在安全电压范围内并实现BESS 收益最大化。
各场景下BESS的套利收益和混合系统的年均网损成本见表5,考虑PCS 无功出力后,BESS 的年套利收入增加约70.9 万元。图14 所示为场景2 和场景3下各BESS年均成本,通过比较在PCS产生无功功率前后各BESS 年均成本变化,可见,BESS1年均成本改变较小,BESS2平均成本增加了约3.2万元,BESS3年均成本减少了约2.3万元。在不同的场景下,各BESS配置情况保持不变,变化成本主要来自更换和处理成本。在综合考虑BESS全寿命周期成本、储能套利收益以及降低网损收益后,与PCS 无功出力之前相比,BESS总年均成本减少了65.4万元。因此,在PCS 无功出力后BESS 的经济性能得到了较大改善。
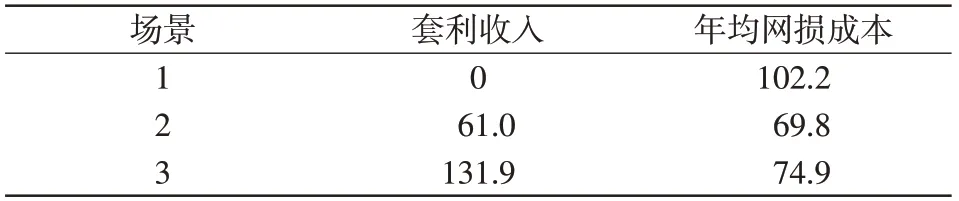
表5 各场景下的套利收益和年均网损成本Tab.5 Arbitrage revenue and average annual loss cost under various scenarios 万元
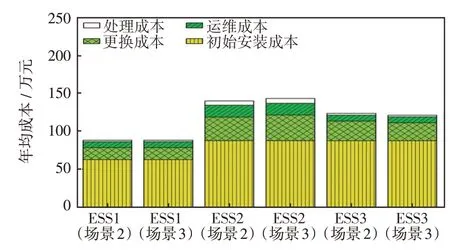
图14 场景2 和场景3 下各储能年均成本Fig.14 Average annual cost of each ESS under Scenarios 2 and 3
综上,充分发挥BESS 有功功率调节能力和无功支撑能力,与VSC 协同运行,可以有效缓解由分布式电源和负荷引起的交直流混合系统电压问题,进而提高配电网对可再生能源的消纳能力。此外,PCS 的无功出力能够增大储能的套利收益并避免冗余配置。
4 结 论
本文面向交直流混合配电系统,提出了一种考虑VSC 和BESS 运行特性的BESS 容量优化配置方法,以适应新能源带来的随机性和间歇性。结论如下。
(1)交直流混合配电系统便于直流电源的接入,各子系统可通过VSC 进行功率支撑,从而提高整个系统的灵活性和可控性。
(2)BESS和VSC联合运行可有效调节系统电压,同时提高整个系统的经济性并避免储能冗余配置。
(3)BESS 可通过改变PCS 的功率因数来实现对电力系统的无功支撑,并与VSC 运行相结合,可实现系统电压的进一步稳定,同时提高BESS 套利收益。
