考虑需求响应及不确定性的综合能源优化调度

2024-03-22赵天悦黄明娟

电力系统及其自动化学报 2024年2期

张涛，田凤，杨航，赵天悦，刘伉，黄明娟

（1.三峡大学电气与新能源学院，宜昌 443002；2.三峡大学智慧能源技术湖北省工程研究中心，宜昌 443002）

在化石能源日益耗竭、环境问题日益严重的今天，兼顾多能互补的区域综合能源系统RIES（regional integrated energy system）成为当前学者研究的热点[1]。综合需求响应作为需求侧管理的一种重要手段，在系统运行中显示出巨大潜力，不仅能够发挥需求侧能源之间的互补作用，还能促进供需互动，调整负荷曲线。目前，国内外学者对考虑综合需求响应的RIES研究已经取得了一定的成果。文献[2]考虑电热负荷的多样性，构建了包含电负荷削减、时移响应和热负荷供能方式响应的综合需求响应，提高了系统的运行效益；文献[3]在综合需求响应的基础上，同时考虑储能及电转气P2G（powerto-gas）设备，对RIES 进行优化，改善系统的经济性和环保性；文献[4]基于电热冷负荷的柔性特性，建立了电热冷需求响应模型，有效降低了负荷的峰谷差。

需求响应通过鼓励用户削峰填谷，使得系统运转更加高效。然而，需求响应的实施需要用户的配合，一般而言，用户满意度越高，参与响应积极性越高。因此，考虑用户满意度已成为许多学者的共识。文献[5]将用户满意度作为约束条件，建立了电气互联系统优化模型；文献[6]基于电价响应协调负荷侧资源，并引入用户满意度约束确保用户参与度；文献[7]提出了考虑用户满意度的激励型需求响应的微网多目标优化模型。上述文献都采用单层规划模型进行求解，在考虑用户侧利益时，只是将用户满意度作为约束之一进行求解，没有进一步分析用户满意度与系统成本之间的内在联系。事实上，用户与系统分属不同的主体，对于不同的利益主体，建立主从博弈模型进行求解是最优的方法。不确定性会给系统运行带来较大影响，由于各种不可抗因素，用户响应量不可避免地具有不确定性。文献[8]采用联合模糊法与概率法解决需求响应的不确定性；文献[9-10]分别采用鲁棒优化和区间优化的方法对需求响应的不确定性进行处理。以上解决系统不确定性问题的方法都是利用历史数据进行分析，没有考虑到用户响应量具有实时变化的特征。当前常用的信息更新方法为贝叶斯方法[11]，它能够根据先验信息和样本信息更新当前的预测信息，且能够不断迭代，提高预测准确性。

综上所述，本文以综合能源系统中的综合需求响应为研究对象。考虑碳交易机制，建立了计及碳排放和P2G 的RIES 模型。为更好地激励用户平缓负荷波动，引入实时定价策略，建立了兼顾系统和用户利益的低碳经济调度主从博弈模型，上层考虑系统运行总成本最小，构建机组出力模型；下层根据上层结果，同时考虑消费者满意度最大和碳排放量最小，构建需求响应参数调整模型，并根据所得结果，更新需求侧负荷曲线，且将此曲线返回给上层进行迭代，直到得到纳什均衡解。针对需求响应的不确定性，引用贝叶斯方法对需求响应量进行更新，并通过算例仿真验证了本文所提模型的有效性，分析了用户满意度对系统优化运行的影响。

1 考虑碳交易的RIES

1.1 RIES 结构

RIES以满足需求侧多种类负荷需求为目标，由多种能源形式、能量转换设备和耦合设备组成[12]。文中构建的RIES 主要由风机、热电联产CHP（combined heat and power）机组、电锅炉、P2G 设备、燃气锅炉以及电气热储能设备等组成，且系统可与上级电网、气网进行能量交换，电气热负荷均通过价格型需求响应参与系统调度。RIES结构如图1所示。

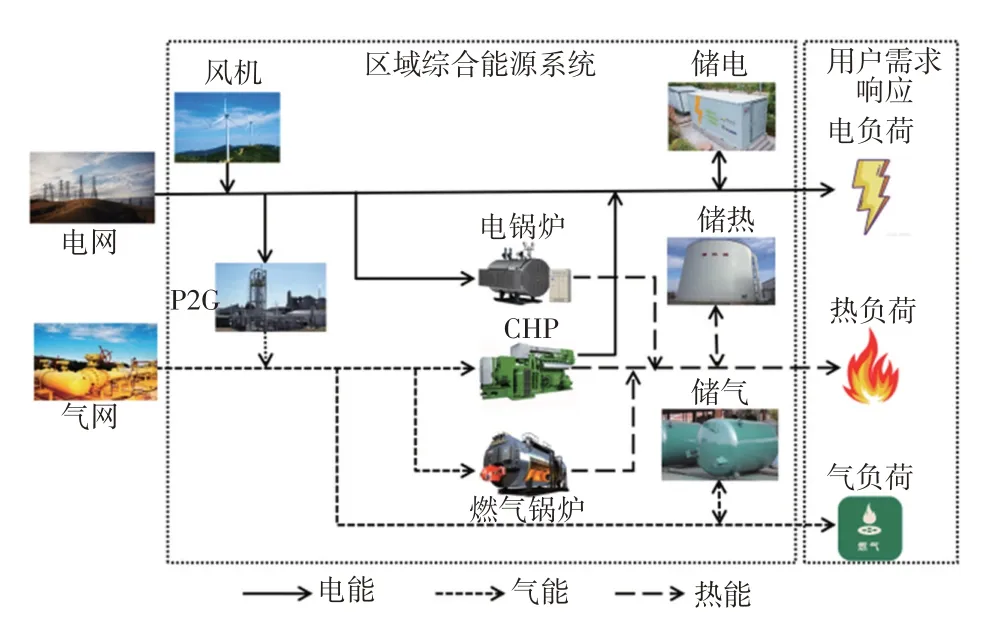
图1 RIES 结构Fig.1 Structure of RIES

为便于分析RIES 中的能量耦合关系，采用能量主线建模思想[13]，将图1 中能量流动关系通过矩阵形式进行描述，即

式中：Pe,t、Pg,t、Ph,t分别为t时段电、气、热的负荷需求；、ηP2G、ηEB、和ηGB分别为CHP 机组产电、P2G 机组、电锅炉、CHP 机组产热、燃气锅炉的效率；PWT,t、PP2G,t、PEB,t、PCHP,t和PGB,t分别为t时段风机、P2G 设备、电锅炉、CHP 机组和燃气锅炉的输入功率；Pgrid,t和Pgas,t分别为向上级电网和气网的购电、购气功率；ΔPES,t、ΔPGS,t、ΔPHS,t分别为t时段电、气、热储能的变化功率；Pqi,t为t时段的弃风功率。

1.2 碳交易机制模型

1.2.1 P2G 碳减排模型

电转天然气主要由电解水和甲烷化两个过程组成，其中，甲烷化的化学方程式为CO2+4H2→CH4+2H2O。由于该过程中需要消耗CO2，所以P2G技术还拥有良好的碳减排能力。P2G设备的耗电量PP2G与生成天然气体积VCH4之间的关系[14]可表述为

式中：PP2G为P2G 机组的耗电量；LHVgas为天然气低热值；VCH4为生成甲烷的体积。

由上述化学方程式可知，生成一定体积VCH4的甲烷时，消耗CO2的量为

1.2.2 碳交易成本模型

碳交易模型参考文献[15]，以初始分配的无偿碳排放权配额为基础，根据实际碳排放量得到参与碳交易市场的碳排放权额度，继而求出碳交易成本，具体描述为

式中：ERIES、ERIES,a和ERIES,r分别为RIES 碳排放权份额交易量、RIES 实际碳排放量和碳排放权配额；λ为碳排放权单位交易价格；CCO2为碳交易成本。

1.3 RIES 调度模型

1.3.1 目标函数

以RIES 运行成本最小为目标，包括购电购气成本、燃料成本、运维成本以及碳交易成本，具体目标函数表示为

式中：F1为RIES运行成本目标函数；Cgrid,t、Cgas,t分别为t时段的购电、购气成本；CG,t为t时段的燃料成本；COM,t为t时段的设备运维成本；CCO2,t为t时段的碳交易成本。

（1）购气、购电成本分别为

式中：pgrid,t、pgas,t分别为购电、购气单价；Pgrid,t、Pgas,t分别为购电、购气功率。

（2）燃料成本为

式中：I为设备总数；Pi,t为t时段设备i的输出功率；ηi为设备i的效率。

（3）设备运维成本为

式中，ki为设备i的单位运维成本系数。

1.3.2 约束条件

（1）能量平衡约束包括电能平衡约束、气能平衡约束以及热能平衡约束，表示为

（2）储能设备约束。本文涉及储电、储气、储热三类储能设备，采用统一的形式进行建模，有

式中：Et和Et-1为t时段和t-1时段的储能设备容量；Pchar,t、Pdis,t分别为t时段的充、放能功率；ηchar、ηdis分别为储能设备充、放能的效率；ηloss为储能设备的自损耗率；σchar,t和σdis,t均为0、1变量，值为1 时分别表示储能设备处于充能、放能状态；值为0时表示停止充能、放能。

（3）常规机组约束。RIES 各设备均有出力上、下限约束，表示为

式中：PP2G,max和PP2G,min为P2G设备的出力上、下限；PCHP,max和PCHP,min为CHP机组的出力上、下限；PEB,max和PEB,min为电锅炉的出力上、下限；PGB,max和PGB,min为燃气锅炉的出力上、下限。

2 综合需求响应不确定性模型

2.1 电气负荷需求响应与满意度模型

2.1.1 电气负荷需求响应模型

本文的电负荷和气负荷需求响应均采用价格型需求响应进行建模。目前常见的定价机制为分时定价。然而实时定价相比于分时定价，通过对每小时的价格进行修改，能够更有效地引导用户改变原有用能方式，达到削峰填谷的目的[16]。

以电负荷为例，对于价格型响应，通常采用电量电价弹性关系进行建模[17]，其表达式为

式中：为电价自弹性系数；为电价交叉弹性系数；pei和分别为i时段的原始电价和电价变化的改变量；pej和Δpej分别为j时段的原始电价和电价的改变量；Qei和ΔQei分别为i时段的原始电负荷和电价变化后的负荷改变量。

2.1.2 电气负荷需求响应满意度模型

用户满意度对于需求响应政策的实施效果具有重要影响。一般认为用户满意度越高，其响应行为更为可靠，相反地，用户满意度越低，越有可能出现不响应的行为。用户满意度的影响因素多样化，包括天气、用能价格、用能质量、服务质量、生活习惯以及家庭行为等。本文主要考虑的是需求响应满意度的影响因素，以电负荷为例，需求响应主要是通过改变各时段电价从而使得用户自发的改变其用电行为的机制，因此，在考虑需求响应的满意度时，主要考虑电价和用电行为的改变对用户满意度的影响，而认为其外在条件如天气、用能质量、服务质量等不变，采用文献[18]中的用户满意度模型进行建模，包括用能方式满意度和用能费用满意度两个指标。

1）用能方式满意度

以电负荷为例，假设在未进行电价调整之前，用户根据个人习惯和偏好进行用电量的安排，认为此时方式满意度的值为1。在进行电价调整后，用户基于费用调整自己的用电量，对负荷曲线进行更新，认为无论用户增加用电量还是减少用电量，用电方式满意度都会降低，可表示为

式中：Mfe为用电方式满意度；为价格调整后的用电量。

2）用能费用满意度

一般根据用户用电总量不变的规则来制定实时价格，然而在实际运行中，改变电价后的用电总量与改变前完全一致基本上是不存在的。如果用户没有对调整后的实时价格进行响应，可能会严重影响到用电费用，用电费用越大，用户用电费用满意度越小，用电费用越小，用户满意度越大，用电费用满意度可表示为

式中：Mce为用电费用满意度；为调整后的电价。

2.2 热负荷需求响应与满意度模型

2.2.1 热负荷需求响应模型

人们对热负荷有感知模糊性，尤其是在舒适区间内，用户对其敏感性偏低。温度是其主要调节参数，温度的改变并不会对用户造成很大的冲击[3]。本文基于此，建立热负荷需求响应模型。

采用文献[19]的模型，建筑物室内温度与供暖功率、环境温度的关系为

式中：Tin,t和Tout,t分别为t时段的建筑物室内温度和室外温度；R为建筑物的等效热阻；cair为建筑物室内空气热容；Qt为t时段建筑物的热功率。

根据人体舒适度的温度区间，对建筑物室温的约束表示为

式中，Tmin和Tmax为室内舒适温度的最低值和最高值。

2.2.2 热负荷需求响应满意度模型

人体对温度的变化并不是很敏感，因此，在一定范围内调整热负荷，并不会改变用户对周边温度的感知，本文采用平均标度预测PMV（predicted mean vote）来表征用户对热负荷的满意度。针对不同的PMV，用户的主观感受如表1所示。

表1 用户感受与PMV 指标对应关系Tab.1 Relationship between user feelings and PMV indicator

由表1 可知，当PMV 介于-1 到1 之间时，用户的热满意度较高。文献[20]给出了PMV 指标与室内温度的计算关系，即

式中，mh为热用户满意度。

2.3 考虑贝叶斯理论的需求响应模型

用户参与需求响应受到多种因素的影响，响应量具有不确定性，贝叶斯理论正是处理上述不确定性问题的有效手段。区别于传统需求预测方法，贝叶斯方法能够在先验信息的基础上，将样本信息纳入考虑，从而对当前的响应信息进行更新，降低需求响应误差，提高需求响应可靠性[21]。

根据贝叶斯公式，需求响应量X的先验概率密度函数f（x）为

式中：E为需求响应的期望；fE(e)为期望的概率分布密度函数；fX|E=e(x)为需求响应的条件概率分布。

系统不断收集用户响应量的信息，获得需求响应观测值，记为X=Xe=，其中Xe为观测的需求响应量。使用每次收集到的实际值对原来用户需求响应期望E不断进行更新，在给定X=时有

式（20）即为响应期望的后验概率密度函数，记为。根据它再对X的概率分布进行更新，就可以得到需求响应的后验概率分布，即

由此，需求响应改变量可调整为

3 RIES 双层调度模型

在需求响应策略中，RIES与用户分属不同的利益主体。一方面，RIES总是期望自己的运行成本越低越好；另一方面，用户在实际用能中期望自己的用能满意度越高越好，而改变价格方式，满意度总是会有所降低，这就需要在费用满意度中有所弥补。因此，用户总是希望自己的用能费用越低越好，这对于系统侧而言，却代表系统侧运行成本的增长，因此，系统侧与用户侧之间的利益是相互冲突的，应找到一个均衡解去平衡两者之间的利益。可以将用户侧与系统侧之间的关系看做主从博弈关系，即系统侧为领导者，首先做出决策，用户侧为追随者，根据上层决策得出最有利的决策；然后系统侧再根据用户侧的决策进行决策。如此反复，直至均衡。

双层规划理论是解决主从博弈问题的常见方法，它通过上下嵌套的结构，能够有效平衡不同利益体之间的优化目标[22]为

式中：F(x,y)和f(x,y)分别为上层和下层的目标函数；Q(x,y)≤0 和H(x,y)=0 分别为上层的不等式约束和等式约束；q(x,y)≤0 和h(x,y)=0 分别为下层的不等式约束和等式约束。

3.1 博弈流程

步骤1在给出原始电、气价格及室内温度后，电、气、热的负荷也就确定了，系统侧首先根据原始负荷曲线制定最初的调度计划。

步骤2将上层求解到的调度计划作为已知条件，运营商根据用户侧目标函数，得到电、气实时价格以及室内温度。

步骤3将新的实时参数代入电、气、热负荷需求响应及贝叶斯理论的计算公式，得到新的用户侧负荷曲线，从而系统侧再依据新的负荷曲线得出成本最小的调度计划。

步骤4重复步骤2 和3，直到博弈均衡，此均衡解即为运营商最终定下的参数。

博弈框架如图2所示。

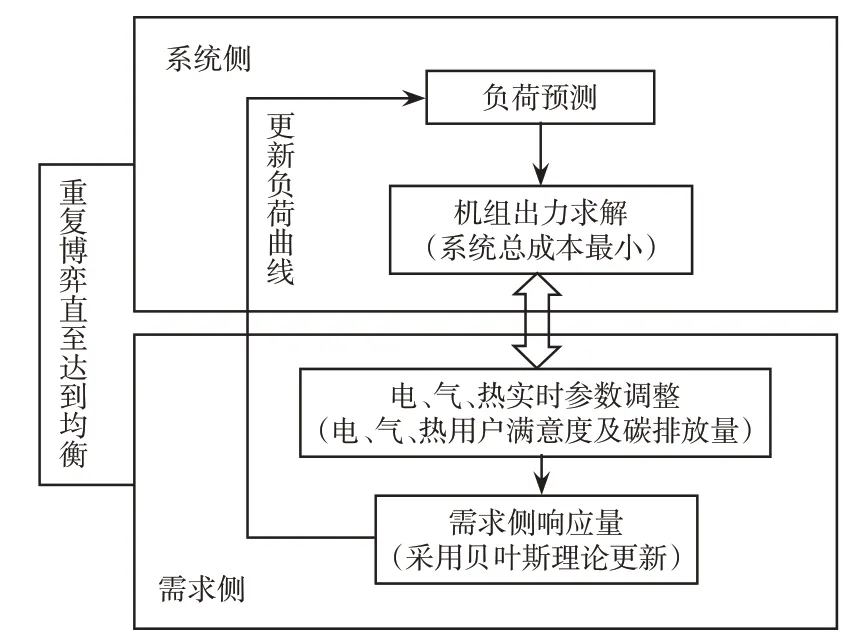
图2 博弈框架Fig.2 Game framework

3.2 考虑综合需求响应的RIES 调度模型

需求响应能够对负荷曲线进行削峰填谷，提高机组利用效率，有利于降低系统运行成本。RIES具有多能互补的特点，其内部的电力系统、热力系统和天然气系统能够实现灵活的耦合互动，本文考虑电、气、热3种负荷具备的柔性特性以及响应能力，发挥系统内部的能源转换和替代能力，挖掘各种负荷的响应潜力，具体见式（5）～式（12）。

3.3 下层需求响应参数调整模型

价格型需求响应是通过价格引导用户改变原有的用能方式，实现削峰填谷的一种手段，然而在实际应用中，用户是否能够按照系统侧所期望的那样平移峰谷负荷取决于用户的满意度大小，因此在建立下层需求响应参数调整模型中，应将用户侧利益纳入考虑。

3.3.1 目标函数

用户侧利益通过用户行为给自己带来的影响来体现，主要包括两方面，即个人利益和集体利益。个人利益即用能行为对用户生活质量的影响，集体利益主要考虑为用能行为对用户生活环境的影响。所以下层目标函数为多目标函数，一方面考虑用户用能满意度最大，另一方面考虑碳交易成本最小，具体表示为

式中：和Mcg分别为气能的用气方式满意度和费用满意度；和分别为需求响应前和响应后的碳交易值。

3.3.2 约束条件

（1）调整量约束为

式中：pe和pg分别为需求响应前电价和气价；p′e和分别为需求响应后电价和气价；Δpe,max和Δpg,max分别为电和气价格调整量的最大值；Qgi、分别为价格调整前、后的气负荷量；Qhi、分别为价格调整前、后的热负荷量；、、分别为电、气、热负荷调整量的最大值。

（2）供需平衡约束，用户在参与需求响应后，仍然满足系统能量平衡约束，同式（9）。

3.4 模型求解

上述博弈模型的下层是一个多目标模型，通过加权模糊化将下层模型转化为单目标函数，即

式中：μ(Fi)为隶属度函数；Fi为目标函数；和分别为目标函数的最大值和最小值；λ1和λ2为两个目标的权重。

4 算例分析

为了验证本文所提出模型的有效性，基于文献[3，23-25]中的数据进行算例仿真。对应的负荷和风电预测出力曲线如图3 所示。各设备参数如表2 所示。本文建立的双层模型上层采用CPLEX求解器进行求解，下层为非线性问题，因此考虑采用蒙特卡洛算法进行求解。

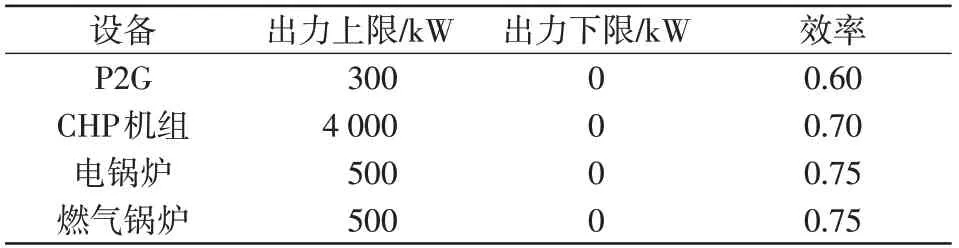
表2 设备参数Tab.2 Parameters of devices

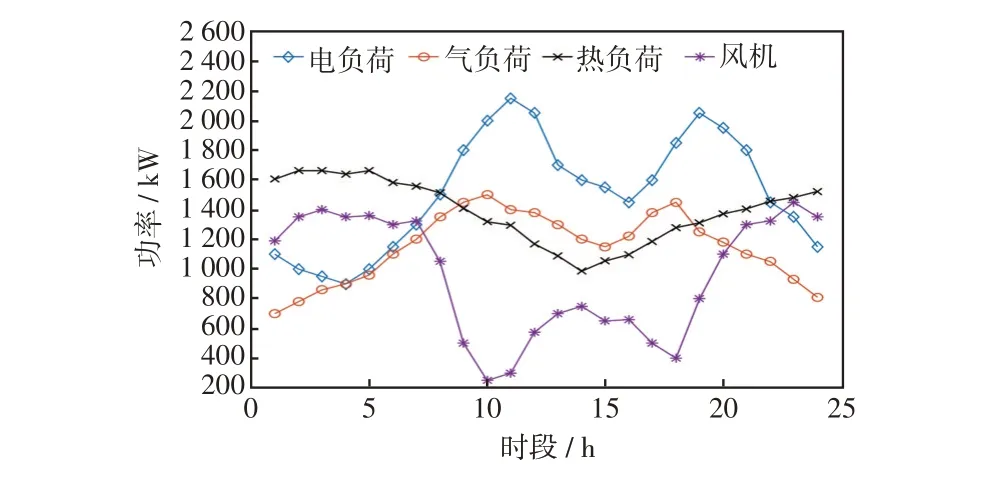
图3 负荷和风电预测出力曲线Fig.3 Curves of loads and forecasted wind power output

为验证本文所提模型的优越性，本文设置了如表3 所示的3 种场景进行仿真。表中，√表示考虑了该因素，×表示没考虑该因素，假设场景1的用户满意度为初始值1。

表3 场景分类Tab.3 Classification of scenarios

4.1 不同调度情景的对比分析

本文根据设置的3 种对比情景，得到对应的系统运行结果如表4所示。其中，用户满意度一列的括号内的数字表示用户满意度经过归一化处理之后的值。

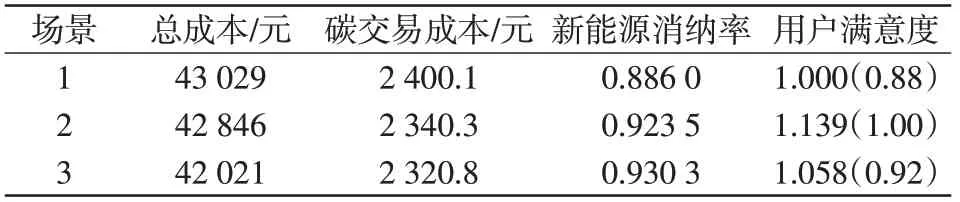
表4 不同场景的结果Tab.4 Results under different scenarios

从表4 可看出，场景2 在场景1 的基础上，采用本文所提需求响应模型，并考虑用户侧利益，采用单层模型进行求解，求得的总成本以及碳交易成本较场景1的都有所下降，原因在于需求响应模型能将负荷进行平移，提高系统设备的利用率。场景2的用户满意度较之场景1的有提高，这是因为用户通过需求响应，降低了用能费用，且费用满意度的提高幅度大于方式满意度的降低幅度，使得总满意度提高。场景3 在场景2 的基础上，采用本文所提双层模型进行求解，从结果可以看出，场景3 的用户满意度和系统成本较场景2的均有所下降，证明本文所提模型能够综合考虑用户满意度和系统运行成本，达到系统与用户双方利益的平衡。

4.2 调度结果分析

图4和图5分别给出了电、气、热需求响应参数改变量和需求响应模型前后电、气、热负荷量的对比。

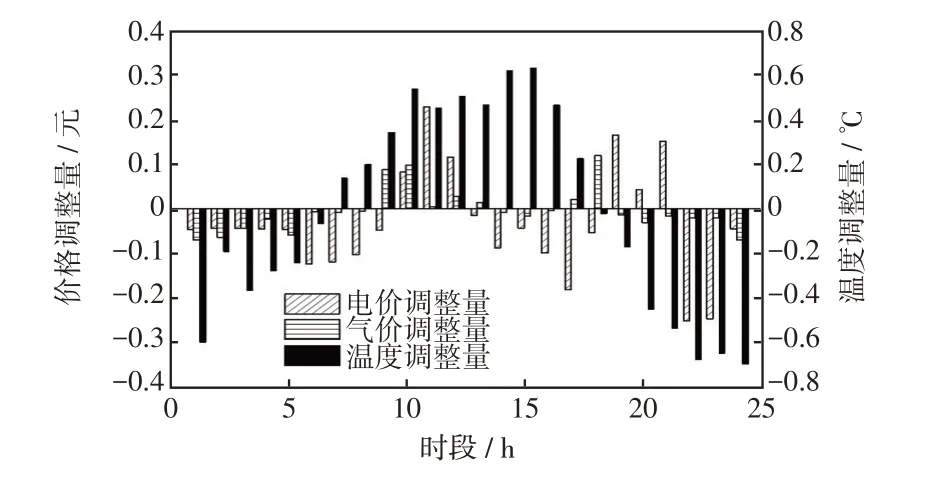
图4 电、气、热需求响应参数改变量Fig.4 Changes in electricity,gas and heat demand response parameters

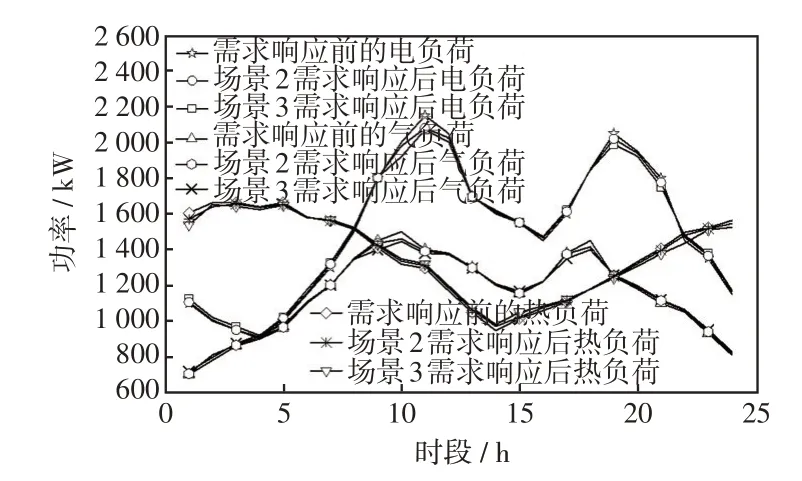
图5 需求响应前后电、气、热负荷量对比Fig.5 Comparison of electricity,gas and heat loads before and after demand response

由图4和图5可见，采用实时定价后，电、气、热负荷都能够在低负荷时段通过改变相应的参数引导用户增加用能量，而在高负荷时段引导用户减少用能量。可以看出，场景3的需求响应模型削峰填谷的趋势较场景2 更明显，即用户的满意度最高，需求响应削峰填谷的趋势越小。场景3 需求响应电、气、热负荷相比需求响应前的峰谷差分别下降了7.8%、15.7%、6.3%。相较于分时定价划分3个时段来改变参数，实时定价每个时段的参数改变量都不相同，且在用能峰谷值附近，参数改变量的幅度更大，验证实时定价对用户需求响应行为的激励性效果更佳。

图6 给出了贝叶斯前后响应误差量的对比。由图6可见，以需求响应公式计算出的响应量为基础，运用贝叶斯方法对响应量进行修正，使得需求响应量的趋势有所缓和，能够降低响应量，即用户参与响应的量并没有达到设定值，这对系统运行而言，主要表现在需求侧负荷曲线削峰填谷趋势的平缓使得系统的经济性变差，但更符合负荷实际情况，验证了使用贝叶斯方法对需求响应量进行更新，能够降低需求响应的不确定性，提高系统运行可靠性。

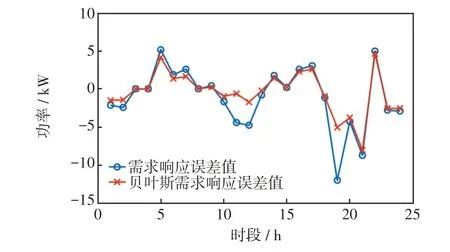
图6 贝叶斯前后响应误差量对比Fig.6 Comparison of response errors before and after the use of Bayesian approach

4.3 需求响应对系统运行的影响

图7 和图8 分别给出了场景2 和场景3 的电调度结果。

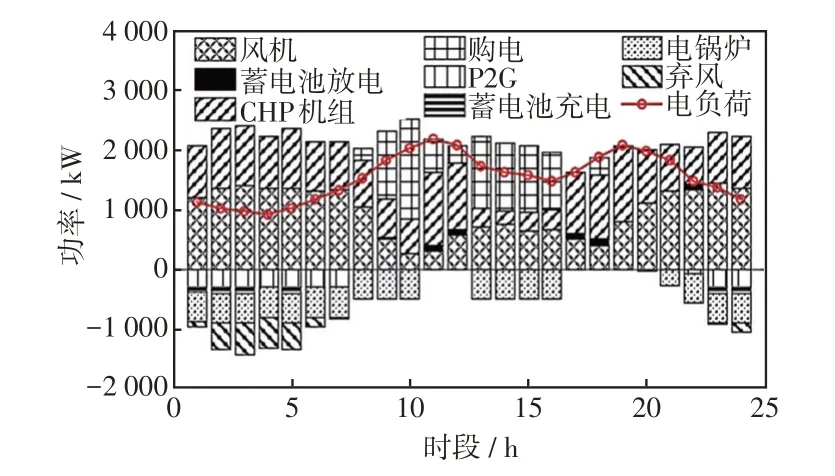
图7 场景2 电调度结果Fig.7 Electricity dispatching results under Scenario 2

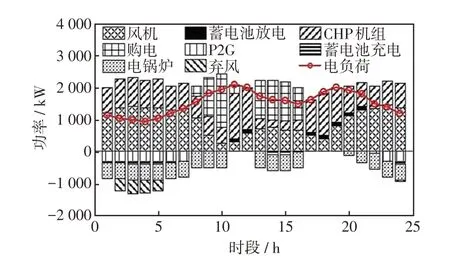
图8 场景3 电调度结果Fig.8 Electricity dispatching results under Scenario 3

对比图7 和图8 可知，图8 的购电量及弃风量均比图7 的少，这是因为图8 采用双层模型进行求解，牺牲了部分用户满意度，使得图8 的负荷曲线较图7 削峰填谷的趋势更明显。高峰时段负荷量的降低可以减少购电量，提高系统的经济性，而低谷时段负荷量的增加可以提高风电的利用率，减少弃风。同时也验证了双层模型对于系统经济性和用户满意度的平衡作用。

图9 和图10 分别给出了场景3 的气、热调度结果。对于气负荷，由图9 可见，本文所提模型能够对气价进行调整，在负荷高峰时段提高价格，负荷低谷时段降低价格，从而引导负荷曲线改变。这对于系统侧而言，能够降低系统成本。在低气价时段（1～5 h，23～24 h），由于气负荷较少，而此时热负荷较多，系统优先采用燃气锅炉进行供热，其余部分采用CHP机组进行供热，储气设备也在此时充气以备在气价高时放气来减少系统成本，在高气价时段（8～12 h，17～18 h），通过需求响应减少该时段气负荷以降低系统成本。

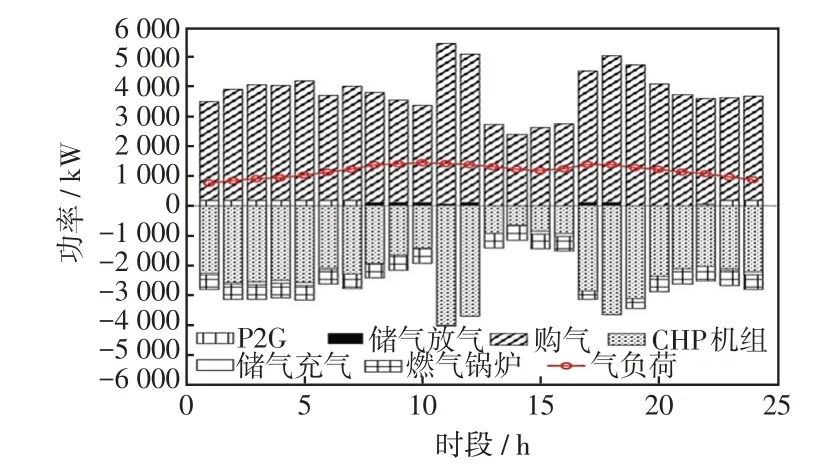
图9 场景3 气调度结果Fig.9 Gas dispatching results under Scenario 3

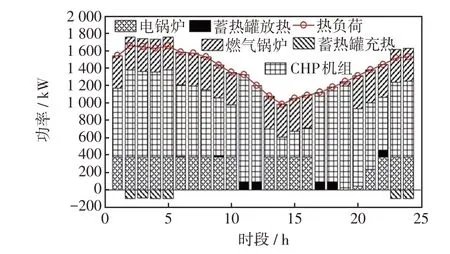
图10 场景3 热调度结果Fig.10 Heat dispatching results under Scenario 3

热负荷如图10 所示，系统供给热能的来源只有电锅炉、燃气锅炉、CHP机组、储热设备。由于没有热网可以购热，所以系统的热能供给不仅与热负荷需求有关，也与电、气能源价格有关。在1～5 h时段，23～24 h 时段，由于室外温度较低，此时热负荷需求较大，而此时电、气能源价格正好处于低谷，所以，优先通过电锅炉和燃气锅炉对负荷进行供给。且储热设备充热以备在电、气价格较高时段通过放气来减少系统成本。

4.4 满意度对结果的影响

考虑P2G机组及综合需求响应，对需求侧电气价格及室内温度赋予不同的参数，采用单层模型进行求解，然后将此参数下求得的用户满意度进行归一化处理后的值作为横坐标，对应的系统运行成本作为纵坐标，并将各点进行拟合得到满意度与成本的关系曲线，如图11所示。

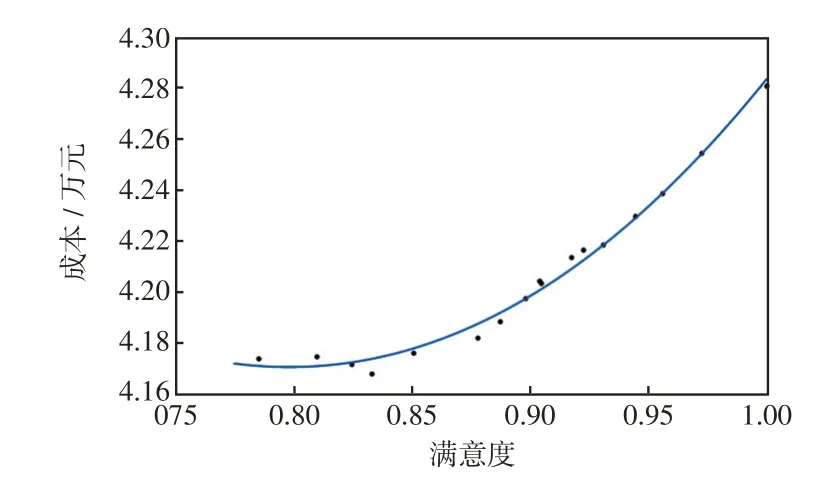
图11 满意度与成本的关系Fig.11 Relationship between satisfaction and cost

由图11 可以看出，在满意度小于0.85 时，系统运行总成本趋于稳定，变化不大，这说明当满意度较低时，用户参与需求相应的意愿不强，需求相应的效果不明显；当用户满意度大于0.85 时，随着用户满意度的提高，系统成本也越来越大，且曲线的斜率逐渐增大，这说明在此范围内，用户参与需求响应的效果越来越明显，需求响应能够有效调节需求侧资源，改变用户的用能方式。同时也说明用户的利益与系统的利益相互冲突，有关部门可以根据当地实际情况选择一个均衡解以平衡系统的利益与用户的利益。根据图11 可知，均衡解应位于0.85～0.95之间。其中，本文所提双层模型最终求得用户满意度为0.92，既通过较高用户满意度保证了需求响应政策实施的可靠性，也保证了系统侧成本不至于太高，可以为今后系统决策提供一定参考。