Effect of Cosmic Plasma on the Observation of Supernovae Ia

Yi-Jia Zheng

National Astronomical Observatories, Chinese Academy of Sciences, Beijing 100101, China; zyj@bao.ac.cn

Abstract In observational cosmology,a supernova Ia is used as a standard candle in order to extend the Hubble diagram to a higher redshift range.Astrophysicists found that the observed brightness of high redshift supernovae Ia is dimmer than expected.This dimming effect is considered observational evidence for the existence of dark energy in the universe.It should be noted that this conclusion is based on an assumption that the mass density of the cosmic plasma is very small.Therefore,the dimming effect caused by the Compton scattering of free electrons in cosmic plasma can be neglected.X-ray observations suggest that the mass density of the cosmic plasma may be very large.In theory,the observed dimming effect of high redshift supernovae Ia may be caused by the Compton scattering of free electrons in the cosmic plasma.In this paper it will be shown that this idea is reasonable.Therefore,there is no need to introduce the confusing concept of dark energy into cosmology.

Key words: Cosmology – cosmology: observations – cosmology: theory – (cosmology:) dark energy –(cosmology:) distance scale – X-rays: diffuse background – plasmas – opacity

1.Introduction

In observational cosmology, a supernova Ia is used as a standard candle in order to extend the Hubble diagram to a higher redshift range.Astrophysicists have found that if cosmic space is a free ocean of radiation (Peebles 2017), and the luminosity distance dLof a high-redshift supernova Ia is only a linear function of its redshift z (i.e., dL=cz/H0), the observed brightness is dimmer than expected (Riess et al.1998;Perlmutter et al.1999).

To explain the observed dimming effect, Perlmutter et al.(1997,1999)proposed that due to the accelerating expansion of the universe, for high redshift supernovae Ia, their actual luminosity distance is greater than that calculated by linear Hubble’s Law, i.e., dL>(cz)/H0.Therefore, observers will receive less energy from high redshift supernovae Ia and leading to the observed dimming effect.

They proposed that the luminosity distance dLof a celestial object not only depended on its redshift z,but also depended on dark energy density ΩΛ, the mass density ΩMand Hubble constant H0(Carroll et al.1992; Perlmutter et al.1997; Riess et al.1998; Perlmutter et al.1999; Sullivan et al.2011).Anyway,the luminosity distance dLis a very complex function of their redshift z, dark energy density ΩΛ, mass density ΩM,and Hubble’s constant H0.See Perlmutter et al.(1997) p.566 for a detailed description of this relationship.The luminosity distance dL=cz/H0applies only approximately to small redshift objects.

To explain the accelerating expansion of the universe, in Perlmutter et al.(1999) they introduce a concept called cosmological-constant energy density, i.e., ΩΛ.Due to its special properties, in Perlmutter (1999), the cosmologicalconstant energy density ΩΛis renamed dark energy.Today,the term dark energy has been accepted by most astrophysicists.

In Perlmutter et al.(1999),based on 60 observed supernovae Ia, they concluded that in order to explain the observed apparent magnitude of the high-redshift supernova Ia, there must be a lot of dark energy (ΩΛ≃0.72 and with negative pressure) in the universe.So far, no physicist has been able to come up with a plausible explanation for dark energy.The existence of an unexplained dark energy phenomenon poses a serious challenge to the Standard Model of cosmology and particle physics(Peebles&Bharat 2003).This is a fatal flaw in the ΛCDM model of the universe.

Observations show that in today’s universe, most baryons still exist in the form of hot ionized gas and permeate the vast space; The total mass density of baryons could be very high(Wang&McCray 1993;Fukugita et al.1998).In theory,due to the Compton scattering effect caused by free electrons in the cosmic plasma, observers will receive less energy from highredshift supernovae Ia and will result in a dimming effect.

Obviously, the observed dimming effect can be explained simply and reasonably by the Compton effect caused by free electrons in the cosmic plasma.Why do most astrophysicists prefer the explanation for the accelerating expansion of the universe caused by mysterious dark energy?

The crux of the matter is that according to the popular ΛCDM cosmological model, most astrophysicists believe that the mass density of cosmic plasma should be very small(much less than the critical mass density of the universe, i.e.,Ωb∼0.05, refer to Perlmutter 1999; Peebles & Bharat 2003;Planck Collaboration 2014).Therefore, in the popular ΛCDM cosmological model, the Compton scattering effect caused by free electrons in the cosmic plasma is usually ignored(the S–Z effect is an exception, refer to Sunyaev & Zeldovich 1980).

The assumption that the mass density of cosmic plasma must be very small is based on a conjecture that the observed CMB is a remnant of the early hot universe, a conjecture proposed by Gamow et al.in the 1940s.According to scenario of Gamow et al.,the temperature of baryons in the universe today should be too low for plasma to exist.Therefore, cosmic space is a free ocean of cosmic microwave background radiation.This scene obviously conflicts with the real universe.Therefore, the unreasonable assumptions of Gamow et al.should be discarded.

Abandoning Gamow et al.ʼs conjecture means that cosmic space is not completely transparent to radiation due to the presence of cosmic plasma.The optical depth of cosmic space is proportional to the luminosity distance of the object being observed.Only for nearby objects, the optical depth caused by the plasma of cosmic space is small and negligible.As the luminosity distance dLincreases,the optical depth of space also increases.Therefore, for a high-redshift supernova Ia with a large luminosity distance dL, the optical depth of the cosmic space is not negligible.

This paper proposes that the observed dimming effect of supernovae Ia can be explained by a reduction in the energy received by observers from high redshift supernovae Ia due to the Compton scattering effect caused by free electrons in the cosmic plasma.

The numerical results show that this suggestion is reasonable and can well explain the dimming effect of high redshift supernovae Ia observed when the mass density of cosmic plasma is large enough.This means that the observed supernova dimming effect cannot be used as strong observational evidence for the existence of the puzzling dark energy.

2.Definition of Apparent Magnitude and Absolute Magnitude

The definitions of apparent and absolute magnitudes for supernovae are the same as those for stars.In order to calculate the observed dimming effect of a supernova Ia due to Compton scattering, it is necessary to review the definition of the apparent magnitude and absolute magnitude of a star:

where M is absolute magnitude of a star, F is the received energy flux from the observed star, F0is the measured energy flux of the same star when it is assumed to be at the 10 pc distance.

This means that at different luminosity distances, the variation in apparent magnitude of a star is determined by the variation in the energy flux received from the star.In a flat universe, the equation for calculating the flux of energy received from a star as a function of luminosity distance is

where dLis its luminosity distance, its unit is 10 pc.

In cosmology,10 pc as the unit of the luminosity distance dLis too small.Usually,the unit of luminosity distance dLis Mpc.So Equation (1) becomes

According to Hubble’s law, the luminosity distance of a celestial object dLis only a linear function of its redshift(Hubble 1929),

So in cosmology, to describe the relation between the apparent magnitude and absolute magnitude of an object,Equation (3) becomes (Perlmutter et al.1997)

This equation is the one used by Perlmutter et al.(1999) to calculate the expected apparent magnitudes of the observed supernovae Ia.Riess et al.(1998)and Perlmutter(1999)found that the observed apparent magnitudes of high redshift SNe Ia are larger (darker) than that calculated by Equation (4).

3.The Compton Scattering Effect Caused by Cosmic Plasma

X-ray observations suggest that there may be large amounts of plasma in the vast expanse of cosmic space.Just because“on theoretical grounds, however, it is difficult to see how there could be much mass in void plasma,” such observational evidence has been ignored by most astrophysicists (Wang &McCray 1993; Fukugita et al.1998).

Due to the presence of cosmic plasma, the radiation will interact with free electrons in the cosmic plasma and scatter the incident radiation in other directions (Compton scattering effect) (Sunyaev & Zeldovich 1980).Therefore, cosmic space cannot be a free ocean for radiation, as Gamow et al.believed(Peebles 2017).For an observed object with a luminosity distance of dL,the optical depth,caused by Compton scattering of free electrons in cosmic plasma, is

where σcis the Compton scattering cross-section of a free electron,Ne is the mean number density of free electron in the cosmic plasma.

Considering the Compton scattering effect, the energy flux received by the observer will be attenuated, which can be expressed as

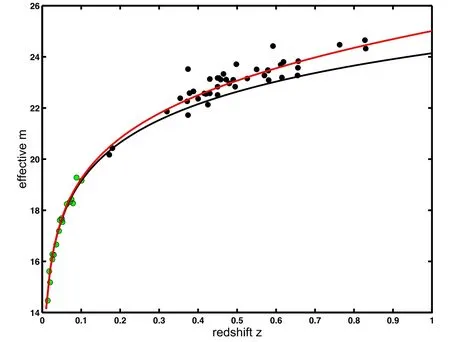
Figure 1.Hubble diagram for 60 type Ia supernovae and models fitting.The effective peak magnitudes of SNe Ia come from column (9) in table 1 (black spots) and table 2 (green spots) in Perlmutter et al.(1999).The red solid line corresponds to the calculation of Equation(9).The black solid line corresponds to the calculation of Equation (4) (i.e., not calculating the energy loss factor 2.5 log (e xp( -z))causedbythecosmic plasma).In the calculations, Hubble constant H0=72.5 km s-1Mpc-1 and the absolute magnitude of SNe Ia M=-19.02.

where F(τ(dL)=0)is the observer received energy flux without considering the cosmic plasma attenuation effect.

Therefore,considering the Compton scattering effect caused by free electrons in cosmic plasma, Equation (2) should be modified as

This equation can also be used to calculate the apparent magnitude of low redshift objects, because in the z ≃0 region τ ≃0.In this case, Equation (7) returns to Equation (2).Equation (4) should be modified as

For 60 observed supernovae Ia listed in Perlmutter et al.(1999), numerical estimations show τ(dL)≃z.Therefore,Equation (8) can be modified as

Figure 1 shows the magnitude-redshift relation of high redshift supernovae Ia.It includes the effective magnitudes of 60 redshift SNe Ia and the theoretical curves calculated according to Equations (4) and (9) The effective peak magnitudes of SNe Ia come from column (9) in table 1 (black spots)and table 2(green spots)in Perlmutter et al.(1999).The red solid line corresponds to the calculation of Equation (9).The solid black line corresponds to the calculation of Equation (4).

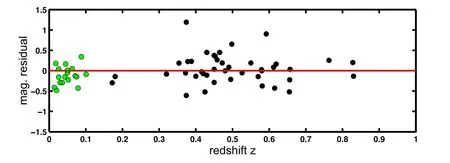
Figure 2.Magnitude residuals fitted by the models in Figure 1.

In the calculations of Equations (4) and (9) the parameters used are: H0=72.5 km s-1Mpc-1, the absolute magnitude of SNe Ia M=-19.02.Figure 2 shows the magnitude residuals fitted by Equation (9) (i.e., the red solid line in Figure 1).

From Figures 1 it can be seen that the observations of the high redshift SNe Ia cannot be fitted by the black solid line.This is because the black solid line is calculated using Equation (4) and the Compton scattering effect caused by free electrons in the cosmic plasma are not included in the calculations.This is why Riess et al.(1998) and Perlmutter et al.(1999) found that the observed apparent magnitudes of high-redshift SNe Ia are larger (darker) than that calculated using formula (4).

The observations can be fitted well by the red solid line.This is because the red solid line is calculated using Equation (9)and the Compton scattering effect caused by free electrons in the cosmic plasma are included in the calculations.This means that the observed dimming effect of high-redshift supernova Ia can indeed be explained simply and reasonably by the Compton scattering effect of free electrons in the cosmic plasma.

4.Discussion

As can be seen from Figures 1 and 2,the observed dimming effect of high-redshift supernovae Ia can indeed be explained simply and reasonably by the Compton scattering effect of free electrons in the cosmic plasma.This means that if the mass density of the cosmic plasma was not unreasonably limited to a small value, there would be no need to introduce mysterious dark energy into cosmological models to explain the observed dimming effect of high-redshift supernovae Ia.

Why have most astrophysicists not proposed Compton scattering to explain the observed dimming effect of highredshift supernova Ia?The crux of the matter is that in popular ΛCDM model, the baryonic mass density of the universe is limited to a very small value (Ωb<0.05).Therefore, most astrophysicists believed that Compton scattering effect caused by free electrons in cosmic plasma is negligible.

In the ΛCDM model, why is the baryon mass density of the universe limited to a very small value? This is because in the ΛCDM model,it assumes that the observed CMB is a remnant of the early hot universe,which was proposed by Gamow et al.in the 1940s.According to scenario of Gamow et al., the temperature of baryons in the universe today should be very low.Therefore, there should be no plasma in space, and space should be a free ocean of radiation (Peebles 2017).

Gamow et al.and most astrophysicists believe that the observed perfect blackbody spectrum of the CMB comes from early cosmic thermal radiation.If cosmic plasma exists in space, then the CMB’s interaction with the cosmic plasma would disrupt the CMB’s original spectrum without preserving the perfect blackbody spectrum observed today (Sunyaev &Zeldovich 1980).In order to minimize the influence of cosmic plasma, in the popular ΛCDM cosmological model, the mass density of cosmic plasma is limited to a small prior value(Planck Collaboration 2014).

Observations of the diffuse soft X-ray background suggest that the mass of the cosmic plasma may be very large(Wang&McCray 1993).It is only because Fukugita et al.argued that:“On theoretical grounds, however, it is difficult to see how there could be much mass in void plasma,”this component was unreasonably omitted and not accounted for in their cosmic baryon budget (Fukugita et al.1998).This means that in the real universe, a large amount of cosmic plasma can indeed coexist harmoniously with the observed CMB with a perfect blackbody spectrum.

In order to remove the restriction on the mass density of cosmic plasma,it is necessary to explain why a large amount of cosmic plasma can coexist harmoniously with the observed CMB with a perfect blackbody spectrum.One possible and intriguing theory is that the observed CMB is not a remnant of thermal radiation from the early hot universe; It is simply the result of a thermal balance between low-frequency cosmic radiation and cosmic plasma (Zheng 2021).

This means that there is no theoretical or observational basis for assuming that the mass density of cosmic plasma must be very small.In contrast, the presence of cosmic plasma with a greater mass density in the universe would be more reasonable and reliable.The observed dimming effect of high-redshift supernovae Ia can be explained simply and reasonably by the Compton scattering effect caused by free electrons in the cosmic plasma.

As can be seen from Figure 1,when the redshift value of the observed object is small, it is difficult to detect the dimming effect caused by cosmic plasma.As the redshift of the observed object increases, so does the dimming effect caused by the cosmic plasma,which gradually becomes easier to detect.This is why the dimming effect caused by cosmic plasma was only discovered after the Hubble map was expanded to a higher redshift range (Perlmutter et al.1999).

The idea that there is a large amount of cosmic plasma in the universe is also consistent with the fact that the gravitational mass density can consist of a variety of fully ionized gases.This means that there is no need to introduce large quantities of unknown non-baryonic dark matter into the universe(Wu 2000; Xue & Wu 2002; Zheng 2023).

5.Conclusion

The assumption that “the baryonic mass density of the universe must be very small” is the fatal flaw of the popular ΛCDM cosmological model; Discarding this false assumption,the dimming effect of high redshift supernovae Ia can be explained simply and reasonably by the Compton scattering effect caused by free electrons in the cosmic plasma.This means that there is no need to assume the existence of confusing dark energy in the universe.