可变检测信道的民用无人机遥控信号检测方法*

王 维，王红林，申 江

（1.电子科技大学 物理学院，四川 成都 611731；2.成都九洲迪飞科技有限责任公司，四川 成都 610041）

0 引言

近年来，随着民用无人机的普及与发展，其市场规模不断扩大，给国民经济的发展带来巨大利好，但也使得公共安全维护面临巨大的挑战。因此，业界对无人机的探测与防范技术，研究也从未间断，总的说来分为雷达技术、光电技术、声波识别和无线电探测几个方面[1]。其中雷达技术在面对“低小慢”目标时，由于受体积、飞行高度和速度等因素的影响，探测性能下降，而光电技术和声波识别技术受到探测距离的限制，同时也容易受到环境噪声的影响。因此，无线电频谱检测技术在无人机探测上还是处于主力军位置[2]。

民用无人机的遥控信号大多采用跳速不高（60～80 Hops/s）、跳频信道不多（10～50 个）的跳频通信技术。对于跳频信号的检测与识别，通常采用时频分析的手段，文献[3-6]采用短时傅里叶变换（Short-Time Fourier Transform，STFT）的分析方法，且在大信噪比（典型＞6 dB）的情况下，能取得较好的检测效果。在工程实践中，短时傅里叶分析主要采用加滑动时间窗的快速傅里叶变换（Fast Fourier Transform，FFT）方法。因此信号检测的频率分辨率和频点主要由信号采样率Fs和选取的变换点数N决定，一旦Fs和L确定后，所能检测的频点位置就会随之固定下来，并且L必须为2 的整数次幂。在这种限制下，传统的短时傅里叶变换检测方法可能会带来检测频点与实际频点出现偏移的现象及处理资源浪费的问题。为解决上述问题，本文提出一种可变检测信道的民用无人机飞控信号检测方法，以及其在FPGA 中的具体实现方法。

1 可变信道的无人机信号检测算法

1.1 基于Goertzel 算法的跳频信号检测及其改进

为实现检测信道的任意可变，首先，假设待检测信号为已知的单一频点，实现对单一信道的检测；其次，根据具体所需检测的信道进行资源例化；最后，覆盖所有需要检测的频点。对于单一频率的检测，本文选择高效的Goertzel 算法来实现，通过对该算法结构进行改进，以实现实时的信号检测功能。

Goertzel 算法是由杰拉德·格策尔提出的，用于高效估计区域离散傅里叶变化的一种方法。该方法以二阶IIR 滤波器的形式出现，具有两个实反馈系数和一个前馈系数，如图1 所示。

图1 Goertzel 算法的IIR 滤波器实现

IIR 滤波器可以用于计算总数为N的频率单元离散傅里叶变换中第m个频率单元的DFT 结果，计算过程如下：

式中：X(m)表示DFT 的输出结果，x(n)表示DFT的输入信号。

根据式（1）对每N个输入时间采样信号，计算出一个复数DFT 的频率单元值。为了能够在每个输入采样点时刻输出一个频率值，需要对原始的Goertzel 算法进行改进。本文采用滑动窗的形式，计算一个在滑动窗内基于时间样值的N点DFT 的单个频率单元结果。对于N点DFT 中的第m个频率单元，SDFT 的计算公式为：

式中：Xm(q)表示第m个频率单元的DFT 结果，x(n)表示输入信号。

将式（2）进行变换，可以得到SDFT 型IIR 滤波器结构的表达形式：

式（3）的实现结构如图2 所示。

图2 单频率单元SDFT 滤波器结构

单频率单元SDFT 算法通过一个带有梳状滤波器和复合谐振器的IIR 滤波器实现。其中，梳状滤波器不区分频率，可以作为公共驱动部分，复合谐振器中的复乘数因子ej2πm/N根据所检测的频率值m不同而确认。如果需要检测多个频率，则只需复制多个复数再生器即可。第m个信道检测的频率为m×Fs/N。SDFT 检测的输入x(n)为实信号序列，输出的结果为X m(n)复信号序列。为得到被检测信道的功率值，还需要计算复信号的幅度|X m(n)|。

SDFT 算法与普遍使用的STFT 算法（主要使用FFT 算法实现）相比，在民用无人机跳频信号检测方面的优势主要体现在以下几个方面：

（1）N不必为2 的整数次幂；

（2）谐振频率可以是0 到Fs之间的任意值；

（3）可任意添加m个检测信道（m≤N）；

（4）滤波器系数（相对FFT 旋转因子）的存储量较少；

（5）计算之前无须存储所有的输入数据。

1.2 跳频信号干扰消除与二值化判决

民用无人机的遥控信号一般在工业、科学和医学（ISM）频段工作，因此对民用无人机遥控信号的检测方面，将面临其他工业设备的干扰。从干扰设备数量和功率上来看，对无人机跳频信号侦测干扰最严重的是Wi-Fi 信号。为提高无人机跳频信号的检测准确度，需要排除Wi-Fi 信号的干扰。

Wi-Fi 信号使用的是OFDM 调制方式，虽然其子载波数量和具体的频点可能会发生变化，但是在一定时间内频点不会发生跳变，因此可以将Wi-Fi信号看成定频干扰。定频信号和跳频信号的区别在于：在一定时间内，定频信号的瞬时功率约等于平均功率，跳频信号的瞬时功率大于或小于平均功率，因此本文通过设定动态检测门限的方法来去除定频干扰。

基于跳频信号的特征，可以采用功率对消的思想来进行快速判决。

步骤1：确定一个检测窗口，并计算检测窗口内的信号平均功率。由于跳频信号在检测窗口内是非连续存在的，而定频干扰和噪声是连续存在的，因此检测窗口至少要大于一个跳频信号的持续时间，文中检测窗口取2 个跳频信号的持续时间，即包含跳频信号存在和不存在2 段时间。

步骤2：用信号瞬时功率减去平均功率，判断功率差值的符号。如果符号为正则判断为1，表示存在跳频信号；如果符号为负则判断为0，表示不存在跳频信号。

步骤3：对二值化的跳频信号进行时长判决，剔除噪声和猝发信号的干扰。设置跳频信号时长阈值，仅记录超过该阈值的连续信号，对未超过的值进行剔除处理。本文将时长阈值设定为无人机典型跳频周期的2/3。

2 算法仿真及FPGA 实现

2.1 算法仿真

针对本文提出的可变检测信道民用无人机跳频信号检测方法的有效性和工程可实现性，分别使用MATLAB 和Modelsim 工具进行M 文件算法和Verilog 代码仿真。仿真条件为：ADC 采样率=240 Msps，检测信道总数N=240（信道间隔1 MHz），跳频点数=4（F1～F4，分别位于信道1、20、30、40），定频干扰频率数为2（一个碰撞干扰频率F3，位于信道30；一个带内非碰撞干扰频率F5，位于信道50），信噪比为-10 dB。MATLAB 仿真结果如图3 所示。

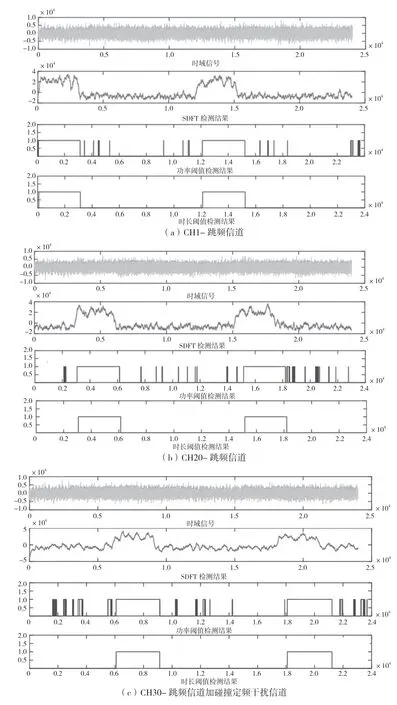
图3 SDFT 检测算法仿真结果

图3（a）～图3（f）分别显示了各信道的输入、过程及最终检测结果，包括：ADC 时域输入信号、SDFT 信道检测结果、跳频信号二值化判决和跳频信号时长判决的结果。从图3 中可以看出，在信噪比为-10 dB 时，算法可以正确解出跳频信号，同时在有定频干扰的跳频信道及仅存在定频信号、噪声的情况下，均未出现误判的情况。

2.2 FPGA 实现及仿真

基于可变信道的无人机跳频信号检测算法用FPGA 实现时，主要需要注意3 个方面的处理。一是在求信号功率时，可以使用快速拟合算法，节省FPGA 的乘法器资源；二是在求平均功率时，为节省逻辑资源，需要对检测功率进行降采样处理；三是在对IIR 滤波器的极点值ej2πm/N做量化处理时要防止溢出震荡。

式中：Xm(n)表示第m个频率单元输出的幅度值，α和β表示系数值，abs(·)表示取绝对值，I和Q分别表示实部和虚部。

通过仿真可以得到，当α取0.990，β取0.197 时，最大的拟合误差为5.33%，能够满足检测需求。

（3）由于SDFT 中有反馈回路，而且极点位于单位圆上，因此ej2πm/N值的精度对结果有很大影响。在对ej2πm/N的值进行Q比特量化时，并执行向下取整，即ceil(ej2πm/N×2^(Q-1))，进而保证极点处于单位圆以内，防止IIR 滤波器溢出而产生震动。

在整个算法实现中，信道数量N、检测窗口长度L和量化位数Q存在性能和资源的平衡，参数越大检测性能越好，同时消耗资源越多。在信道数量N=240，检测窗口长度L=256，量化位数Q=24 的条件下，对FPGA 实现的RTL 代码在Modelsim 仿真软件中进行仿真（输入信号SNR=-10 dB），仿真结果及资源占用情况（使用XC7K410T）如图4 所示。

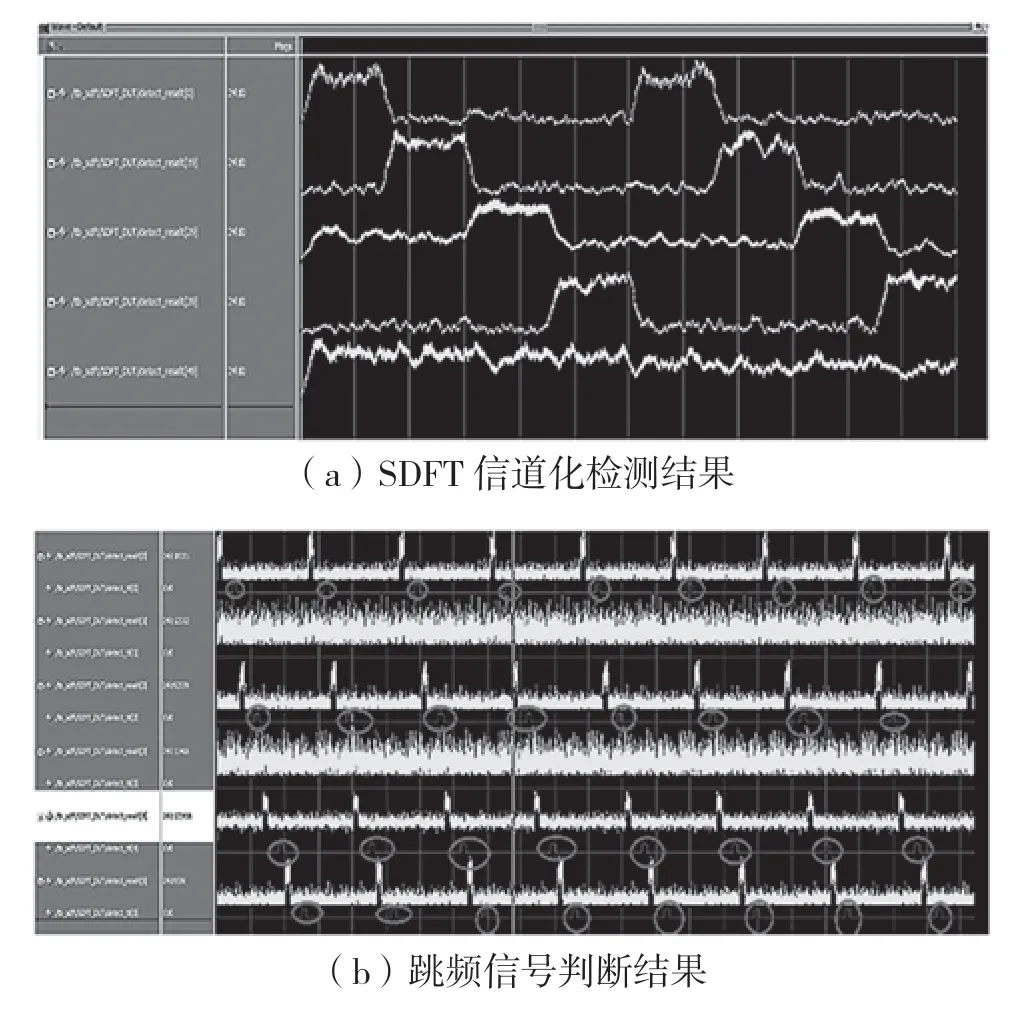
图4 FPGA 实现仿真结果及资源占用情况

从图4 可以看出，本文提出的基于可变检测信道的民用无人机跳频信号检测方法，可以较好地实现对民用无人机跳频信号的实时检测，并输出二值化的时频图案。在240 个检测信道的情况下，FPGA 的逻辑资源和乘法器资源分别占用28%和26%，具有较高的资源利用率。

3 结语

本文针对民用无人机的遥控信号检测提出了一种可变信道的SDFT 快速检测算法，并对该算法进行了FPGA 实现和仿真。该算法的优势在于可以根据实际需求，任意增加或裁剪检测信道，且不受传统FFT 算法点数的限制。仿真结果表明，该方法在低信噪比和存在定频干扰的情况下仍然能够很好地实现跳频信号检测的性能，具有较好的工程实用价值。