自持续HIRS 辅助的MU-MISO 系统公平性研究*

赵丽娟，张 毅

（重庆邮电大学 通信与信息工程学院，重庆 400065）

0 引言

为了满足未来信息社会的通信需求，需要研究下一代移动通信系统6G 技术，以此跟进时代的步伐[1]。智能反射面（Intelligent Reflecting Surface，IRS）作为一种新兴技术，因其可重构无线传播环境的特性，在6G 通信领域具有不可或缺的地位[2]。IRS 中的每个反射元件都能够以期望的方式反射电磁信号，从而人为地创造有利的传播条件，进而提高无线通信系统的信道增益。根据反射元件能否放大入射信号，IRS 可分为被动IRS 和主动IRS。

被动IRS 仅反射入射信号，大多数研究假设被动IRS 的功耗可以被忽略[3-4]。然而，文献[5]指出，被动IRS 的功耗与反射元件的数量有关。在被动IRS 辅助的无线通信系统中，IRS 可以通过外接电源或电池供电，以此来维持其正常运行。但是，外接电源供电会降低部署的灵活性并增加实施成本，使用电池供电也会因容量问题限制IRS的运行寿命。为了进一步提高资源分配的灵活性，自持续IRS 辅助无线通信系统的研究引起了部分学者的兴趣[6-9]，而IRS 自持续的实现需要从射频信号中收集能量。文献[6-7]将IRS 的运行时间分为两个时隙：第1个时隙用于能量收集；第2 个时隙进行信息传输，最后通过联合优化基站（Base Station，BS）和IRS处的波束成形及两个时隙的时间调度，来最大化系统的吞吐量。文献[8-9]提出了功率分割方案维持IRS 的自持续，主要是为每个被动元件配备一个功率分割器，BS 发射信号中的一部分被反射到用户，另一部分直接通过IRS 自身进行能量收集。因此，与被动IRS 辅助的无线通信系统相比，被动IRS 自持续的实现是以牺牲系统的性能增益为代价的，并且未考虑多用户（Multi-User，MU）通信的公平性问题。

主动IRS 继承了被动IRS 的特性和硬件结构，将其中的正电阻元件替换为负电阻元件，使得主动IRS 可以同时反射和放大入射信号，进而有效地抑制双路径损耗。文献[10]中主动IRS 在有源负载的支持下，通过同时调整反射相位和幅度来放大入射信号，其研究结果表明，与被动IRS 相比，部署主动IRS 可以大幅提高系统性能。文献[11]研究了主动IRS 的自持续问题，提出了多功能IRS 的概念，即IRS 可以同时收集能量、反射和放大入射信号，来最大化用户的和速率，弥补了被动IRS 自持续辅助系统所损失的部分性能；但仍未考虑MU 通信的公平性，且主动IRS 需要更高的功耗，自持续的实现难度也会增大。

综合考虑被动IRS 和主动IRS 的优劣，学术界研究了混合智能反射面[12-14]（Hybrid IRS，HIRS），发现包含少量主动元件的HIRS 功耗较低，并且会在一定程度上抑制双路径衰减，能量效率[12]、频谱效率[13]、公平性[14]等方面均可得到显著提升。文献[12]提出了一种HIRS 架构，对一个4×2 的多输入多输出系统进行仿真。结果表明，与被动IRS 辅助的系统相比，仅含有单个主动元件的HIRS 辅助系统的能量效率提高了25%。

基于上述分析，自持续IRS 的研究集中于单纯的被动IRS 和主动IRS，并且未涉及HIRS。然而，被动IRS 自持续的研究是以牺牲系统的性能增益为代价实现的，主动IRS 的自持续模型实施难度大，且两者均未考虑MU 通信的公平性来确保每个用户的通信需求。鉴于此，本文提出了基于自持续HIRS 辅助的MU 多输入单输出（Multiple Input Single Output，MISO）下行链路通信系统的公平性传输方案。

1 系统模型与问题描述

1.1 系统模型

如图1 所示，本文考虑自持续HIRS 辅助MUMISO 下行链路通信系统，该系统模型由一个配备N根天线的BS、K个单天线用户和一个由M个反射元件组成的HIRS 构成，具体元件数量分配为M=Ma+Mp，其中Mp为被动元件个数，Ma为主动元件个数，主动元件部分记为A⊂{1,2,…,Ma}。当BS发射的线性预编码到达HIRS 时，被动元件进行能量收集以维持HIRS 的运行，主动元件通过低功率反射放大器对入射信号进行反射和放大的操作。HIRS 的系数矩阵为Θ=diag(v1,…,vM) ∈CM×M，，m∀ ∈M，其中θm∈[0,2π]和|αm|分别表示HIRS 中第m个反射元件的相移和振幅。如果m∉Λ，则此元件是被动的，振幅为|αm|∈[0,1]；如果m∈Λ，那么|αm|∈[0,amax]，amax是有源负载带来的最大功率增益，其增益可达30 dB[11]。为了便于论述分析，本文定义了一个加法分解Θ=Ψ+Φ，其中Ψ=⊙Θ表示主动元件的系数矩阵，Φ=⊙Θ表示被动元件的系数矩阵，是M×M维的对角矩阵，非零元素的位置由Λ决定且值为1，⊙是哈达玛积。

图1 系统模型

BS 发射的线性预编码信号可表示为：

式中：sk表示BS 发送给用户k的信息，满足；wk∈CN×1表示BS 发送给用户k的波束成形矢量。BS 到HIRS 的基带信道为G∈CM×N，BS 与HIRS 到第k个用户的信道分别是hd,k∈CN×1和hr,k∈CM×1。假设所有信道的信道状态信息（Channel State Information，CSI）都可以由BS 完美获得，即各链路的CSI 是理想的，用户k接收到的信号为：

HIRS 的能量收集方案设计中，被动元件将入射信号中的射频能量转换为直流功率，HIRS 收集的总功率可表示为：

由于线性能量收集模型不适用于实际电路，本文采用文献[16]中的非线性模型，故HIRS 的收集功率可表示为：

1.2 问题描述

本文的目标是在确保HIRS 自持续实现的前提下，通过联合优化BS 的发射波束成形和HIRS 的系数矩阵，最大化单个用户的最小速率，以此保证用户之间的公平性。具体的优化问题定义如下：

式中：Pmax是BS 的最大发射功率，C1 是对发射功率上界的约束，C2 是HIRS 维持自持续的功率约束条件，C3 和C4 是HIRS 系数矩阵中的振幅和相移约束。根据以上约束条件可知，P1 是一个多变量耦合且非凸的优化问题。

2 算法设计

本节采用交替优化（Alternating Optimization，AO）算法，将P1 分解为2 个子问题。利用逐次凸近 似（Successive Convex Approximations，SCA）和半正定松弛（Semi-Definite Relaxation，SDR）技术求解子问题。将P1 转换成更易处理的形式，则有：

2.1 BS 的发射波束设计

在固定HIRS 系数矩阵的条件下，优化BS 的发射波束成形wk。令，则子问题1 可写成：

约束条件C5 可以进一步细化为：

P3 中的约束条件C1 和C6 可以直接通过CVX工具解决，其余条件均为非凸，故P3 是一个难以直接求解的非凸问题。为了凸化式（11），本文引入了松弛变量{pk,qk}，可将其松弛为：

由于f(qk)=-log(1+qk)是凸函数，通过应用一阶泰勒展开式（First-Order Taylor Expansion，FTS）找到函数在任意可行点处的下界，这促使本文采用SCA 算法来解决约束条件C9。在第l次迭代时找到局部解，f(qk)的下界为：

因此，约束条件C9 可等价为：

此外，针对P3 中的功率约束条件C2，可以将主动元件消耗的功率PIRS和被动元件收集的总功率PPR改写为：

式中：Tm=diag(tm)∈CM×M，tm是第m个位置为1，其余位置为0 的M×1 维的列向量，即tm=[0,…,1,…,0]T。因此，通过引入辅助变量X和βPR，可将约束条件C2 改写为：

约束C15 左边的凸性使得约束条件为非凸，采用FTS 可近似得到第l次迭代时的可行解{X}，故X-1的下界可表示为：

一般来说，秩1 约束的求解是一个非凸问题，本文通过SDR 松弛C7 中秩为1 的约束条件，那么P3 便可以重写为一个标准凸优化问题。

式中：Γ={pk,qk,βPR,X}是辅助变量集。

因此，P4 可以直接使用CVX 工具箱[17]求解，如果秩为1，则可以通过特征值分解法获得的解，否则利用高斯随机化[18]获得P4 的近似解。

2.2 HIRS 系数矩阵设计

在获得BS 发射波束成形近似解wk*的情况下，可以通过子问题P5 优化Ψ，即：

通过FTS 展开约束C19，故其可转换为：

因此，P5 可等价为：

针对约束条件C2，同2.1 节，可将其转换为：

综上所述，P6 中的秩1 约束C26 导致其非凸，采用SDR 算法松弛秩1 约束，再通过高斯随机化求得近似解v*，对于秩为1 的解，则可以通过特征值求解。因此，最终的优化子问题可整理为：

2.3 整体算法和复杂度分析

本文所提出的目标问题是基于AO 算法求解的，算法1 总结了整体求解步骤。

对算法1 的复杂度进行分析，求解P1 问题的复杂度主要集中于第4 和第5 步。根据文献[19]，步骤4 和步骤5 的复杂度分别为

其中ε为收敛精度，D1和D2分别为求解P4 和P5中高斯随机化的次数。因此，算法1 的计算复杂度为，其中L为迭代次数。

3 仿真结果及分析

本节提供了数值结果来评估自持续HIRS 辅助MU-MISO 系统的性能。假设系统由1 个多天线的BS、1 个HIRS 和4 个单天线用户组成，其中HIRS是含有M个元件的均匀平面阵列。本文考虑仿真系统由二维平面构成，BS 和HIRS 的坐标分别为（0 m，0 m）和（50 m，10 m），4 个用户随机分布在以（100 m，0 m）为圆心、半径为5 m 的圆内。系统工作的载波频率为750 MHz，波长为λc=0.4 m[20]，大尺度衰落信道建模为L(d)=C0(d/D0)α，其中为参考距离D0=1 m 时的路径损耗，d为链路距离，α为路径损耗指数，BS-HIRS、HIRS-用户和BS-用户链路的路损指数依次为αBI=2.2，αIU=2.2 和αBU=3.6。直接链路的信道模型服从瑞利分布，级联链路和G的信道模型服从莱斯因子为5 dB 的莱斯分布，具体模型为：

除非另有规定，系统参数设置如表1 所示。

表1 仿真参数

本文所提方案是可以同时进行能量收集、信号反射和放大的HIRS 辅助的MU-MISO 通信系统。为了验证其有效性，设计了3 种基准方案。

（1）DF-IRS（Dual-Functional-IRS）辅助的通信系统。DF-IRS 是指可以同时支持能量收集和信号反射的IRS。

（2）SF-IRS（Single-Functional-IRS）辅助的通信系统。SF-IRS 是指仅反射信号的IRS。

（3）无IRS 辅助的通信系统。

图2 给出了本文方案与基准方案的最小用户速率收敛性能表现，用户速率随着迭代次数的增加而增大，并在迭代次数为15 时收敛。此外，所有基准方案的最小用户速率低于本文所提方案，说明了所提方案的有效性。

图2 迭代次数与最小用户速率的关系

图3 给出了IRS 中反射元件占比与最小用户速率之间的关系，随着信号反射元件占比的增多，DF-IRS 和本文方案的最小用户速率增加，这是因为存在更多反射元件的IRS 可以在波束成形中提供更高的灵活性，进而产生更强的级联信道。当HIRS 中的主动元件占比为0.4 时，本文方案在最小速率方面已经超过SF-IRS 基准方案。相比之下，DF-IRS的自持续成本仍然居高不下，说明了本文方案在提高用户速率和实现自持续之间的有效权衡。

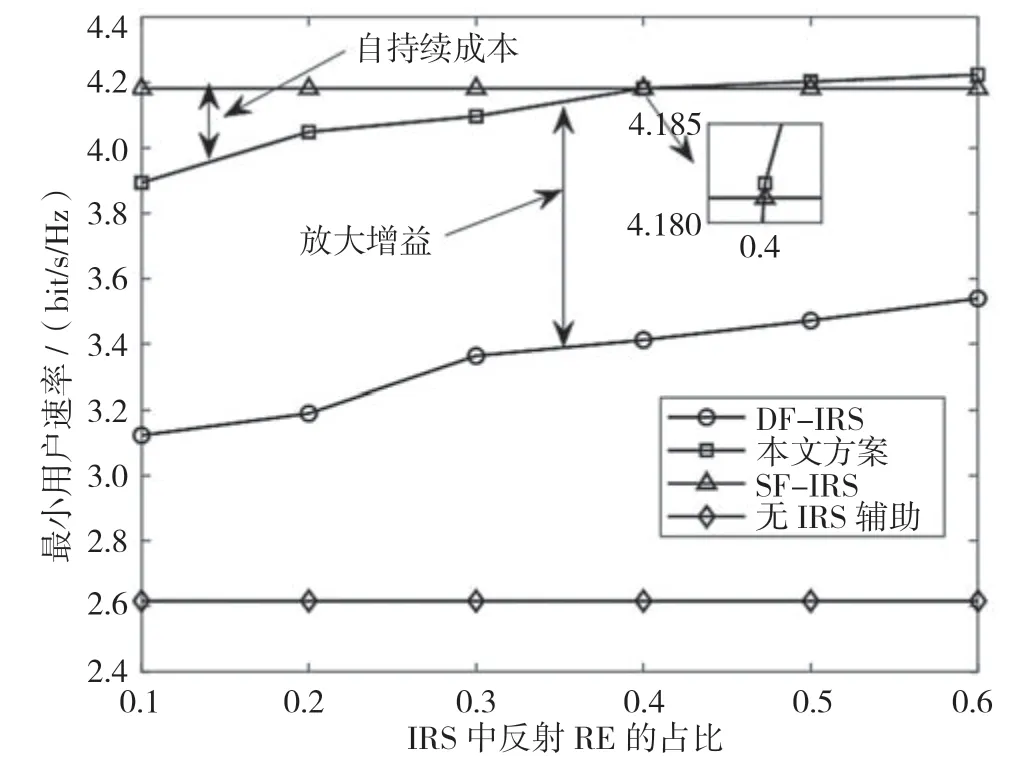
图3 IRS 中信号反射元件占比与最小用户速率的关系

图4 给出了在IRS 中信号反射元件占比为0.4的条件下，BS 发射功率与最小用户速率之间的关系曲线，可以看出本文所提方案优于基准方案，但是与SF-IRS 方案之间的差距较小，主要原因是SFIRS 理想化地忽略自身的能量消耗。而本文充分考虑到能耗问题，提出了HIRS 的自持续方案，以保证HIRS 在没有外供电的情况下正常运行。随着BS发射功率的增大，两者之间的差距也增大。相较于无IRS 辅助的方案，有IRS 可以为系统提供额外的级联链路，所提方案与无IRS 辅助方案之间的性能差距逐渐变大。

图4 BS 发射功率与最小用户速率的关系

图5 给出了BS 天线数量与最小用户速率之间的关系，两者是正相关的。这是因为BS 的天线数量越多，可以获得的波束成形增益越大，从而增大信号的传输速率。对比不同尺寸大小的HIRS 可以看出，随着元件数量M的增多，本文所提方案的最小用户速率也随之增大。原因在于，HIRS 可以增强级联链路的信道增益。

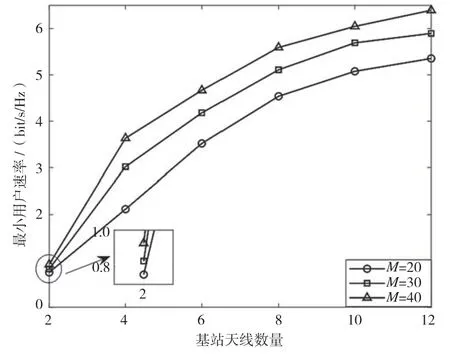
图5 BS 天线数量与最小用户速率的关系

4 结语

本文提出了自持续HIRS 辅助的MU-MISO 下行链路通信系统，集信号反射、信号放大和能量收集于一体的HIRS 可以在维持自持续的前提下，最大化最小用户速率，实现MU 通信的公平性。通过考虑BS 发射波束成形和HIRS 系数矩阵的耦合，建立了最大化最小用户速率的非凸优化问题。为此，设计了高效的AO 算法，将原始目标问题分解为2个单变量的子问题，利用SCA和SDR技术进行求解。仿真结果表明，本文所提方案优于基准方案，且与SF-IRS 方案相比，选择适当数量的主动元件便于有效地平衡用户速率提高和IRS 自持续实现之间的关系。