基于深度学习节点表示的谣言源定位方法*
2024-03-19罗佳莉王赛威
刘 维,杨 洁,罗佳莉,王赛威,陈 崚
(扬州大学信息工程学院,江苏 扬州 225000)
1 引言
近年来,社交媒体的普及使得谣言迅速传播,这对社会稳定和政府公信力构成了一定的威胁。虚假信息混入公共事件,不仅可能引起公众的恐慌,还可能给公众带来伤害[1]。此外,虚假新闻也可能会损害企业和个人的声誉。谣言会误导人们的思想,导致他们对某些问题产生误解进而做出错误的决定。以全球抗击COVID-19疫情为例,一些人故意散布饮用烈酒可以杀死病毒的谣言。有人相信了这一谣言,开始大量饮酒而未采取科学的预防措施。这样的谣言不仅妨碍了疫情防控工作的开展,还对国家的经济发展产生了不利的影响。
为了控制谣言的传播范围,定位谣言源至关重要。在实际应用中,我们虽然不知道谣言的具体来源,但是可以通过找到一些受到谣言影响的观测节点并根据观测节点的信息来定位谣言源。Shah等人[2]首次提出了谣言源定位问题。他们把这一问题定义为:给出一组受谣言影响的观测节点O和其被影响的时间T,谣言源定位的目的是识别一个由k个谣言源组成的节点集S,使其影响范围I(S)能够最大限度地覆盖O中的观测节点。同时,要保证谣言源到O中观测节点的距离与它们的影响时间T高度一致。
近年来,很多学者对这个问题进行了研究。有些学者从网络拓扑结构角度出发,假设谣言源与节点的中心性有关并据此展开了研究。例如,文献[2-4]利用不同的中心性测量方法定位源节点。然而,由于基于中心性的方法忽略了观测的节点信息和边上的传播概率,这些方法对谣言源的定位效果并不理想。还有一些研究[5,6]将扩散图构建为生成树,将生成树的根作为源节点进行谣言定位。然而,由于树结构只是原始网络的一个子图,基于树结构的方法并不能准确反映原始网络中的影响力传播。此外,所有这些研究都假设网络中只有一个谣言源,然而现实世界中谣言源往往不止一个,因此许多学者开始将研究重心转移到多谣言源定位问题上来。
多谣言源定位方法主要可以分为3类:基于社区的多谣言源定位方法、基于传播路径的多谣言源定位方法和基于排名的多谣言源定位方法。基于社区的多谣言源定位方法[7,8]首先利用网络的拓扑信息对网络进行划分,然后在每个社区内解决单源识别问题。然而,基于社区的多谣言源定位方法的效果在很大程度上取决于观测节点的选择。基于传播路径的方法从反向传播[9]、贝叶斯理论[10]、感染序列[11]和置信集[12]等角度考虑来自每个谣言源节点的复杂感染路径。然而,这些多谣言源检测方法大多采用贪婪的策略来寻找谣言源,因此需要多次模拟来估计每个候选源节点集的传播范围。由于这2类方法时间复杂度较高,所以并不适用于大规模网络。基于排名的多谣言源定位方法[10,12]首先估计一些度量值,用这些度量值表示节点作为源的概率,然后根据度量值对节点进行排序,最后选择度量值最高的节点作为源节点。然而,这些方法认为网络中的所有节点和边都是相同的,忽略了信息传播中观测到的节点的关键潜在拓扑特征。由于节点的关键拓扑特征丢失,这些方法谣言源定位的效果往往不够理想。
为了充分考虑谣言以及扩散过程中各个特征之间的关联性,减少因路径分析造成的大量计算,本文提出一种基于深度学习的谣言源定位方法。该方法首先从节点的扩散路径角度定义所有节点与观测节点之间的路径相似度,从节点的传播时间角度定义节点的影响力向量,从节点之间关系的角度定义节点与其他节点的影响力相似度。其次,本文设计一个包含编码解码模块的自编码神经网络对节点的影响力向量进行编码。需要特别关注的是,在网络的训练过程中,本文使用节点的路径相似度以及节点的影响力相似度对训练过程加以限制,最终得到包含了扩散路径、传播时间和节点信息的新的节点嵌入表示。最后,根据得到的节点嵌入表示计算节点为源的概率,从而实现谣言源的定位。
本文的主要工作如下:
(1) 提出一种基于随机游走计算节点与观测节点之间相似度的算法。
(2) 考虑观测节点的感染时间,提出一种节点表示来度量每个节点与估计源之间的距离。
(3) 结合节点感染时间和节点与观测节点的相似度,设计节点编码方法。
(4) 通过整合节点的拓扑特征及其与网络中观察节点的距离,提出一种基于深度学习的方法。该方法能有效、准确地识别影响源且能适用于多种传播模型。
(5) 在4个真实网络和2个合成网络上的实验结果表明,该方法在谣言源定位方面具有优势,并且可以在更短的时间内获得比其他方法更高的效率。
2 相关工作
最早的单谣言源定位方法大多关注网络的拓扑结构,依赖节点的中心性信息定位谣言源。Shah等人[2]首先定义了谣言源定位问题,并提出了“谣言中心性”来定位谣言源。Zhu等人[13]利用节点的“偏心率”,即一个候选源到其可到达的最远节点的最大距离,来估计网络中的真实源。Jog等人[14]研究了随机生长树中的节点中心性,提出了质量中心的概念并给出了中心性的下限。Kouzy等人[15]提出了一种使用社区结构中桥节点来定位谣言源的方法。然而,这些基于中心性的方法大多使用树结构来检测谣言源,将一般的图改造成生成树,或者只是在树和树状子图上估计原始传播源。由于树结构只是原始网络的一个子图,基于树状结构的方法不能准确反映原始网络中的谣言真实传播。由于基于中心性的方法的表现很大程度上依赖于源节点在网络中的位置,只有当谣言源节点相对靠近图的中心时,这些方法的表现才会比较好。因此,这些方法不能很好地适用于现实情况。
为了缩小谣言源的搜索范围,许多研究人员试图利用观测到的节点信息定位谣言源。基于感染网络的理论基础,一些研究人员通过在社交网络中部署传感器和观测者的方式获得更多关于谣言传播过程的信息。基于观测到的节点信息,Hu等人[16]基于反向传播和整数规划修改了谣言源定位的最大最小值方法,通过结合节点的传播延迟和0-1整数规划来定位谣言源。然而,所提方法仅考虑传播延迟和扩散时间是不足以准确定位源节点的,因为传播路径信息也非常重要。基于传播路径分析,Zhu等人[17]将谣言源定位问题转化为观测节点的信息排序问题。他们根据受感染节点影响的节点的概率和被感染的成本来定位谣言源。作者没有具体说明观测节点的选择,但是该方法中时间戳的推导完全基于观测节点,因此如何选择观测节点与他们提出的方法高度相关。
在现实世界的社交网络中,错误信息来源于多个谣言源,通过如Twitter、Sina和其他社交网络等多种不同的渠道进行传播。模拟不同来源谣言的传播和从观测节点记录的信息中找到这些传播源是至关重要的。现有的多谣言源定位方法主要分为3类:基于社区划分的多谣言定位方法、基于传播路径的多谣言源定位方法和基于排名的多谣言定位方法。基于社区划分的方法首先将网络划分为多个社区,然后在每个社区中找到传播源。Nguyen等人[9]通过网络聚类设计了一种基于独立级联模型的启发式算法,通过反向扩散确定多个候选源节点。然而,该算法仅依靠节点的状态来检测谣言源,没有充分考虑可能的感染信息。基于反向传播和分而治之的方法,Zang等人[5]提出了基于SIR(Susceptible Infected Recovered)模型的多谣言源定位问题。他们提出了一种社区检测方法,将恢复的节点划分到多个感染社区,然后用最大似然法定位每个社区的感染源。然而,作者直接使用了已有的社区检测算法,没有根据感染信息划分社区,因此不能很好地解决谣言源定位问题。Khim等人[18]分析了感染子图,并使用置信集估计源节点的数量,但是这种方法只适用于常规树状网络。Ding等人[7]提出了一种基于有效距离的网络划分方法,将多谣言源定位问题转化为单谣言源定位问题。然而,他们并没有研究使用不同的有效距离对谣言源定位问题的影响。Li等人[19]提出了一种基于路径的多路网络源定位方法。该方法基于源中心性理论,采用标签迭代过程寻找局部标签最大的节点作为源。考虑到感染子图的结构和谣言传播的随机性,Qiu等人[20]提出了一种基于时间戳反向传播的估计方法定位谣言源。基于排名的多谣言源定位方法首先定义和估计一些代表节点作为谣言源的概率,然后根据这些值对节点进行排名。Zhang等人[10]使用贝叶斯反追踪模型提出激活原因的后验概率,并选择随机游走命中率高的节点作为谣言源。然而,该方法需要大量的计算,所以不适用于大规模网络。Dawkins等人[12]定义了多谣言源定位的置信集,根据置信集,他们提出了2种节点抽样方法来构建候选谣言源集合。
有些方法将单谣言源定位问题转化为一个分类问题,并使用基于神经网络的学习方法来识别谣言源。例如,文献[12,21]分别是基于图神经网络GNN(Graph Neural Network)和门循环单元GRU(Gate Recurrent Unit)的单谣言源神经网络方法。但是,这些方法都只是根据网络的拓扑信息建立目标函数,忽略了观测节点被感染的时间信息。观测节点的受影响时间是谣言源定位的重要信息,因此忽略受影响时间的方法不能满足特征提取的训练要求,也不能获得高精度的结果。
3 预备知识
本节介绍独立级联模型,并定义多谣言源定位问题。
3.1 独立级联模型
本文对独立级联IC(Independent Cascade)传播模型下的多个谣言源定位问题进行研究。独立级联模型是社交网络中常用的信息传播模型之一。在这个模型下,信息传播过程中任意时刻每个节点都处于2种状态之一:激活状态或未激活状态。初始状态下,所有的源节点都是激活状态,其它节点处于未激活状态。传播开始时,源节点尝试去激活它的邻居节点,如果邻居节点被激活,那么被激活的节点会在下一个时刻继续激活它的邻居节点。节点是否能激活邻居节点,与其它节点的激活结果无关。此外,该模型假设每个被激活的节点有且仅有一次机会激活其邻居节点。无论成功与否,都不会再有机会激活其邻居节点。当没有新的节点可以被激活时,信息传播过程就结束了。源节点的影响范围就是最终受影响的节点集合。

Figure 1 Framework of the proposed method图1 本文所提方法框架
3.2 多谣言源定位问题
社交网络可以用图G=(V,E,P)的形式描述,其中,V表示节点集合,|V|=N,E表示边集,P=[pu,v]表示边的权重矩阵。对于每一条边(u,v)∈E,pu,v∈(0,1)是节点u到它的邻居节点v的传播概率。O={o1,…,om,…,oM}表示随机从节点集合V中选取的观测节点集合,M<|V|。T={t1,…,tm,…,tM}表示观测节点被影响的时间集合。
定义1(谣言源的影响范围) 设社交网络为G=(V,E,P),S⊆V为谣言源在IC模型下从t=0时刻开始传播影响的所有节点集合。各个谣言源之间的传播是相互独立的,在足够长的时间T后传播终止。谣言源的影响范围I(S)表示被源节点集合S在时间T后激活的节点集合。
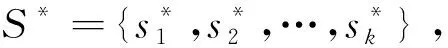
在现实世界中,观测节点集合O的选择必须满足以下条件:对于任意2个节点v1和v2,至少存在O中的一个节点o使得该节点分别到v1和v2的距离不相同。基于上述条件,本文选择一个双重可分解集[22]作为观测节点集。
3.3 方法框架
图1描述了本文在IC模型下定位多个谣言源方法的框架。本文所提方法首先根据观测节点被影响的时间和节点与观测节点之间的距离定义节点的影响力向量。然后,设计一个自动编码AE(Auto Encoder)神经网络对节点的影响力向量进行编码。在模型训练的过程中,加入路径信息和节点信息对模型进行约束。通过神经网络的训练得到包含了谣言扩散路径、传播时间和节点信息的节点嵌入表示。最后,通过节点的嵌入表示计算节点为谣言源的概率并选择概率最高的节点为源节点,实现谣言源的定位。

4 基于深度学习的节点表示
本节提出一个自动编码器(AE)网络,它将节点嵌入到一个反映谣言的扩散路径、传播时间和节点的邻居信息的潜在空间。首先,提出一种基于随机游走的路径分析算法,根据每一个节点与观测节点的可能路径,从节点与观测节点的受影响状态获得节点表征。然后,将节点表征输入AE网络,得到每个节点的嵌入表示输出。该嵌入表示反映了节点在潜在空间中的扩散路径、传播时间和节点信息。
4.1 基于随机游走的路径分析算法
假设在t1=0,q(R≥q≥1)时刻谣言源开始传播谣言,其中R为谣言传播时间上限。在传播过程中,一些随机选择的观测节点会记录下它们被影响的时间T。
为了估计谣言源节点对被观测节点的传播范围,本文定义随机可达路径,以确定影响观测节点的候选源节点。在现实生活中,谣言的传播没有闭环,而且长度小于Q,定义H(H≤Q)为传播路径长度的最大值。
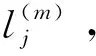

定义5(路径相似性) 假设从观测节点om开始有K条随机可达路径,则观测节点om与节点v之间的路径相似性可定义为式(1)所示:
(1)
上述路径相似性反映了这2个节点被同一个谣言源影响的可能性。连接它们的随机可达路径越多,它们的路径相似度越高。因此,路径相似性αm,v反映了谣言在传播过程中传播路径的属性。

(2)

(3)

定义7(影响力相似度) 根据影响力向量的定义,2个节点u和v的相似性定义为式(4)所示:
(4)
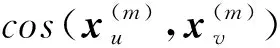
(5)
节点u和节点v到同一观测节点的随机可达路径越多,它们的相似度就越高。也就是说,节点之间的影响力相似度ru,v越高,说明它们在潜在空间的距离应该更近。因此,节点之间的影响力相似度反映了节点的信息。
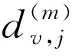

Figure 2 Structure of auto-encoder network图2 自编码神经网络结构
设|V|=N,算法1的时间复杂度为O(M×K×H)。由于M和K为常数且H≤N,所以算法1的时间复杂度为O(N)。

算法1 RW-Path-Analysis算法输入:G':G=(V,E,P)的逆向图;H:随机游走路径的最大长度;K:采样次数;O:观测节点集合。输出:l:所有随机游走路径集合,对于观测节点om,lm={l(m)1,l(m)2,…,l(m)j,…,l(m)K},其中l(m)j是从om开始的第j条随机游走路径;Cm:观测节点om的候选源节点集合;d(m)v,j:om和v的随机可达路径l(m)j长度;αm,v:om和v的路径相似度。1.BEGIN2. FOR m∈[1,M]DO3. FORj∈[1,K]DO4. u←om;l(m)j={om};d(m)v,j=+∞;5. FORh∈[1,H]DO6. 根据概率pw,u选择G'中节点u的一个邻居节点w;7. lmj=lmj∪{w}; Cm∪{w};8. d(m)v,j=h;αm,w=αm,w+1K;9. u←w;10. END11. END12. END13. RETURNl,C,d=d(m)v,j M×N, A=αm,v M×N14.END

4.2 自编码神经网络
本文提出一个自编码(AE)网络,该网络将节点的影响力向量作为输入,以节点与观测节点之间的路径相似度和节点之间的影响力相似度作为约束,训练得到包含节点信息、传播路径信息和传播时间的节点嵌入表示。


4.3 激活函数

(6)
其中,w(m)1和b(m)1表示权重和偏差,σ(·)表示激活函数。本文使用tanh作为激活函数,如式(7)所示:
(7)
那么第l′层输出的节点v与观测节点om有关的中间嵌入向量如式(8)所示:
(8)
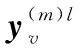
(9)
(10)
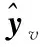
(11)
(12)
(13)
(14)

4.4 损失函数

(15)

其次,本文使用损失Lossα保证节点嵌入zv保留了节点v与其它节点之间的传播路径信息,Lossα的计算如式(16)所示:
(16)
其中,αu,v为节点u与节点v之间的路径相似度。Lossx的加入使得路径相似度接近的节点嵌入在潜在空间的距离更近,这就保证了在训练过程中节点嵌入zv很好地保留了谣言源定位需要的传播路径信息。
此外,本文使用损失Lossr保证节点嵌入zv保留了节点v与其他节点之间的信息,如式(17)所示:
(17)
其中,ru,v为节点u与节点v之间的节点相似度。损失Lossr的加入保证了神经网络训练时保留了节点信息,也就是说相似的节点在潜在空间的嵌入更接近。
定义正则化项Lossreg如式(18)所示:
(18)
基于上述损失项,定义自编码网络的损失函数如式(19)所示:
Loss=Lossx+αLossα+βLossr+γLossreg
(19)
该损失函数保证了自编码网络将节点向量映射到了一个包含传播路径、传播时间和节点信息的潜在空间。
4.5 自编码网络的训练
为了训练自编码网络,本文采用随机梯度下降SGD(Stochastic Gradient Descent)法最小化式(19)定义的损失。

Lossα=2tr(ZTL(α)Z)
(20)
Lossr=2tr(ZTL(r)Z)
(21)
其中,tr(·)是矩阵的迹,Z是节点的嵌入向量。
为了训练自编码网络,本文使用随机梯度下降法通过更新每一个参数θ最小化损失函数,如式(22)所示:
(22)


(23)
(24)
(25)
(26)
通过随机梯度下降法,式(22)以反向传播的方式更新参数,使损失函数最小。这个嵌入计算和参数更新的过程不断重复,直到收敛。训练AE网络的算法如算法2所示。

算法2 训练自编码网络输入:节点v与观测节点之间的影响力向量x(1)v,…,x(M)v;A:路径相似度矩阵;O:观测节点集合;α,β,γ,ε:参数;e:迭代次数。输出:节点v的影响力向量zv。1.BEGIN2. initialize w,b,^w,^b3. WHILE the difference of the loss values between two consecutive iterations is less than εDO4. Compute the embedding zv and restored vector ^x(m)v according to Eq. (6) through Eq. (14);5. ComputeLoss according to Eq. (19);6. Updatew,b,^w,^b according to Eq. (22) through Eq. (26) using SGD;7. END8. RETURNzv9.END
5 基于深度学习的谣言源定位
5.1 基于随机游走的路径分析方法
本文通过自编码网络得到了节点的嵌入zv,那么每个节点v为观测节点om的谣言源的概率如式(27)所示:
(27)
而节点v是观测节点集合O中的谣言源的概率可以通过式(28)计算:
(28)
本文选择概率P(O|v)最高的节点为谣言源。基于深度学习的谣言源定位方法DL-SIA的伪代码如算法3所示。

算法3 基于深度学习的谣言源定位方法(DL-SIA)输入:G=(V,E,P):社交网络;k:谣言源的数量;O:观测节点集合;T:观测节点的感染时间。输出:S*={S*1,S*2,…,S*k}:谣言源节点集合。1.BEGIN2. RW-Path-Analysis;/*get Cm and A by Algorithm 1*/3. Compute the influence vector x(m)v by Eq. (2) and Eq.(3);4. Compute the influence similarity matrix R=[ru,v] by Eq. (4);5. Train the AE network and output the embedding z by calling Algorithm 2;6. Estimate the likelihood P(O|v) of all the nodes ac-cording to Eq. (28);7. Choose the k nodes with the maximal likelihoods as the sources S*={S*1,S*2,…,S*k};8. RETURN S*9.END
5.2 复杂度分析
设N为边集V中的节点数,K为随机可达路径数,H为随机可达路径长度。计算路径相似度的时间复杂度为O(H×K×N)。由于计算影响力向量需要遍历所有的观测者和节点,其计算复杂度为O(M×N),其中M为观测到的节点数。在AE网络中,编码器和解码器部分的层数都是L。因此,DL-SIA的总复杂度为O(N·(H×K+M+(2L+1)·H))。在最坏的情况下,所有被感染的节点都被选为观测者,即M=N。因为K、L和H都可以被视为常数,因此DL-SIA的时间复杂度为O(2N2)。
6 实验设计
6.1 数据集
在2个虚拟网络BA和WS,4个真实网络Email-Eu-core[23],ego-Facebook[24]USpowergrid[25]和wiki-vote[26]上评估了本文方法。
表1列出了6个网络的拓扑结构属性。其中,网络直径指的是网络中最长最短路径的长度。平均聚类系数用于衡量节点与其邻居节点之间联系的紧密程度。网络的平均路径长度NL定义为任意2个节点vi和vj之间距离dij的平均值,如式(29)所示:
(29)
其中,N为节点数。
表2列出了DL-SIA方法在不同网络上的神经网络参数设置。

Table 1 Topological features of the networks表1 不同网络的拓扑结构

Table 2 Default settings of neural networks in different datasets表2 不同网络集上的神经网络设置
6.2 对比方法
为了验证提出的DL-SIA方法的有效性,本文将其与多种方法进行对比。对于单谣言源检测问题,本文将DL-SIA与谣言中心性RC(Rumour Centrality)[2]、约旦中心性JC(Jordan Centrality)[13]、EPA(Exoneration and Prominence based Age)方法[27]和DMP(Dynamic Message Passing)方法[28]进行比较。对于多谣言源检测问题,本文将DL-SIA与NETSLEUTH[29]和K-Center[30]方法进行对比。
6.3 评估指标
本文采用平均错误距离AED(Average Error Distance)和准确率(Precision)2个评价指标来衡量谣言源定位方法的有效性。
(1)平均错误距离。

(30)

(2)准确率。

(31)
准确率越高说明方法的效果越好。
7 结果
7.1 参数对DL-SIA方法的影响
本文在不同的参数设置下分别做了实验。α、β和γ为控制损失函数中各个项之间重要性的3个参数。τ为控制观测节点om的感染时间与其它节点之间距离差异的参数,per为观测节点的数量在所有节点数量中的占比。
7.1.1α、β和γ对实验结果的影响
本文测试控制损失函数的3个参数α、β和γ对实验结果的影响。图3展示了不同参数对损失函数值的影响。从图3可以看出,对于不同的网络,节点v和被观测节点om的表示与Loss中的Lossα并不是强关联的。图3的等高线色谱图证明了这一结论。从图3中可以看出,α和β的取值对神经网络的损失影响不大。此外,从三维图中可以看出,α的值应在0.5~0.6,以获得快速收敛。

Figure 3 Effect of α and β on loss function图3 损失函数中α、β的影响
与损失函数对参数α的不敏感相比,损失函数对β的值更为敏感,该值代表了节点和观测节点之间相互关系的影响。这一结果也与现实生活中的影响力传播过程高度一致,即受影响时间与到源节点的距离之差越小,值越高。不同网络α和β的最佳值是不同的,但大多数测试结果表明,α和β最佳值集中在0.5 ~ 0.7。
本文还测试了正则项参数γ对损失函数的影响。图4展示了在ego-Facebook网络上损失的变化趋势。从图4中可以看出,不同的γ值损失函数值变化不大,其中图4a为100次迭代损失的总体变化趋势,图4b为第50次~第100次迭代损失的总体变化趋势。在对每个网络进行测试期间,将迭代次数设置为接近于0的值。在本文的实验中,根据迭代次数将γ设置在0.5以内。

Figure 4 The loss function under different values of γ图4 损失函数中γ的影响
7.1.2 衰减因子
衰减因子调整了观测节点被影响时间和节点距离差异的重要性。本文测试了DL-SIA在不同的衰减因子下的平均错误距离。图5展示了利用DL-SIA方法在真实网络上进行谣言源检测的平均错误距离。图5中的结果显示,当参数在[0.42,0.53]取值时,DL-SIA方法的平均错误距离越低,说明在此范围内谣言源定位的效果越好。

Figure 5 AED under different values of τ图5 衰减因子τ对实验结果的影响
7.1.3 观测节点占比以及随机可达路径的长度
实验中为了避免多个节点与任何观测节点有相同距离的情况,本文选择了一个双可解集作为观测节点集合。本文测试了Dl-SIA方法在不同的观测节点占比以及不同的路径长度下的表现。图6展示了在不同的观测节点占比和不同路径长度下方法的平均错误距离。图中横轴代表观测节点占比,纵轴代表路径长度,每个网格的颜色代表其在设定的坐标参数下实验得到的平均错误距离,颜色越深代表平均错误距离越长。
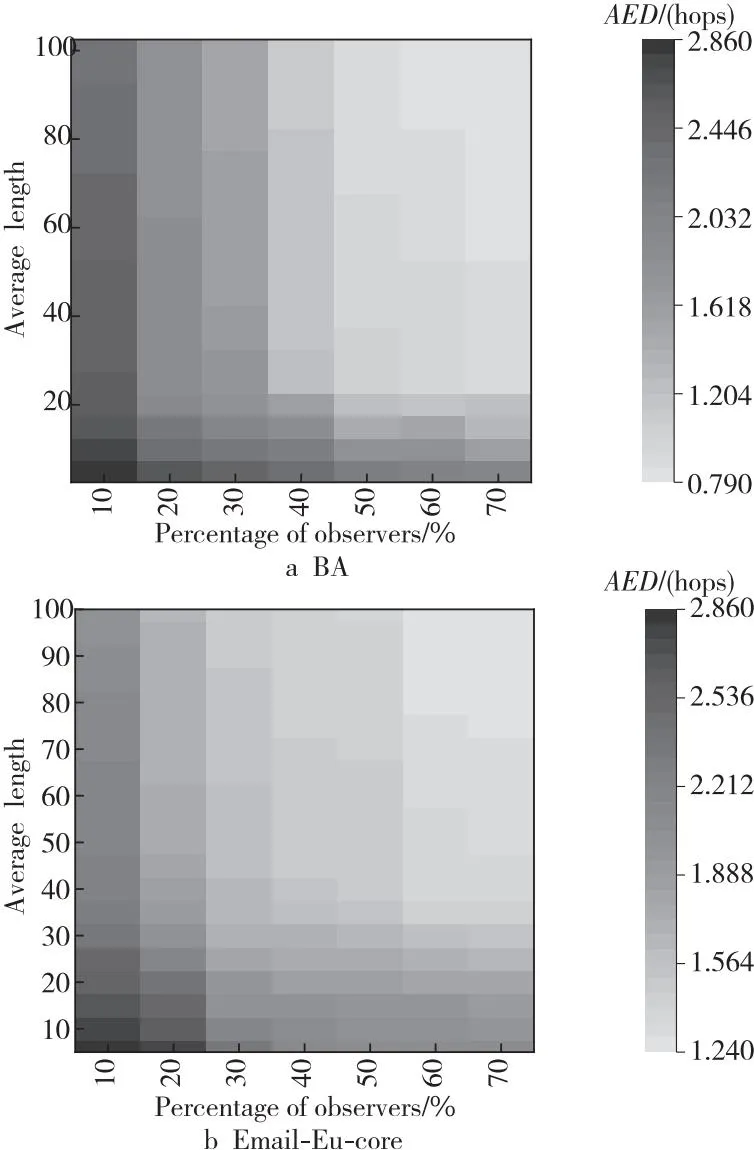
Figure 6 AED of different percentages of observers and the average length of randomly reachable paths图6 不同比例观测节点和不同的 随机路径长度对实验结果的影响
从图6可以看出,当路径长度增加时,本文方法的效果提升越明显。由于计算量随路径长度线性增加,运行时间也以可接受的速度增加。这一结果也表明,融合深度学习框架可以获得更高的效率,并保持相对好的谣言源定位效果。由于真实网络的连接性比虚拟网络更强,平均路径长度越长,平均聚类系数越高,上述现象在真实网络中更为明显。当检测到的平均路径长度达到20时,本文方法的准确性明显提高,平均误差距离下降到2跳左右。然而,当路径长度超过20时,这种改善相对较小。可以为每个网络设置一个合适的路径长度,尽可能减少计算时间,以保证本文方法能达到理想的效果。
从图6可以看出,在观测节点占比较小时,观测节点占比的增加对DL-SIA方法效果的影响较小。然而,当观测节点的占比达到大约30%~40%时,DL-SIA的平均错误距离会明显下降。这一结果表明,观测节点的占比对DL-SIA的效果有着较大的影响。因此,考虑到实际环境和计算成本并保证DL-SIA的效果,本文得出以下结论:观测节点的占比应该在40%~60%,随机路径长度应该在30~50。上述参数可以根据网络规模适当调整。
7.2 消融实验
为了进一步证明本文方法DL-SIA的有效性,设计了消融实验。由于Lossreg是自编码网络中的一个正则项,本文考虑以下4种情况并进行实验:
情况1将Lossx+Lossreg作为损失函数,即自编码网络使用节点的影响力向量作为节点的初始特征输入神经网络,不使用路径相似性及节点相似性信息对训练过程加以限制。
情况2将Lossx+Lossreg+Lossα作为损失函数,即自编码网络使用节点的影响力向量作为节点的初始特征输入神经网络,并使用路径相似性限制训练过程。最终通过自编码网络得到的节点嵌入表示同时包含传播时间信息及传播的路径信息。
情况3将Lossx+Lossreg+Lossr作为损失函数,即自编码网络使用节点的影响力向量作为节点的初始特征输入神经网络,并使用节点相似性限制训练过程,最终得到包含节点信息和传播时间的节点嵌入表示。
情况4使用DL-SIA方法损失函数,即Lossx+αLossα+βLossr+γLossreg。自编码网络将节点的影响力向量作为输入,并利用路径相似性及节点相似性将节点映射到包含传播时间、传播路径及节点信息的潜在空间,得到新的节点嵌入表示。
表3为上述4种情况得到的准确率和平均错误距离。可以看到,情况1只使用Lossx作为损失函数时得到的结果最差。对于情况2,准确率提高了5.30%,平均错误距离降低了7.78%。对于情况3,平均精度提高了5.30%,平均错误距离降低了23.51%。这表明,在训练过程中加入路径相似性以及节点相似性信息有助于提高谣言源检测的精度。此外,据观察,加入Lossr对于提高DL-SIA方法的性能比加入Lossα更为突出。
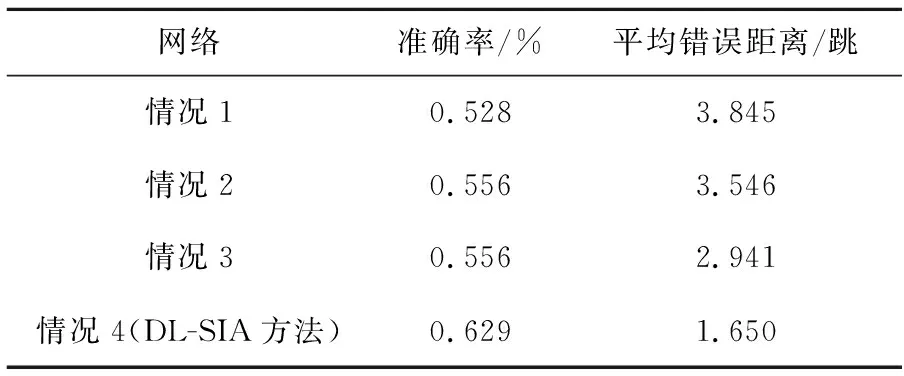
Table 3 Precision and average error distance in four different situations表3 4种情况下方法的准确率和平均错误距离
对于情况4,由于损失函数同时包含Lossα和Lossr,所以DL-SIA方法的精度得到了很大的提高。与情况1中使用的基本损失函数相比,当使用DL-SIA方法的损失函数时,平均精度提高了19.13%,平均错误距离降低了57.09%。上述消融实验结果充分证明了DL-SIA方法设计是合理有效的。
7.3 谣言源定位的准确率
图7展示了所有方法在每个网络上的准确率。从图7可以看出,本文DL-SIA方法优于其他基于中心性和基于感染路径的方法。DL-SIA在BA、WS、Email-Eu-core和ego-Facebook网络中的准确率明显提高了25.0%~41.8%。从这4个网络的准确率趋势变化可以看出,当观测节点的占比超过40%时,谣言源定位效果的提升就会放缓。总的来说,DL-SIA方法的准确率远远高于其他方法的,这表明DL-SIA方法的谣言源定位能力很强。此外,随着观测节点占比的增加,DL-SIA方法准确率也随之提高,这也表明了DL-SIA方法设计中节点信息嵌入的科学性和准确性。
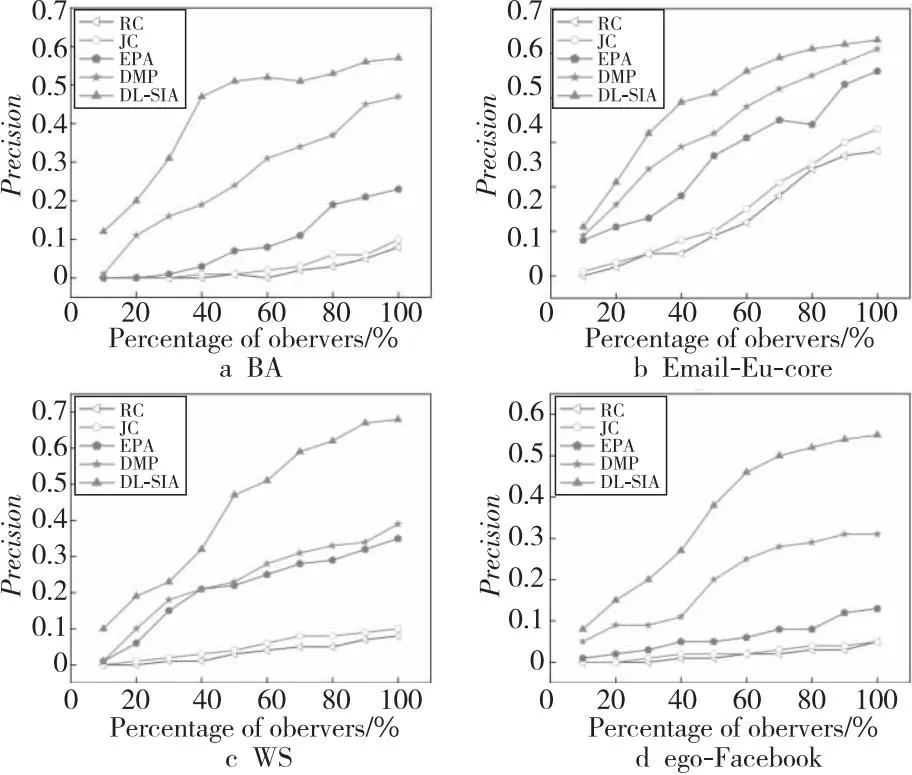
Figure 7 Precision values of different methods图7 不同方法的准确率
7.4 谣言源定位的平均错误距离
为了验证本文DL-SIA方法的准确性,还测试了其平均错误距离,并将其和其他方法的平均错误距离进行了比较。
图8展示了各方法在2个模拟网络(BA,WS)和2个真实网络(Email-Eu-core,ego-Facebook)上的平均错误距离。与RC和JC等中心性方法相比,DL-SIA方法的平均错误距离较小。以1 000节点规模的网络为例,如BA、WS和Email-Eu-core,在观测节点占比较低的情况下,DL-SIA取得的平均错误距离相比其他方法的要低得多。这一结果表明,DL-SIA方法真实谣言源和估计谣言源之间的距离比其它方法的少约2.18跳。在大规模网络ego-Facebook的测试中,与其他方法相比,DL-SIA定位到源节点的平均错误距离比真实谣言源减少了约4.82跳。这一结果表明,在更大规模的网络中,DL-SIA方法相对其他对比方法表现更出色。在定位的初始阶段,DL-SIA的平均错误距离与DMP方法的接近,但DMP方法的优势并不明显。从整体情况来看,与DL-SIA方法相比,DMP方法在早期阶段获得的微小优势不能掩盖其整体效果的不足。

Figure 8 Average error distances of different methods图8 不同方法的平均错误距离
图9~图12展示了这4个网络上不同数量谣言源的平均错误距离分布。本文将DL-SIA的平均错误距离与Net Sleuth和K-Center方法的平均错误距离进行了比较。如图9~图12所示,当随机选择2个谣言源时,Net Sleuth、K-Center和DL-SIA取得了相似的性能。但是,通过观察直方图的峰值可以发现,DL-SIA的平均错误距离集中在大约0~2跳,而K-Center在1~3跳,Net Sleuth在2~5跳。
表4展示了本文提出的多谣言源定位方法的平均错误距离。表4中的比例指的是由各方法得出的源节点与实际源节点的距离不超过3跳的概率。从表4可以看出,当谣言源数设置为2和3时,K-Center的平均错误距离与DL-SIA的接近。与K-Center方法相比,DL-SIA方法的平均错误距离可以减少约7.9%~19.5%。实验中,Net Sleuth的结果最差。
随着谣言源节点数量的增加,DL-SIA的平均错误距离稳定在3跳。从表4可以看出,尽管网络中存在多个源,但DL-SIA方法的平均错误距离与其他方法的相比,有22.9%~38.8%的改善。这一统计结果表明,DL-SIA可以处理网络中多谣言源传播的复杂情况。而随着源节点数量的增加,DL-SIA的表现更加突出,在平均错误距离上获得了近50%的改进。

Figure 9 Average error distances of different methods when k=2图9 不同方法在k=2时的平均错误距离

Figure 10 Average error distances of different methods when k=3图10 不同方法在k=3时的平均错误距离
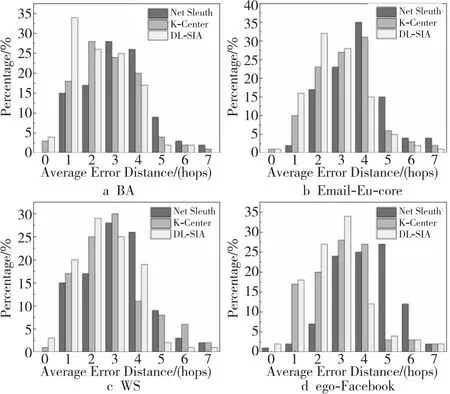
Figure 11 Average error distances of different methods when k=4图11 不同方法在k=4时的平均错误距离

Figure 12 Average error distances of different methods when k=5图12 不同方法在k=5时的平均错误距离
7.5 运行时间
图13展示了不同观测节点占比下DL-SIA单源检测的计算时间。从图13中可以看出,计算时间随着观测节点数量的增加呈线性增加。这一结果也证明了结合深度学习框架的谣言源定位方法可以获得更高的效率,并保持相对较高的精度。
本文测试了DL-SIA方法在不同占比的观测节点和不同路径长度下在4个网络上的运行时间。将观测到的节点占比设定为40%,路径长度设定为40。
图14为不同方法的运行时间测试结果,在大多数情况下,DL-SIA方法的运行速度要比DMP和EDA的快。RC和JC的计算时间低于其他方法的。基于中心性的方法RC和JC的计算时间较短,这是因为它们的计算只考虑每个节点的中心度。其他3种方法需要根据网络的全局拓扑信息计算每个节点在每个时间步的状态。但是,基于中心性的方法RC和JC的准确率要比DL-SIA方法的低得多,因为它们为了速度牺牲了准确率。综合考虑实验的效果和运行时间,本文的DL-ISA方法相比其他方法有着更优秀的表现。对于DMP和EPA方法,尽管DMP相比EPA有更高的准确率,但它需要2倍多的时间来获得与EPA相同的准确率。特别是在一些大规模的网络中,DMP甚至无法准确定位谣言源。
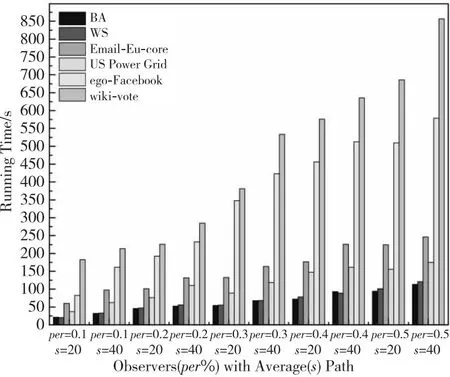
Figure 13 Running time of DL-SIA under different percentages of observers and path length图13 DL-SIA方法在不同比例观测者 和随机可达路径长度下的运行时间

Figure 14 Running time of different methods图14 不同方法的运行时间
8 结束语
本文提出了一种名为DL-SIA的基于深度学习的方法,该方法可以整合谣言的扩散时间、传播路径以及节点的拓扑特征信息来定位谣言源。首先,采用随机游走策略来计算每个节点与观测节点之间的影响力向量。其次,设计了一个自编码器(AE)神经网络,将节点映射到潜在空间。然后,通过节点嵌入计算出节点是源节点的概率并定位谣言源。在6个网络上的实验结果表明,本文的DL-SIA方法可以更有效地定位谣言源。
在社交网络中,个体之间的关系和边上的传播概率可能经常变化。许多社交网络由在线和离线用户、关注和不关注的用户组成,这影响了社交网络的拓扑结构,造成了传播过程中的巨大变化。因此,谣言源定位策略应作出相应改进。目前,很多研究人员都在关注动态社交网络中的影响力分析,如链接预测、影响力传播最大化等。然而,动态网络中的不稳定因素和高计算复杂性使得动态网络中的谣言源定位问题更具挑战性。未来的研究将利用深度学习方法设计更有效的方法来定位这种动态网络中的多谣言源。
