改进麻雀搜索算法的飞行器航迹规划
2024-03-19李云舒张宏强赖灿辉
雷 刚, 李云舒, 张宏强, 罗 炜, 赖灿辉
(1.火箭军工程大学,西安 710000; 2.火箭军装备部某军代室,武汉 430000)
0 引言
飞行器航迹规划是考虑飞行器状态约束和环境约束条件下,为完成飞行任务而设计的飞行轨迹。从20世纪70~80年代开始,许多学者对航迹规划问题进行了探索,根据规划层次不同,可分为离线航迹规划和在线航迹规划。在离线航迹规划中,环境约束是已知或者部分已知,需要对飞行环境中固定的障碍物、禁飞区等进行规避。为了使飞行器与规划系统实现精确的交互,往往通过规划航迹节点[1]来实现。而一个航迹节点通常包括当前的位置坐标、俯仰角、滚动角以及偏航角[2],可将航迹规划问题转化成一个多目标节点优化选择问题。当不考虑其他条件约束或者飞行环境已知时,初始点到目标点的航迹优化似乎并不复杂,但是在实际的航迹规划过程中,往往需要考虑当前环境下的很多不确定性因素,比如移动雷达车的监测、强对流天气的影响等。这时往往不能按照之前的航迹点进行飞行,需要优先保证飞行器的安全性,在安全的条件下完成剩余的航程。
当前对于航迹规划的研究过程中,常用的有两类规划算法,一类是传统航迹规划算法[3],另一类是群智能优化算法[4]。在传统航迹规划算法中,王殿君等利用Dijkstra算法[5]和A*[6]算法基于多叉树理论,以起点作为根节点,采用节点回溯的方式,向目标点探寻最优路径,但是由于搜索算法会随着搜索维度的升高而出现组合爆炸的问题,在三维的航迹规划问题中计算速度较慢;文献[7-8]基于A*算法,采取稀疏搜索空间的方式,结合D*算法进行逆向搜索,在飞行过程中环境发生变化时,算法能根据新的环境信息删除原来的航迹节点,重新进行航迹规划,具有较好的实时性;人工势场法[9]的算法模型相对简单,路径规划过程中只需要通过传感器获取局部环境信息,在引力场和斥力场的共同作用下向目标点移动,但是在航迹中出现多个连续禁飞区时,会导致计算的路径收敛效果不稳定,出现局部震荡,在实际飞行中存在一定难度。群智能优化算法由于其具有内在的并行性和随机性,在多目标约束问题中展现出了优良的寻优能力。文献[10]融合快速搜索随机树(RRT)算法和人工势场法的优点,将目标点与禁飞区的合力方向作为过程树的搜索方向,利用改进的RRT算法生成航迹点作为初始种群,利用遗传算法对飞行器航迹进行了快速规划;汤安迪等[11]针对无人机航迹求解中计算复杂、收敛性差的问题,在二维任务空间模型与航迹代价模型的基础上,将立方映射混沌算子引入麻雀搜索算法(SSA),提高了初始种群的均匀性及多样性,同时采用高斯游走策略算法可以有效保证算法能跳出局部最优。
1 航迹规划环境模型建立
1.1 问题描述
飞行器在执行飞行任务时,需要考虑环境中的地形障碍、火力范围和雷达等干扰,因此在对任务环境的建模中,需要建立各类威胁区[12]。本文建立的三维地形描述如下
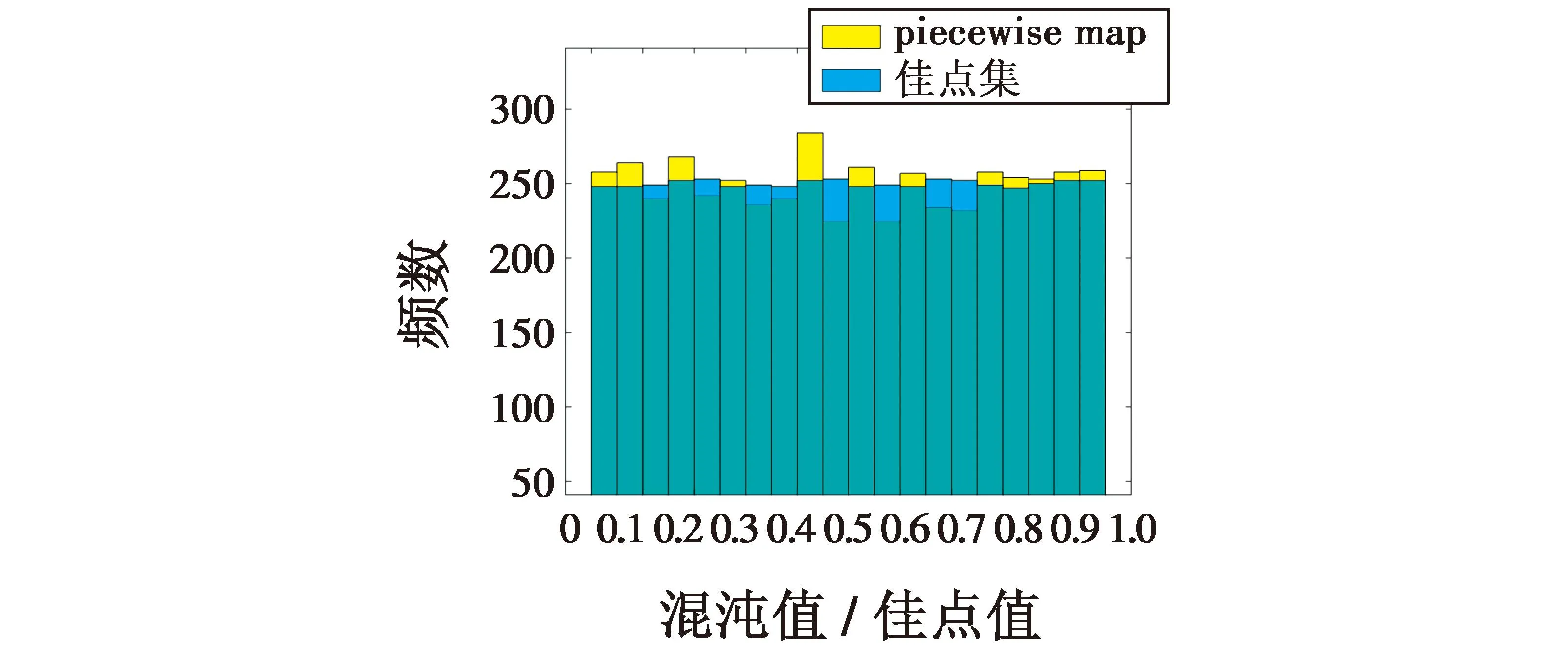
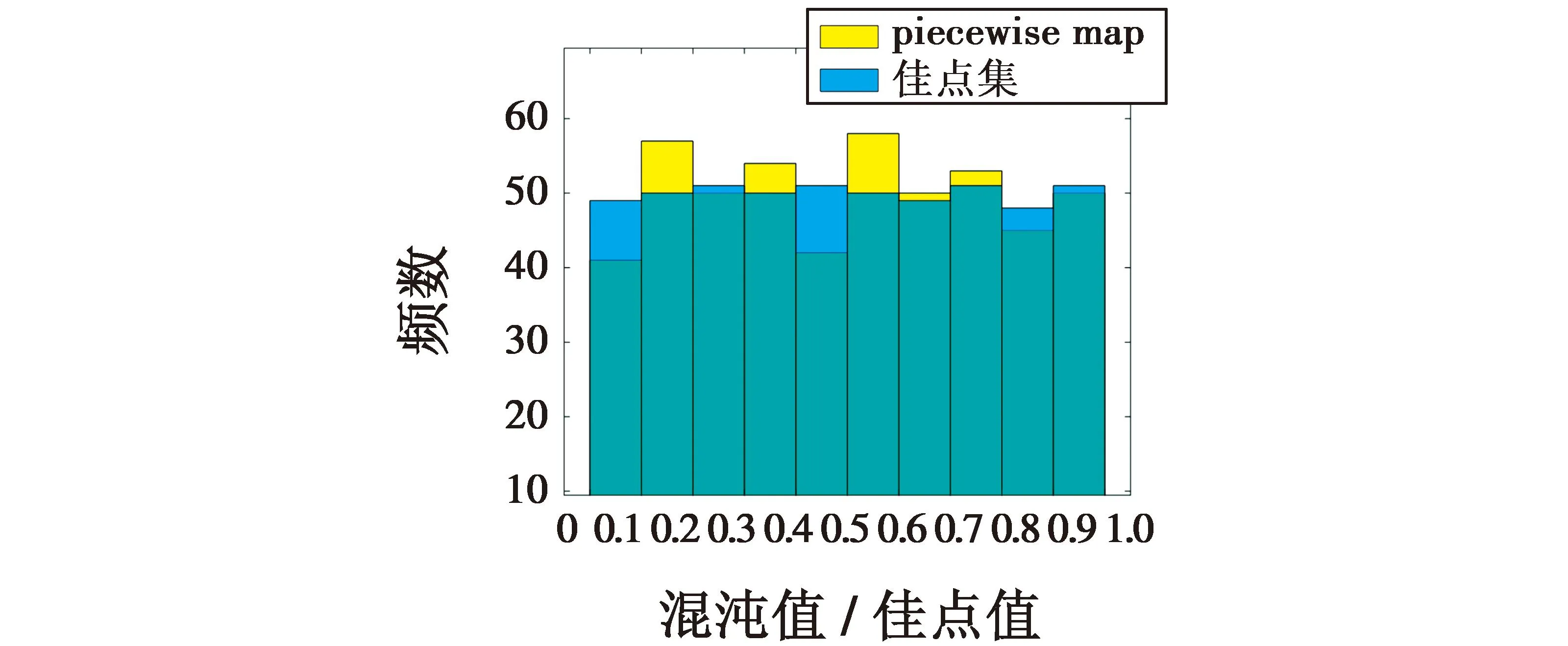
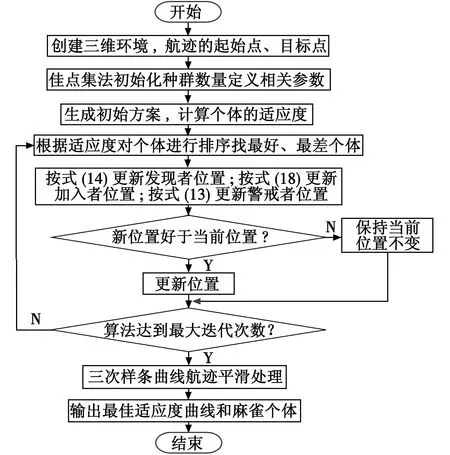
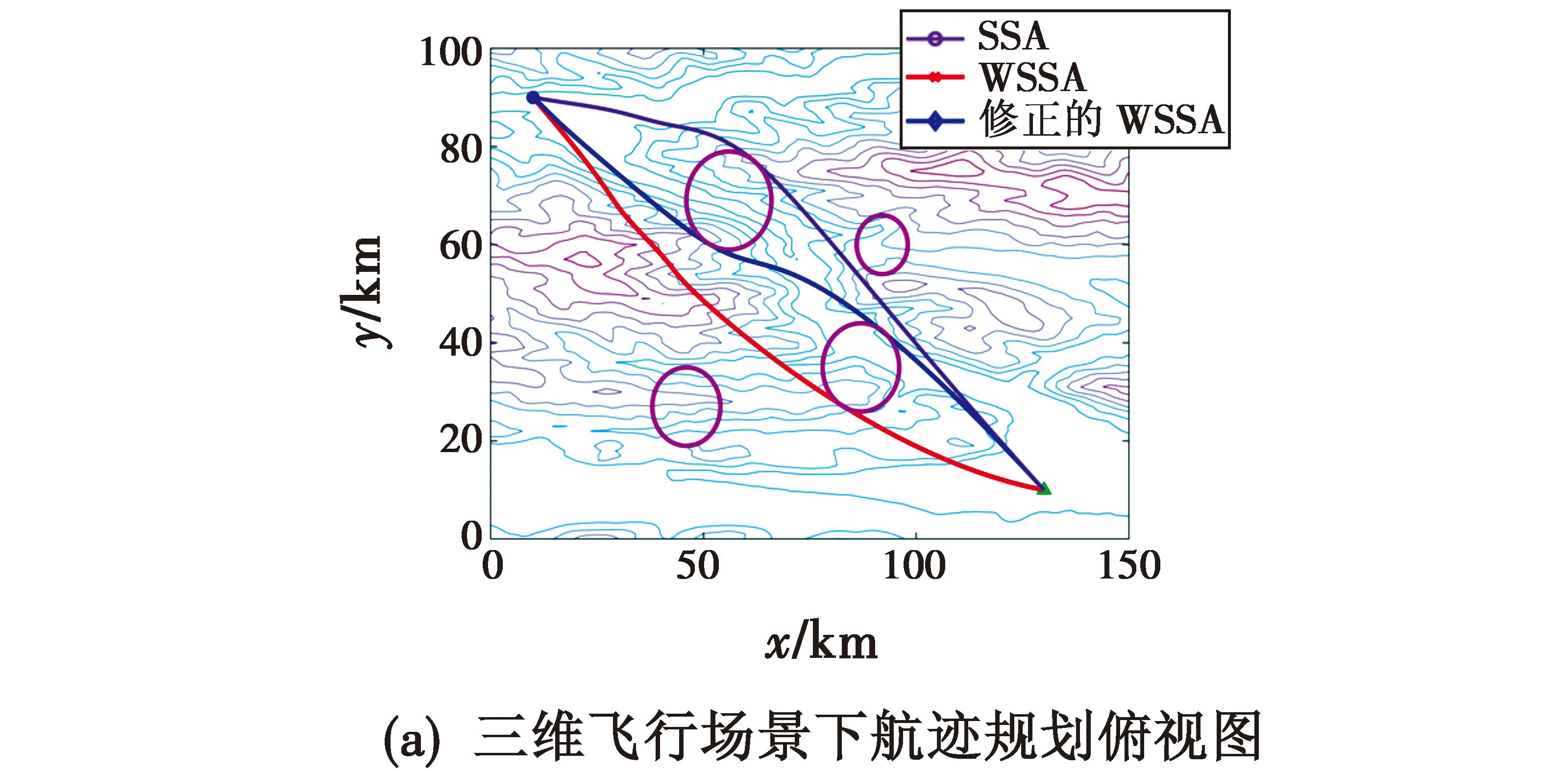
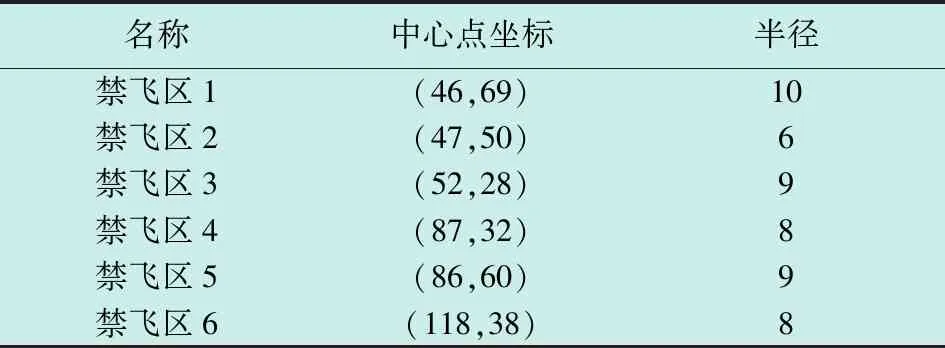
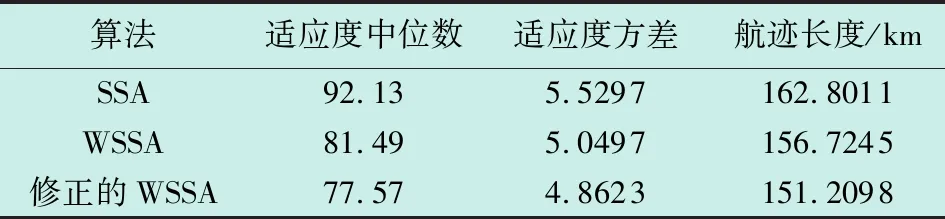
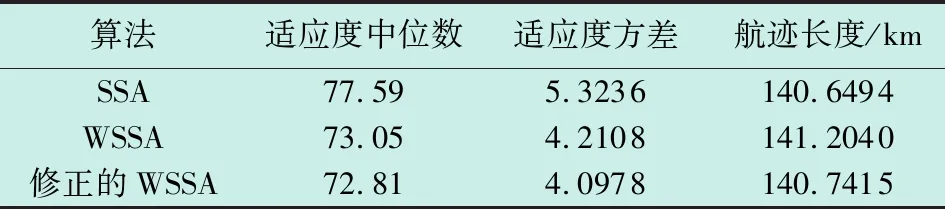
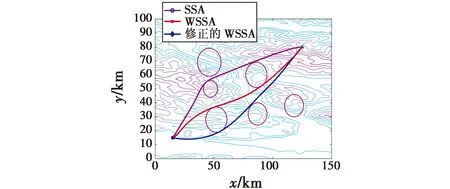
Φ={Xmin (1) 式中,*min,*max分别是*的下界和上界。在飞行器的避障过程中为了保证飞行器的稳定性以及隐蔽性,往往通过低空转弯进行障碍规避,本文主要考虑飞行器的离线静态规划。 飞行器在飞行过程中,受自身性能参数和气动特征的限制,需要考虑油耗、机动性、最小飞行高度等因素的约束,保证飞行器进行基本的飞行任务。航迹规划的准确性主要受飞行器自身的性能影响,主要考虑以下约束。 1.2.1 最大航程 飞行器通常携带的燃料一定,所以航迹的长短一定意义上决定了能否完成任务,记飞行器的任务航程为L,则L应该满足 (2) 1.2.2 最大转弯角度约束 角度约束包括了飞行器的偏航角约束和俯仰角约束两个参数,飞行器在转弯的过程中受到自身气动外形和惯性特征的限制,所以在转弯过程中,两个连续航点的转弯角不能超过最大转弯角,记最大转弯角为αmax,则αmax应满足 (3) 1.2.3 飞行高度约束 最小飞行高度是飞行器与当前地面的最小相对高度,较低飞行时,受益于地形提供的掩护,以及其他杂波会对雷达的探测产生一定干扰,所以为了提高飞行器的生存性,飞行高度应尽可能的低。设定一个最小高度ΔHmin和最大高度ΔHmax,飞行高度h应满足 ΔHmin (4) 1.2.4 最大爬升角约束 爬升角是速度方向与当前航迹点水平面的夹角,需要考虑最大爬升角约束来确定合适的起飞速度和起飞重量等参数,以确保飞机可以顺利地起飞并达到安全高度。设置最大爬升角为γmax,规划过程中的爬升角应满足-γmax≤γ≤γmax,且有 (5) 评价航迹算法优劣性的前提是建立良好的航迹评价指标,其中主要包括飞行器自身的性能约束、算法的优劣性以及航迹代价,在综合考虑飞行器的全程航迹规划下,建立如下航迹评价函数 minJcost=ω1·J1+ω2·J2+ω3·J3 (6) 式中:Jcost表示总的航迹目标;J1,J2,J3分别表示油耗代价、威胁代价、高度代价。 1.3.1 油耗代价 由于飞行器自身携带的燃料有限,相应任务的时间配比有限,假设飞行器在航迹规划的过程中保持匀速运动,油耗代价函数J1可以表示为 (7) 式中,c为油耗系数。 1.3.2 威胁代价 规避威胁区域实现安全突防是航迹规划的主要任务,威胁区主要分为地形、雷达探测、气象等。本文中将威胁区域简化为圆柱体区域,规定飞行器不能通过该区域。威胁代价函数表示为 (8) 式中:N-1表示式(3)中Ai的路径段数目;Ti为第i个威胁区域对航迹的威胁代价。 1.3.3 高度代价 当飞行器的飞行高度低于规划区域或者高于规划区域时,不利于任务规划过程,高度代价函数简化为 (9) 式中,p1、p2均为比例系数。 麻雀搜索算法(SSA)是根据麻雀觅食并逃离捕食者的行为而提出的群智能优化算法,该算法的寻优过程属于发现者-跟随者模型[13],在该算法中,容易搜索到丰富食物的个体称为发现者,其他的个体则称为跟随者,种群中会有一定比例的个体进行预警,称之为警戒者。如果警戒者发现危险时,就会发出预警,发现者就会将其他个体带到安全区域,当个体中有新的加入者发现了更好的食物来源,那么就会成为新的发现者,而之前的发现者则变为跟随者,在此过程中种群发现者和跟随者所占种群数量的比例是不变的。 (10) SSA中发现者的位置迭代更新规则如下 (11) (12) (13) SSA航迹规划问题的寻优过程可以简单地解释为:每只麻雀个体代表一条可能航迹,麻雀的维度代表这条航迹上的航迹点个数,其个体的适应度代表了该航迹评价函数式(6)的适应度,发现者代表了当前航迹点处的较优个体,跟随者代表了当前航迹点处的次优个体,警戒者则代表了当前航迹点的约束,当约束超过临界值时放弃该航迹。按照SSA的更新迭代策略,不断更新t时刻下的较优位置,进行航迹点的优化选择。 经过多次验证,发现SSA和其他智能优化算法一样,受初始值的影响较大,而一组好的初始可行解往往可以加速种群收敛、提高解的精度,所以初始化种群的操作是非常有必要的。 2.3.1 佳点集优化初始种群 目前常用的种群初始化采用混沌映射、佳点集和反向学习等方法[14]。通过设置取值范围为[0,1],用piecewise map映射混沌算子和佳点集随机产生若干个点并进行统计,采用佳点集进行初始化种群处理,种群个数为5000和500的概率分布直方图分别如图1、图2所示。 图1 两种算法5000个点的分布图 图2 两种算法500个点的分布图 在迭代次数足够大的情况下,piecewise map映射处理和佳点集法处理的初始化种群均可以达到分散程度很高的水平。但是在小样本条件下,佳点集法处理的结果分布更加均匀,由于本文中采用的小样本,为了使分散更均匀,采用佳点集法进行种群初始化。 2.3.2 自适应权重的位置迭代更新 SSA的位置更新属于一种有导向性的搜索策略,全局搜索能力依赖于发现者的位置,对于发现者来说,原步长q服从正态分布,使算法整体的局部搜索能力变强,获得不错的适应度及精度,但是前期的全局探索过程中,较小的步长不利于全局搜索。在鲸鱼优化算法中,个体的位置更新迭代呈螺旋式上升,可以获取较好的全局搜索能力[15]。本文借鉴鲸鱼优化算法中迭代寻优的螺旋式上升搜索方式,引入自适应权重因子ζ,使得SSA中发现者在位置更新,探索下一次区域时前期以较大步长搜索,后期进行小步长收敛探索,改善后发现者的位置迭代式如下 (14) (15) 2.3.3 柯西-高斯变异 枪声定位系统中,节点检测的枪声信息中主要包括枪声到达声传感器阵列的时间,准确的时间信息能够优化系统的测试结果。在(DMTS)算法[12]的基础上,通过两次广播簇头的时钟信息来估算簇头和节点之间的相对频率偏差,并修正接收节点的本地时钟,时间同步算法流程如图6所示。 SSA在迭代后期,种群会逐渐地向着最好的个体靠拢,减弱了种群的多样性,方差可以很好地表示种群整体的波动情况,较大方差的变异因子可以让算法具备更好的突变能力,能更好地跳出局部特性,同时带来的弊端是会影响局部寻优的精度和速度。而局部寻优过程中方差较小的变异因子能更快速地收敛函数,使其达到极值,缺点是容易使算法陷入早熟。 本文模拟生物交叉、变异的特性,在算法中加入变异因子的种群进化机制[16]。高斯分布又名正态分布,表达式为 (16) 柯西分布与高斯分布类似,表达式为 (17) 两种分布如图3所示。 图3 高斯分布和柯西概率密度函数 由图3可知,柯西分布比高斯分布的分布范围广,容易产生距原点更远的随机数,有更大的概率跳出局部最优,但是柯西分布的期望和方差不存在,本文结合高斯分布和柯西分布的优点,考虑不同搜索阶段的变异需求,设计柯西-高斯变异机制,方便保留较好适应度位置的麻雀个体,进入下一次迭代,即 (18) 将本文改善后的算法用于飞行器的航迹规划问题,算法流程如图4所示。 图4 修正的WSSA流程图 表1 禁飞区位置分布 z轴坐标数据由Global Mapper 20软件处理的高程数据用仿真软件插值产生,加入禁飞区约束后的三维模型环境如图5所示。 图5 加入禁飞区约束后的三维模型环境 3.2.1 算法适应度 根据上述条件,使用SSA、WSSA以及加入柯西-高斯算子修正的3种算法分别在此三维模型环境进行离线航迹规划,设置仿真次数为100,在每次实验过后记录3种算法的计算用时、适应度等。3种算法的适应度寻优过程如图6(a)~6(c)所示,适应度的平均值对比如图6(d)所示。 图6 3种算法适应度寻优过程与平均适应度曲线 3.2.2 结果分析 如图6(c)、6(d)所示修正的WSSA由于加入了柯西-高斯变异因子,导致算法前期适应度曲线的颠簸程度较大,但是搜索中后期能够快速集中收敛。这也从侧面验证了算法前期和后期都具有良好的全局搜索能力,优化结果如表2、图7所示。 表2 航迹规划结果比较 图7 3种算法的收敛箱式图 WSSA在平均适应度值、最差值、最优值等方面都是较优于原SSA的,而修正的WSSA则适应度最优最劣值的范围波动较小,更有利于快速收敛到较优的可行解。航迹规划结果如图8所示。 图8 航迹规划结果 为探寻算法在其他环境条件下是否依旧具有优势,本文基于同地图不同禁飞区约束下和不同地理环境进行了测试。 3.3.1 不同禁飞区位置测试 保持地理三维模型不变,更新禁飞区的位置和数量,更新后的禁飞区位置如表3所示。 表3 新的禁飞区位置分布 设置仿真次数为100,依次用3种算法进行路径寻优,优化结果如图9和表4所示。 表4 多禁飞区下航迹规划结果比较 图9 多禁飞区下的俯视图 如表4所示,受到多个禁飞区的影响,适应度值随着仿真次数的增加而出现波动较大,总体的适应度方差大的情况,但是修正后算法的方差波动相对较小,且航迹长度和适应度都相对更小。 3.3.2 不同起点、不同禁飞区位置测试 引用表4禁飞区位置的同时,改变起始点和目标点的位置。设置任务起点(15 km,15 km),目标点(125 km,80 km),仿真次数为100,依次用3种算法进行路径寻优,优化结果如图10和表5所示。 表5 多禁飞区下航迹规划结果比较(起始点不同) 图10 多禁飞区下的俯视图(起始点不同) 受到多个禁飞区的影响,适应度值随着仿真次数的增加而出现波动较大,但是修正后算法的方差波动、航迹长度和适应度都相对更小。 综上所述,3种算法都可以对禁飞区以及地形进行有效规避,随着地形复杂程度变高、禁飞区的数量变多,修正的WSSA依然在计算时间、适应度值以及航迹的平滑程度具有优势。 本文基于禁飞区的规避问题,建立了三维环境模型以及航迹评价指标。采用智能优化算法探寻其最优航迹。为避免不好的初始解会影响算法的寻优效率和种群多样性,采用佳点集法进行了种群初始化处理;为提高算法搜索能力的同时保证算法的收敛性,借助鲸鱼算法中螺旋式搜索因子形成自适应权重迭代因子,有助于算法的过程寻优;为防止算法早熟,陷入局部最优解,在跟随者位置更新中加入柯西-高斯变异因子提高算法的全局寻优能力。实验表明,修正的WSSA在考虑禁飞区约束的航迹规划问题研究中展现出了较好的适用性和鲁棒性。1.2 性能约束
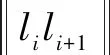

1.3 航迹评价指标
2 多策略改进麻雀算法的飞行器航迹规划
2.1 麻雀搜索算法
2.2 SSA流程
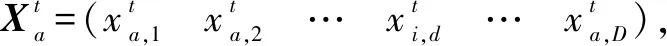
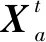
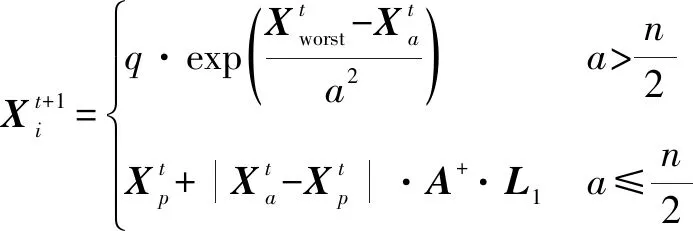
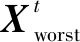
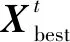
2.3 SSA的改进
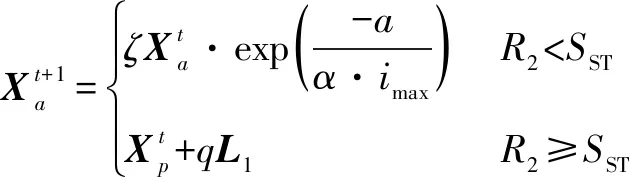
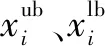

2.4 算法实现
3 仿真实验与结果分析
3.1 仿真环境初始化


3.2 较少威胁区域的航迹规划仿真实验
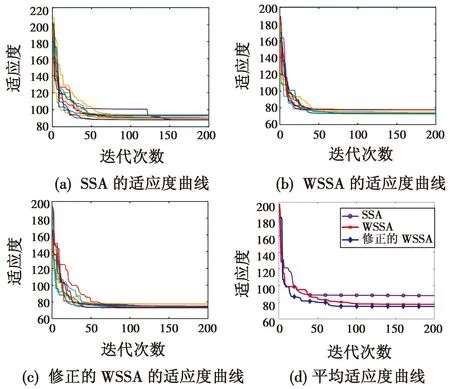
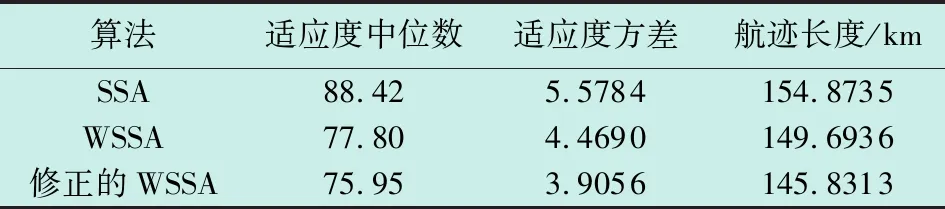
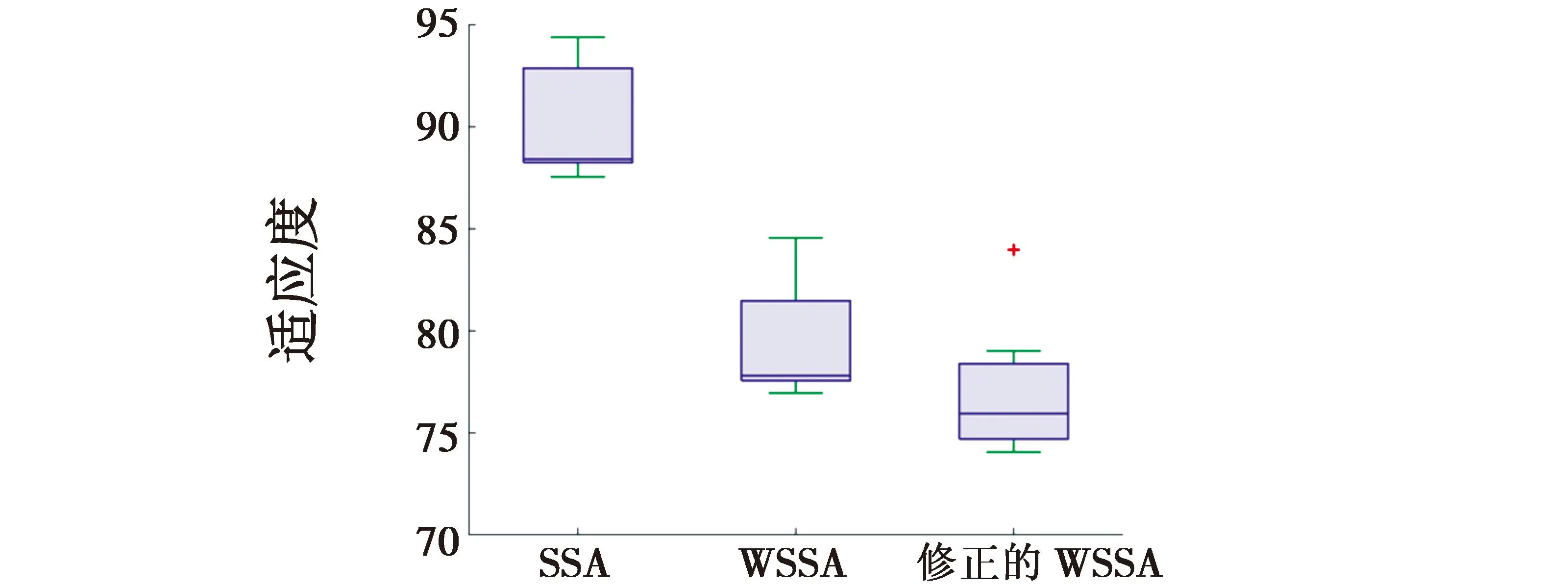
3.3 较多威胁区域的航迹规划仿真实验
4 总结
