基于Mindlin解的自锚试桩Q-s曲线研究

2024-03-19张钢泉马海龙

水利规划与设计 2024年3期

张钢泉，马海龙

(浙江理工大学，浙江杭州 310018)

0 引言

自锚试桩法分上、下两段桩，上段桩为抗拔桩、下段桩为抗压桩，通过千斤顶对上、下段桩施加大小相等方向相反的荷载，通过自锚试桩试验可同时获得上、下段桩的Q-s曲线，现有文献对计算获得自锚试桩Q-s曲线的研究较少。朱琳[1]利用三折线传递函数模型推导了自锚试桩上、下段桩的Q-s曲线解析公式。Chen chi等[2]基于自锚试桩室内试验、原位试验结果，提出以双曲线函数模型模拟自锚试桩的荷载传递关系。

自锚试桩上段桩为抗拔桩，对于抗拔桩的变形计算，黄峰等[3]考虑桩的伸长变形、桩周土体不均匀性、应力路径等影响因素，结合剪切位移法，推导了砂土中抗拔桩荷载-位移关系的理论解。黎玉琪[4]将抗拔桩的位移分为桩土界面内、界面外位移，通过3种不同桩土界面模型对抗拔桩的位移进行计算分析。Faizi等[5]通过室内试验与有限元软件分析，认为抗拔桩的长细比对桩体抗拔承载力影响较大。孙晓立等[6-7]给出了确定抗拔桩变形研究中土体力学参数的计算方法，提出了预测抗拔桩变形的弹塑性解析方法和修正变形协调法。何慧斌等[8]基于荷载传递理论，提出以迭代算法计算抗拔桩位移。

自锚试桩下段桩为抗压桩，对于抗压桩的沉降计算，王金淑等[9]基于Mindlin位移解，引入地基沉降修正系数，建立了基底沉降计算的双曲线切线模量法。Ma hai long等[10]通过对抗拔桩和抗压桩的室内试验，发现抗拔桩和抗压桩分别对桩侧土产生卸载、加载效应。陈贤可等[11]通过桩网复合地基的室内模型试验研究发现桩侧总摩阻力会随循环荷载次数增加而减小。张芳芳等[12]通过对刚-柔性长短桩复合地基的承载力与沉降变形研究，发现刚性长桩可控制沉降变形。费勤发[13]将分层总和法应用于单桩分析中，并提出消除地面负沉降影响的公式。何思明[14]在分层总和法基础上，考虑土体的三向应力，引入土体弹塑性本构关系分析土体的变形。李仁平[15]考虑基础埋深、土体非线性等影响因素，引入附加应力修正系数，利用双曲线切线模量方程和附加应力弹性解计算地基沉降。Sharo Abdulla等[16]基于荷载传递法，采用三线性软化模型、双曲线模型分别模拟桩周土位移、桩端位移与摩阻力的关系。Ma Danan等[17]研究了粉土中钻孔桩的沉降机理，分析了桩周土的密度、比重、天然含水率等因素对沉降的影响。王涛等[18]将桩基侧阻分布概化为4种形式，提出Mindlin解均化应力分层总和法计算群桩基础沉降。陈明中等[19]考虑了桩土间的滑移、土体强度变化等因素，推导了计算单桩沉降的解析表达式。

综上，对于抗拔桩和抗压桩的变形计算，国内外学者一般采用弹性理论法、荷载传递法、剪切位移法、分层总和法等。本文根据自锚试桩室内试验结果，基于Mindlin应力解，利用双曲线切线模量修正地基变形模量，以考虑不同深度处地基的非线性变形，避免Mindlin解无法考虑土体非线性变形的情况，并将其应用于分层总和法中，推导了计算自锚试桩上、下段桩变形的公式，为研究自锚试桩的变形计算及向传统试桩的Q-s曲线转换提供参考。

1 变形公式推导

分层总和法是一种简化的计算方法，在沉降计算中通常只考虑桩端平面以下的土层压缩，而忽略了桩侧土的压缩量，实际桩沉降量为桩侧土压缩与桩端土压缩之和。将自锚试桩的上段桩及桩侧土层按土层分布均匀划分为n个单元；将自锚试桩下段桩桩顶至压缩层计算深度处的土层按其土层分布均匀划分为k-n个单元。将自锚试桩的下段桩按土层分布均匀划分为m个单元，并考虑下段桩桩端平面为1个单元，下段桩共计m+1个单元。以字母i代表桩单元，i的取值范围i=1～(n+m+1)，字母j代表土层单元，j的取值范围为j=1～k。

土层的压缩层计算深度可按下式确定：

σ0=0.2σZ

(1)

软土地区压缩层计算深度可按下式确定：

σ0=0.1σZ

(2)

式中，σ0—计算深度处的附加应力，Pa；σz—计算深度处土的自重应力，Pa。

1.1 下段桩沉降公式

自锚试桩下段桩为抗压桩，上段桩为抗拔桩。根据文献[20]可知，自锚试桩加载过程中，上、下段桩相互作用较小，故对下段桩沉降计算时不考虑上段桩加载对下段桩沉降的影响，认为下段桩的沉降只与下段桩自身的桩侧摩阻力和桩端阻力有关。

1.1.1桩侧摩阻力产生的沉降

如图1所示，将自锚试桩第i单元桩侧微面积上的摩阻力作为集中力qirdθdc，将其代入Mindlin应力解，则桩第i单元上的集中力对土层第j单元产生的附加应力σj，i可表示为：

(3)

图1 单元划分

附加应力σj，i对土层第j单元产生的微量竖向压缩变形可表示为：

(4)

式中，Ej—土层第j单元的地基变形模量，Pa。

附加应力σj，i对土层第j单元产生的全部竖向压缩变形sj，i可用下式计算：

(5)

式中，zj-1—土层第j单元上表面的埋深，m；zj—土层第j单元下表面的埋深，m。

将式(5)解积分得：

+2π(C1-C2)

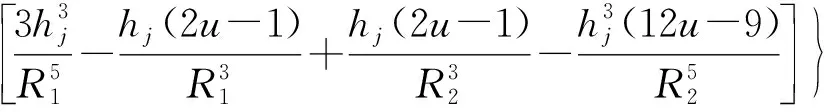
(6)

则土层第j单元受桩侧摩阻力作用产生的总竖向压缩变形可由下式计算：

(7)

将sj，i作简单拆分，令sj，i=qiIj，i。Ij，i—桩第i单元对土层第j单元的沉降系数；qi—第i单元上的平均侧摩阻力，Pa。

则各级荷载作用下，每一土层单元的竖向压缩变形可由下式计算：

(8)

将下段桩桩顶至压缩层计算深度范围内各土层的竖向压缩变形累加，即为下段桩桩侧摩阻力所产生的沉降量：

(9)

1.1.2桩端阻力产生的沉降

将下段桩桩端单元微面积上的桩端阻力以Pb表示，并将其代入Mindlin应力解，则桩端单元上的集中力对土层第j单元产生的附加应力σj，Pb可表示为：

(10)

附加应力σj，Pb对土层第j单元产生的微量竖向压缩变形可表示为：

(11)

则附加应力σj，Pb对土层第j单元产生的总竖向压缩变形为：

(12)

将式(12)解积分得：

(13)

将下段桩桩顶至压缩层计算深度范围内各土层单元的竖向压缩变形累加，即为下段桩桩端阻力产生的沉降量：

(14)

将下段桩桩端阻力、桩侧摩阻力产生的沉降量相加即为下段桩的沉降量：

s下=s端+s摩

(15)

2 上段桩变形公式

自锚试桩上段桩为抗拔桩，因自锚试桩上、下段桩相互作用较小[20]，故对上段桩的变形计算时不考虑下段桩加载的影响，认为上段桩的变形只与上段桩的桩侧摩阻力有关。

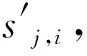
(16)

各土层单元的竖向压缩变形可由下式计算：

(17)

将上段桩桩周土层单元的竖向变形累加，即为上段桩的变形量：

(18)

3 变形模量E的修正

Mindlin解可用来求解各向同性弹性半空间体内集中荷载作用下的土体变形，但其存在一定局限。Mindlin解在计算过程中假设桩土界面为完全弹性接触，利用Mindlin解对土层进行变形计算时采用单一的变形模量参数，其计算结果仅能表达桩周土体在弹性阶段的荷载-位移关系，不能真实反映桩周土体内部复杂的塑性影响和非线性变形特征。由于对桩周土体处于塑性破坏阶段的非线性变形无法体现，计算与实际情况存在较大误差。

基于此，本文参考文献[15]中的修正方法，考虑地基土层埋深、地基非均质非线性等因素的影响，利用下式对土层的变形模量进行修正，以计算桩的非线性变形。

Et=E0(1-0.8βpzi/pui)2/β

(19)

式中，Et—修正变形模量，Pa；pzi—土层第i单元处的总附加应力值，Pa；pui—土层第i单元处的附加极限应力，Pa；β—附加应力修正系数，一般取0.9，E0—地基变形模量，Pa。

pu可按下式计算：

pu=cNc+γD(Nq-1)

(20)

式中，Nc，Nq—抗剪强度指标有关的承载力系数；c—土体粘聚力，Pa；γ—基底以上土的加权重度，kN/m3；D—基底埋深，m。

Nc，Nq可按下式计算：

(21)

Nc=(Nq-1)·cotφ

(22)

式中，φ—土体内摩擦角，(°)。

地基变形模量E0按下式计算：

(23)

式中，ES—地基压缩模量，Pa；u—土体的泊松比。

4 计算Q-s曲线验证

本文理论分析所采用的计算参数取自文献[1]，土体主要物理力学参数见表1。将表中数据代入公式(20)—(22)可分别计算得Nq、Nc为11.85、22.25，地基附加极限应力pu为132.21kPa，再根据公式(19)、(23)，计算得各土层单元的修正地基变形模量Et以及地基变形模量E0。

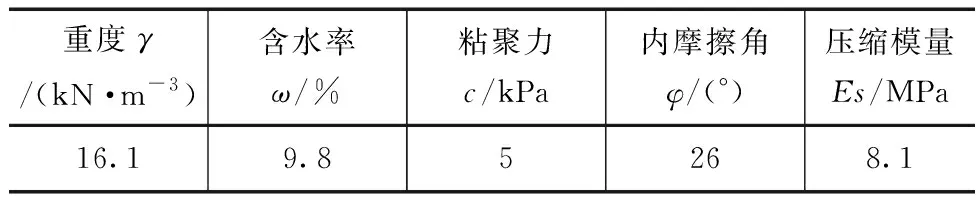
表1 土体物理力学参数

本次试验用土为单一土层，故单元划分无需考虑土层分布的影响。上段桩桩长为1.1m，将上段桩均匀划分为11个单元，每个单元长0.1m；下段桩长0.1m，将其划分为1个单元，再令桩端平面为1个单元，下段桩共2个单元。将上段桩桩侧土均匀划分为11个单元；根据式(1)可计算得下段桩压缩层厚度为0.3m，故将下段桩桩顶(1.1m)至压缩层计算深度(1.5m)范围内土体均匀划分为4个单元。

将前文推导的公式编写入matlab数值分析软件，再将室内模型试验中实测得到的各工况下桩侧摩阻力、桩端阻力代入公式(15)、(18)中，可分别得到自锚试桩上段桩和下段桩的Q-s曲线。

4.1 下段桩Q-s曲线对比

4.1.1下段桩Q-s曲线

如图2所示为采用修正变形模量、未修正变形模量的计算Q-s曲线与实测Q-s曲线对比。

图2 下段桩Q-s曲线

从图2中可以看出，采用未修正变形模量计算得到的自锚试桩下段桩Q-s曲线近似呈线性分布。在200N至600N荷载作用下，其沉降量计算值与实测值接近，可较好地反映试桩承受荷载低于650N(单桩竖向承载力特征值)的Q-s曲线变化规律，但在700～1300N荷载范围内，随着荷载增加，计算值与实测值的误差逐渐增大，在1300N极限荷载作用下计算所得的沉降量为0.69mm，而实测沉降量为2.42mm，后者为前者的3倍多。究其原因：采用单一的变形模量进行计算，假定土体始终处于弹性阶段，无法考虑到随着荷载增加桩周土内部产生的复杂塑性变化和非线性变形，导致塑性变化阶段的沉降量与实测值误差较大，且随着荷载增加，其误差会越来越大。而对于采用修正变形模量计算得的下段桩Q-s曲线，从图2中可见其变化规律与实测值一致，能较好反映自锚试桩下段桩的沉降随荷载的变化。

4.1.2桩侧、桩端阻力产生的沉降

下段桩桩端阻力、桩侧阻力都使下段桩产生沉降。如图3所示为下段桩在200～1300N荷载作用下，桩端阻力与桩侧阻力产生的Q-s曲线。

图3 桩端阻力、桩侧阻力沉降对比

由图3中可见，下段桩桩侧阻力所产生的沉降量随着荷载的增加变化较小，在200N荷载作用下为0.009mm，在1300N极限荷载作用下为0.011mm，相较加载初期仅增加了0.002mm。下段桩桩端阻力产生的沉降量随荷载的增加变化明显，加载初期200N荷载作用下为0.081mm，1300N极限荷载作用下为2.337mm。计算条件下的下段桩桩端阻力产生的沉降量远远大于其桩侧阻力产生的沉降量，其荷载主要由桩端阻力承担，桩侧阻力较小且在加载初期便很快完全发挥，因此下段桩的沉降主要由桩端阻力产生。

4.2 上段桩Q-s曲线对比

如图4所示为采用修正变形模量、未修正变形模量计算得到的上段桩Q-s曲线与实测Q-s曲线对比。从图4中可以看出，未修正变形模量的上段桩Q-s曲线呈线性分布，与实测值有较大误差。在200～600N荷载作用下，此时桩周土体处于弹性阶段，修正变形模量与未修正变形模量得到的Q-s曲线较为接近。

图4 上段桩Q-s曲线

而在600～1300N荷载作用下，随着荷载增加，桩周土体逐渐产生塑性变形，采用未修正变形模量得到的Q-s曲线与实测Q-s曲线产生较大误差，无法真实反映桩周土体内部的塑性变形。1300N极限荷载作用下，实测变形值为1.140mm，采用修正变形模量、未修正变形模量计算得到的变形量分别为0.982、0.689mm，故采用修正变形模量进行计算得到的Q-s曲线与实测值更为吻合，能较好反映自锚试桩上段桩的变形随荷载的变化情况。