自适应预测时域参数MPC车辆轨迹跟踪控制

2024-03-19吴长水高绍元

重庆理工大学学报(自然科学) 2024年2期

吴长水，高绍元

（上海工程技术大学机械与汽车工程学院，上海 201620）

0 引言

轨迹跟踪是无人车辆实现无人驾驶的重要环节之一，它是指通过根据某种控制理论，为车辆的控制系统设计一个控制输入作用，使得无人驾驶车辆能够以期望的速度跟踪目标轨迹［1］。经典的无人车辆轨迹跟踪控制算法主要有纯跟踪控制算法、滑模控制算法和PID算法等。这些算法在处理由车身、轮胎、悬架等组成的汽车非线性系统时存在不足，往往面临复杂、大量的调参工作［2］。对于多约束系统，MPC算法较其他控制算法具有先天性优势，能够很好地与路径规划、运动控制处理相结合，已成为无人车辆运动控制领域研究的热点。

MPC算法具有处理多个约束条件的能力：北京理工大学的孙银健等［3］为提高控制器的跟踪效果对侧偏角添加软约束处理。庞辉等［4］通过建立2自由度运动学模型，提出一种基于线性时变的MPC轨迹跟踪控制器，提升了自主车辆轨迹跟踪的精确性。近年来兴起的神经网络算法［5］也被广泛用于改善MPC算法的跟踪精度。上述研究多专注于通过简化车辆模型或优化约束条件来提高轨迹跟踪效果，所提出的方法对控制器仍存在较高的计算性能要求，出于成本的考虑，工业界常用的控制器算力是有限的，因此，为了降低算法的计算量，模型大多需要进行简化处理，如线性化、小角度假设等［6－7］。

预测模型是MPC算法用来描述整个系统动态行为的基础，MPC根据预测时域参数调整需要计算出系统状态量和控制量的次数。车辆的动力学响应是复杂多变的，参数自适应的MPC算法可以较好地适应这种特点：杜荣华等［8］提出了变预测时域MPC方法，通过模糊控制算法计算预测时域变化量实现预测时域的自适应调整；刘志强等［9］以最大横向偏差作为精度指标，通过综合评价法得到不同速度下预测时域和控制时域的最优取值。金辉等［10］通过改进粒子群算法优化权重参数和设计前馈神经网络的路面识别算法识别路面附着系数从而提升自适应权重控制器的跟踪效果。

基于上述研究，本文中提出一种自适应预测时域参数的MPC算法：以车辆在不同速度工况下轨迹跟踪过程中的最大横向偏差、最大横摆角偏差、仿真计算时间为评价项，通过灰色关联评价法确定预测时域参数与评价项的关联度。选定最优预测时域参数通过傅里叶逼近法进行拟合，最终得到可随车速变化的自适应调节预测时域参数的MPC控制器。通过仿真对比试验与实车测试，结果表明：所提出的自适应预测时域参数MPC轨迹跟踪控制器相较于传统固定预测时域MPC控制器能够有效减小轨迹跟踪控制超调量，在跟踪精度、求解速度和稳定性上都有明显提升。

1 车辆动力学模型

无人车辆的轨迹跟踪任务需要考虑车辆行驶过程的动力学特性，在保证跟踪精度的同时简化模型的复杂度可在一定程度上减小算法的计算量［11］。本文中所建立的车辆动力学模型如图1所示。其中：XOY为大地坐标系；xoy为车身坐标系；Fcf、Fcr表示前、后轮的侧向力；Flf、Flr分别为前、后轮纵向力；a、b分别为前、后轮到车辆质心的距离；δf为前轮转角；φ、˙φ分别为车辆横摆角、横摆角速度；αf、αr分别为前后轮侧偏角；β为质心侧偏角；Vf、Vr分别为车身坐标系前后轮的速度；V为车辆质心位置的速度。

图1 车辆动力学模型

根据牛顿第二定律和魔术轮胎公式，结合车身坐标转换公式，得到的车辆动力学模型为：

式中：m为整车质量；和分别为车辆在大地坐标系下纵、横向速度；Iz为车辆绕z轴的转动惯量；和分别为车辆在车身坐标系中的纵向和横向速度；Ccf和Ccr分别为前后轮的侧偏刚度；Clf和Clr分别为前后轮的纵向刚度；sf和sr分别为前后轮的纵向滑移率。选取系统的状态量为：ξ＝［，φ，，Y，X］T；控制量为u＝［δf］。

2 自适应预测时域参数MPC控制器设计

2.1 预测模型

根据式（1）的车辆动力学模型建立非线性动力学方程：

式中：f（ξ，u）＝［fy fx fφ f˙φ fY fX］T；Yc为控制输出量，Yc＝［Y φ］T；C为输出矩阵，C＝［0 0 1 0 0 0； 0 0 0 0 1］T令当前时刻系统的状态量和控制量分别为ξ0、u0，得到非线性模型：

式（3）中对任意点（ξ0，u0）进行泰勒展开并忽略高阶项，得到：

式（3）与式（4）作差，离散化处理后得到新的状态方程：

模型预测控制需要计算出预测时域内所有的状态量和控制量，通常采用增量作为实际控制量［12］，在此构建新的状态量如式（6）所示：

式中：η（k｜k）＝［ξ（k｜k）u（k－1｜k）］T，其中ξ（k｜k）为车辆在k时刻的状态量，u（k－1｜k）为车辆在k－1时刻的控制输入量，k时刻控制增量Δu（k｜k）＝u（k｜k）－u（k－1｜k）；Ck＝［C0］。

定义Np为预测时域参数，Nc为控制时域参数，在整个预测时域内对于预测模型的输出进行迭代计算，得到未来某时刻k的输出为：

2.2 目标函数及约束条件设计

在实际的控制对象中，系统的控制量偏差无法通过测试直接获得［13］。本文中轨迹跟踪控制器以控制车辆前轮转角为目标，这里将目标函数的控制量设置为转角增量，设计目标函数的目的是让车辆轨迹跟踪时能在拥有较高精度同时考虑车辆的行驶稳定性［14］，控制器跟踪的目标函数为：

为便于计算机求解，将式（8）转化为标准二次规划形式进行求解：

控制器是通过控制车辆前轮转角来执行轨迹跟踪任务，这里对每个计算周期内的转角范围和转角增量进行如下约束：

控制器在每个周期滚动优化求解，得到控制时域内一系列控制增量：

将式（11）中的第一项作为前轮转角的控制量输入给被控车辆，重复求解过程，实现轨迹跟踪的闭环控制。

2.3 自适应预测时域参数模型

2.3.1 控制器架构设计

在基于MPC的轨迹跟踪任务中，预测时域参数Np的选取对于跟踪的实时性和精度有较大影响。由于跟踪过程中车辆的实际行驶速度、道路曲率等复杂因素是时刻变化的，固定预测时域的MPC控制器处理这类变化的能力较弱［15］。如图2所示，自适应预测时域参数MPC控制器主要由3部分组成：MPC控制器、被控车辆模型、自适应预测时域参数模型。其中MPC控制器根据目标跟踪轨迹和目标函数求解出最优控制量作用于被控车辆，被控车辆将当前的车辆状态作为预测模型的输入，自适应预测时域参数模型根据目标车速求解出当前速度工况下的最优预测时域输入给MPC控制器，重复上述过程，最终实现变预测时域轨迹跟踪控制。

图2 自适应预测时域MPC控制器架构

2.3.2 预测时域与评价参数关联性分析

MPC预测时域参数往往依靠调试经验选取。当预测时域参数很大时，控制器可以预测较远的距离，同时也会造成车辆提前转向，降低轨迹跟踪精度；当预测时域参数较小时，在前轮的转向角度约束的影响下，车辆又会因无法及时转向而造成轨迹跟踪失败。为了探究预测时域参数与被控车辆状态响应的关系，采用灰色关联法［16］，选取预测时域参数Np项作为母序列，以最大横向偏差、最大横摆角偏差、仿真计算时间作为特征序列（评价项）来分析各评价项对母序列的关联程度。其中，最大横向偏差反映跟踪精度，最大横摆角偏差反映乘坐舒适性，仿真计算时间反映控制器求解速率。以10 km／h作为速度间隔，在10～120 km／h速度区间内设置不同的预测时域参数对控制器进行离线仿真实验，总实验组数为300组。同时，为了保证控制器时域参数的有效性，对预测时域参数进行以下筛选：1）选取的预测时域参数在跟踪试验中有较高的跟踪精度。2）选取的预测时域参数在跟踪试验中未发生超调现象。3）选取的预测时域参数在跟踪实验中未发生横摆角震荡现象。基于以上筛选条件，得到满足要求的试验138组。为方便指标数据进行量纲一体化，对值较小的评价项乘以10，分辨系数取0.5，得到的母序列预测时域参数Np与各子序列评价项的关联系数如图3所示。

图3 预测时域参数N p与评价项关联系数图

根据关联系数计算各评价项对Np的灰色关联度：

式中：rn评价项对预测时域的灰色关联度；ˉωi为第i个指标变量的权重，这里取等权重1／138；ζNp为预测时域关联系数。

根据式（12）得到的灰色关联度排名结果如表1所示。

表1 灰色关联度排名

结合图3和表1可以看出：针对3个评价项，最大横摆角偏差与预测时域Np关联度最高，且控制器求解时间很大程度上受预测时域参数的影响，其数据值的分布呈现一定的周期性。

以上文的时域灰色关联度结果为基础，在实验数据中以最大横摆角偏差的最小值为参考项选取出不同车速下的预测时域最优数据组。采用傅里叶逼近法［17］对预测时域参数和速度参数进行拟合，同时为防止过拟合，以仿真计算时间作为权重量，最终得到基于车速变化自适应预测时域参数模型如式（13）所示：

式中：a、b、ω为时域傅里叶拟合系数；x为车辆在大地坐标系下的纵向速度。

3 试验与分析

3.1 预测时域仿真对比试验分析

为了直观看出不同预测时域对轨迹跟踪控制过程的影响，搭建Matlab／Simulink与CarSim联合仿真平台进行仿真试验分析。在CarSim中选择轴距为3 050 mm的E级车作为被控车辆模型，车辆基本参数如表2所示，MPC控制器参数如表3所示。以50 km／h和100 km／h为代表车速，设计3组不同的Np值进行仿真测试试验，参考轨迹选择双移线避障轨迹，仿真试验结果如图4和图5所示。

表2 车辆基本参数

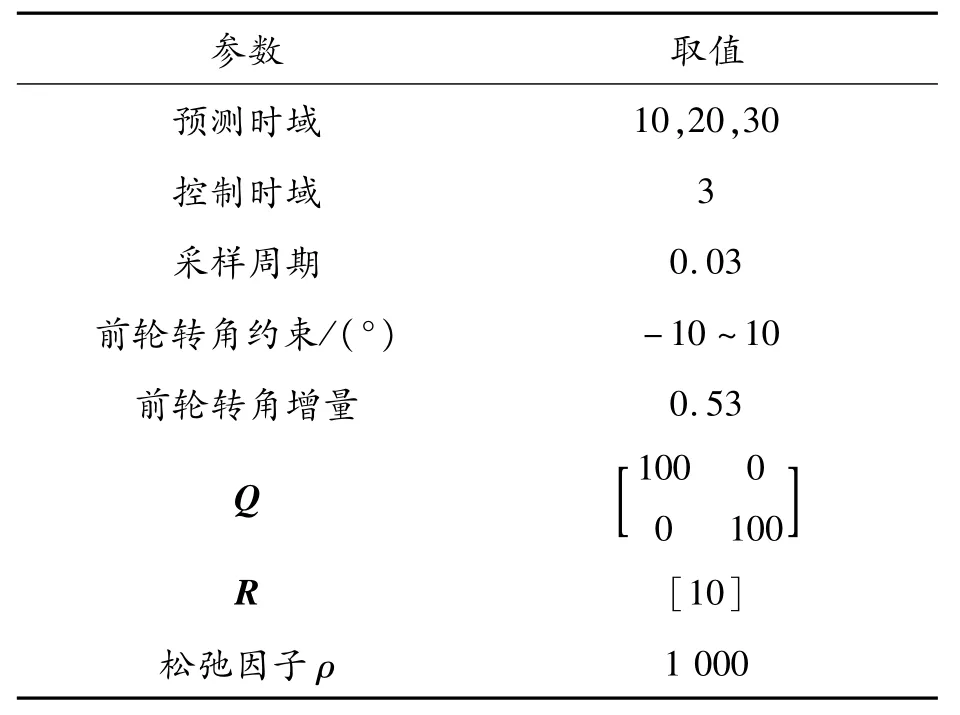
表3 控制器参数

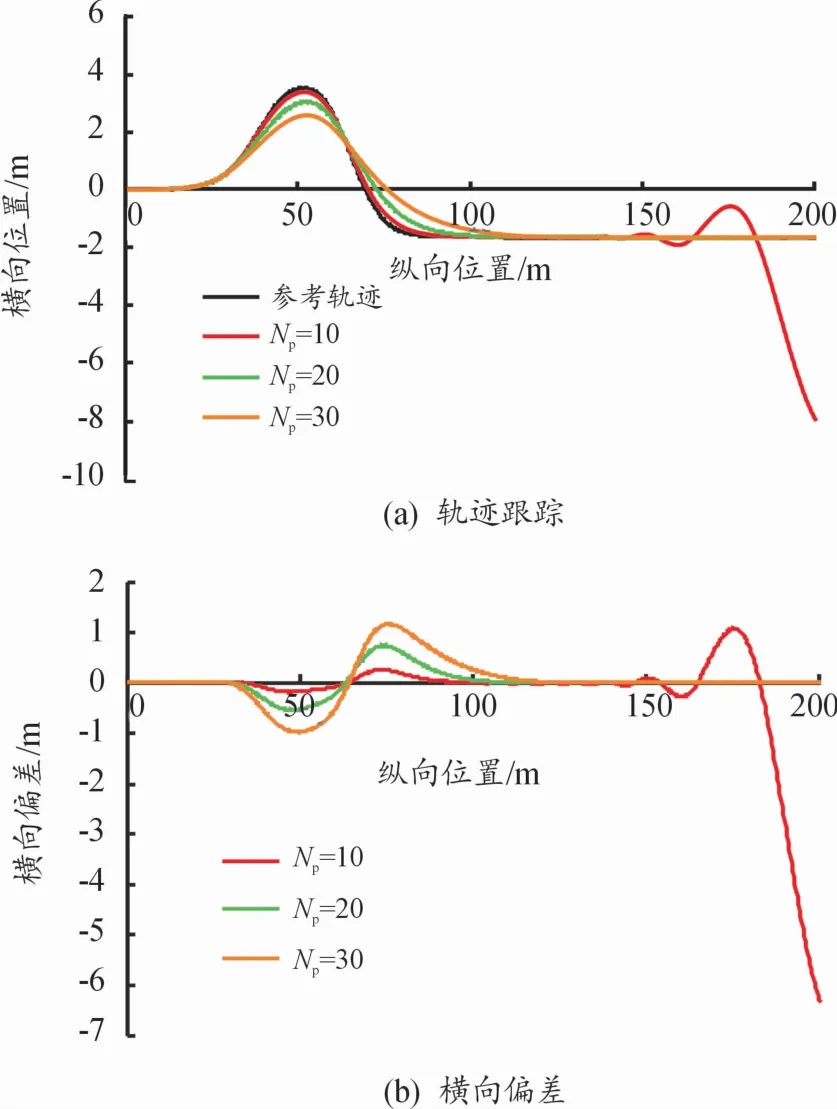
图4 50 km／h轨迹跟踪控制效果

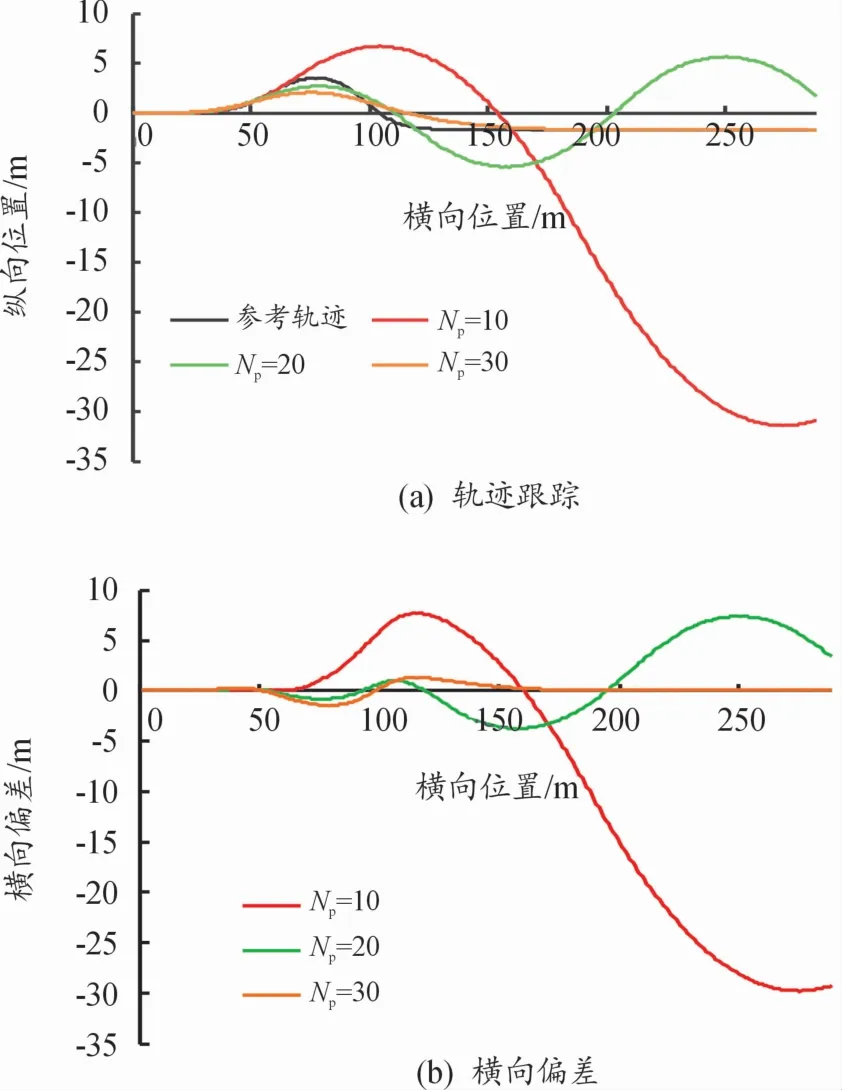
图5 100 km／h轨迹跟踪控制效果

由图4可知：不同的预测时域对控制器轨迹跟踪的效果有所差异。预测时域参数为10时，控制器跟踪双移线轨迹的横向偏差最小，但在跟踪直线轨迹时出现了严重的超调量，横向偏差逐渐增大为6.5 m，轨迹和航向已经完全脱离目标值。当预测时域参数为30时，控制器能够完成跟踪任务，但相比于预测时域参数为20时，其横向偏差较大，跟踪存在一定的滞后性。

结合图4和图5可以看出：随着目标跟踪车速的增加，当预测时域参数仍取10时，车辆在参考轨迹大曲率处出现了较大的偏移，这表明在不同速度工况下，固定预测时域参数MPC控制器对复杂路况的跟踪效果与车速变化具有较强的相关性。

3.2 自适应预测时域控制器仿真试验分析

式（13）的自适应预测时域参数模型的本质作用是在保证控制器跟踪精度和稳定性的基础上通过选取相对最优的预测时域参数来减小算法的计算量，降低控制器SOC的算力要求。本文中所设计加自适应预测时域参数控制器在双移线轨迹下的预测时域参数与目标车速、计算时间的变化规律如图6所示。

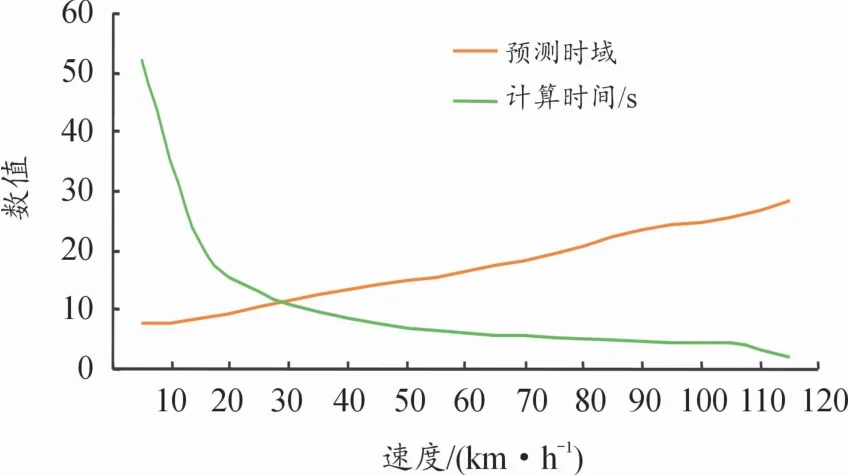
图6 预测时域参数变化规律

为了验证自适应预测时域参数MPC控制器的跟踪性能，在双移线避撞轨迹下与定时域MPC控制器仿真结果做对比，选取50、100 km／h为代表车速，经自适应预测时域模型计算出的预测时域参数取整后的值为：当车速为50 km／h时，Np＝14；当车速为100 km／h时，Np＝24；其他参数取值保持不变，仿真结果如图7和图8所示。

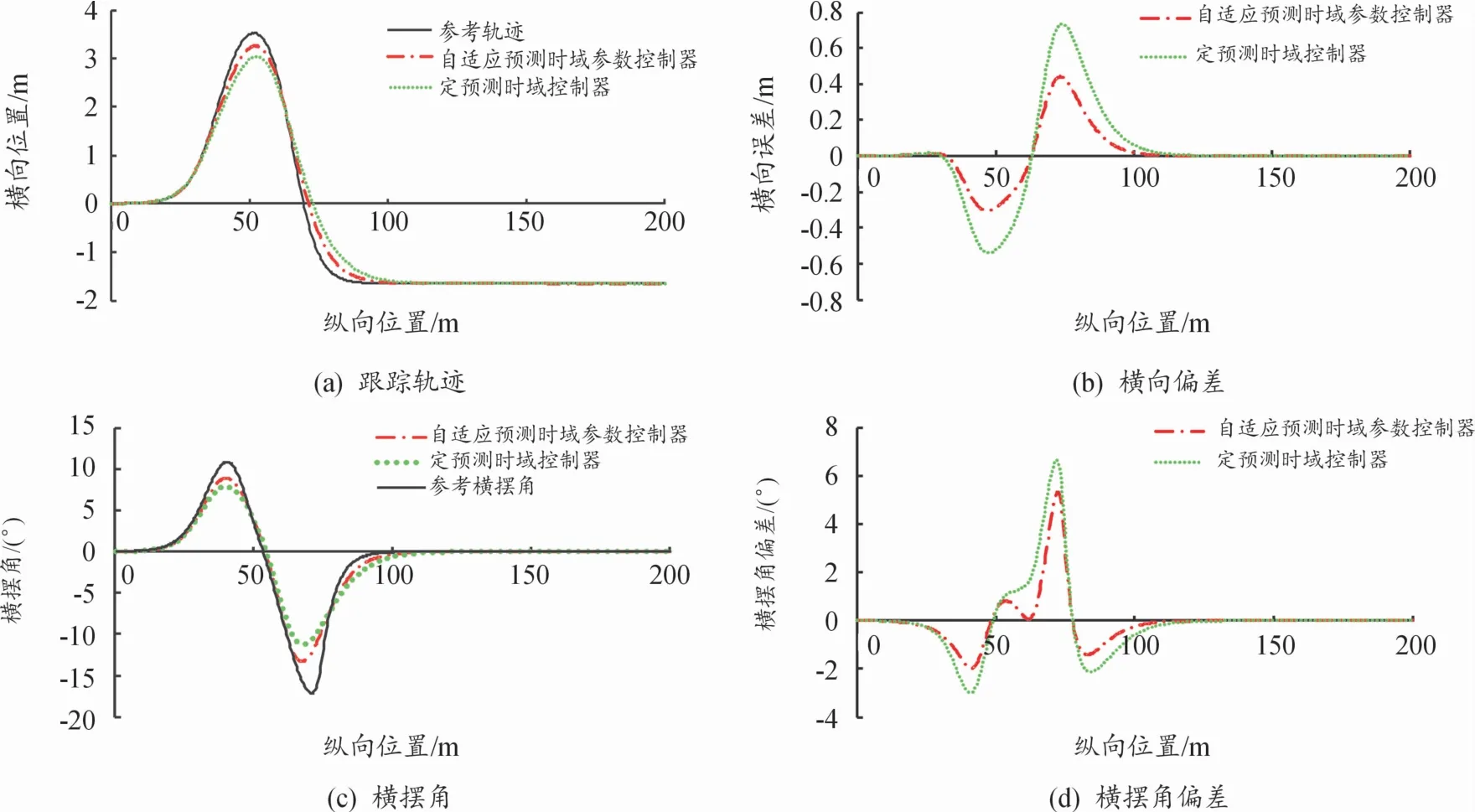
图7 50 km／h轨迹跟踪控制效果

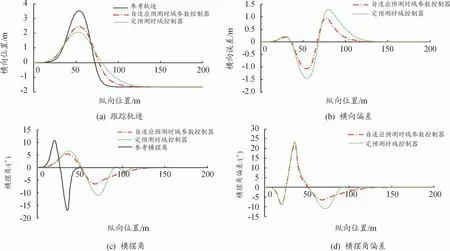
图8 100 km／h轨迹跟踪控制效果

从图7和图8易看出，不同速度工况下，自适应预测时域参数MPC控制器的轨迹跟踪效果要优于定预测时域控制器。在目标车速为50 km／h时，定预测时域参数控制器的最大横摆角偏差为6.66°，实测仿真计算时间为9.17 s，而自适应预测时域参数MPC控制器的最大横摆角偏差为5.33°，实测仿真计算时间为7.79 s，控制精度提高了19.9%，控制器求解速度提升了15%，自适应预测时域参数控制器的最大横向偏差、横摆角震荡幅度均小于定预测时域控制器。当速度达到100 km／h时，自适应预测时域参数控制器有效地减少了轨迹跟踪控制的超调量，其最大横摆角偏差和最大横向偏差较定时域控制器分别减小了0.5%、26.9%。说明在高速行驶工况下，自适应预测时域控制器的控制效果更好，车辆稳定性更高。

3.3 实车试验分析

3.3.1 试验方案

实车试验平台采用基于线控底盘车改装的无人驾驶车辆，如图9所示。该平台的车载感知层包括16线激光雷达、组合惯导、摄像头，执行器部分为线控底盘，控制器部分为基于Arm64架构的NVIDIA AGX orin域控制器和车载显示器组成。平台采用Ubuntu 20.04操作系统，通过Autoware.ai开源自动驾驶框架，可实现建图、定位、感知、规划和运动控制等一系列的自动驾驶关键功能。平台参数如表4所示。

表4 平台参数

3.3.2 试验结果

为验证所提出的自适应预测时域参数MPC控制器在真实道路环境下的轨迹跟踪效果，实车试验使用激光雷达采集道路环境的点云数据，通过NDT配准算法得到车辆在点云地图中的位姿信息，使用Autoware路径规划模块生成和保存车辆实际行驶的轨迹点［18］。试验车跟踪的轨迹如图10所示。

图10 试验车目标跟踪轨迹

由于中高速工况下的实车验证过于危险，实车测试试验设定的跟踪车速为5 km／h，每次试验从同一起点出发，测试结果如图11所示。

图11 实车测试验证结果

综合图11易看出：实车测试中，自适应预测时域参数控制器的轨迹跟踪效果要明显好于定预测时域控制器。在目标车速5 km／h下，对于与预测时域参数关联度最高的横摆角偏差，定预测时域参数控制器在轨迹点上的横摆角偏差均值为9.918°，而自适应预测时域参数控制器的横摆角偏差均值为8.46°，控制精度提高了14.7%。自适应预测时域参数控制器在轨迹点上的平均横向偏差为0.307 5 m，最大纵向速度偏差为1.716 2 km／h，而定预测时域控制器的平均横向偏差为0.392 9m，最大纵向速度偏差为4.023 1 km／h，行驶过程中出现明显的纵向速度偏离期望值过大现象。这表明自适应预测时域控制器在实际控制过程中，车辆的跟踪精度和乘坐舒适性均要优于定预测时域控制器控制。