基于构网型控制策略的直驱型风力发电机简化模型研究

2024-03-19刘京波郇政林谭延博顾天明王谱宇

重庆理工大学学报(自然科学) 2024年2期

李琰，刘京波，郇政林，谭延博，顾天明，王新，王谱宇

（1.国网冀北电力有限公司电力科学研究院（华北电力科学研究院有限责任公司），北京 100045；2.南京理工大学自动化学院，南京 210094）

0 引言

随着全球对可再生能源的需求增加，我国在近年来加大了对风电等可再生能源的投资和建设［1］，促进风电场可输电能力的进一步提高［2－3］。直驱式风力发电作为当前风力发电的普遍形式，其接入电网对电力系统的稳定性具有重要影响［4］。其中永磁直驱风机具有以下优点［5］：提高风能转化为电能的效率，降低制造成本，消除机械中间件，减少摩擦磨损，增强系统的稳定性。综上，直驱风机的研究对于风力发电有着重要意义。

目前的直驱风机电磁暂态模型，大多使用包括风电机组、传动系统、发电机、变流器和控制策略的详细模型，具有精确性高的优点，但对算力要求较高，不适用于多台风机机组并网的研究。因此，亟需对详细模型进行简化，保留需要研究的并网特性，提高仿真速度。文献［6］提出一种变流器数学模型的简化方法，把变流器等效为一个受控的电能变换传递元件。文献［7］提出一种逐点消去的聚合等值方法，实现了模型的简化等值流程。文献［8］建立了一种求取等效风速的单机风电场聚合模型。文献［9］忽略了变流器电力电子器件和脉宽调制（pulse width modulation，PWM）空间矢量调制过程，实现了简化。文献［10］讨论了适用于直驱风机频率响应控制研究的风电机组模型简化方法，主要关注机电暂态模型。其根据虚拟惯量控制的物理本质，提出了直驱风机的模型简化原则，建立简化模型。通过多台风机的功率聚合等值建模方法，实现多台风机并网模型的简化。而本文主要关注风机模型在电磁暂态过程中的并网特性，从风机并网数学模型入手，简化数学模型和电磁暂态模型。文献［11］利用永磁发电机控制策略的解耦合项和永磁发电机数学模型中的耦合项抵消，电网侧变流器控制策略中的解耦合项和电网侧变流器数学模型中的耦合项抵消，即利用控制策略解耦抵消模型中的耦合项，以此建立风机模型的机电暂态模型，从而实现模型简化。而本文主要对风机电磁暂态模型进行研究，从数学模型本质上进行简化，未改变控制策略部分。文献［12］基于特征值分析法、参与因子和特征值灵敏度分析，实现模型的降阶简化。上述文献都是基于跟网型控制策略下的模型简化，且普遍采用省略替换变流器的方法来简化模型，并没有研究基于构网型控制的风机模型简化方法。

直驱风机经背靠背换流站并网的详细建模，可以全面地反映风电机组的响应特性。单台风机详细建模是目前仿真软件普遍的建模方式，然而多台机组的仿真建模会导致仿真运行环境复杂，硬件在环系统的算力无法达到仿真要求。本文针对构网型控制下的直驱风机机组详细模型进行简化，采用受控电流源替代风机机侧模型的方法，研究多台风机并网特性，从输入功率／直流电压／交流电压波动3个方面进行模型对比，从模型响应曲线误差和仿真耗时2个角度对详细模型及简化模型进行评价。

1 直驱风机系统机侧数学模型

本节首先构建详细直驱风机模型，为后续简化模型的建立提供理论建模基础。

1.1 直驱风机数学模型

传统直驱风机机组拓扑图如图1所示，主要由风力机及传动系统，永磁同步发电机（permanent magnet synchronous generator，PMSG）以及换流站组成［13］。

图1 单台直驱风机机组拓扑图

1）风力机模型

基于空气动力学原理，风力机输出的功率为［13－15］：

式中：ρ为空气密度，取1.25 kg／m3，R为叶片半径，v为风速，额定值取9 m／s，Cp为风能利用率，根据贝兹理论［13，16］，其值最大为0.593，其具体表达式为：

式中：λ为叶尖速比，c1—c8为风机特性常数，ωwt为风轮角频率，β为桨距角。由式（2）可得到风能利用系数曲线，当桨距角β增大时，风能利用系数Cp值将减小；当桨距角恒定时，随着叶尖速比λ的增大，风能利用系数先增大后减小，即存在最大风能利用系数Cpmax。

当风速低于额定风速时，风力机输出机械功率由最大功率跟踪（MPPT）控制［17］，如式（3）所示，Prated为电机额定容量；当风速高于额定风速时，其发出机械功率由桨距角控制，限制在额定功率，控制框图如图2所示。

图2 桨距角控制框图

式中：ωref为达到风机额定功率时的转子转速，在风机参数确定后，有功功率和转子转速成正比，转速上限控制功率上限；ωs为实际转速，与风轮转速的关系为ωs＝npωwt（np为极对数，直驱风机极对数较多，本文取np＝100）；Hj为桨叶的惯性常数。实际中，PI控制器中积分量和βref不能小于0，因此需要对其分别进行速率限制和幅值限制，使其大于零。

输出机械转矩模型为［13－15］：

2）传动系统模型

本文中传动模型采用单质量块模型。传动模型方程为［13，16，18］：

式中：H为直驱风机的总转动惯量，Tm为机械转矩，Te为电磁转矩。

3）永磁同步电机模型

在同步旋转坐标系下，永磁同步电机的dq轴电压方程为［13－14］：

式中：Ls、Rs分别为定子电感和电阻，uds、uqs为定子电压的d、q轴分量，ids、iqs为定子电流的d、q轴分量，ψf为永磁体的磁链幅值。

永磁同步发电机的电磁转矩动态方程为［11］：

式中：Lds、Lqs分别为d、q轴定子绕组同步电感。

1.2 直驱风机换流站数学模型

本节主要针对背靠背变流器进行建模，其拓扑如图3所示。机侧变流器输出的有功功率通过直流线路输送到网侧变流器中，实现风力发电系统中的功率传递和控制［15］。本文中采用的是电压型变流器（voltage source converter，VSC）。

图3 直驱风机详细模型拓扑图

直流侧电容电压动态模型为［13］：

式中：Pw为机侧换流器输出的有功功率，Pl为网侧换流器输入的有功功率，udg、uqg为网侧换流器出口d、q轴电压，idg、iqg为网侧换流器出口d、q轴电流，C为直流侧电容，uDC为直流侧电容电压。

1.3 机侧控制策略

机侧换流器（machine-side converter，MSC）控制发电机的转速和定子d轴电流。有功外环控制使得发电机的转速跟踪到最佳转速，实现最大输出功率跟踪［17］。同时发电机采用零d轴电流控制，取参考值idsref＝0，控制输出无功为0；控制交轴电流iq实现对转矩和输出有功的控制［13，19］。机侧换流站控制框图如图4所示。

图4 机侧换流站控制框图

双闭环控制采用PI控制器控制dq轴电流跟踪参考电流值［13，20］，并通过耦合项ωsLdsids和ωsLqsiqs及前馈项ωsψf消除耦合。控制方程如下：

式中：Kp1／Ki1为定子d轴电流内环控制比例／积分参数，Kp2／Ki2为转子转速内环控制比例／积分参数，Kp3／Ki3为转子转速外环控制比例／积分参数。ids＿ref／iqs＿ref为d／q轴电流参考值。

1.4 网侧控制策略

网侧换流器（grid-side converter，GSC）采用构网型控制（grid-forming，GFM）［21－24］，不同于跟网型控制（grid-following，GFL），其不需要锁相环（phase-locked loop，PLL）的作用［25－29］。其控制策略类似于同步发电机的功率同步过程［27－33］。本文中构网型控制策略采用直流惯性电容控制［34－35］，通过直流电容模拟同步发电机的转子惯性，控制策略如图5所示。

图5 构网型控制策略框图

控制策略如下［34－35］：

其中：ω／θ为输出角频率／相角，fn为网侧额定频率，KD为直流惯性环节控制参数，ωref为参考角频率（取为1），uDC＿ref为直流电压参考值，uDC为直流电压测量值，Em为变流器控制电压，Vac＿ref为交流电压参考值，Vac＿meas为交流电压测量值，Kpe／Kie为PI控制参数。

2 构网型直驱风机简化模型

2.1 等效简化拓扑结构

上述基于构网型控制的直驱风机详细建模，可全面反映风电机组的响应特性。然而多台机组的接入导致硬件在环系统的算力不足以达到其详细仿真要求［36］。因此需要对直驱风机机侧进行等效替代，最终得到适用于并网研究的简化模型如图6所示。

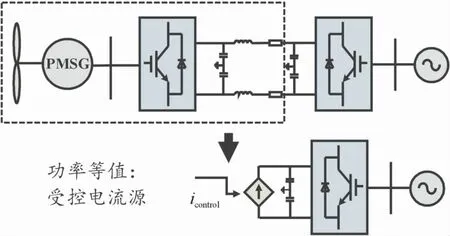
图6 直驱风机简化模型拓扑图

2.2 等效简化数学依据

该简化模型将直驱风机机侧模型输出功率特性用受控电流源代替，保留机组网侧模块，在保证一定仿真精度的同时显著提高了仿真速度。基于以下假设：风速变化时，忽略风机的惯性过程，即输出功率可以瞬时变化。受控电流源的具体表达式如下：

由式（12）可知，当网侧换流器控制uDC保持在额定值时，受控电流与风速v成正比。等效简化模型是机侧模型与网侧模型的接口，其等值为可控电流源，简化流程如图7所示。

图7 直驱风机简化流程

图7中：P为机侧输出的有功功率，icontrol为等值的受控电流源电流。机侧功率的输出特性由icontrol控制的等值受控电流源来替代，机侧风速的变化对网侧的影响可充分反映。

使用受控源代替机侧模型减少了计算量和开发成本，提高了响应速度。但由于简化模型忽略了机侧换流器，无法反映完整的机侧动态及整流逆变过程，存在一定的误差。

3 仿真分析

3.1 仿真模型

在PSCAD／EMTDC中搭建详细模型（图3）及简化模型（图6）。通过对比受扰动时详细模型和简化模型的动态特性，验证简化模型对于风机并网特性研究的有效性。仿真系统主要参数如表1所示。

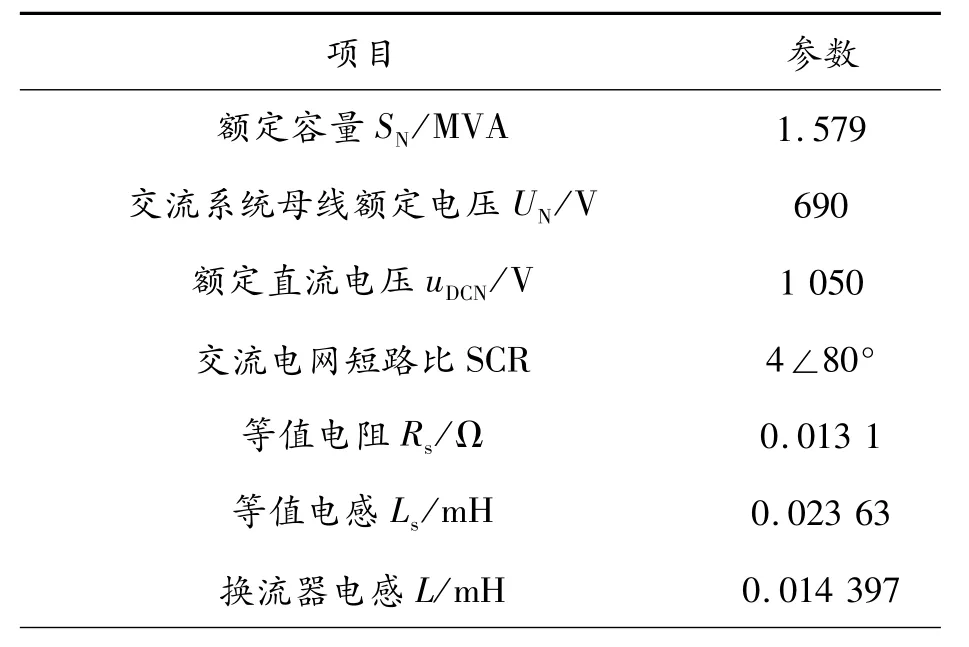
表1 仿真系统主要参数

3.2 系统模型暂态仿真分析

3.2.1 输入功率（Pmeas）变化

系统处于额定状态时，此时详细模型风速为9 m／s，对应的简化模型可控电流计算为0.418 2 kA。当系统运行至30 s时，详细模型风速波动，由9 m／s降为8 m／s，5 s后恢复正常，仿真设置时长为40 s。相应简化模型的受控电流源可控电流则降为0.293 7 kA。本文的研究对象为直驱风机并网后的网侧特性，在仿真中以网侧输入功率／直流电压／交流电压波动3个指标作为模型评价标准［37］。对比分析：

详细模型：风速变化（由9 m／s降为8 m／维持5 s）。

简化模型：可控电流变化（由0.418 2 kA降为0.293 7 kA维持5 s）。

该暂态测试的目的是验证详细模型与简化模型在并网特性研究上的一致性。仿真结果如图8所示（图中变量均为标幺值形式）。

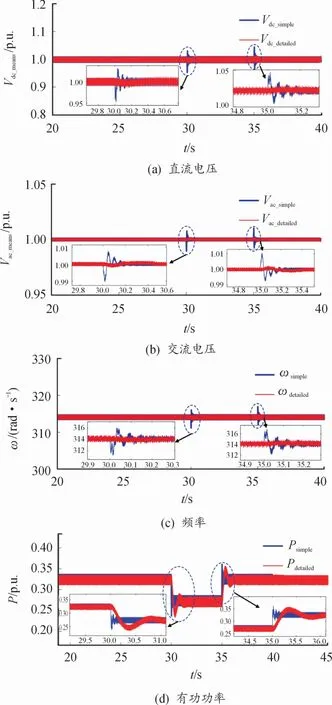
图8 输入功率变化详细／简化模型网侧输出波形

图8中：Vdc表示直流电压，Vac表示网侧交流电压，ω表示系统频率，P表示输出有功功率，下标simple表示简化模型的变量，下标detailed表示详细模型的变量。直驱风电机组详细模型和简化模型的仿真耗时如表2所示［本文所采用的PSCAD／EMTDC仿真软件版本为4.6.2，编译器为Intel（R）Visual Fortran Compiler XE 15.0.0.108（64－bit）］。

对图8进行误差分析。基于误差计算公式（13），计算得到输出波形误差分析结果，见表3。

表3 输出波形误差分析结果

式中：X代表交流电压／直流电压／频率／有功功率中的变量，Xs为简化模型中变量的波动值，max表示其最大值。Xd代表详细模型中变量的基准值。

由表2可以看出，在相同的仿真步长下，本文所提出简化模型比详细模型仿真耗时明显缩短，且随着仿真步长的减小，简化模型仿真效率提高得更明显。因此在研究直驱风电场并网时，采用本文的简化模型可大幅缩短仿真耗时，提高仿真效率。误差分析：本节的测试内容主要关注简化模型能否反映出详细模型的实际外特性曲线。由图8和表3可知，在采用受控电流源代替详细风机构建简化模型时。简化模型各参数指标能够快速跟踪其参考值。详细模型由于直驱风机的惯性作用，对于功率的阶跃有着良好的抑制作用。简化模型由于采用直流电流源等效替代机侧特性，无法对功率的阶跃实现抑制作用，但波动率均在可接受范围内。简化模型可以近似替代详细模型，在节省计算资源的基础上，简化模型也能够实现实际的并网外特性研究。

3.2.2 输入功率一致时，网侧直流电压变化

保证详细模型与简化模型网侧输入功率一致，稳态时各参数变量保持一致。详细模型中风速为9 m／s，简化模型中可控电流为0.418 2 kA。在30 s时，详细模型和简化模型网侧直流电压发生阶跃，均由1p.u.降为0.95p.u.，且维持5 s，仿真总时长为40 s。仿真结果如图9所示。