电动汽车双层优化模型的充放电调度策略

2024-03-19马永翔王希鑫闫群民孔志战淡文国

重庆理工大学学报(自然科学) 2024年2期

马永翔，王希鑫，闫群民，孔志战，淡文国

（1.陕西理工大学电气工程学院，陕西汉中 723001；2.陕西省电力有限公司，西安 710048；3.乌兰察布电业局，内蒙古乌兰察布 012000）

0 引言

电动汽车（electric vehicle）因其清洁、高效以及储能优良的特性而逐渐普及，可以有效解决当前能源短缺、环境污染的问题［1－3］。截至2023年底，全国新能源汽车保有量达2 041万辆，占汽车总量的6.07%。其中，纯电动汽车保有量1 552万辆，占新能源汽车保有量的76.04%；预计到2026年新能源汽车市占率将超过50%，占据汽车市场主导地位。然而，大量的EV无序充电会给电网带来众多棘手问题，极大地影响了电网的安全性和可靠性［4－7］。因此，合理、高效的EV充放电调度策略，是当前车网双向互动V2G（vehicle-togrid）技术要解决的核心问题。

当前，国内外EV充放电优化调度策略主要如下：文献［8－10］中都是通过传统分时电价（timeof-use tariff，TOUT）策略去引导用户在负荷低谷时期充电，在削峰填谷的同时也为用户带来利益。然而数量庞大的EV在低价时段集中充电，易形成新的负荷高峰。文献［11－13］都是以降低用户成本为目标去考虑EV的优化调度，虽然用户的成本降低且参与度提高，但是对于电网侧日负荷的削峰填谷效果不佳，仍存在负荷高峰现象。文献［14－15］运用多目标函数从电网侧和用户侧两侧的角度对EV进行控制策略，既考虑到用户的成本，又对电网侧的峰谷差有明显改善，但是由于在多目标函数加权到总目标函数的过程中，权重系数很难取到最佳值，导致两侧的优化很难都达到预期效果；文献［16－18］对两侧分别进行优化调度，欲使其在日负荷峰谷差降低的同时减少用户成本，提高用户的参与度，但上述文献仅使用MATLAB平台YALMIP工具箱中的求解器进行求解，在面对数量庞大的EV时，求解精度明显欠佳。

上述文献所采用的EV优化调度策略，虽然考虑了电网和用户两侧的需求，但存在着出现新的负荷高峰、削峰填谷效果不佳、用户参与度不高和算法求解精度欠佳等问题。针对上述问题，提出一种基于电网和用户两侧需求的V2G双层优化调度策略。首先，第1层模型以电网日负荷方差最小为目标函数；第2层优化模型建立以车主充电成本最小以及保证用户出行需求的多目标函数，然后利用改进的粒子群-模拟退火算法依次对双层优化模型进行循环迭代求解，并将第2层优化后的结果反馈给第1层，以此循环优化，输出最终优化调度安排，实现EV的优化调度。最后，通过对当前各优化调度策略的仿真算例分析，对比验证所提策略的优越性。

1 电动汽车优化调度控制架构

本文采用的分层式调度控制包含3层结构：配电网调度层、充电站运营层（控制层）和用户层，如图1所示。

图1 电动汽车优化调度控制架构

3层之间通过完善的通信网络拥有实时的信息交互。配电网调度层拥有控制各充电站任意时段的充放电负荷的调度程序和检验电压、电流等约束是否越界的潮流计算程序［19］。充电站运营层（控制层），一方面为入站的EV提供充放电方案，另一方面将待充放电的车辆信息传输给调度中心并接受优化调度。智能充电装置作为终端设备，可以对EV充电、放电、空闲3种状态进行充放电控制［20］。经过信息的交互和调度中心的优化调度方案，由充电站运营层（控制层）将最终的调度计划发送给各智能充电装置，并开始充放电。

2 电动汽车充放电双层优化调度模型

2.1 电动汽车充电负荷的时间分布预测

EV是否需要充电主要由其行驶里程决定。一般电动私家车用户结束一天的行程回家后就连接充电装置，这个时间对应EV的结束行程时间；车主次日出门时间即离开充电装置的时间对应EV开始行程时间。根据EV的行为特性研究，通过拟合可以得到EV的日行驶里程、起始和结束充电时间的概率密度函数［21］。

EV日行驶里程为对数正态分布，其概率密度函数如式（1）所示。

式中：σ、μ分别是标准差和期望值。μ＝3.7，σ＝0.92。

EV的起始、结束充电时间的函数如式（2）和式（3）所示。

其中，σ、μ分别是标准差和期望值；t表示起始的充电时刻。μs＝17.5；σs＝3.5；μe＝9.24。

结合EV用户的出行特性，可以计算调度EVi充电所需时长Ti，c，如式（4）所示。

式中：Sc，i、S0，i分别是车主EVi期望SOC（state of charge）和起始SOC；Ci表示EVi的电池容量；Pi，c、Ec分别表示EVi的充电功率和充电效率。

基于蒙特卡洛法可以得到各EV的充电具体时间段，从而得到该地区配电网各时段的总负荷，预测流程如下：

1）基础参数设置，在该地区配电网中保有1 500辆EV，其电池容量为35 kW·h，平均每百公里耗电为20 kW·h；充电功率为7 kW，效率为90%；以重庆市居民分时电价作为EV充电的峰谷电价标准，无序充电的固定电价为上述峰平谷电价的平均值0.513元／（kW·h），如表1所示。

表1 重庆市电动汽车充放电的分时电价

2）依据EV的概率密度函数，用蒙特卡洛法随机抽样，计算EV到家的初始SOC及每个EV充电的开始、结束的时间，并以此计算单辆EV的充电负荷。

3）用蒙特卡洛法对EV进行随机抽样，将各时段内的EV充电功率叠加，当抽样的次数与EV数量相等时，抽样结束，即可得到EV在t时刻总充电负荷。

4）将每个小时平均离散化为4段，每个时段为15 min，一天共分为96个时间段。将取得的数据按照t＝1，2，3，…，96的时间间隔排序，绘制电网总日负荷曲线如图2所示。

图2 电动汽车各种充电情况下的电网总负荷曲线

仿真结果表明：随着大量的EV接入配电网，无序充电负荷将对配电网的安全运行带来巨大冲击，负荷曲线在18∶00—21∶00之间产生负荷高峰；在凌晨24∶00—4∶00时电网负荷进入低谷期，并且随着EV数目的增加，电网总负荷峰谷差不断加大。根据分时电价引导的负荷曲线虽在晚间18∶00—21∶00有一定的削峰效果，但是效果欠佳，且在10∶15—次日3∶00时段产生了新的负荷高峰。针对上述的问题，在充分考虑电网和用户两侧需求的情况下，提出一种基于双层优化模型的充放电调度策略，以此来降低分时电价所产生的新的负荷高峰和峰谷差。

2.2 第1层电动汽车优化模型

通过EVi在各时间段内的充放电功率为控制变量，V2G优化调度策略在电网侧主要以削峰填谷为目标，建立日负荷方差最小的目标函数如式（5）和式（6）所示。

式中：PLt、Pav分别表示t时段的负荷功率以及平均负荷功率，kW。n为EV数量；Pit的正、负值表示EVi在t时段的放电和充电的功率。

2.3 第2层电动汽车优化模型

电池循环充放电导致电池退化所产生的额外成本应当考虑。文献［22］中EV电池退化成本如式（7）所示，电池循环次数与使用寿命的关系曲线如图3所示。

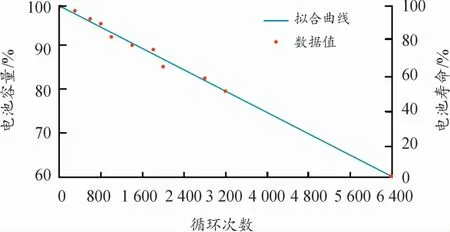
图3 纳米磷酸铁锂电池循环次数-寿命曲线

式中：Ci，t、χk，t分别表示EVi在t时段的电池退化成本，元和循环充放电电量，kW·h；Bi、CB分别表示电池寿命与循环次数两者的线性关系系数，即图3中拟合曲线斜率和电池更换成本，元；Si，t、Si，t－1分别表示EVi在t时段和t－1时段的SOC。

在第1层优化充放电方案的基础上进行第2层优化，根据分时电价，V2G会给用户带来差价收益，以车主充放电成本最小为目标，构造车主充放电成本最低的目标函数如式（8）所示。

式中：S1i、S2i分别表示充、放电参数，充电时S1i＝1，S2i＝0；放电时S1i＝0，S2i＝1；未充、放电时S1i＝0，S2i＝0；pct、pdt分别表示t时段的充、放电电价，元／（kW·h）；Δt为单位控制时间段长度；Ec和Ed表示车载电池的充电、放电效率，此处取0.9；Ci，t为EV放电行为而导致电池损耗的成本，元。

基于用户的出行需求，以EV充放电完成后的SOC最多为目标函数，如式（9）所示。

式中：S0，i为第i辆车的初始SOC，Ci为第i辆车的电池容量。

将目标函数f21、f22进行线性加权处理［23－24］得：

式中：f2为车辆EVi的多目标函数；λ1、λ2为函数f11、f22的加权系数。、为函数f11、f22的最大值；。

2.4 双层优化模型的约束条件

V2G基于双层模型的调度策略主要有如下条件约束：

1）可用时间约束

EV绝大多数时间都处于闲停状态，但EV一天96个时间段不可能都处于并网状态，所以EV的可接受调度时间约束范围为：

式中：tV2G，i为车辆EVi参与有序充放电的可用于调度的时间。

2）EV荷电状态值约束如式（12）所示。

式中：Smax、Smin分别表示正常荷电状态的上、下限，Smax＝1，Smin＝0.3。

3）充放电功率约束

EV交换功率并非任意连续可调且需要在合理的功率范围内进行充放电［25］，由此充放电功率的范围为：

式中：Pcmax、Pdmax分别为EV最大充电、放电功率。

4）分时电价上下限约束

考虑到运营商、车主对于充电成本的承受能力，设定充放电分时电价的上下限如式（14）所示。

式中：Ptmin、Ptmax为第t时段充电电价的上、下限值，元／（kW·h）。

5）变压器容量约束

一天当中的任意时段，都要保证变压器能够合理正常运行［26］。

式中：Pload，t、ST分别表示该时段的基础负荷以及变压器容量限值。

2.5 双层模型的优化流程

1）优化调度前控制中心需对EV能否参与调度进行信息采集和筛选。将可参与调度的EV的信息交给决策中心进行优化调度。与此同时，采集电网负荷及电价等信息。

2）通过控制一天内EV不同时间段充放电功率，考虑变压器以及EV充放电功率等多方面约束对第1层模型进行优化计算，得到仅考虑电网侧需求的日负荷曲线。

3）以第一阶段优化结果作为约束，进行基于用户侧需求的第2层优化策略。以车主充放电成本最小为优化目标，并考虑该层模型多方面的约束条件进行优化计算，得到第2层模型的优化结果。

4）将第2层模型得到的各时间段EV的充放电功率优化结果Pi，t反馈给上层进行下一轮循环，通过上下层模型反复迭代至结果满足终止条件，此时跳出循环，得到基于双层模型的电动汽车优化调度的最优解。

5）将最终的优化结果反馈至智能充电装置中，并由智能充电装置和其下配合的EV执行策略优化后的调度安排。

3 算法介绍及其求解流程

3.1 改进的粒子群-模拟退火算法

考虑到本文所建EV双层优化模型的特点以及PSO、SA算法的优劣势，对标准的PSO算法进行改进，引入较小的惯性权重，以此来加快粒子的局部寻优过程，然后运用SA算法对当前PSO所得的最优解进行扰动、寻优，试图跳出局部最优，搜索更优的解。应用改进的PSO-SA混合算法对双层模型进行求解，解决PSO算法易陷入局部最优解的问题以及SA算法收敛速度慢的问题，同时发挥2种算法的优势。

改进的PSO-SA算法流程如图4所示。

图4 改进的PSO-SA算法流程框图

具体求解流程如下：

1）初始化粒子的位置和速度即EV在不同时间段的充放电功率。

2）引入较小的惯性权重计算当前粒子的适应值得到当前的峰谷差和车主充放电成本。

3）并根据每次迭代结果更新局部、全局最优值，pbest、gbest。

4）达到迭代次数或满足终止条件则跳出循环得到由改进PSO算法求得的最优解。

5）由此最优解作为SA算法的初解进行扰动，并根据Metropolis准则接受新解，以此来试图寻求更优解。达到迭代次数或满足终止条件则跳出循环得到最终的最优解和结果。

3.2 算法对比

为了验证本文所改进算法的可行性，分别用PSO、SA、PSO-SA这3种算法对上述模型进行求解，结果如图5所示。

图5 各算法收敛结果曲线

由图5可知，PSO算法虽迭代436次就达到最优，收敛速度最快，但明显陷入局部最优。SA算法所得解虽明显比PSO最优解更佳，但是收敛速度却大大变慢，在840次才达到最优。而PSO-SA算法对比PSO算法虽迭代次数增加到612次，但是最优解却达到最佳；对比SA算法，其收敛速度和最优解都明显更佳。综上所述，本文所用PSOSA具有高效性和更好的寻优精度，优化效果更佳。

4 仿真算例对比分析

4.1 仿真算例参数设置

根据当前国内EV的实际情况以及众多影响因素，本文以重庆某地区参数为例在Matlab平台进行仿真验证：

1）智能充电装置可以对EV充放电状态进行控制并由4台功率因数为0.85、容量为1 600 kV·A的变压器供电，其效率为95%。

2）在该地区配电网中保有1 500辆EV，其电池容量设置为35 kW·h，平均百公里耗电20 kW·h；充、放电功率为7 kW，效率为90%。

3）EV每天充电1次，且结束充放电时电池电能满足用户基本需求，电池的更换成本为CB＝40 000元。

4）峰平谷电价信息以重庆市EV充放电的分时电价为参考，具体见表1所示。

4.2 仿真算例结果

运用蒙特卡洛法仿真1 500辆EV在96个时间段内的充放电情况，并以电网和用户两侧的目标函数建立多目标模型以及本文所研究的双层模型进行V2G优化调度。然后利用改进的PSO-SA算法对2种策略分别进行优化求解，所得仿真结果如图6和图7所示。由图6可知，多目标的优化调度策略在18∶00—21∶00负荷高峰期间有削峰作用。但在多目标函数加权到总目标函数的过程中，权重系数很难取到最佳值，导致两侧的优化很难都达到预期效果，使得削峰填谷作用效果欠佳。因此，需要用双层模型调度策略进行改善。

图6 多目标优化调度的负荷曲线

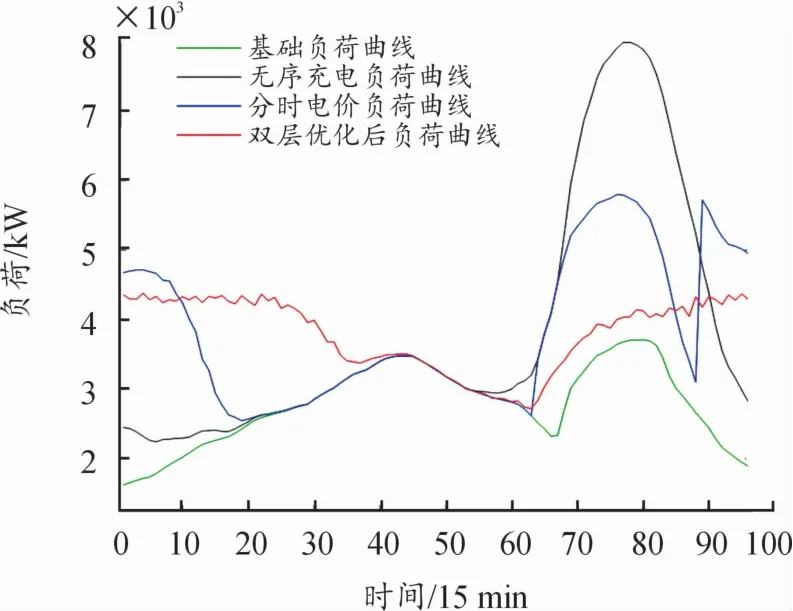
图7 双层模型优化调度的负荷曲线

基于以上分时电价和多目标优化调度策略存在的问题，例如易出现新的负荷高峰以及日负荷曲线削峰填谷效果欠佳。本文在考虑各种约束条件的情况下，采用双层模型对EV有序充放电进行优化调度，输出最终结果如图7所示。由图7可知，双层模型优化调度策略大大降低了新的负荷高峰和负荷峰谷差。

4.3 数据对比分析

经上述的仿真计算，通过无序充电、分时电价充电、多目标模型优化调度及本文的双层模型优化调度策略4种结果，得到具体的日负荷峰谷值对比和车主充电成本对比，如表2和表3所示。分别对日负荷曲线峰谷差、日负荷曲线均方差以及车主的充放电成本进行对比。

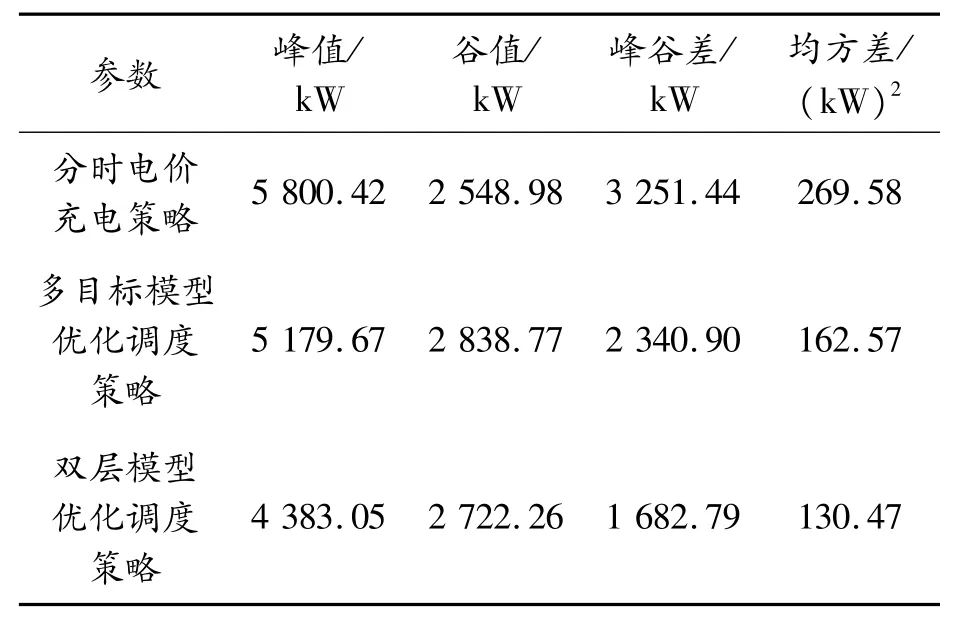
表2 日负荷峰谷值

表3 车主充电成本

由表2可知，多目标模型优化策略相较于分时电价充电策略的峰谷差仅下降28.11%；双层优化策略相较于分时电价策略峰谷差下降48.24%，且在新的负荷高峰处下降24.39%；双层模型调度策略相较于多目标模型调度策略的峰谷差仍下降28%。通过上述峰谷差对比分析可知，双层模型优化调度策略有更好的削峰填谷效果，且大大降低了新的负荷高峰。在日负荷均方差方面，多目标模型优化策略对比分时电价充电策略下降了39.7%；双层优化策略对比分时电价策略下降了51.6%，相较于多目标模型下降了19.75%。由此可知双层模型优化调度策略相较于其他2种优化策略，日负荷方差明显降低，电网的稳定性大大提升。

在车主充放电成本方面，由表3可知，采用多目标模型和双层模型优化调度策略的车主，充放电成本与无序充电成本相比，分别下降17.02%和24.63%，双层模型相较多目标模型优化调度EV充电成本仍有减少，为9.18%。采用本文中所提出的双层模型优化策略，相较于无序充电和多目标模型优化调度策略车主，成本降低明显，提高了车主对V2G优化调度的参与意愿。