离轴拖挂轮式移动机器人跟踪控制研究
2024-03-19苗盛阳周宇生
苗盛阳,周宇生
(贵州大学数学与统计学院,贵阳 550025)
0 引言
轮式移动机器人是通过车轮转动完成运动任务的一类特殊的移动机器人,具有结构简单、运动灵活和能耗低等优点,广泛应用于工业物料运输和医疗等领域[1-3]。在众多的轮式移动机器人中,有一类被称为拖挂轮式移动机器人,它由多个单体轮式移动机器人连接而成[4-5]。根据相邻2个移动机器人连接方式的不同,拖挂轮式移动机器人可分为轴上拖挂轮式移动机器人和离轴拖挂轮式移动机器人。轴上拖挂轮式移动机器人中相邻两车的连接点位于前车轮轴的中点[6-7],而离轴拖挂轮式移动机器人中相邻两车的连接点位于前车尾杆的末端[8-11]。
轨迹跟踪控制问题是拖挂轮式移动机器人控制中的一类重要问题,但复杂的结构、严重的欠驱动特性和非完整约束的影响,给拖挂轮式移动机器人的运动控制带来了极大的困难[12-13]。针对轴上拖挂轮式移动机器人中挂车的轨迹跟踪控制问题,文献[14]基于李雅普诺夫函数设计了速度控制器,实现了挂车的位置跟踪。针对轴上拖挂轮式移动机器人中拖车和挂车沿相同轨迹运动控制问题,文献[15]通过增加控制输入实现了对挂车的控制,并通过李雅普诺夫直接法设计了一种运动学控制器,实现了拖车和挂车沿同一轨迹运动。上述仅仅基于运动学模型设计控制器的方法虽然能实现轨迹跟踪,但是没有考虑机械系统的动力学模型,忽略了速度变化。而速度控制一般是通过力矩控制器来实现的,因此在控制设计过程中还要考虑动力学模型。动力学模型是描述速度与控制输入力矩的变化关系的模型,可采用基于机械系统能量的欧拉-拉格朗日方程进行推导[16-17]。为了实现更加有效的控制,同时考虑位置跟踪和速度跟踪的双环控制方法受到越来越多学者的青睐。双环控制方法由内环和外环2个控制器组成,该方法可将不同的控制方法结合起来,充分发挥不同控制方法的优点。如文献[16]提出了一种由模型预测控制方法和滑模控制方法相结合的双环控制方法,该方法将模型预测控制的预测功能和滑模控制的鲁棒性有机结合起来,实现了挂车精确的轨迹跟踪。文献[18]提出了一种由基于李雅普诺夫函数的速度控制器和自适应力矩控制器组成的双环控制方法,该方法在具有不确定因素的情况下实现了挂车的轨迹跟踪控制。双环控制方法虽然能实现控制目标,但为拖挂轮式移动机器人同时设计出2个合适的控制方法不是一件简单的事情,并且上述研究忽视了移动机器人的潜在运动规律,难以精确地实现运动控制。想要实现拖挂轮式移动机器人的精确轨迹跟踪,应充分挖掘潜在的运动规律,并将运动规律和控制器的设计有效地结合起来。如文献[19]提出了一种动态轨迹跟踪方法,该方法的核心是引入以目标轨迹曲线弧长来表示的相对曲率,通过跟踪目标轨迹曲线的相对曲率来实现对轨迹的精确跟踪。此外,对于轴上拖挂轮式移动机器人中挂车的轨迹控制问题,文献[20]给出了两车的运动轨迹曲线相对曲率的关系,并通过最优控制和滑模控制方法同时实现了拖车和挂车的运动控制。由于非完整约束的影响,拖车和挂车很难沿着同一轨迹运动。为了实现拖车和挂车沿同一轨迹运动,文献[21]为轴上拖挂轮式移动机器人中的挂车增添1个被动操舵角,在此基础上推导出了拖车和挂车之间的速度关系,通过动态跟踪方法实现了拖车和挂车沿同一轨迹运动。
然而上述结合运动规律的控制方法都是针对轴上拖挂轮式移动机器人提出的。与轴上拖挂轮式移动机器人相比,离轴拖挂轮式移动机器人的前车尾部有一段额外的连杆,后车与前车的连接点在上述连杆的末端,而轴上拖挂轮式移动机器人后车与前车的连接点在前车轮轴的中心,可以说轴上拖挂轮式移动机器人是离轴拖挂轮式移动机器人的一种特殊情形(即前车尾端连杆长度为零)。因此,离轴拖挂模型比轴上拖挂模型复杂,且由于连接点离前车的中心有一定的距离,使得其运动规律也更加复杂。上述2个原因导致离轴拖挂轮式移动机器人运动规律的相关研究较少。针对离轴拖挂轮式移动机器人中挂车的轨迹跟踪控制问题,研究给出了拖车和挂车的运动轨迹满足的一个重要的曲率关系,利用此关系将挂车的轨迹跟踪问题转化为拖车的轨迹跟踪问题,并利用动态跟踪方法设计出比例积分反馈控制器,实现了挂车的精确轨迹跟踪。
1 问题描述
下面将介绍离轴拖挂轮式移动机器人的结构及其运动学和动力学模型。
1.1 结构介绍
如图1所示,离轴拖挂轮式移动机器人由前面的拖车、中间的刚体连杆以及跟在后面的挂车组成。通常情况下,拖车含有2个主动的驱动轮和1个被动的万向轮。拖车在驱动轮的转动下实现自主移动,挂车一般不含驱动装置,只能在拖车的拉拽下完成运动。为了方便起见,将拖车中左右2个驱动轮的控制输入力矩分别记作τl、τr;设拖车的质心为点A,坐标为(x1,y1),挂车的质心为点B,坐标为(x2,y2);两杆的连接点为点C,坐标为(x3,y3)。拖车的运动方向与X轴正方向的夹角为θ1,挂车的运动方向与X轴正方向的夹角为θ2。离轴拖挂轮式移动机器人的广义坐标为q=[x1,y1,θ1,θ2]T,所以离轴拖挂轮式移动机器人是1个4自由度2输入的欠驱动系统。控制目标是在拖车上施加合适的控制输入,在拖车的拖拽作用下实现挂车跟踪目标轨迹曲线。此外,研究所使用的状态变量如表1所示。

表1 模型的主要参数

图1 离轴拖挂轮式移动机器人示意图
1.2 运动学模型
将V=[v1,w1]T看作离轴拖挂轮式移动机器人的输入向量,其中v1表示拖车的前向速度,w1表示拖车的偏航转速。同时,用v2表示挂车的前向速度,w2表示挂车的偏航转速。假设离轴拖挂轮式移动机器人在运动过程中车轮不发生侧滑,则A点和B点的横向速度为零,得到的非完整约束为:
式(1)可写成矩阵的形式:
其中,
并且,A点和B点的前向速度可表示为:
结合式(1)和式(3)可得:
此外,A点和B点的位置关系可表示为
对式(6)进行关于时间t的求导,可得:
结合式(4)、式(5)、式(7)可得:
综上所述,得到的运动学方程为:
该运动学方程也可用矩阵表示为:
其中,
根据上述分析,可进一步得到:
1.3 动力学模型
为了利用欧拉-拉格朗日方程计算动力学方程,应计算出机械系统各个部分的能量。假设离轴拖挂轮式移动机器人始终在平坦地面运动,可忽略系统的势能,因此系统的总能量等于总动能。首先计算出2段连杆的总能量,假设连杆为轻质刚体连杆,质量忽略不计,则连杆的总能量为K1=0。
其次,拖车车身及其车轮的总能量可表示为:
此外,根据式(6),挂车车身及其车轮的总能量可表示为:
因此,拉格朗日函数L就可写为3部分能量的总和:
其具体表达式为:
根据非完整机械系统的欧拉-拉格朗日方程,离轴拖挂轮式移动机器人的动力学方程可写成:
按照状态变量的各阶导数,可将欧拉-拉格朗日方程进一步整理成:
式中:M(q)为惯性矩阵;C为柯氏力矩阵;T为控制输入力矩;X(q)为控制输入力矩矩阵;λ为拉格朗日乘子。
其中,
由于机械系统在运动过程中不可避免地会受到外界环境干扰D1的影响,因此在式(21)等号两边同乘ST(q)可得:
矩阵M1、C1、T1、D1的具体形式如下:
2 运动规律
在控制过程中,离轴拖挂轮式移动机器人的自由度有4个,而控制输入只有来自拖车车轮的2个控制输入力矩,这给离轴拖挂轮式移动机器人的控制带来了困难。若能找出拖车和挂车满足的运动规律,则可通过设计控制器来实现拖车的控制,并根据两车满足的运动规律间接地实现对挂车的控制。
定理1:两车的前向速度和偏航转速满足如下关系。
证明:根据几何关系,A、B、C3点的坐标满足如下的关系。
求式(32)两式的平方和,可得:
所以拖车的前向速度v1可表示为:
当刚体连杆绕着某点转动时,刚体连杆上的每一点的角速度都是相等的,但线速度不相等,线速度会随着该点与转动中心的距离的不同而不同。如图1所示,由于离轴拖挂轮式移动机器人的两杆是刚体连杆,运动时同一杆上的任意2点的偏航角和偏航转速相等,因此A点和C点的偏航角满足θ1=θ3。根据文献[20]给出的轴上拖挂轮式移动机器人拖车和挂车偏航转速关系可得:
所以拖车和挂车的速度之间的关系满足:
由式(36)可知,拖车的前向速度和偏航转速可由挂车的前向速度和偏航转速得到,但根据式(36)很难把v2、w2的具体表达式反解出来,所以结合运动学方程,将w2代入式(33)可得:
因此,拖车与挂车之间的速度关系还可表示为:
定理2:拖车运动轨迹的相对曲率k1和挂车运动轨迹的相对曲率k2满足如下的关系。
证明:结合式(34)和式(35)可得,
式中:k1和k2分别为拖车和挂车的运动轨迹曲线的相对曲率。根据式(39),可将相对曲率为k2的挂车运动轨迹转化为相对曲率为k1的拖车运动轨迹,因此挂车的轨迹跟踪控制问题可转化为拖车的轨迹跟踪控制问题。换言之,要实现挂车精确地跟踪相对曲率为k2的轨迹曲线,只需要设计2个控制输入力矩。
3 动态跟踪方法和控制器设计
下面将介绍动态跟踪方法以及控制器的设计过程,具体的控制流程如图2所示。

图2 控制流程图
3.1 动态跟踪方法
若r1=(x1r,y1r)是拖车的运动轨迹跟踪目标,则根据运动学方程可得:
对式(41)进行关于t的求导,可得:
结合式(41)和式(42)可得:
所以,拖车的速度跟踪目标(v1r,w1r)和轨迹跟踪目标(x1r,y1r)满足:
式中:k1r(s(t))为目标轨迹曲线的相对曲率,并且为轨迹曲线的弧长,并且
根据式(41)和式(44)可得,拖车的前向速度目标v1r和偏航转速目标w1r可由拖车的轨迹跟踪目标(x1r,y1r)确定;反之,轨迹跟踪目标(x1r,y1r)可由前向速度目标v1r和偏航转速目标w1r得到。对于挂车的运动轨迹跟踪目标r2=(x2r,y2r),同样可得到相似的结论:
因此,利用式(45)可将轨迹跟踪目标r2=(x2r,y2r)转化为速度跟踪目标(v2r,w2r),并利用文献[19]提出的动态跟踪方法,将前向速度目标设计为一个合适的函数,即:
式中:l为目标轨迹曲线的长度;β为合适的参数,该参数可根据实际需要进行调整。偏航转速目标通过以弧长表示的目标轨迹曲线相对曲率和前向速度的乘积得到,具体形式如下:
式中:k2r(s(t))为目标轨迹曲线的相对曲率。
3.2 控制器设计
与轴上拖挂轮式移动机器人相比,离轴拖挂轮式移动机器人的动力学模型更复杂,为了实现更精确的速度跟踪,可采用比例积分反馈控制方法。基于动力学方程(22),设计比例积分反馈控制器来实现速度跟踪。控制器可写成下面的形式:
式中:KP和KI分别为比例项矩阵和积分项矩阵,它们都是正定的常值矩阵;Kt为鲁棒项矩阵;Ve=Vc-V。将式(48)代入式(22),可得:
基于上述分析,构造的李雅普诺夫函数V为:
根据M1和KI的正定性,可得V也是正定的,再对V进行关于时间t的求导,可进一步得到:
根据李雅普诺夫稳定性理论,V≥0,≤0,因此系统是稳定的。
4 数值仿真
为了验证所提控制方法的有效性,利用Matlab进行仿真实验。根据式(22)可得,当拖车的运动轨迹是半径为的圆时,挂车的运动轨迹是1个单位圆。换言之,要实现挂车跟踪目标轨迹曲线r2=(cost,sint),仅需要控制拖车跟踪曲线根据上述的分析,当L1<L2时,拖车的运动轨迹为1个半径大于1的圆轨迹;当L1=L2时,拖车与挂车沿同一单位圆运动;当L1>L2时,拖车的运动轨迹为1个半径小于1的圆轨迹。因此,利用动态跟踪方法,将动态跟踪目标设计为:
其中,k1r(s(t))可表示为:
此外,离轴拖挂轮式移动机器人及其相关的参数取值为:r=0.05 m,β=0.5,m1=2 kg,l=2πm2=1.5 kg,mw=0.2 kg,b=0.2 m,Iw=0.01 kgm2,I1=0.1 kgm2,I2=0.05 kgm2,比例项矩阵KP=10I2,积分项矩阵KI=10I2,鲁棒项矩阵Kt=0.5I2,其中I2为二阶单位矩阵。在仿真过程中,总仿真时间设定为20 s。由于离轴拖挂轮式移动机器人在实际环境下运动的过程中不可避免地会受到外界干扰,因此外界干扰选为(td1,td2)=(0.1sint,0.1cost)。离轴拖挂轮式移动机器人前后两杆的长度是控制过程中的重要参数,会直接影响到拖车和挂车的运动轨迹。当L1<L2时,两杆的长度选择为L1=0.1m,L2=0.6 m;当L1>L2时,两杆的长度选择为L1=0.5 m,L2=0.3 m;当L1=L2时,两杆的长度选择为L1=0.3 m,L2=0.3 m。
3种情况下离轴拖挂轮式移动机器人的轨迹跟踪情况如图3—图5所示,其中黑色实线表示目标轨迹曲线,红色虚线表示拖车的运动轨迹曲线,绿色虚线表示挂车的运动轨迹曲线。可看出,挂车可沿目标轨迹运动。

图3 挂车的轨迹跟踪(L1=0.1 m,L2=0.6 m)
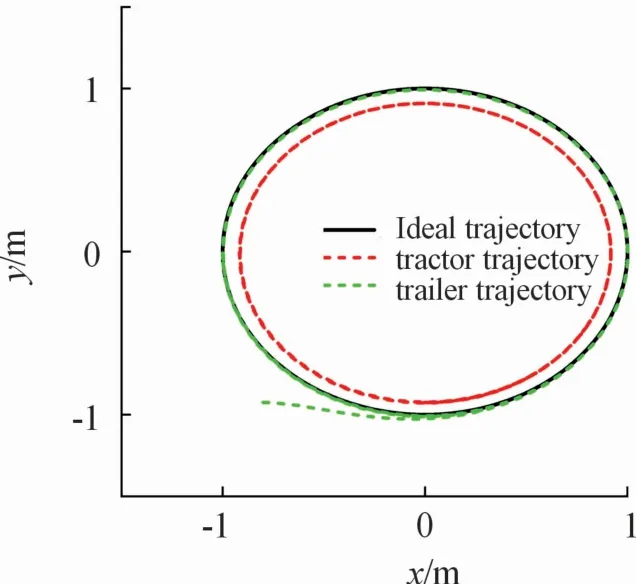
图4 挂车的轨迹跟踪(L1=0.5 m,L2=0.3 m)

图5 挂车的轨迹跟踪(L1=0.3 m,L2=0.3 m)
同时,为验证所提力矩控制器的有效性,3种情况下拖车的前向速度跟踪误差v1e和偏航转速跟踪误差w1e随时间变化的仿真结果如图6—图11所示。可看出,拖车的前向速度跟踪误差v1e和偏航转速跟踪误差w1e始终在零值附近的微小范围内变化。特别是偏航转速跟踪误差,始终在-0.02~0.02 rad/s的微小范围内变化。

图6 拖车的前向速度跟踪误差(L1=0.1 m,L2=0.6 m)
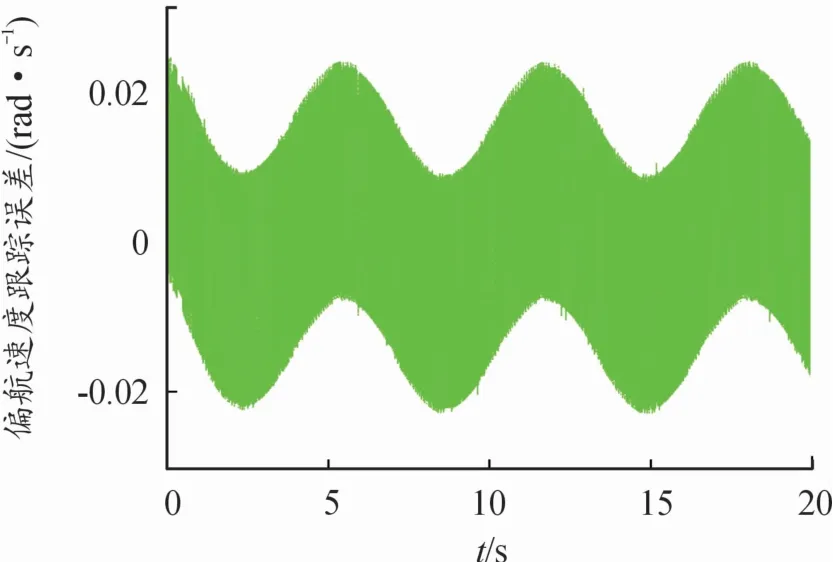
图7 拖车的偏航转速跟踪误差(L1=0.1 m,L2=0.6 m)
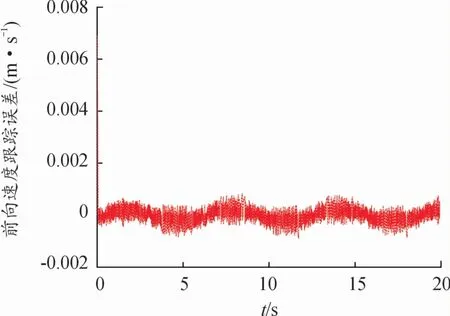
图8 拖车的前向速度跟踪误差(L1=0.5 m,L2=0.3 m)
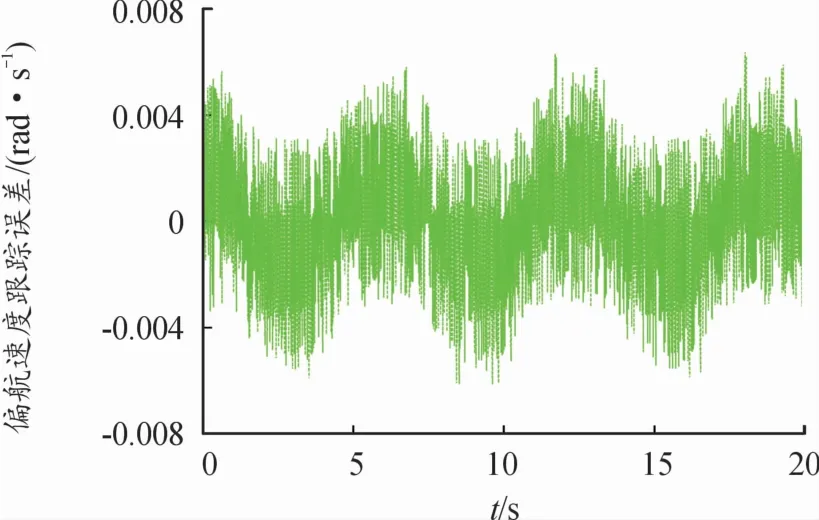
图9 拖车的偏航速度跟踪误差(L1=0.5 m,L2=0.3 m)

图10 拖车的前向速度跟踪误差(L1=0.3 m,L2=0.3 m)
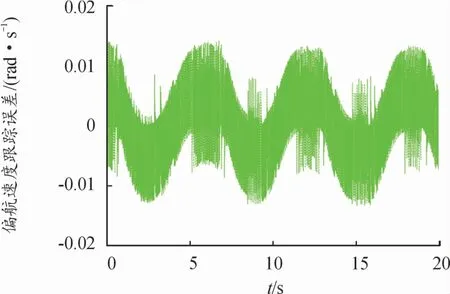
图11 拖车的偏航速度跟踪误差(L1=0.3 m,L2=0.3 m)
从理论上来讲,由于偏航转速误差始终稳定在一个趋近于零的小范围内,表明所提控制策略对目标轨迹曲线的相对曲率跟踪误差非常小,挂车可很好地跟踪目标轨迹曲线。从图3—图5也可看出,3种情况下的挂车在拖车的拉拽下可精确地跟踪目标轨迹曲线,其运动轨迹与目标轨迹几乎重合。
5 结论
1)在轴上拖挂轮式移动机器人运动规律的基础上给出了拖车和挂车之间的速度关系以及两车运动轨迹曲线的相对曲率之间的关系,将挂车的控制问题转化为拖车的控制问题,极大地降低了控制器的设计难度。
2)运用动态跟踪方法跟踪了目标轨迹曲线的相对曲率,大大增加了轨迹跟踪的精确性。
3)通过设计作用在拖车上的2个控制输入力矩实现了挂车的控制。
4)所提比例积分反馈控制器可同时实现前向速度和偏航转速的控制,为移动机器人的动力学控制器设计提供了一种新的思路。
