模糊自适应PID对保险粉合成pH值的控制研究

林志树，李洪毅，朱冠华

（1.厦门理工学院机械与汽车工程学院，福建 厦门 361024；2.广东石油化工学院广东省石化装备故障诊断重点实验室，广东 茂名 525000）

0 引言

保险粉化学名为连二亚硫酸钠（Na2S2O4），是一种呈白色或淡黄色粉末状的化工原料，被广泛地应用于纺织工业中，用于纺织物的染色、清洗、印花和脱色，还可以作为丝、毛、尼龙等织物的漂白剂，织物经漂白后色泽鲜艳，不容易退色［1］。在保险粉的合成反应中，主要工艺参数包括pH值、反应温度、压力、反应时间、搅拌强度等。其中pH值是影响保险粉合成产量和品质的关键参数，其控制过程呈现出严重的非线性、时滞性、不确定性［2］，是整个合成反应控制过程中面临的难题。目前保险粉合成反应pH值调控中，主要采用的是“常规PID＋人工干预”的方式。常规PID控制器具有结构简单、计算量小、实时性好、易于实现等优点［3］，被广泛地应用于各种工业控制中，但常规PID控制器在控制过程中使用的是一组固定参数，对于像pH值控制这种存在众多干扰因素的控制对象，其控制往往难以达到预期效果。保险粉合成过程的pH值控制还依赖于人工干预，调试人员往往根据其掌握的经验来调整药剂的投放量，确保生产过程pH值保持稳定，但这种人为控制的方式不具有科学性，同时生产效率低，与实际生产所需的快速、高效的目标不相匹配。因此，本文中提出用模糊自适应PID的方法对保险粉合成过程的pH值进行控制，在常规PID控制基础及无需人工干预条件下，利用模糊控制解决常规PID控制器参数无法自整定的问题，并结合Matlab对控制效果进行仿真分析，实现了对pH 值良好的控制效果。

1 保险粉合成原理及反应方程式

1.1 合成原理

生产保险粉所使用的方法叫甲酸钠法［4］，即用过量约10%的甲酸钠（HCOONa）、二氧化硫（SO2）-甲醇（CH3OH）溶液、焦亚硫酸钠（Na2S2O5）、环氧乙烷（C2H4O）在质量分数为78%～81%甲醇水溶液作溶剂的反应釜内进行滴加反应，批量结晶反应生成保险粉悬浊液，合格的悬浊液再进行过滤、干燥、洗涤等工序后获得保险粉晶体。

保险粉合成反应分4个阶段进行，分别是大滴加、小滴加、保温、冷却［5］，各阶段的反应条件如表1所示。

表1 反应阶段及条件

在大滴加阶段，各反应物料以大流量的方式进入合成反应釜内进行反应，该过程甲酸钠、二氧化硫-甲醇溶液需持续加入，直至加完［5］。该阶段是反应结晶的核心过程，以下对pH值控制的讨论都是围绕此过程展开的。

1.2 反应方程式

总反应：

主反应：

副反应：

在主反应的气-液-固反应过程中，反应条件比较苛刻，所需的pH值要求为4.4～4.6，该过程加入了二氧化硫，二氧化硫与水（H2O）结合形成的亚硫酸（H2SO3）会导致溶液的pH值下降，所以需要投入过量的甲酸钠与二氧化硫、水进行充分反应，使pH值始终保持在所要求的范围。副反应中，生成的保险粉会与水发生水解反应，若pH值小于4，水解反应会加剧。综上所述，在保险粉的合成反应过程中保持稳定的pH设定值是非常重要的。

2 酸碱中和pH值控制模型

溶液中，pH值大小通常用氢离子浓度［H＋］的负对数表示［6］：

在标准温度（25℃）和压力下，pH＝7的溶液中，水的离子积常数［7］表示为

由式（1）、式（2）可计算出已知pH值的溶液中氢氧根离子的浓度为

结合式（1）、式（3），求得浓度差为

式中：x为浓度差；xa为氢离子浓度；xb为氢氧根离子浓度，结合式（1）—式（4），可推导出在一定温度和压力下pH值的表达式为［7］：

式（5）给出了浓度差x与pH值之间对应的函数关系，得到的函数f（x）的曲线称为酸碱中和曲线，如图1所示。

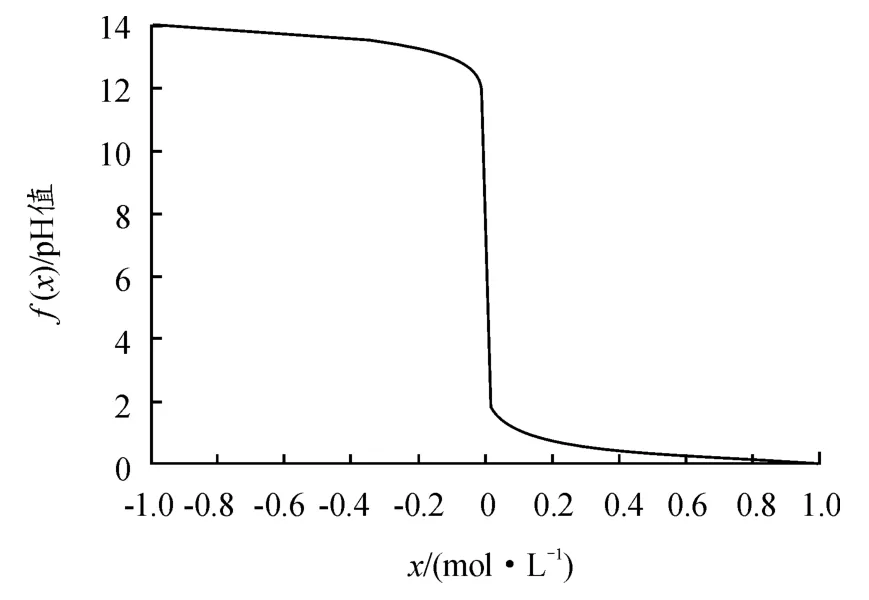
图1 酸碱中和曲线

从图1可以看出，酸碱中和过程是一个非线性、自平衡的过程，曲线形状为倒S型单调曲线，基本符合一阶惯性特征，所以反应釜内pH值控制的数学模型可用如式（6）所示的传递函数表达［8］。

式中：R为系统总增益；T为系统周期；s为系统变量；D为控制器补偿系数。

由于pH计在测量pH值时，取样时间和信号传输时间上存在滞后，因此应给系统增加一个普通滞后环节［9］，如式（7）所示。

式中：τ为滞后时间。

式（6）与式（7）间的传递关系为串联［9］，所以系统的传递函数可归结为

根据文献［10］传递函数的模型，结合实际生产情况和系统验证，式（8）各参数取值为R＝2.2、T＝80、D＝1、τ＝30，所以传递函数表达式为

3 模糊自适应PID控制器设计

随着计算机技术在工业控制领域的应用，对控制质量的要求也日益提高。但是，当需要对某些复杂的、无法建立精确数学模型的对象进行高质量控制时，还是存在一定的难度。模糊控制可以很好地解决此类问题，与传统控制不同，它不依赖被控对象的精确数学模型，可凭借操作人员的经验和专家的知识，模仿人的逻辑思维进行控制［11］。模糊控制在系统中通常不是单独作用的，与PID控制算法相结合会有更好的控制效果，因此本文中提出了模糊自适应PID控制（模糊控制＋常规PID控制）的方法对保险粉合成过程的pH值控制展开相关的研究。

模糊自适应PID控制的基本思想是将现场生产人员过去成功的经验转化为模糊控制规则，模糊控制规则能够根据实际工况实时调整PID的参数，使参数固定的常规PID控制变为能根据专家经验实时在线调整参数的变参数PID控制，以达到pH值控制效果的优化。

3.1 模糊自适应PID控制结构原理

保险粉在反应釜内合成过程的pH值的模糊自适应PID控制结构原理如图2所示。系统运行时，反应釜内pH值的偏差e和偏差变化率ec被系统实时监测，模糊控制器根据设定的模糊规则进行模糊推理和运算，得到Kp、Ki、Kd3个参数的增量值ΔKp、ΔKi、ΔKd，利用式（10）—式（12）可得出整定后Kp、Ki、Kd的值，其中K′p、K′i、K′d为PID初始设定的参数。

图2 模糊自适应PID控制结构原理图

目前PID控制普遍采用计算机技术实现，所以采用的是数字式PID算法，PID的数字形式为

式中：控制量u（k）是由模糊PID控制器调整后输出到控制变频器的电压值，变频器根据给定的电压值将其转换为对应的频率f来驱动电动机工作，电动机产生转速n，从而带动计量泵输出合适的药剂量，最终实现对保险粉合成过程pH值的稳定控制，提高产品的产量和品质。

3.2 模糊语言变量的确定

模糊自适应PID控制以pH值偏差e和偏差变化率ec作为输入变量，以ΔKp、ΔKi、ΔKd作为输出变量［12］。将这5个变量的论域均设定为（－3，3），模糊集均定义为｛NB（负大），NM（负中），NS（负小），Z（零），PS（正小），PM（正中），PB（正大）｝，其内部元素NB、NM、NS、Z、PS、PM、PB称为模糊语言值。输入量e和ec的实际变化范围均为（－0.3，0.3），因此量化因子Ke＝Kec＝3／0.3＝10；输出量ΔKp的实际变化范围为（－0.006，0.006），ΔKi、ΔKd的实际变化范围是（－0.009，0.009），因此ΔKp、ΔKi、ΔKd的比例因子分别为K1＝0.006／3＝0.002、K2＝K3＝0.009／3＝0.003。

3.3 隶属度函数的确定

确定上述5个模糊语言变量的模糊集后，各模糊语言值还须由隶属度函数来描述。常用的隶属度函数有高斯型函数、梯形函数、三角形函数，考虑到运算的简便性和系统的灵敏度，e、ec、ΔKp、ΔKi、ΔKd对应的模糊集均采用三角形函数来进行描述，隶属度函数图像如图3所示。

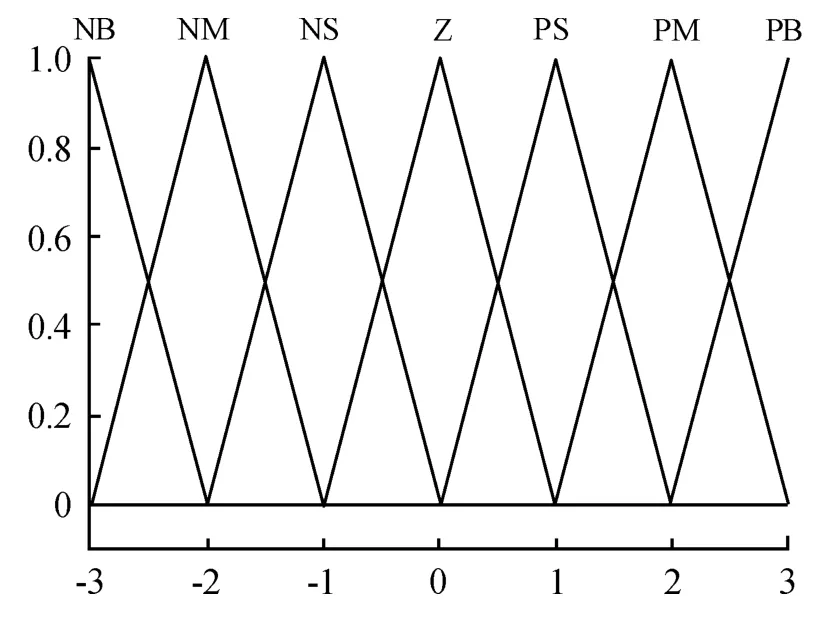
图3 e、ec、ΔK p、ΔK i、ΔK d的隶属度函数

3.4 模糊控制规则

模糊控制的核心是模糊控制规则，制定模糊控制规则的目的是为了让系统获得更好的控制性能。因此，模糊自适应PID控制器在控制pH值时，对Kp、Ki、Kd的自适应调整应满足以下一般原则。

1）当偏差e较大时，为减少系统响应时间，提升响应速率，Kp应取较大值；为避免e瞬时变化大，引起微分过饱和现象，Kd应取较小值；Ki可以取0，以防止系统出现过大的超调。

2）当偏差e和偏差变化率ec的值为中等大小时，为控制pH值时具有较小的超调量，应取较小的Kp；Ki、Kd可以取值适中，在一定程度上可让系统保持较理想的响应速度。

3）当偏差e较小时，为尽量避免系统出现振荡现象，使系统的稳态特性良好，可适当增大Kp、减小Ki；考虑到系统的抗干扰能力，Kd可依据ec值来选取，一般来说，当ec值较小时，Kd可适当取大，当ec值较大时，Kd可适当取小［13］。

根据以上规则和实际生产操作经验，对ΔKp、ΔKi、ΔKd设定的控制规则如表2所示。

表2 ΔK p／ΔK i／ΔK d模糊控制规则

模糊控制规则表建立后，对输入的e和ec，系统在规则表中找到对应的模糊决策，经Mamdani模糊推理算法［14］，计算出ΔKp、ΔKi、ΔKd的模糊量，然后运用面积重心法来对ΔKp、ΔKi、ΔKd进行反模糊化计算［15］，得出其精确值，使用式（10）—式（12）得出整定后的Kp、Ki、Kd，最后由PID控制器完成输出，其工作流程如图4所示。

图4 系统工作流程

3.5 PID参数整定

使用PID控制器进行控制前需要确定3个参数Kp、Ki、Kd的初始值，初始参数的整定方法使用的是Ziegler-Nichols参数整定法［16］，该方法求得的参数不完全准确，只能作为参考，具体结果还需要结合实际应用情况进行调整。控制器参数的推导可参照Ziegler-Nichols参数整定表进行，如表3所示。

表3 Ziegler-Nichols参数整定

积分时间常数Ti＝Kp／Ki，微分时间常数Td＝Kd／Kp。已知系统的传递函数为式（9），可知R＝2.2、T＝80、τ＝30，结合表3、式（9）求得Kp＝1.45、Ki＝0.024、Kd＝21.75。结合实际生产，对参数进行调整，具体的调整方法为：参考Ziegler-Nichols法整定的结果，对pH值控制系统尝试不同的参数，直到Kp、Ki、Kd的选取可使常规PID控制器的控制效果达到相对理想的状态，最终的参数调整为：Kp＝1.5、Ki＝0.03、Kd＝22.5。

4 仿真分析与实验结果

4.1 仿真分析

为验证上述理论，在Matlab／Simulink仿真环境下搭建了常规PID控制和模糊自适应PID控制2种系统的仿真模型，如图5所示。Matlab／Simulink中自带PID控制模块，可以直接调用，对“模糊＋PID”的控制结构进行整体封装，用Fuzzy-PID模块表示，图6为Fuzzy-PID模块的内部结构图。

图5 常规PID控制和模糊自适应PID控制仿真模型

图6 Fuzzy-PID模块内部结构

系统的仿真时间设定为500 s，pH值设定为4.5。常规PID控制器和模糊自适应PID控制器初始参数如文中3.5节所述，均设定为：Kp＝1.5、Ki＝0.03、Kd＝22.5。2种控制器的控制效果仿真结果如图7所示。

图7 仿真结果曲线

由图7可以看出，常规PID控制器和模糊自适应PID控制器最后都能消除静态误差，实现pH值稳定，稳态值分别为4.51、4.49，均与设定值4.5接近。常规PID控制器输出曲线的峰值为5.68，超调量为26.22%，达到稳定状态的时间为283.28 s；模糊自适应PID控制器输出曲线的峰值为5.00，超调量为11.11%，达到稳定状态的时间为17.10 s。模糊自适应PID控制器相比于常规PID控制器超调量少57.63%、调节时间为常规PID控制器的6.04%。

在实际工业生产中，pH值控制往往存在众多干扰因素，干扰主要来源有流量、浓度的变化等，为模仿实际生产中的干扰，在300 s处给系统添加干扰，干扰源为输出值为1的阶跃信号，得到图8的仿真效果。

图8 带干扰的仿真曲线

由图8可以看出，常规PID控制器和模糊自适应PID控制器在面对同样大小的干扰时，pH值波动的幅值相差不大。常规PID控制器使pH值恢复至稳定状态所需的时间为164.61 s，而模糊自适应PID控制器可凭借在线调整PID参数的优势来应对干扰的发生，可快速克服干扰的影响，使pH值恢复至稳定状态所需的时间只要18.23 s，恢复时间为常规PID控制器的11.07%，相较于常规PID控制器有更好的抗干扰能力。

4.2 实验结果

实验用的主控设备为西门子S7-200PLC和工控机，工控机和PLC通过控制变频器调节电动机转速，电动机带动加药计量泵输出合适的药剂量，实现对pH值的控制，pH值实际输出值通过pH计反馈到PLC。

在实验系统中，由PLC来实现PID控制器的功能，模糊推理算法则利用用于过程控制的OPC技术建立Matlab与工控组态软件的实时通讯来实现。Matlab负责完成模糊推理算法的计算，工况组态软件将计算结果通过OPC通讯采集显示，并传输给PLC完成执行机构的控制。

实验中pH值设定为4.5，常规PID控制器和模糊自适应PID控制器初始参数如文中3.5节所述，上位机组态软件分别显示常规PID控制器、模糊自适应PID控制器实验时pH值的实时变化曲线，2种控制器控制效果的实验结果如图9、图10所示。

图9 实验结果

图10 带干扰的实验结果

由图9可以看出，在55分42秒处出现峰值，常规PID控制器输出曲线的pH峰值为5.78，超调量为28.44%，较难达到稳定状态；模糊自适应PID控制器输出曲线的pH峰值为5.18，超调量为15.11%，约3 s后就达到较稳定状态。

由图10可以看出，在3时3分57秒处给系统添加干扰，常规PID控制器pH值从4.5减小到3后再回调到4.5附近振荡调整，较难达到稳定的4.5；模糊自适应PID控制器pH值从4.5减小到3.5后再回调到4.5，约4 s后就达到稳定状态。

5 结论

1）仿真时常规PID 控制器的超调量为26.22%，模糊自适应PID 控制器的超调量为11.11%，比常规PID控制器的超调量少57.63%；实验时常规PID控制器的超调量为28.44%，模糊自适应PID控制器的超调量为15.11%，比常规PID控制器的超调量少46.87%。

2）仿真时常规PID控制器从开始到使pH值达到稳定状态所用的调节时间为283.28 s，而模糊自适应PID控制器所用的调节时间为17.10 s，调节时间为常规PID控制器的6.04%；实验时常规PID控制器较难达到稳定状态，而模糊自适应PID控制器约3 s后就达到较稳定状态。

3）仿真时面对干扰时，常规PID控制器使pH值恢复至稳定状态的时间为164.61 s，而模糊自适应PID控制器只需要18.23 s，为常规PID控制器的11.07%；实验时常规PID控制器pH值从受干扰回调到设定值附近振荡调整，较难达到稳定的设定值；模糊自适应PID控制器pH值回调后约4 s后就达到稳定状态。