面向表面质量的镍基高温合金铣削参数多目标优化研究

田应权，尹瑞雪，易望远，欧 丽

（贵州大学机械工程学院，贵阳 550025）

0 引言

高温合金加工制造技术研究一直以来是我国制造业发展的重点，铣削作为金属加工的常用方式之一，常用于加工高温合金的材料表面。高温合金可大量用于航空航天领域高机械性能零部件的制造［1］。据报道，飞机发动机质量的一半以上来源于高温合金材料［2］。针对高温合金在切削加工过程中出现的表面质量问题，通过调整铣削加工参数来提高高温合金的切削加工质量已成为拓宽该材料应用领域的关键因素。镍基高温合金因具有切削生热高、刀具磨损快、材料硬度高等特点被认定为一种典型的难加工材料。因此，如何借助机器学习技术获取相对最优工艺参数，以此提升镍基高温合金的加工质量具有重要意义。

目前，国内外学者对表面质量的工艺参数优化问题开展了许多研究。史丽晨等［3］将车削后GH2132线材的表面粗糙度、尺寸误差和表面显微硬度作为优化目标，建立了该材料表面灰色关联度多目标预测、优化模型，并确定了可行工艺参数域。Milan等［4］建立了车削聚甲醛共聚物（POM-C）连续型材零件的总加工时间估算模型，以已加工表面质量（表面粗糙度和工件挠度）和工件材料可加工性（有利的芯片形式）为3个实际约束，优化了单个零件加工的总时间。郭彦军等［5］为提高硫化锌（ZnS）晶体表面质量，采用正交实验法，将表面粗糙度和表面形貌特征作为表征表面质量优劣的指标，得到了车削高质量表面ZnS晶体最佳加工参数。王熔等［6］以加工时间和变形量最小作为优化目标，采用二级逐步回归数学方法建立切削残余应力预测模型，并运用粒子群算法优化薄壁弧形零件切削参数。韩辉辉等［7］提出一种多目标QPSO-Elman网络下的参数优化，在仿真实验中发现该方法降低了加工成本，提高了切削速率，优化了表面粗糙度。Sheng等［8］提出一种考虑加工能耗与效率的切削参数优化方法，通过实验拟合和正交实验，建立了以能耗最小和加工时间最快为目标的多目标优化模型。赵飞等［9］利用金豺狼优化算法（GJO），以切削速度和进给量为待优化切削参数，将施加功率、切削力、进给量、粗糙度等设置为约束，建立了最大化生产率和最低成本的多目标优化模型。赵义豪等［10］提出用黑洞-连续蚁群优化算法ACOR对车削参数进行多目标优化，以最低切削比能和最小表面粗糙度为优化目标，为车削能效和加工质量的提高提供了新方法。王慧等［11］通过响应面法建立了高速铣削航空铸造钛合金Ti-6Al-4V表面粗糙度预测模型，并采用遗传算法对铣削参数进行多目标优化。Usgaonkar等［12］使用CNSL作为切削液设计了磨削实验，提出表面粗糙度预测模型，并通过参数优化获得最小表面粗糙度的最佳切削参数。Osorio-Pinzon等［13］确定最小化切削力、最大化微观组织细化以及最大限度地提高材料去除率3个目标，提出了一种多目标粒子群优化（PSO）算法，在低切削力、高组织细化和高材料去除率之间得出权衡点。郭斌等［14］以表面粗糙度为约束条件，以最大材料去除率为目标对6061铝立铣加工，并用遗传算法对主轴转速、进给速度和切深三个铣削参数进行多目标优化。孙杨等［15］首先用响应曲面法建立DD98表面粗糙度预测模型，然后用BP神经网络进一步对响应曲面法得到的预测模型进行优化得到优化模型。李韩博等［16］建立了目标为SPIF纵向和横向表面粗糙度整体最优的响应模型，并由此建立成形参数多目标优化模型。冯美强等［17］利用信赖域方法与最小响应面加点准则（MSP），优化了工艺参数，提高了翼子板成形质量。高筱彤［18］基于遗传算法，采用优化原理，构建了以表面粗糙度和残余应力为优化目标的多目标优化数学模型。

综上所述，在目前的研究中，对于铣削表面粗糙度预测及切削参数优化大多都只是将其分为两部分来研究，或仅利用多元线性回归分析，没有将其综合起来考虑。而利用改进神经网络在预测表面粗糙度的同时对材料去除率进行评估的研究相对薄弱。因此，本文针对数控铣削镍基高温合金表面粗糙度及材料去除率的工艺参数优化问题，考虑工艺参数对表面粗糙度不存在线性映射关系，使用SSA-BP神经网络以不同组合的工艺参数作为输入，以表面粗糙度作为输出建立预测模型。基于NSGA-Ⅱ算法建立以最优表面粗糙度、最大材料去除率为目标的主体优化模型，得到Pareto最优解集。对Pareto最优解集进行TOPSIS最优解决策，得到综合优化表面粗糙度和材料去除率的加工参数组合，为数控铣削加工的高质量、低成本优化提供新方法。最后，对实验中切削参数影响表面粗糙度的情况进行分析，为实际加工中的工艺参数选取提供理论指导。

1 铣削实验方案及数据采集

1.1 实验基础

数控铣削实验材料选用难加工金属材料镍基高温合金Inconel 718。该材料强度高，具有良好的耐温性和耐腐蚀性，被广泛应用于汽车和航空航天行业［19］。实验在南通VM600加工中心进行，选用带NACO纳米复合涂层的硬质合金钨钢铣刀进行平面铣削加工。刀具采用螺旋角45°的四刃立铣刀，其刃径和柄径均为10 mm，刃长为25 mm，总长为75 mm，刀具材料参数如表1所示。在此基础上，搭建如图1所示的铣削表面粗糙度测量系统。

图1 铣削表面粗糙度测量系统实物

表1 刀具材料参数

铣削加工后采用三维白光干涉仪（GTK-19-1030）进行测量表面粗糙度。三维白光干涉仪是一种利用干涉原理测量物体表面样貌的仪器，由照明光源、光学成像、垂直扫描以及数据处理系统组成，通过白光干涉条纹亮度解析被测样品的形貌和相对高度。为减小实验中测量表面粗糙度时存在的偶然误差，对任一次实验参数加工材料表面随机取3个不同位置点进行测量，计算3次Ra的平均值，将其作为该切削参数下的实验结果。

1.2 实验设计

实验选取切削加工三要素（铣削速度v、每齿进给量fz、铣削深度ap）为铣削Inconel 718材料表面粗糙度的影响指标，设计了包括三因子四水平的64组全因子实验。结合工厂加工经验，实验因素用量取值如表2所示，切削宽度设置为铣刀直径的50%～80%，铣削宽度ae值取5 mm，由此得到实验方案。

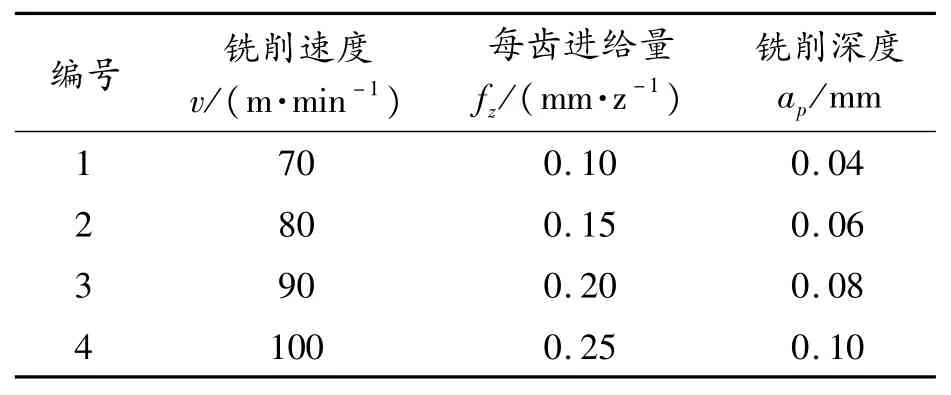
表2 实验因素水平

1.3 材料去除率计算

材料去除率是主轴转速、铣刀齿数、铣刀半径、铣削深度、铣削宽度、每齿进给量的函数，由铣削参数确定［20］。材料去除率（MRR）为单位时间内切除的金属体积，也可以由单位时间铣刀（或工件）沿进给方向前进的距离来近似定义，单位时间前进的距离如式（1）所示。

式中：Lp为单位时间前进的距离；Z为铣刀齿数；N为主轴转速。

因此，材料去除率计算式为

1.4 数据结果

根据实验的设计方案，采用扫描电子显微镜（SEM，KYKY-2800B）扫描观察铣削后Inconel 718材料表面样貌。图2和图3分别为某实验参数下某个测量点的材料表面SEM和三维形貌图。

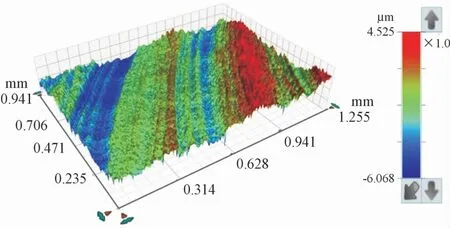
图3 Inconel718材料表面三维形貌图

通过Vision64＿5.70软件分析采集64组不同铣削参数下加工Inconel 718材料表面粗糙度数据，并由式（2）计算出不同组的材料去除率，实验结果见表3。

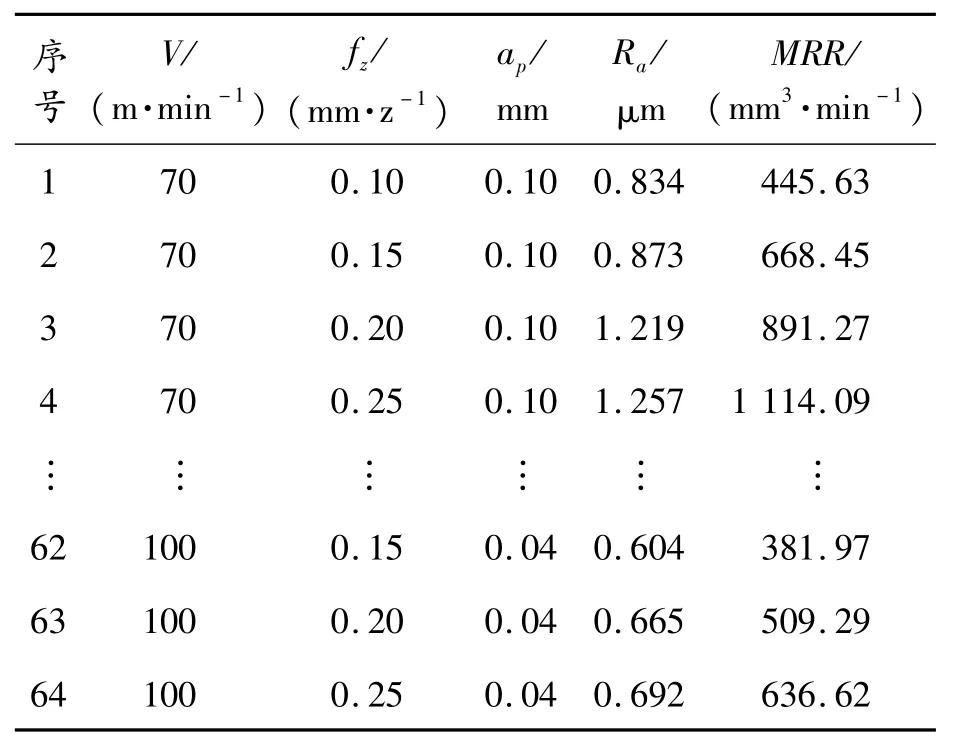
表3 数控铣削Inconel718表面粗糙度实验结果

1.5 切削参数对表面粗糙度的交互影响分析

已加工表面的粗糙度是由几何因素和物理因素共同决定的，前者与切削参数和刀具几何参数等的选取有关，后者指工件以及刀具的硬度、弹性模量等。通过实验结果可以看出，表面粗糙度随着切削速度的增大而减小，随每齿进给量的减小而减小且有局部波动情况，随轴向切深的减小而减小，但是减幅缓慢。铣削速度对表面粗糙度影响是因为当切削速度上升时，第一变形区温度迅速增大，材料发生热软化效应，硬度和切削力下降，所以表面粗糙度下降，表面质量变好。表面粗糙度随每齿进给量的减小而减小，减小进给量可以降低残留面积的高度，从而减小表面粗糙度。但当进给量减小到一定范围时，表面粗糙度下降幅度会变缓。这是由于每齿进给量取较大时，刀具和工件表面剧烈挤压，易使工件材料产生较大的变形和振动，表面粗糙度变化幅度大，而进给量较小时排泄阻力稍小，热量排出快，刀具振动幅度小。轴向切深对表面粗糙度的影响是由于当切深减小时切削力减小，导致机床振动减小，从而造成粗糙度减小，但减幅缓慢。

为了更加方便地研究切削要素对表面粗糙度特征值的交互影响关系，保持刀具结构参数保持不变。当ae不变，分别在ap＝0.1 mm、fz＝0.1 mm／z、v＝70 m／min的情况下，分析v和fz；v和ap；fz和ap对表面粗糙度特征值的交互影响如图4（a）、（b）、（c）所示。由图可知，v和fz；v和ap；fz和ap对Ra的响应曲面变化明显，说明其对Ra的交互影响显著。随着v的增大和fz的减小，Ra呈现出减小的趋势，Ra的极小值点在v为98～100 m／min和fz为0.1～0.15 mm范围处。随着v的增大和ap的减小，Ra呈现出减小的趋势，Ra的极小值点在v为100m／min和ap为0.04mm范围处。随着fz的减小和ap的减小，Ra呈现出减小的趋势，Ra的极小值点在fz为0.1 mm 和ap为0.04 mm范围处。

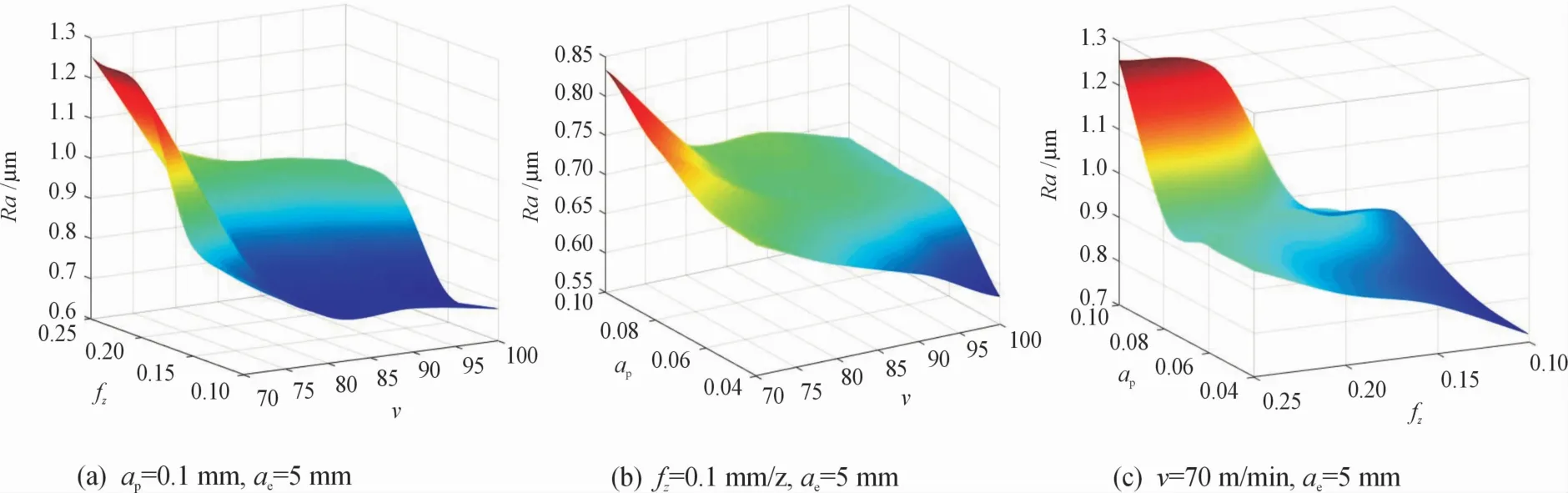
图4 切削要素对表面粗糙度特征值的交互影响曲面

2 SSA-BP表面粗糙度预测模型

2.1 BP神经网络

BP神经网络是一种常用的人工神经网络，使用反向传播算法来训练网络。该算法通过计算输出值与目标值之间的误差，并将误差逐层反向传递到网络中的每个神经元，以调整网络中每个神经元的权值和偏置，从而实现对网络的优化。反向传播算法将误差逐层反向传递，计算出每个神经元贡献的误差，并根据该误差值来更新权值和偏置，以最小化误差为目标，提高神经网络性能。最终，通过反复迭代训练，网络达到较好的收敛状态，从而实现对输入数据的分类和识别等目的。BP神经网络由输入层、隐含层和输出层构成，每一层都由一定数量的神经元构成。

采用经验公式确定隐含层节点的选取范围［21］，如式（3）所示。经多次模拟后确定神经网络参数为3-7-1，构建的神经网络结构如图5所示，输入层输入参数为数控铣削速度v、每齿进给量fz、切削深度ap，输出层输出参数为表面粗糙度Ra。

图5 神经网络结构示意图

式中：j为隐含层节点个数；m为输出层节点个数；n为输入层节点个数；a为为0～10的整数。

2.2 麻雀搜索算法

麻雀搜索算法是受麻雀的觅食行为和警惕行为的启发而提出的一种新型群体智能优化算法。该算法相对新颖，具有快速收敛和寻优能力强大的优点［22］。

将由n只麻雀组成的种群表示为X，并定义麻雀的适应度为f。在SSA中，发现者的位置更新公式如式（4）所示。在搜索过程中，具有较好适应度值的发现者会优先获取食物。

式中：t为当前迭代数；N为最大迭代次数；Xij为第i个麻雀在第j维中的位置信息；a为（0，1］的随机数；Q为服从正态分布的随机数；L为单位行向量；R2和ST分别表示预警值和安全值。

麻雀加入者的位置更新表达式为：

式中：XP为当前发现者所处最优位置；Xworst则表示适应度最低的麻雀位置；A＋表示只随机包含1与－1的行向量。

反捕食行为的种群位置更新公式为

式中：Xbest为当前的全局最优位置；β为服从正态分布的随机数；K为［－1，1］的随机数；fi为个体适应度值，fbest和fworst分别为当前全局最佳和最差的适应度值；ε为接近0的常数，以避免分母为0。

2.3 SSA-BP神经网络

传统的神经网络模型需要多次训练来不断调整权值和阈值以提高精度。但使用麻雀搜索算法可以直接确定最优权值和阈值，不需要多次随机权值和阈值训练，避免产生过度训练。此外，它还可以减少局部最优解的影响，提高预测数据的准确性。因此，采用SSA算法优化BP神经网络的权重和阈值。适应度值是选取铣削实验数据的整体均方误差。适应度函数越小，表明训练更准确，并能提高预测精度。SSA-BP回归预测算法的流程如图6所示。

图6 SSA-BP流程

2.4 表面粗糙度预测结果

根据表3中的实验采集数据分别建立传统BP和SSA-BP神经网络来进行铣削高温合金Inconel 718表面粗糙度预测，以第1—50组为训练集，第51—64组为测试集。将训练集的数据导入传统BP和SSA-BP模型中进行训练，并对其训练结果的误差进行比较。对神经网络的部分参数设置：训练次数均为2 000次；学习速率均为0.01；训练目标最小误差均为1×10－7，预测结果如图7所示。

图7 神经网络表面粗糙度预测结果

由图7可知，BP神经网络模型的预测值与真实值的偏差大于SSA-BP神经网络模型的预测值与真实值的偏差。SSA-BP神经网络模型预测能力有明显提升，该预测模型在测试时间段都有较好的预测结果。对14组测试样本进行验证，误差值如表4所示。

表4 SSA-BP和传统BP神经网络预测误差值

由表4可知，在表面粗糙度预测中，SSA-BP比BP神经网络模型预测的误差平方和SSE、平均绝对误差MAE、均方误差MSE、平均绝对百分比误差MAPE均有不同程度下降。其中，SSE下降0.04μm2，MAE下降0.023μm，MSE下降0.003 μm2，MAPE下降3.58%。根据MAE、MSE、MAPE指标，SSA-BP神经网络模型的预测精度明显提升。结果表明，利用麻雀搜索算法优化BP神经网络模型来预测铣削Inconel 718材料表面粗糙度具有更好的准确度。

此外，当评价神经网络性能的决定系数R2值越接近于1时，其网络模型在同等参数数据和相同的训练迭代次数上有着更好的准确精度与更强的稳定性能。由表4可以看出，2种神经网络模型中SSA-BP神经网络的R2值为0.985 7，而BP神经网络的R2值为0.921 7，预测目标的决定系数都接近于1，误差在允许范围内，故SSA-BP神经网络对铣削Inconel 718表面粗糙度的预测精度满足需求。但相比于BP神经网络模型，SSA-BP神经网络的R2值高出6.4%，故采用SSA-BP神经网络模型的准确精度与稳定性能更优。其中，SSA-BP神经网络模型的适应度曲线如图8所示。

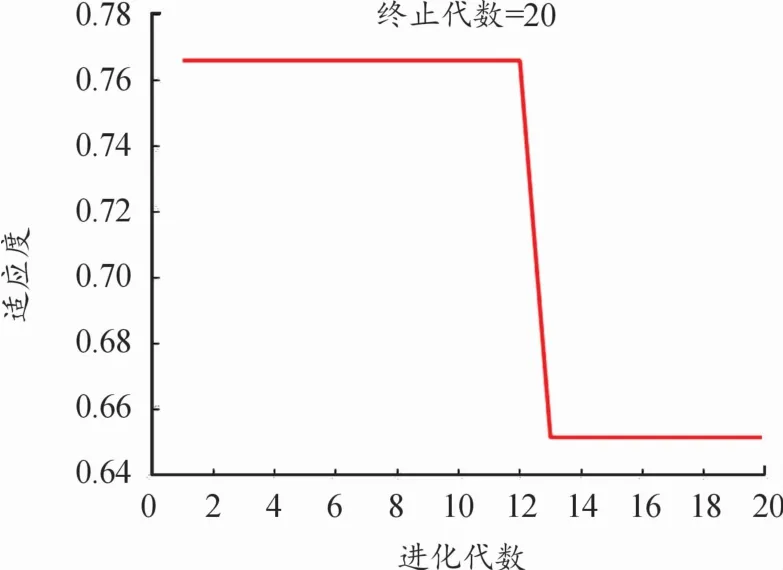
图8 SSA-BP适应度曲线

3 基于神经网络的NSGA-II算法多目标优化模型构建

3.1 工艺参数多目标优化模型的求解

NSGA-II（第二代非支配排序遗传算法）是一种对于解决多目标优化问题具有良好收敛和鲁棒性的遗传算法，是多目标优化算法的一种。作为先搜索再决策的全局优化算法，其由于运行速度快、收敛性好、通用性强、适用性广等优点被广泛应用于多目标优化问题之中，许多学者用其进行切削参数多目标优化研究并达到了预期效果。因此本文选择NSGA-Ⅱ解决所提出的数控铣削参数多目标优化问题。

根据所提出的数控铣削参数优化问题，设置优化目标为数控铣削加工的表面粗糙度及材料去除率，记为Ra和MRR。待优化参数为铣削速度v、每齿进给量fz、铣削深度ap，即SSA-BP神经网络输入参数。构建基于NSGA-Ⅱ算法的主体模型，数控铣削参数多目标优化模型如式（7）所示。

其中：f1表示SSA-BP表面粗糙度预测模型；f2为材料去除率函数；Se为每齿铣削面积；v、fz、ap为多目标优化模型的待优化变量，其输入范围如式（7）所示。

具体步骤：①针对待解决数控铣削参数优化问题，建立SSA-BP神经网络数控铣削表面粗糙度预测模型及材料去除率模型。②设置NSGA-II多目标优化主体模型参数，即种群个数、最大迭代次数、交叉概率、变异概率等。③染色体编码、初始化种群。采用实数编码的方法对染色体进行编码，即在变量范围内的随机生成一组优化变量，组成一个个体。④调用SSA-BP神经网络模型与材料去除率模型作为NSGA-II多目标优化主体模型的目标函数。⑤进入NSGA-II算法流程，直至迭代结束。⑥获取最后一代种群中的Pareto Front最优解集的工艺参数及与之对应的优化目标值，所获取的工艺参数即针对待优化问题的Pareto最优解。根据数控铣削参数多目标优化模型，设定最大迭代次数为100，种群大小为100，交叉比例为0.8，变异概率为0.05，迭代到最大迭代次数后得到的Pareto Front最优解集，如图9所示。

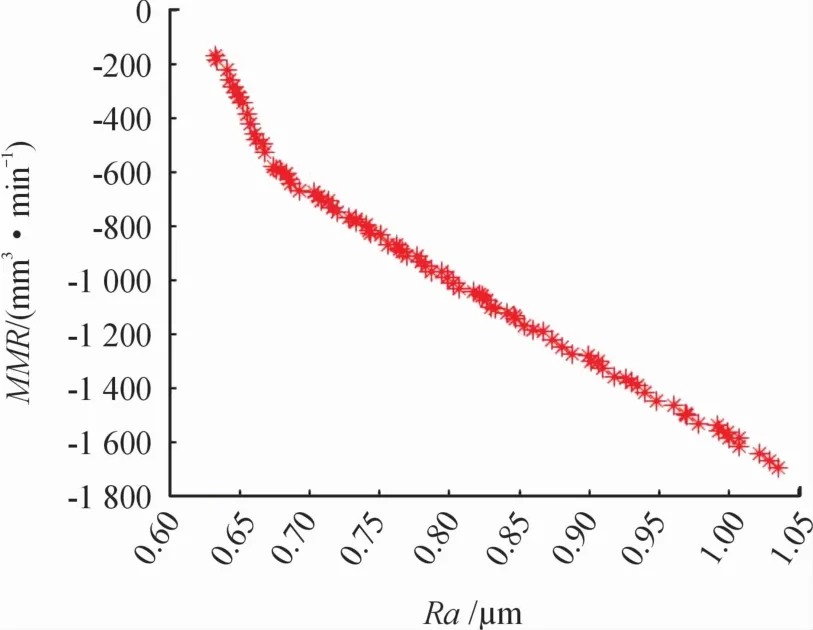
图9 多目标优化的Pareto结果

3.2 优化结果分析

通过NSGA-Ⅱ优化后得到Pareto Front最优解集，需要进行最优解的确定，因此对优化后得出的最优解集使用TOPSIS法进行最优解决策。TOPSIS法又称理想解法，是一种有效的多指标评价方法。其基本原理是通过构造监测评价对象的正理想解和负理想解，即各指标的最优解和最劣解；通过计算每个方案到理想方案的相对贴近度，即靠近正理想解和远离负理想解的程度来对方案进行排序。若评价对象与最优解的距离最近与最劣解的距离最远，则该评价对象为最优，反之最劣。

最终的Pareto Front最优解集包含多组参数，对解集中的对象进行相对优劣性的排序，通过排序决策出最优解。为了验证铣削参数的优化效果，使用TOPSIS对实验方案中的数据进行最优方案分析，决策出未进行优化时的最优方案，优化结果如表5所示。

表5 优化前后结果

优化结果表明，Inconel 718材料已加工表面粗糙度较优化前降低了12.8%，材料去除率提高了20%。由此可见，应用NSGA-II算法优化降低Inconel 718材料已加工表面粗糙度、提高材料去除率显著。

4 结论

1）以数控铣削难加工材料Inconel 718表面粗糙度Ra为预测目标，建立了SSA-BP神经网络模型，设计了数控铣削三因子四水平全因子实验，采集了在不同铣削参数条件下的表面粗糙度数据。通过SSA算法优化BP神经网络的权重和阈值，减少局部最优解的影响，提高预测数据的准确性。经过50组训练集训练神经网络，在14组测试集中发现SSA-BP神经网络模型的预测值精度高于BP神经网络模型。在多次训练中，虽铣削过程存在不确定因素，但SSA-BP神经网络的R2值均大于BP神经网络且接近1，故该表面粗糙度预测模型能够预测加工结果。

2）对已加工表面的粗糙度受切削三要素的影响情况进行交互影响分析，对实际生产选取切削参数、优化表面质量有指导意义。

3）以最大材料去除率、最小表面粗糙度为优化目标，构建NSGA-Ⅱ工艺参数多目标优化主体模型，得到数控铣削参数优化问题的Pareto front最优解集。使用TOPSIS法对Pareto front最优解集进行最优解的决策，最终得到最优解为V＝95 m／min、fz＝0.19 mm／z、ap＝0.09 mm。该优化结果在提高材料去除率的同时，降低了已加工表面粗糙度，能对实际生产提供理论指导。