基于G1-熵权-可拓理论的边坡风险评价
2024-03-18刘立萍刘海明王雅歌吕仲鸣姚美良
刘立萍,刘海明,王雅歌,吕仲鸣,姚美良
(1.昆明理工大学建筑工程学院,云南 昆明 650500;2.中国地震局工程力学研究所地震工程与工程振动重点实验室,黑龙江 哈尔滨 150080;3.云南建工基础工程有限责任公司,云南 昆明 650501;4.中交一公局集团有限公司贝尔格莱德分公司,塞尔维亚 贝尔格莱德 11000)
0 引 言
在施工过程中,由于复杂地质环境和独特地貌的原因,边坡易发生滑坡等地质灾害,因此准确识别边坡风险等级是灾害防控的关键[1]。针对边坡风险评价的问题,不少学者做了大量深入的研究,李克钢等[2]用简单关联度对层次分析法进行改进,从而确定指标权重。梁桂兰等[3]引入熵权法,建立基于熵权的可拓模型,对工程坝基体质量进行风险等级评价。王兴霞等[4]结合层次分析法给出权重,采用Choquet模糊积分建立了边坡稳定性评价模型。王述红等[5]采用方根法,得出影响边坡稳定性最重要因素是地震力。刘永等[6]利用G1法和粗糙集理论对多属度不完备边坡数据系统进行计算和分析,并验证该方法的有效性和可行性,同时说明G1法具有普遍的适用性和计算简便的优势,解决了判断矩阵不一致的问题。Yang等[7]采用极值熵理论计算评价指标的常权权重,利用变权理论对常权理论进行优化,从而确定边坡的稳定等级。Qiao等[8]通过改进的熵权法,使评价指数从一个确定数值改为区间值,并根据可拓理论,全面分析评价指标的影响程度。刘秀等[9]采用熵权法赋权,构建一种新型的路堑边坡安全评价方法,最终得到综合关联度和与其对应的安全等级。杜岩等[10]采用主客观权重相结合的综合分析法进行权重分析,同时对可拓距计算公式进行改进,实现矿山边坡的安全指标与风险指标的综合评价。
由上述文献可知,大部分学者研究成果采用单一的权重评价方法进行赋权,单一赋权可能会造成评价结果存在一定的片面性,从而使得评价结果与实际现场情况不太一致。为此,本文基于G1法和熵权法的优势,采用G1法和熵权法,分别对主观与客观权重进行赋权,采用拉格朗日乘子法确定组合权重,在传统可拓学理论上,建立基于组合赋权的可拓理论边坡风险评价方法,并采用传统的Topsis理论验证模型可靠性,同时与GEO5数值模拟结果进行对比,以期为边坡风险评价提供参考。
1 组合赋权-可拓模型理论
基于评价指标和边坡风险等级,建立基于组合赋权的物元可拓理论模型,根据该模型,计算出可拓关联度,进而实现边坡风险等级评价。基于组合赋权的物元可拓理论模型实现过程见图1。
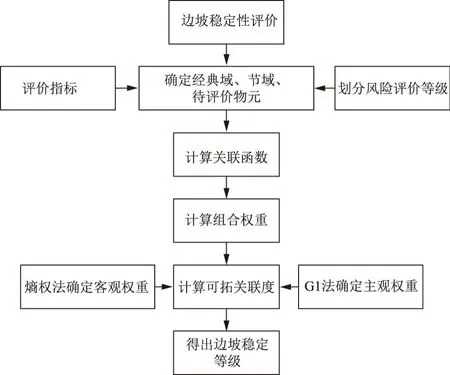
图1 基于组合赋权的物元可拓理论模型
1.1 物元
建立影响边坡稳定性的评价指标体系,并对数据进行处理。设N为边坡评价指标的稳定性等级,ci(i=1,2,…,n)为边坡稳定性等级下的第i个指标,vji为等级j下的第i个评价指标的量值范围,R1到Rn为边坡实际的工程值[11],则
(1)
1.2 经典域、节域、待评价物元
(1)确定经典域Rj。根据边坡风险等级评价标准,设评价等级分为m级,即共有m个经典域,Nj为边坡物元系统中第j个类别,vji=(aji,bji),则
(2)
(2)确定节域Rp。设Np为边坡稳定性的全部等级,vpi为指标ci关于全部等级的量值范围,vpi=(api,bpi),则
(3)
(3)待评价物元Rx。设Nx为第x个待评价的边坡,vxi为第x个待评价边坡对应的第i个评价指标取值,则
(4)
1.3 关联函数
根据经典域Rj、节域Rp和待评价物元Rx,采用下式计算关联函数,即
(5)
(6)
式中,Kji(vxi)为第x个待评价边坡第i个评价指标关于等级j的关联函数;ρ(vxi,vji)和ρ(vxi,vpi)为可拓距,可拓距分别表示实际取值vxi与区间(aji,bji)、区间(api,bpi)的距离[10],其中vji=(aji,bji)、vpi=(api,bpi)。
1.4 组合权重
1.4.1 G1法确定评价指标的主观权重w′i
G1法由我国学者提出,G1法较传统的层次分析法计算更加简便,无需构造判断矩阵。G1法是对评价指标按照重要程度进行序关系排列的一种方法,当对相邻的2个指标进行重要性赋值后,其他评价指标的相对重要程度也唯一确定,即权重唯一确定,在评价指标数量较多时,不会出现逆序的问题,无需进行一次性检验,解决了判断矩阵不一致的问题,大大简化了模型的计算。其基本的计算步骤如下:
(1)确定评价指标的序关系。Step1:若相对于某评价目标而言,评价指标ca比cb重要或者相等重要,则记为ca≥cb。Step2:若评价指标c1,c2,…,cn相对于评价目标的影响关系具有下式的关系,则称评价指标按下式确立了序关系[12],即
(7)
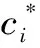
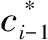

(8)
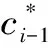
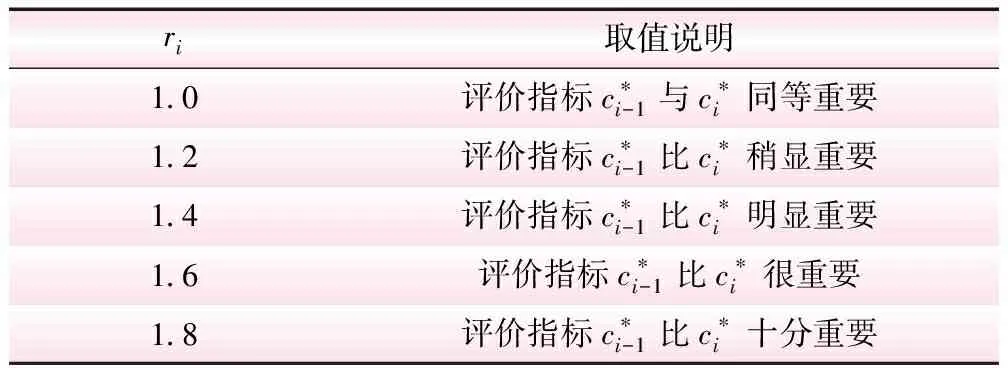
表1 ri赋值
(3)初始权重系数wi的计算。公式为
(9)
wi-1=riwi(i=n,n-1,…,2)
(10)
(4)因计算出来的权重系数wi为序关系的大小顺序所对应的权重,因此应根据原始评价指标c1,c2,…,cn的对应顺序进行权重排序,调整后的权重系数记为w′i。
1.4.2 熵权法确定评价指标的客观权重w″i
(1)初始矩阵为待评价的m个等级,n个评价指标的某个边坡,构造初始判断矩阵K,该初始判断矩阵元素kji是式(5)计算的关联函数数值,即
(11)
(2)将初始判断矩阵K归一化处理,得到新的矩阵A,即
(12)
(13)
式中,min(ki)为kji所在列的最小值;max(ki)为kji所在列的最大值。
(3)计算各评价指标的熵值Hi,即
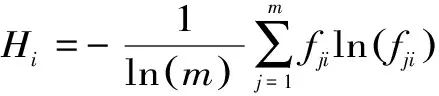
(14)
(15)
式中,fji为第i个指标下第j个等级的特征比重。
(4)计算n个评价指标的客观权重w″i,即
(16)
(17)
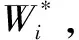
(18)
1.5 确定可拓关联度
可拓关联度Kj(Nx)为组合权重与关联函数的乘积之和,采用下式计算[5]
(19)
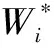
2 工程应用
选取西双版纳傣族自治州的波罕、丹兰和章芭地块的边坡为研究对象,工程区所在的景洪市抗震设防烈度为Ⅷ度。场地属于景洪盆地西部,属山地缓坡地貌单元,原始坡度介于20°~30°之间,局部坡度较陡,坡度达40°,拟建场地气候属北热带和南亚热带湿润季风气候,兼有大陆性气候和海洋性气候,年平均降雨量1 197.6 mm,降雨量主要集中在6月~9月,占全年总量的85%,雨季期间大气降水会顺坡及顺沟汇集,场地及附近无对场地有影响的地表水体、地表径流分布。
勘察范围内共分为1~4号边坡,在每个边坡中分别选取其中代表性的1个边坡。边坡范围及编号见图2。根据现场的勘察报告,边坡稳定性评价指标见表2。
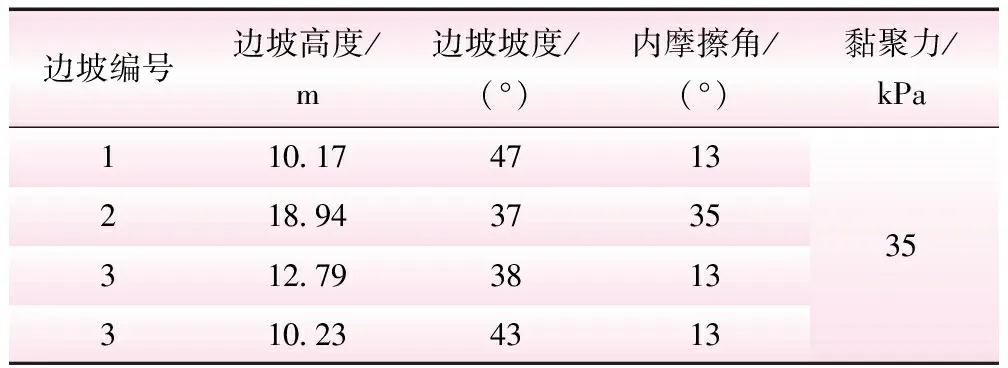
表2 边坡稳定性评价指标
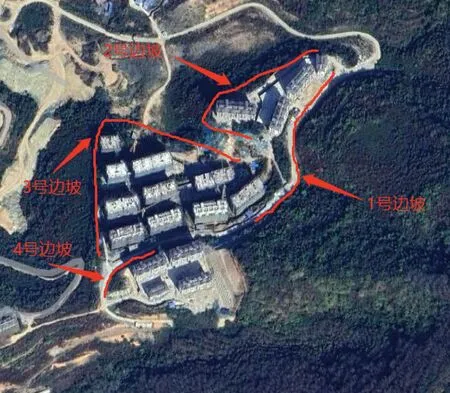
图2 边坡范围及编号
在利用组合赋权-物元可拓模型进行分析的过程中,由于评价指标的选取直接影响着评价结果,因此本研究从内部因素和外部因素的角度出发,选取边坡高度、边坡坡度、抗震烈度、年均降雨量、内摩擦角和黏聚力6个参数作为评价指标[14-16],分别记为c1、c2、c3、c4、c5和c6。
根据边坡的现场勘察资料,通过参考相关学者的研究成果[17-19]和现行规范,并结合现场的工程师的意见,将边坡的稳定性划分为5个等级,分别用Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ表示,分别代表边坡的稳定性为非常稳定、稳定、基本稳定、不稳定和极不稳定。各评价指标风险等级取值区间见表3。

表3 各评价指标风险等级取值区间
2.1 构建物元可拓模型
由于计算每个边坡的步骤大致相同,仅以1号边坡为例进行计算。
(1)经典域Rj。根据表3可知,风险等级共5个,因此有5个经典域,以等级Ⅰ为例,经典域为
(2)节域Rp。建立节域Rp,即
(3)待评物元模型Rx。根据表2参数确定边坡的待评物元模型,即
2.2 确定关联函数
根据式(5)和式(6)计算1号边坡各个指标对应各风险等级的关联函数,计算的结果见表4。

表4 1号边坡各个指标对应各风险等级的关联函数
2.3 确定权重
采用G1法确定主观权重,熵权法确定客观权重,以拉格朗日最优乘子法确定组合权重的理论分析为基础,利用式(7)~(10)计算1号边坡的主观权重,利用式(11)~(16)计算1号边坡的客观权重,并最终利用式(18)计算出组合权重。主客观权重与组合权重见表5。
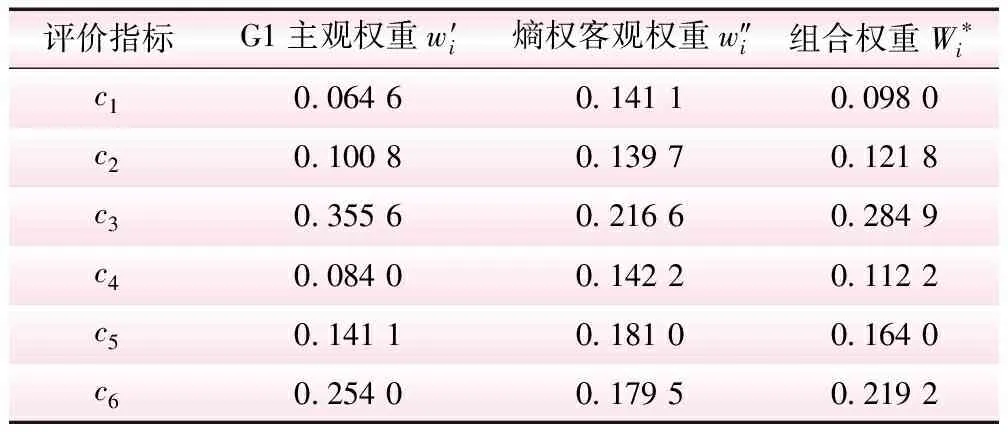
表5 各评价指标的主客观权重与组合权重
将3种方式得出的权重进行比较,结果见图3。从图3可知,组合权重处于G1主观权重和熵权客观权重之间。组合权重即考虑了主观性,又考虑了真实数据和等级标准之间的关联性,体现了数据本身的特有属性,从而使得组合权重的结果更加合理。
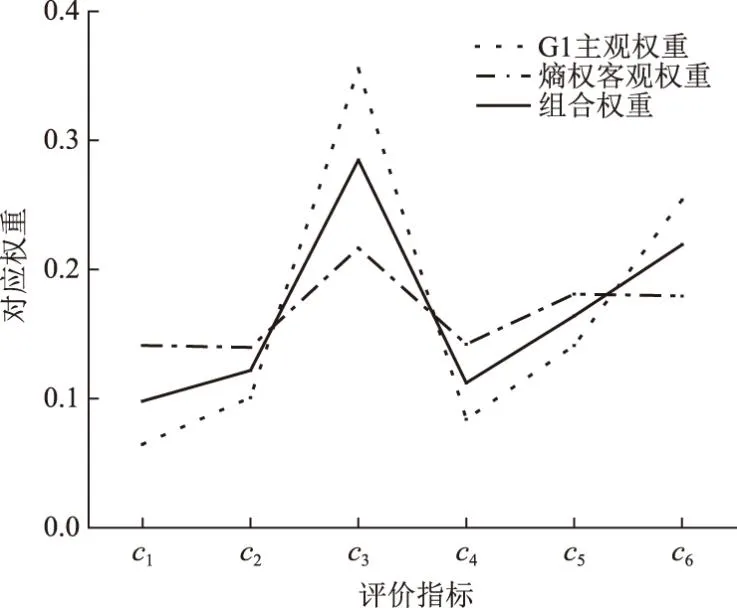
图3 权重计算结果对比
同理可得,其他3个边坡的组合权重,结果见表6。分别对比同一个边坡不同评价指标的组合权重可知,4个边坡组合权重最大值所对应的评价指标都是地震烈度c3,故地震力是影响边坡稳定性最重要的因素。

表6 边坡的组合权重
2.4 确定可拓关联度
根据式(19)计算1号边坡基于组合权重的可拓关联度。同理可得,其他3个边坡的可拓关联度,结果见表7。若Kj0=max{K1(Nx),K2(Nx),K3(Nx),K4(Nx),K5(Nx)},则称待评价的边坡等级为j0(j0=Ⅰ,Ⅱ,Ⅲ,Ⅳ,Ⅴ),Kj0为不同风险等级可拓关联度的最大值。从表7可知,对比不同风险等级的可拓关联度数值,找出最大值Kj0对应的风险等级,即可得到边坡的风险等级j0。以1号边坡为例,在可拓关联度{-0.392 7、-0.361 4、-0.111 9、-0.170 2、-0.144 5}中,可拓关联度-0.111 9最大,对应风险等级为Ⅲ级,故1号边坡稳定性等级为Ⅲ级。同理可得,2号边坡为Ⅱ级,3号边坡为Ⅲ级,4号边坡为Ⅲ级。
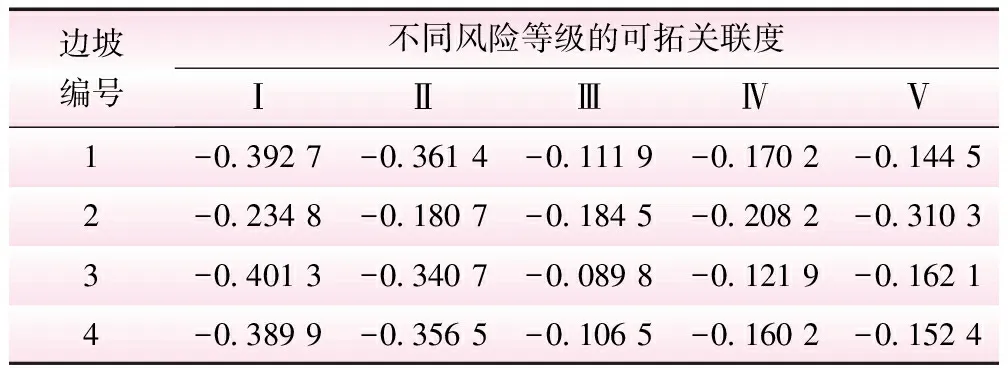
表7 边坡的可拓关联度
与其他风险评估方法对比结果见表8。从表8可知,对于2号边坡,本文得出的评价结果和Topsis方法评价结果均为Ⅱ级(稳定),而GEO5数值模拟得出的结果为基本稳定。结合表3和表8可知,6项评价指标中有2项处于极低的风险等级(Ⅰ级)且权重占比较高,所以导致了预测结果比模拟值更安全。除2号边坡的风险等级为Ⅱ级外,其余边坡的风险等级均为Ⅲ级(基本稳定),评价结果与Topsis方法的评价结果一致,同时与GEO5的数值模拟结果基本相似,与现场结果相吻合。因此,本文所构建的组合赋权物元可拓理论具有一定的实际应用价值。
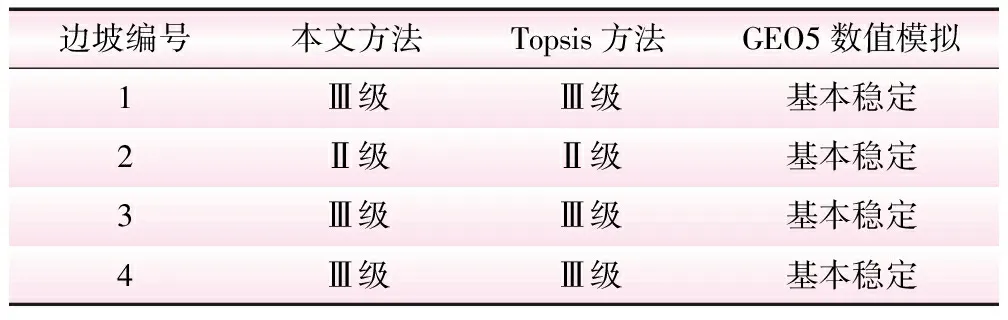
表8 多种评价结果对比
3 结 语
本文采用G1-熵权法,建立基于组合赋权的物元可拓理论模型,选取边坡高度、边坡坡度、抗震烈度、年均降雨量、内摩擦角和黏聚力6个参数作为评价指标,将边坡的稳定性划分为Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ等5个等级,分别代表边坡的稳定性为非常稳定、稳定、基本稳定、不稳定和极不稳定,对西双版纳傣族自治州的波罕、丹兰和章芭地块的边坡进行风险评价,得出以下结论:
(1)采用G1法和熵权法对主客观权重赋值,实现了主客观权重的相互结合。与单一权重相比,组合权重既考虑了主观性,又考虑了真实数据和等级标准之间的关联性,克服了单一权重的片面性,体现了工程数据本身的特有属性,更加符合工程实际。
(2)通过分析影响边坡稳定性评价指标的组合权重得出,地震力是影响边坡稳定性最重要的因素。除2号边坡的风险等级为Ⅱ级外,其余边坡的风险等级均为Ⅲ级,与Topsis方法的评价结果一致,同时与GEO5的数值模拟结果基本相似,表明采用组合权重的方法是可行的,可为类似工程提供参考。
