基于WPT-ISO-RELM模型的月径流时间序列预测研究
2024-03-18王应武白栩嘉崔东文
王应武,白栩嘉,崔东文
(1.云南省水利水电勘测设计研究院,云南 昆明 650021;2.云南省文山州水务局,云南 文山 663000)
1 研究背景
准确的月径流量时间序列预测为防涝减灾、水资源的合理配置和调度提供科学依据和指导性建议。月径流受降水、气候、人类活动等因素影响,时序数据表现出高噪声、非线性、非平稳性和多尺度等特征,导致未经数据分解处理的模型难以获得满意的预测效果[1-4]。由于月径流影响因素众多,并最终体现在随时间变化的月径流监测数据中,因此,可采用时间预测模型挖掘月径流数据的潜藏规律,进一步预测其变化趋势。近年来,时间序列预测模型已广泛应用于月径流预测,如王文川等[5]建立完全集合经验模态分解方法(CEEMDAN)、变分模态分解(VMD)和BP神经网络相融合的月径流预测模型;刘尚东等[6]将极点模态分解法(ESMD)与最近邻抽样回归模型(NNBR)结合构建耦合月径流预测模型;张璐等[7]建立VMD、相空间重构(PSR)和贝叶斯神经网络(BNN)相融合的月径流预测模型;徐冬梅等[8]基于CEEMDAN、小波分解(WD)二次组合分解技术,构建CEEMDAN-WD-粒子群优化(PSO)-最小二乘支持向量机(LSSVM)月径流组合预测模型;孙国梁等[9]构建VMD、麻雀搜索算法(SSA)与长短期记忆神经网络(LSTM)相耦合的月径流预测模型;梁晓鑫等[10]建立奇异谱分析(SSA)、梯度优化算法(GBO)与相关向量机(RVM)、支持向量机(SVM)相融合的月径流预测模型;李新华等[11]构建小波包分解(WPD)-金枪鱼优化算法(TSO)-极限学习机(ELM)组合月径流预测模型;杨琼波等[12]建立WPD、人工水母搜索算法(AJS)、数据分组处理方法(GMDH)组合月径流预测模型;席东洁等[13]建立经验模态分解(EMD)与Elman神经网络组合月径流预测模型;桑宇婷等[14]建立互补集合经验模态分解(CEEMD)与BP神经网络组合月径流预测模型;王丽丽等[15]构建SSA、灰狼优化算法(GWO)、回归支持向量机(SVR)融合月径流预测模型。
正则化极限学习机(Regularized extreme learning machine,RELM)主要为解决极限学习机(Extreme learning machine,ELM)泛化能力差、预测不稳定等问题而提出,具有训练速度快、泛化能力好等优点,已在各行业领域得到广泛应用。但在实际应用中,随机给定的输入层权值和隐含层偏差(简称“超参数”)在很大程度上影响了RELM的稳定性和预测精度。针对这一问题,PSO算法[16-17]、天牛群优化算法(BSO)[18]、蜉蝣算法(MA)[19]、鸟群算法(BSA)[20]等已被用于RELM超参数优化。
为提高月径流时间序列预测的精度,验证改进蛇群算法(Improve snake optimization,ISO)优化RELM超参数对模型性能的影响,提出小波包变换(Wavelet packet transform,WPT)-ISO-RELM预测模型,并构建WPT-SO-RELM、WPT-GWO-RELM、WPT-变色龙群算法(CSA)-RELM、WPT-鲸鱼优化算法(WOA)-RELM、WPT-樽海鞘群体算法(SSA)-RELM、WPT-侏獴优化算法(DMO)-RELM、WPT-PSO-RELM模型、WPT-ISO-LSSVM、WPT-SO-LSSVM、WPT-GWO-LSSVM、WPT-CSA-LSSVM、WPT-WOA-LSSVM、WPT-SSA-LSSVM、WPT-DMO-LSSVM、WPT-PSO-LSSVM、WPT-RELM、ISO-RELM模型作对比分析模型,通过黑河流域莺落峡水文站、讨赖河水文站1956年1月~2009年12月月径流预测实例对各模型进行验证。
2 研究方法
2.1 小波包变换(WPT)
WPT能同时对信号低频部分和高频部分进行分解,更适用于波动激烈的月径流时间序列分解。WPT对月径流原始信号进行分解,具体参考文献[11,21-22],其公式为
(1)
重构算法公式为
(2)

2.2 改进蛇群优化(ISO)算法
SO是F. A. Hashim等人于2022年提出的一种新型元启发式优化算法。该算法灵感来自于蛇的觅食和繁殖行为,即通过模拟探索阶段(觅食过程)和开发阶段(繁殖过程)进行位置更新来达到求解优化问题的目的[23]。基本SO数学描述简述如下:

Xi=Xmin+r(Xmax-Xmin)
(3)
式中,Xi为第i个个体位置;r为介于0和1之间的随机数;Xmax、Xmin分别为搜索空间上、下限值。
(2)定义温度和食物量。SO算法中,其探索、开发阶段主要受温度Temp和食物量Q的影响,温度Temp和食物量Q定义为
(4)
式中,t、T分别为当前迭代次数和最大迭代次数;c1为常数,取0.5。
(3)探索阶段。SO算法中,若食物量Q<0.25,则蛇群个体选择任何随机位置来搜索食物并更新位置。位置更新描述为
(5)
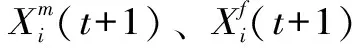
(4)开发阶段。SO开发阶段相对复杂,分为靠近猎物、战斗、交配等3种策略,3种策略均受温度Temp和食物量Q的影响。
靠近猎物策略。SO算法中,若食物量Q>0.25且温度Temp>0.6时,则蛇靠近猎物,位置更新如下
(6)
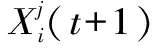
战斗或交配策略。若温度Temp≤0.6时,则蛇执行战斗或交配策略。
战斗策略位置更新为
(7)
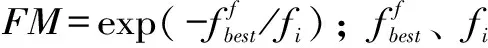
交配策略位置更新为
(8)
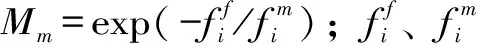
(5)种群更新。SO算法中,若有蛇蛋孵化,则随机生成位置替换最差雄性或雌性个体位置,数学描述为
(9)
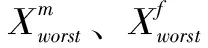
SO已被验证具有较好的寻优性能[23],但对于复杂优化问题,SO仍然存在搜索能力不足和搜索精度低等不足。为进一步提高SO的全局和局部搜索性能,本文针对常数c1、c2、c3改进如下
(10)
2.3 正则化极限学习机(RELM)
ELM是一种广义的单隐层前馈神经网络,具有较快的学习速度和良好的泛化能力。给定M个样本Xk={xk,yk},k=1,2,…,M,其中xk为输入数据,yk为真实值,激励函数为f(·),隐层节点为m个,ELM输出可表示为[24-25]
(11)
式中,oj为输出值;Wi={ωi1,ωi2,…,ωim}′为输入层节点与第i个隐含层节点的连接权值;bi为第i个输入节点和隐含层节点的偏值;λi为第i个隐含层节点与输出节点的连接权值。
在实际应用中,ELM存在过拟合、可控性弱等缺点。为克服ELM不足,Deng等[26]在ELM中引入结构风险和正则化系数C,通过参数C来调节结构风险与经验风险的比例,以改善ELM过拟合问题[27-28]。RELM数学模型目标函数表述为
(12)
受限于
(13)
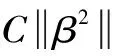
2.4 建模流程
步骤1。利用2层WPT对莺落峡水文站、讨赖河水文站月径流时序数据进行分解,得到2个高频分量[2,1]、[2,2]和2个低频分量[2,3]、[2,4],见图1。从图1可以看出,高频分量波动激烈,频率大、振幅小,大致反映了月径流时序数据的随机变化情况;低频分量波动较缓,频率小、振幅大,大致反映了月径流时序数据的变化趋势。本文选取莺落峡水文站、讨赖河水文站月径流时序数据的80%作为训练样本,剩余的20%作为预测样本。

图1 月径流时序数据2层WPT分解
步骤2。参考文献[11,21-22],利用Cao方法确定图1中低频和高频分量的输入步长a,并利用前a个月的径流分量预测未来1个月的分量值,即输入层节点数为a,输出层节点数为1。利用同样的方法确定原始月径流的输入步长a,计算结果见表1。

表1 输入步长a的计算结果
依据表1,预测模型的输入、输出可表述为
(14)
式中,M为样本数量;a为输入步长,即嵌入维度。
步骤3。利用低频和高频分量的训练样本拟合值与实际值构建均方误差(MSE),并将其作为ISO、SO、GWO、CSA、WOA、SSA、DMO、PSO算法优化RELM超参数的适应度函数,其公式为
(15)
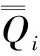
步骤4。设置ISO、SO、GWO、CSA、WOA、SSA、DMO、PSO算法的种群规模为50,最大迭代次数为200,其他参数采用算法默认值(本文着重介绍ISO算法优化过程,其他7种算法优化过程可参考ISO算法实现)。利用式(3)随机初始化蛇群个体位置Xi,将蛇群规模N分为相等的两组Nm、Nf。
RELM、LSSVM参数设置如下:RELM选用含有一个隐含层的3层网络结构,隐含层节点数设置为a(a为输入步长),激活函数选择sigmoid函数,超参数搜索空间设置为[-1,1],其中RELM网络正则化系数C设置为1×10-10;LSSVM核函数g和正则化参数γ搜索空间均设置为[0.01,2 000],式(15)为8种算法优化的适应度函数。为验证优化效果,RELM模型参数设置同上;所有模型的原始数据进行[0,1]归一化处理。
步骤5。计算蛇群所有个体适应度值,找到并保存当前最佳猎物位置Xfood。令当前迭代次数t=1。
步骤6。计算c1、c2、c3值,分别将其代入式(4)~式(8)。若食物量Q<0.25,则利用式(5)更新雄性和雌性位置;若食物量Q>0.25且温度Temp>0.6,则利用式(6)更新位置;若温度Temp≤0.6,则利用式(7)、式(8)更新位置。
步骤7。基于式(9)替换具有最差位置的雄性或雌性个体。
步骤8。利用更新后的蛇群个体位置计算适应度值,比较并保存当前最佳猎物位置Xfood。
步骤9。重复步骤6~步骤9直至满足算法终止条件。
步骤10。 输出全局最佳猎物位置Xfood,该位置即为RELM最佳超参数。利用该超参数建立WPT-ISO-RELM等模型对低频、高频分量进行预测和重构。
步骤11。利用平均绝对百分比误差MAPE、平均绝对误差MAE和纳什效率系数NSE对模型进行评价。
3 模型验证
数据来源于国家冰川冻土沙漠科学数据中心(http:∥www.ncdc.ac.cn)提供的莺落峡水文站、讨赖河水文站1956年1月~2009年12月共648组月径流时序数据,月径流过程如图1所示。从图1可以看出,莺落峡水文站、讨赖河水文站月径流序列波动性较大,复杂程度较高,呈现出较强的非线性和非平稳性,不利于直接预测。
3.1 算法实例验证
为验证ISO优化性能,基于式(15)构建8个RELM超参数寻优适应度函数fMSE,利用ISO、SO、GWO、CSA、WOA、SSA、DMO、PSO分别对各适应度函数fMSE进行20次寻优,并利用最优值fB、最劣值fW和平均值fA对8种算法的实际优化性能进行评估,见表2、3,某次寻优曲线见图2。
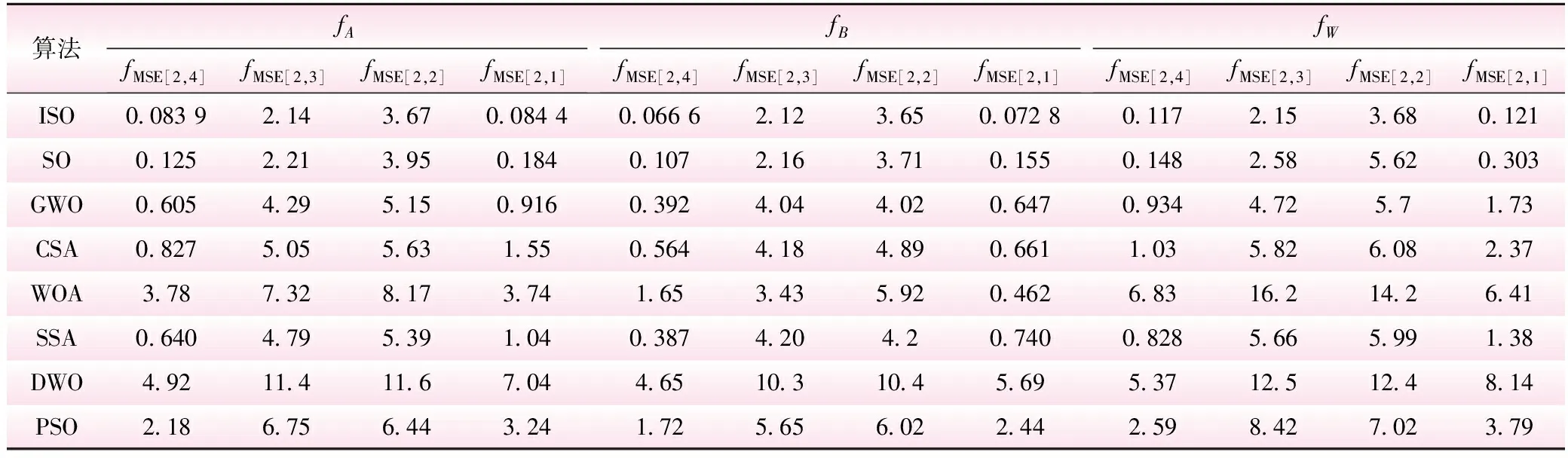
表2 莺落峡水文站月径流8种算法优化结果评估指标对比 10-3
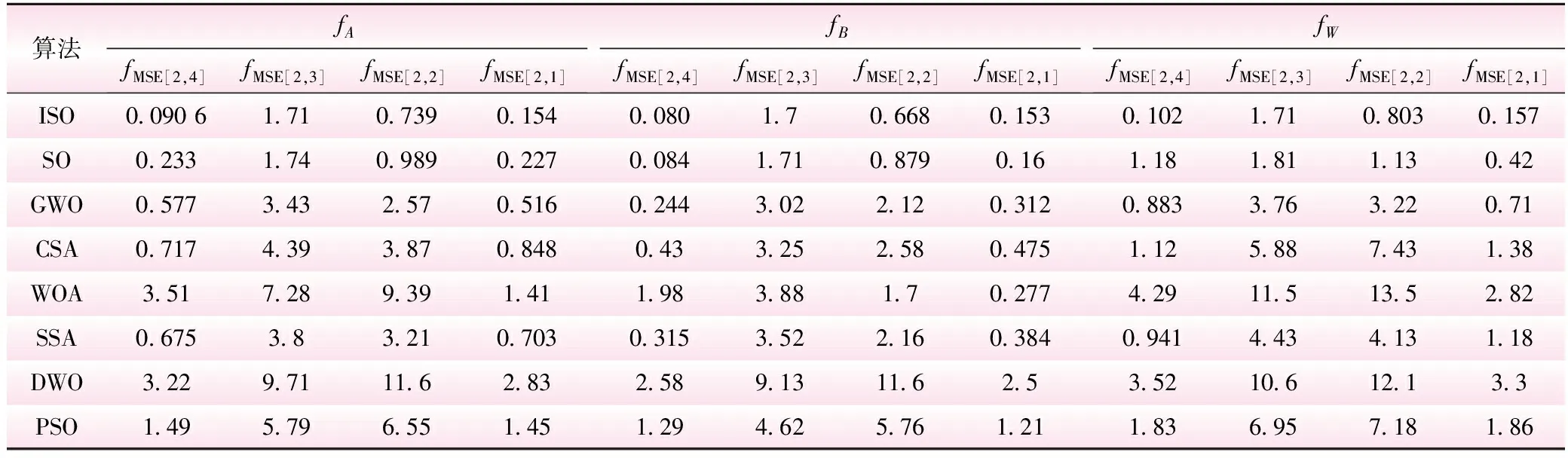
表3 讨赖河水文站月径流8种算法优化结果评估指标对比 10-3
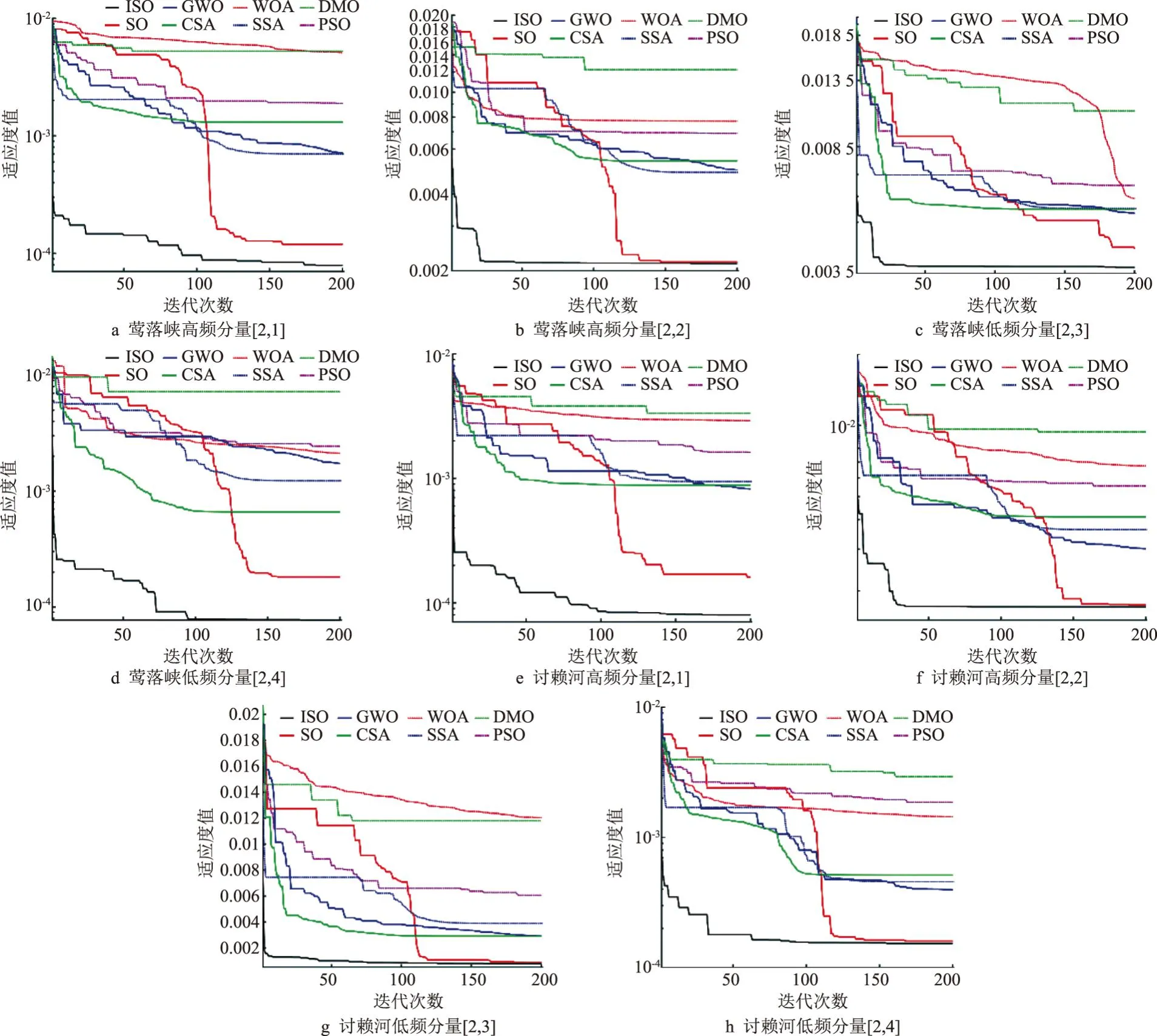
图2 ISO等8种算法实例适应度函数寻优曲线
从表2、3和图2可以得出:
(1)ISO寻优精度均优于SO、GWO、CSA、WOA、SSA、DMO、PSO等7种算法,表现出更好的寻优精度和全局优化性能,表明通过改进c1、c2、c3参数,ISO优化性能得到大幅提升。总体而言,8种算法优化性能依次是ISO>SO>GWO>SSA>PSO>DMO>CSA。
(2)从图2可以直观看出,ISO寻优精度高、收敛速度快,表现最好;PSO、DMO、CSA在实例适应度函数寻优过程中陷入局部极值,表现较差。
3.2 预测结果及分析
利用WPT-ISO-RELM等模型对莺落峡水文站、讨赖河水文站的月径流低频、高频分量进行训练及预测,将预测结果加和重构后得到最终预测结果,同时构建ISO-RELM模型对原始月径流序列进行训练及预测,见表4。
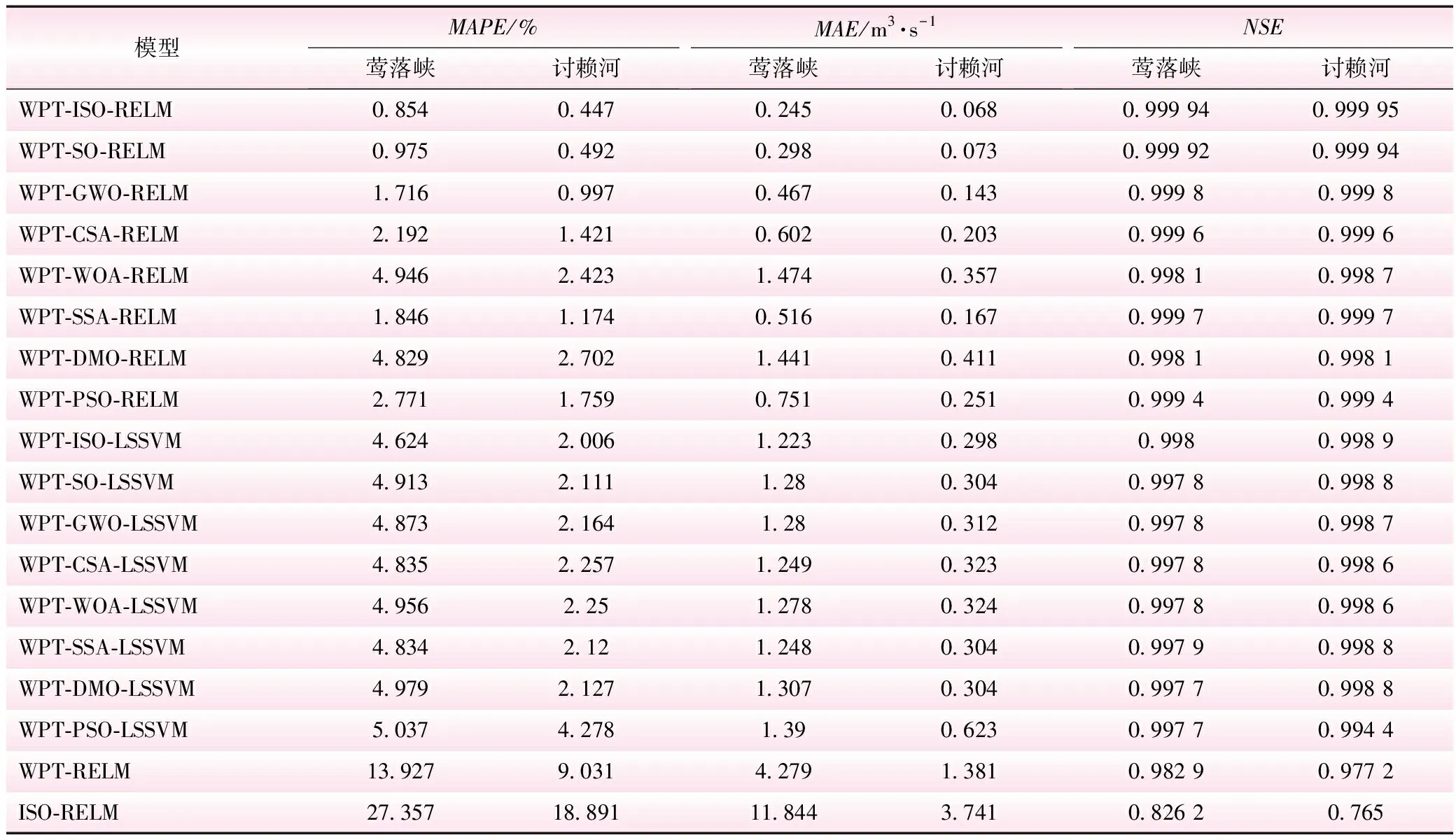
表4 莺落峡、讨赖河水文站月径流预测结果评估指标对比
由表4可知:
(1)WPT-ISO-RELM模型对莺落峡水文站月径流预测的MAPE、MAE、NSE分别为0.854%、0.245 m3/s、0.999 9,对讨赖河水文站月径流预测的MAPE、MAE、NSE分别为0.447%、0.068 m3/s、0.999 9,预测精度优于WPT-SO-RELM模型、WPT-GWO-RELM模型、WPT-CSA-RELM模型,远优于其他对比模型,具有更高的预测精度和更好的稳健性能,将其用于月径流时间序列预测是可行的。
(2)在相同预测器情形下,对于莺落峡水文站月径流序列,WPT-ISO-RELM模型预测的MAPE较WPT-SO-RELM模型、WPT-GWO-RELM模型、WPT-CSA-RELM模型、WPT-WOA-RELM模型、WPT-SSA-RELM模型、WPT-DMO-RELM模型、WPT-PSO-RELM模型分别提高12.4%、50.2%、61.0%、82.7%、53.7%、82.3%、69.2%,对讨赖河水文站月径流序列分别提高9.1%、55.2%、68.5%、81.6%、61.9%、83.5%、74.6%,表明ISO优化RELM超参数的效果要优于其他算法,算法优化性能越强,寻优精度越高,优化获得的RELM超参数越优,由此构建的模型预测精度越高。
(3)与WPT-RELM模型相比,通过优化RELM超参数构建的模型,其预测性能均得到大幅提升,表明采用智能算法优化RELM超参数,能大大改善RELM网络的预测性能。
(4)与ISO-RELM模型相比,采用WPT对月径流时序数据进行分解,其预测精度得到显著提升,表明WPT能有效将月径流原始序列分解为更具规律的低频和高频分量,大大提高了模型的预测精度。
(5)由于RELM超参数优化维度Dim=inputnum×hiddennum+hiddennum(inputnum、hiddennum分别为输入层、隐藏层神经元个数),因此,本文RELM超参数优化维度在132~756之间,属高维优化问题;而LSSVM超参数仅有2个,属2维优化问题。从表4预测结果来看,对于高维优化问题,ISO优化效果最好,SO、GWO、SSA次之,PSO、DMO、CSA优化效果较差;对于2维优化问题,虽然ISO优化效果最好,但与其他算法优化效果差别不大,其他7种算法均对LSSVM超参数有着较好的优化效果。可见,基于c1、c2、c3参数改进的ISO算法,无论是高维还是低维优化,均具有较好的全局极值寻优能力;同时也可看出,对于高维RELM超参数优化问题,算法的寻优性能对提升RELM预测精度十分关键。
4 结 论
为验证ISO改进效果和优化算法寻优能力对RELM超参数寻优效果的影响,基于WPT分解方法和ISO、SO、GWO、CSA、WOA、SSA、DMO、PSO共8种群体智能算法,提出了WPT-ISO-RELM、WPT-SO-RELM、WPT-GWO-RELM、WPT-CSA-RELM、WPT-WOA-RELM、WPT-SSA-RELM、WPT-DMO-RELM、WPT-PSO-RELM等8种组合时间序列预测模型,并构建若干对比模型,以黑河流域莺落峡水文站、讨赖河水文站月径流预测实例对各模型性能进行验证,得到以下结论:
(1)对于实例适应度函数fMSE,ISO寻优效果均优于SO、GWO、CSA、WOA、SSA、DMO、PSO,具有较好寻优精度和收敛性能,通过改进c1、c2、c3参数,能有效提升ISO极值寻优能力和平衡能力。
(2)WPT-ISO-RELM模型对莺落峡水文站、讨赖河水文站月径流的预测效果均优于其他对比模型,具有更高的预测精度和更好的稳健性能。
(3)对于高维优化问题(RELM超参数优化),ISO优化效果最好,SO、GWO、SSA次之,PSO、DMO、CSA优化效果较差;算法寻优性能对提升RELM预测精度十分关键,算法优化性能越强,寻优精度越高,由此获得的RELM超参数越优,所构建的模型预测性能越好。对于低维优化问题(LSSVM超参数优化),ISO、SO、GWO、CSA、WOA、SSA、DMO、PSO等8种算法均具有较好的优化效果,但ISO优化效果最好。
(4)WPT能有效挖掘原始序列中的内部特征信息,获得更具规律的低频和高频分量,更容易建模预测。
(5)本文提出的模型及组合方法可为相关预测研究提供参考,具有较好的实际应用和推广价值。
