基于OrcaFlex的海洋柔性管水动力分析

章仲怡

（中海油能源发展股份有限公司清洁能源分公司，天津 300450）

柔性管由于较低的弯曲刚度和较高的体积刚度可以承受较大的弯曲变形而不会影响轴向强度和压力完整性。因此，柔性管广泛用于海上石油和天然气行业[1]，作为海上平台的连接件提供了和海底设施之间的永久连接。然而，复杂的结构增加了极限强度和疲劳损伤的评估难度。

海洋环境和操作压力变化对柔性管的疲劳性能产生了负面影响。柔性管内部层的运行及相互作用非常复杂，其应力及其变化幅值的准确计算取决于柔性管的整体水动力载荷分析及危险点的确定。本文用于疲劳计算的水动力载荷谱分析涉及2个步骤：①环境载荷数据的收集和载荷情况的定义，从波浪图中选择用于全局分析的环境荷载情况；②建立OrcaFlex的水动力分析模型，对柔性管道进行全局时域分析，生成沿柔性管的轴向力和力矩的时程曲线。北部湾某平台采用的柔性管（外径168.33 mm，壁厚15.90 mm）被用于平台底部连接海管的弯曲连接处，柔性管的横截面结构如图1 所示，其中每层的形状及力学性能都有所区别。

图1 柔性管的横截面结构

1 平台海域海况分析

在柔性管的水动力分析中有规则波浪法和不规则波浪法。基于规则波浪法的柔性管载荷分析通常导致保守的结果。不规则波浪法分析更能代表现场环境，降低疲劳寿命评估中的保守度，从而产生更真实的结果，更具实际的价值。

1.1 平台所在海域的风浪流整体数据

平台位于涠洲岛西南31 km 处，水深30.3 m。根据该海域统计的8 个方向波浪载荷分布概率表，得到波浪散布分块表如表1 所示。表1 中，T为波浪周期，s；H为波高，m，表1 中的数值表示该波浪组合的统计占比。

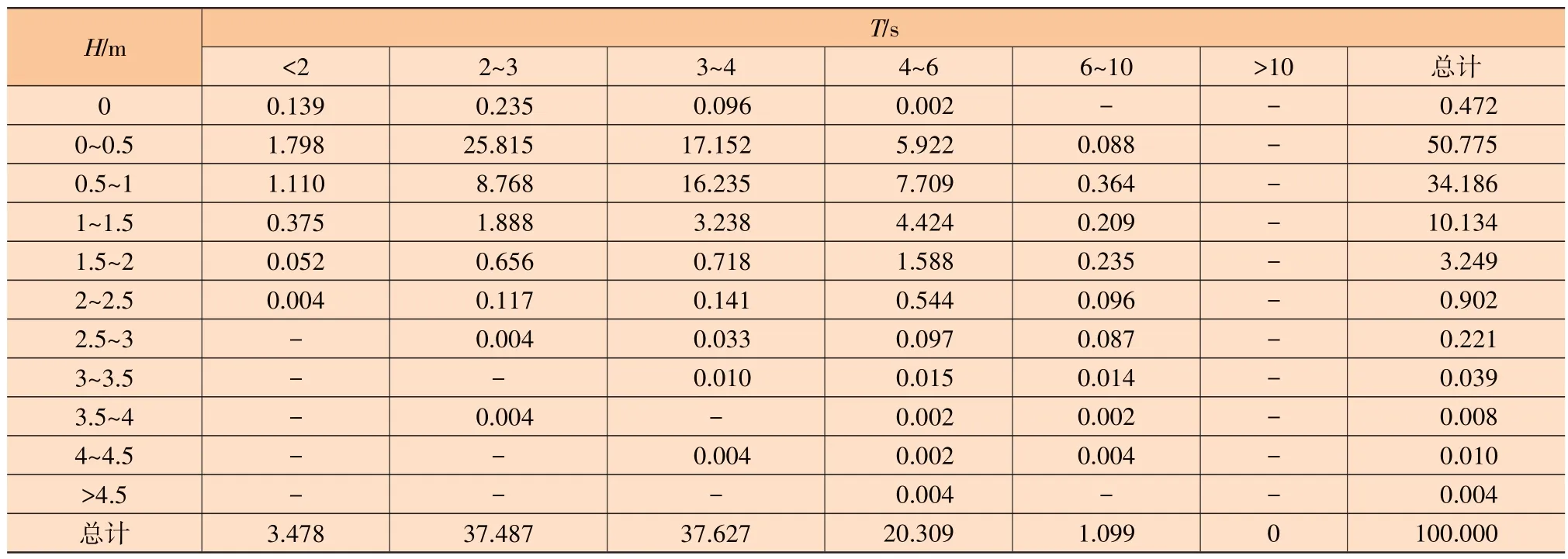
表1 波浪散布分块表 %

环境参数通常使用散点图以单独的方式描述，可以从现场测量活动中获得局部波的散点图并建立类似的波浪散布分块表。为了从波浪、风和海流的独立散射图中获得疲劳分析的典型海况，必须选择一种结合环境载荷的方法。定义海况的一种可行方法是从波浪散布分块表中选择高占比的典型波浪，并将其与一年一遇的极端海况结合起来。

1.2 计算海况选取

单一海况的占比为ηi，所有海况的占比为η总=∑ηi=100%。为精简计算工况，从海域的海浪统计中筛选出24 个占比较大的典型海况。现假定24 种海况的总比例为100%，对原海况占比进行等比例缩放，即各海况占比为ηi′，ηi′ =ηi/（η总/100%）。以北（N）、东北（NE）、东（E）、东南（SE）几个占比较大的方向为例，调整后的波浪工况占比如表2所示。

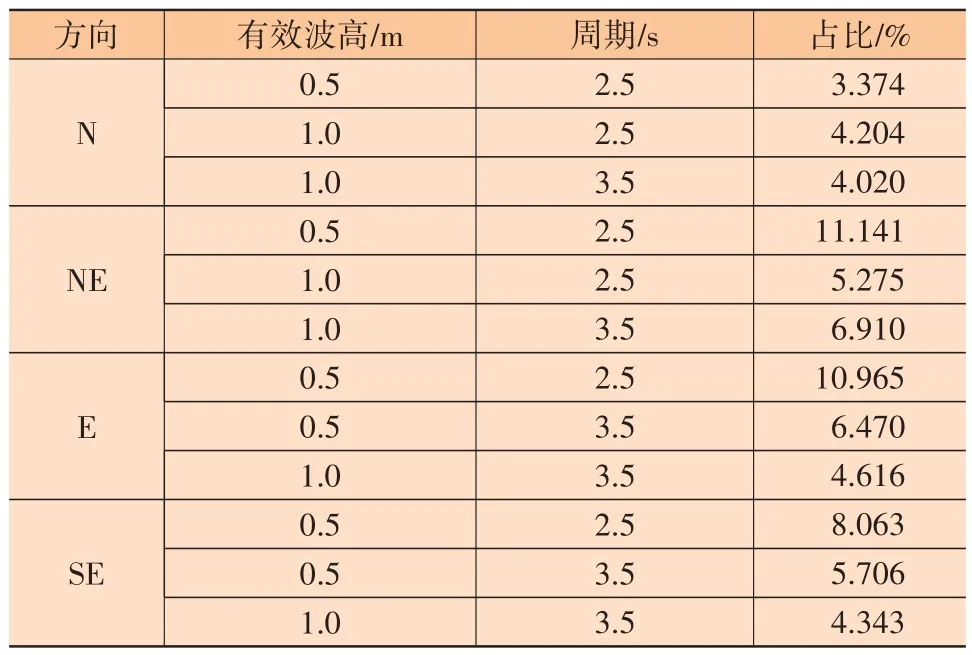
表2 波浪工况占比

2 柔性管总体水动力分析

2.1 柔性管布置情况

由于某平台的大位移，柔性管的疲劳计算与规范检查不匹配。柔性管接头、锚固件、法兰位置的计算疲劳极限较小。经过专家评估和各种方案的比较，决定在底部弯头和四通处使用柔性管代替钢管，以抵消平台大位移造成的不利影响。柔性管布置示意图如图2所示，其柔性管的垂直高度为6 m，并使用弯曲限制器加以节制其弯曲程度，其中EL表示其水平位置（以水面为0位置）。

图2 柔性管布置示意图

2.2 OrcaFlex柔性管模型

参照海管路由位置，利用OrcaFlex软件建立柔性管模型。采用LINE单元，模拟海洋深度为36 m，钢管弯曲刚度及拉伸刚度可以查阅文献选择，但柔性管弯曲等效刚度及拉伸等效刚度一般取决于管材试验，如无试验，则可通过Abaqus 有限元模拟得到，具体数值在下节的参数设置。将表2 中的风浪流载荷参数输入至模型中，设定好边界条件后，进行水动力分析可得到柔性立管所受载荷的时间变化曲线。建立分析模型，其上部的船形部件用来固定钢制立管并定义平台的横向位移数值，以此模拟平台位移与海洋载荷对柔性管的耦合作用。

2.3 参数设置

OrcaFlex 模型为管串，包括钢管、柔性管、弯曲限制器及沙包。其中钢管和柔性管的内、外径为0.136 5 m 和0.273 1 m。柔性管的等效轴向刚度150 kN/m，沙包质量1.0 t，体积0.2 m3。弯曲限制器内、外径为0.24 m和0.5 m，每1 m弯曲限制器质量为0.3 t，抗弯刚度120 kN·m2，轴刚度700×103kN，扭转刚度80 kN·m2。附加质量系数1.0，阻力系数1.2，海床摩擦因数0.5。流速表层1.12 m/s、中层0.88 m/s、底层0.63 m/s。波浪方向为90°，采用不规则波浪谱（JONSWAP谱），设置时间步长为0.1 s，模拟时间为10 800 s。依据平台运动数据，选取平台位移及运动周期，以强制运动的方式施加在平台顶部，平台上部位移幅值为0.1 m，运动周期为5.7 s。

2.4 动态时域分析结果

柔性管的内外压在一般的操作和生产中波动较小[2]，但柔性管由于海洋载荷和自身的重力会产生波动较大的轴向拉伸载荷。柔性管抗拉铠装层一般固定在接头内部的锥体上，在接头连接处的抗拉铠装一般承受最大的拉伸载荷，其显著影响弹性体的疲劳寿命。

轴向力随柔性管长度变化图如图3所示，轴向力在靠近平台上接头最大，在接头连接处的抗拉铠装线承受最大的拉伸载荷，在此提取弯矩和轴向力载荷时程曲线。按照不同工况的波浪和概率，根据所选的波浪工况的周期，将整体时间划分为100 s，按照不同工况下的载荷谱占比，分别提取不同概率对应时长的载荷时程曲线，整合得到整体时长为100 s 的弯矩载荷和轴向力载荷谱，计算其弯矩的数据平均值为17 kN·m，拉伸力数据平均值为23 kN。

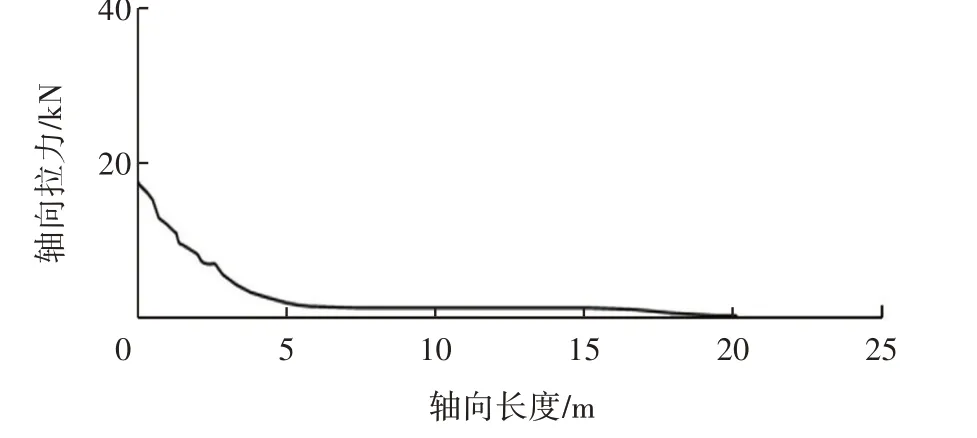
图3 轴向力随柔性管长度变化图

按照OrcaFlex计算得到荷载时程曲线，总时长为100 s对应的不同幅值下的循环次数，弯矩载荷时域曲线图和轴向力载荷时域曲线图分别如图4和图5所示。

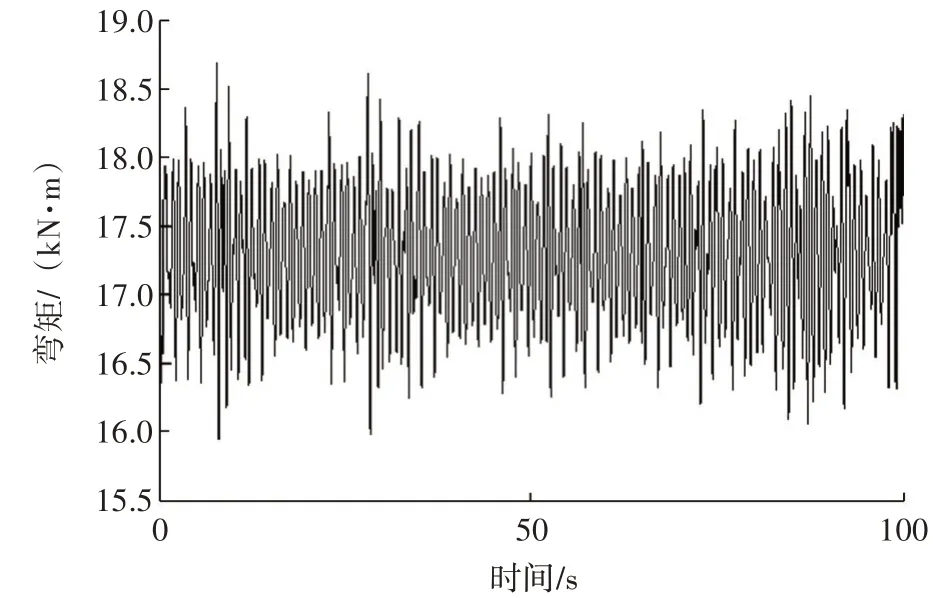
图4 弯矩载荷时域曲线图

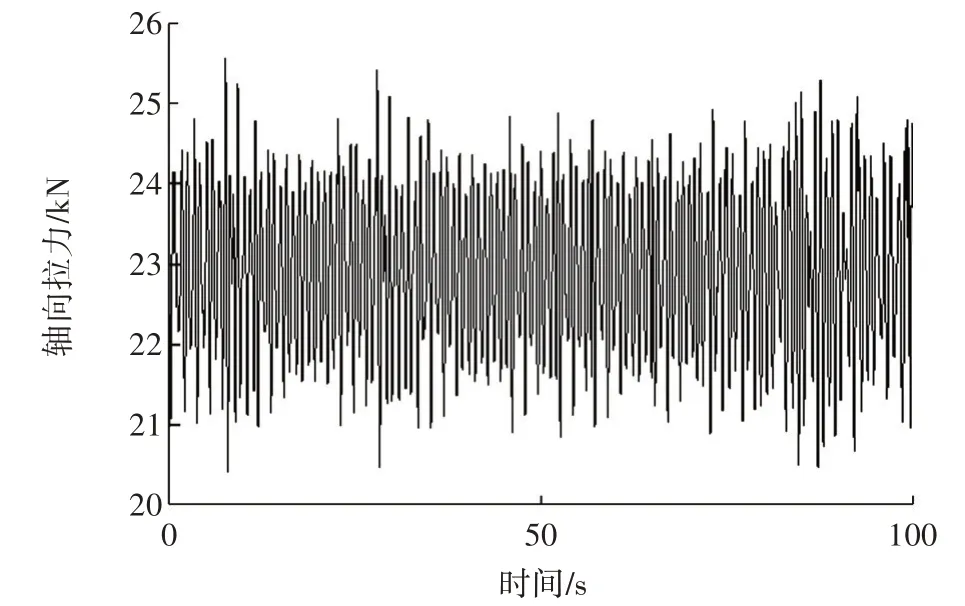
图5 轴向力载荷时域曲线图

依据荷载幅值和平均应力带入柔性管应力计算公式，得到各应力的变化幅值与对应的次数。已知5.5 次循环形成半个周期，则通过统计图的载荷数据，得到弯矩幅值-周期数统计如图6 所示，拉力幅值-周期数统计如图7所示。

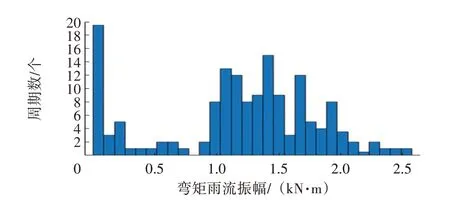
图6 弯矩幅值-周期数统计图

图7 拉力幅值-周期数统计图

3 结束语

本文在某平台立管段的设计中，采用一段柔性管替代钢管的方案，用以减缓由于平台位移过大造成的立管疲劳损伤。采用OrcaFlex 软件对立管模型进行了整体水动力载荷计算分析，对危险点处的弯矩和拉伸力进行了总结分析，分析结果可以用于柔性管的疲劳损伤评估，从而进一步评估危险点处的疲劳寿命。