基尼系数测度贫富差距的一种改进方法
2024-03-16彭妮娅
彭妮娅
(中国教育科学研究院教育财政研究所,北京 100088)
0 引言
我国全面建成小康社会后,开启了全面建设社会主义现代化国家的第二个百年新征程,促进全体人民共同富裕成了新阶段的奋斗目标。减少城乡、区域、群体收入差距是在实现共同富裕过程中需要重点关注的问题,居民收入贫富差距的科学测度是真实了解和有效缩小贫富差距、促进共同富裕的前提。基尼系数是国内外用于测度收入差距的重要指标,基尼系数的定义与洛伦兹曲线围成的面积有关,洛伦兹曲线是累计人口比例对应的累计收入比例组成的曲线,这种构造特征使得两条代表不同收入分配情况的洛伦兹曲线可能有着相同的面积,进而对应着同一个基尼系数值,也就是说,基尼系数无法反映出贫富差距的结构特征,这是基尼系数衡量贫富差距的一个结构性局限。该局限在相关研究中有被提及,但未能得到很好地解决,本文针对此结构性局限,寻求一种改进方法对基尼系数进行适当补充,使基尼系数突破结构性局限的限制,解决基尼系数与贫富差距的非一一对应问题,提升基尼系数衡量贫富差距的准确性。
1 基尼系数的结构性局限
1.1 基尼系数是测度居民收入贫富差距的重要指标
国内外最常用的测度贫富差距的指标是基尼系数。基尼系数在反映居民收入贫富差距方面发挥了重要作用。
图1 横坐标为累计人口比例xi(i=1,2,…,n),纵坐标为对应累计收入比例yi(i=1,2,…,n),n为样本数,且xn=yn=100%。

图1 洛伦兹曲线与绝对平均线
1.2 基尼系数测度贫富差距存在结构性局限
基尼系数的数值和洛伦兹曲线与绝对平均线围成的面积有关。洛伦兹曲线由累计人口比例对应的累计收入比例生成,其曲线形态可以反映出收入差距的大致结构分布,即贫富差距在低收入者之间更明显还是在高收入者之间更明显,或是在中等收入者之间更明显。如下页图2所示,当洛伦兹曲线整体向下凹时(L1),反映的低收入者的贫富差距比其向右凹(L2)时的差距更大。由于洛伦兹曲线L1和L2与绝对平均线围成的面积相同,因此,他们的基尼系数也相同。按通常理解,相同的基尼系数代表的贫富差距相同。而事实上,尽管图2 中L1和L2基尼系数相同,但他们代表的贫富差距情况截然不同,L2代表的贫富差距在高收入人群中更明显,其贫富差距对中低收入者相对友好。L1代表的贫富差距在低收入人群中更明显,其贫富差距对低收入者非常不友好。

图2 基尼系数相等的两条洛伦兹曲线
国家统计局官方网站公布的我国2012—2020年居民人均可支配收入基尼系数变化如图3所示。

图3 2012—2020年我国居民人均可支配收入基尼系数
图3 显示,2012—2020年基尼系数在0.47左右小幅波动,波动幅度仅为0.012,按基尼系数反映贫富差距的通常理解,我国居民收入贫富差距变化不大,甚至在2015年以后有小幅扩大。2020 年我国脱贫攻坚战取得了全面胜利,低收入人群的绝对贫困得到消除,低收入人口收入提升,社会整体贫富差距得到缓解。而这种居民收入贫富差距的实际变化在图3中却未能体现出来,即贫富差距的结构性变化仅通过基尼系数不足以体现。
基尼系数无法反映出洛伦兹曲线蕴含的贫富差距的结构分布,仅通过基尼系数的数值无法反映收入差距主要存在于哪些收入水平的人群中,基尼系数的变化也无法反映收入差距的结构变化,这是基尼系数测度收入差距的结构性局限。在基尼系数无法短时间内明显降低的情况下,让居民的贫富差距情况从图2 中洛伦兹曲线L1向L2移动,是从全面“脱贫”向共同“致富”推进过程中应该努力的方向。
1.3 已有研究未能解决基尼系数的结构性局限
已有文献对基尼系数的测度集中在计算和分解上,而对其结构性局限关注较少。在中国知网搜索“基尼系数局限性”相关主题,发现洪兴建发表于2002年的一篇文章中提到了“相同的基尼系数值可能表示极不相同的收入分配状况”这一不足,并通过“改进标准差系数”来突破基尼系数的局限[1]。但是改进标准差系数的取值与贫富差距程度是何种对应关系,文章没有详细说明。另外。郭平等(2009)[2]认为基尼系数的适用性存在局限,也进行了一些改进方法的探索和应用尝试,但是一些具体方法如系数确定的科学性、适用性等还有待进一步完善。其他有关基尼系数局限性的研究很少提及其结构性局限。
还有学者对基尼系数的计算、收入差距测度、与经济发展的关系等问题做了大量研究,在基尼系数的计算与分解[3,4]、合意值与警戒线[5]、批判与改进[6]等方面为相关研究奠定了基础,其中,基尼系数的分解能提高基尼系数测度贫富差距的精确性。然而对基尼系数进行分解的方法不能弥补其结构性局限。近些年有不少学者又重新开始关注基尼系数基于分组的测算及误差[7],并将基尼系数与洛伦兹曲线进行等价分类[8,9]。但是这些研究都未涉及基尼系数的结构性局限。
首先,对基尼系数进行分组分解的方法依赖于其分组情况,基于同样的样本、不同的分组会得到不同的分解结果。而采取何种分组方式主要取决于主观经验和意愿,缺乏客观的科学依据,现在尚无公认的能提高结果精确性、普遍适用的分组方式。其次,分解基尼系数还达不到反映贫富差距结构的目的。通常只能通过分解及计算得到一个似乎更准确的基尼系数数值,而无法说明其数值为何能更准确地反映贫富差距,也没有证据表明分解计算后的基尼系数值能反映贫富差距的结构变动。最后,提高基尼系数的计算精确度,未能涉及基尼系数测度贫富差距的结构性局限产生的本质原因:代表不同贫富差距情况的两条洛伦兹曲线可能对应着同一个基尼系数。因此,仅依靠提高基尼系数计算的精确度,无法突破其结构性局限,应从局限产生的原因,即洛伦兹曲线的构造上入手。本文拟从基尼系数测度贫富差距的结构性局限上入手,针对不同的洛伦兹曲线对应同一基尼系数的情况,研究改进方法,提高基尼系数对贫富差距结构的反映度。
2 对基尼系数结构性局限的改进
2.1 基尼系数结构性局限产生的原因
因为代表不同贫富差距的洛伦兹曲线可能对应同一基尼系数(如图2所示),所以基尼系数与贫富差距情况不具有一一对应性。我国脱贫攻坚战取得的巨大成就表明,基尼系数不变或变化小,不意味着居民收入的贫富差距没有变化,其贫富差距的结构性特征无法仅依靠基尼系数反映。因此需要寻找一种测度方法对基尼系数进行补充,共同反映在基尼系数变化不大的情况下,贫富差距结构的变化情况。
洛伦兹曲线是累计人口比例对应的累计收入比例,其表示人口每增加1 个百分点,收入增加了几个百分点,可以看作是收入由低到高排列的人群的收入变化速度。如下页图4 所示,在洛伦兹曲线上任取两点P1(x1,y1) 和P2(x2,y2),过两点分别作切线T1(x)和T2(x),将切线斜率记为k,(x2,y2)。当x从0 变化到1 时,其切线斜率逐渐增大。由于T1的斜率小于T2的斜率,因此P1表示的人口每增加1%对应的收入增加的百分比小于P2,即P1的收入增加速度小于P2。

图4 洛伦兹曲线上点的切线变化
2.2 用平均增长点改进基尼系数的结构性局限
当洛伦兹曲线上某点的切线斜率为1时,表示该点的人口增加和收入增加速度相等,即人口增加1%,收入也增加1%,此时收入是“平均增长”的,该点代表的贫富差距是公平的。可以将洛伦兹曲线上切线斜率为1的点叫做“平均增长点”。
绝对平均线上的每个点都是平均增长点,每条洛伦兹曲线有且仅有一个平均增长点。基尼系数相同的不同洛伦兹曲线,由于其贫富差距结构不同,且洛伦兹曲线切线斜率具有单调性,其平均增长点对应的横坐标x值必然不同。于是可以通过比较等基尼系数的不同洛伦兹曲线的平均增长点x值,分析相同基尼系数的不同贫富差距结构。
基尼系数相同但是曲线形状和贫富差距结构不同的洛伦兹曲线,可以称为“等基尼系数线”,一组等基尼系数线和一个基尼系数对应。当基尼系数不同但相近时,根据平均增长点的含义,也可以引入平均增长点,与基尼系数相结合,共同测度贫富差距,突破单纯依靠基尼系数测度贫富差距的结构性局限。
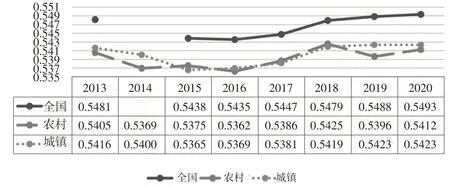
如图5所示,假设有基尼系数相同的三条洛伦兹曲线L1、L2、L3,分别做平行于绝对平均线的三条切线,切点的横坐标值分别为x1、x2、x3,可见,x1 图5 等基尼系数线的平均增长点比较 根据居民收入分配情况(通常是五分法)可以计算出基尼系数,也可根据离散数据拟合出曲线函数并求导。根据洛伦兹曲线形状和可导性,可对洛伦兹曲线进行二次函数拟合,设L(x)=ax2+bx+c(a>0 ),a、b、c是常数,常数特性可根据曲线特征进一步讨论,令L'(x)=2ax+b=1,求解出的即为平均增长点的值,将洛伦兹曲线L的平均增长点记为xA(L)。 国家统计局公布的全国居民五等份收入数据,是将所有调查户按人均可支配收入水平从低到高排列,分为五个等份,依次记为低、中下、中等、中上、高收入五组。假设某年的居民五等份人均收入值分别为x1,x2,…,x5,可算出五组的累计收入占比,i=1,2,…,5,其中,y5=1。如图6所示。 图6 根据收入五等份数据拟合洛伦兹曲线 收入五等份数据拟合的洛伦兹曲线如图7至下页图9所示。各洛伦兹曲线的二次函数的拟合优度R2均高于0.99,拟合优度非常好。2014年全国数据缺失中等收入及高收入组人均可支配收入数据,无法计算当年全国基尼系数。 图7 城镇居民五等份人均可支配收入的洛伦兹曲线 图9 全国居民五等份人均可支配收入的洛伦兹曲线拟合 根据基尼系数的定义,G=2SA=1-2SB。区域B的面积通常有两种计算方法:一是离散替代法,近似为一个三角形和若干个梯形的面积之和,图6 中,,其中n是等份组数,且n越大,二者越接近[3];二是拟合洛伦兹曲线法,求曲线L(x)从0到1的定积分。由于五等份的分组数较少,精确性不能保证,因此,为了提高计算精确性,本文采用拟合曲线法。设L(x)=ax2+bx+c(a>0 ),则: 根据居民五分法收入数据拟合出的各年份洛伦兹曲线ax2+bx+c的系数如表1所示。 表1 城镇、农村、全国居民可支配收入的洛伦兹曲线拟合系数 进而根据式(4)计算出各年份的基尼系数,如图10所示。 图10 基于居民收入五分法拟合洛伦兹曲线计算的基尼系数 由于统计口径、样本量等存在差异,因此根据五分法计算的基尼系数低于统计局公布的基尼系数,但是,其反映的全国、城镇及农村三个维度之间基尼系数的关系符合普遍认知,整体变化趋势也与国家统计局的数据一致,可以用来进行进一步分析。 拟合出洛伦兹曲线后得到二次曲线函数表达式,并根据式(2)计算出各年洛伦兹曲线的平均增长点,如图11所示。 图11 居民收入五分法拟合洛伦兹曲线的平均增长点 基尼系数对贫富差距而言是正向指标,即基尼系数越大,贫富差距越大;而平均增长点对贫富差距而言是负向指标,即平均增长点越大,贫富差距对低收入人群越友好,整体贫富差距越小。于是可构建一个将基尼系数和平均增长点合二为一的二元数组(G(L),xA(L))。假设两种贫富差距情况对应的洛伦兹曲线分别为L1和L2。 情况1:当G(L1) 情况2:当G(L1) 其中,α、β待定。若>xA(L2),则L1的收入分配较优,L1的贫富差距小于L2;若 根据居民收入五分法计算的2013—2020年全国维度基尼系数在小幅波动中基本保持稳定,在2018 年达到研究期间最大值0.3897后,下降至2020年的0.3848,跟2013年基尼系数0.3883 相比,降幅很小。同样地,农村维度基尼系数先升后降,在2018 年达到研究期间最大值后下降到略高于2013 年的水平,波动幅度比全国维度大。而城镇维度的居民收入基尼系数变化情况有所不同,呈先降后升的趋势,2015年达到最小值,2018年回升至与2013年基本持平的水平后继续上升,2020年达到最大值。 仅依靠基尼系数来判断居民收入差距情况,可从两个方面进行:一是群体的横向比较,二是纵向变化。从横向比较来看,全国范围的收入差距大于农村地区或城镇地区的收入差距,农村地区的收入差距大于城镇地区收入差距。前者由于农村或城镇样本包含于全国内,因此全样本的差距大于部分样本的差距;后者由城乡二元结构导致,这与大家通常的认知一致。从纵向变化来看,全国的收入差距略微扩大后回落,变化很小;农村的收入差距先扩大后缩小,最终小幅增加;城镇的收入差距先缩小后扩大。 结合平均增长点则可反映出更多信息:从2013 年和2020 年来看,全国、农村、城镇三个维度的平均增长点都有所增大,说明收入差距在向变小的方向发展。以城镇地区2018年和2019年为例,两年的基尼系数都是0.3132,若仅依靠基尼系数判断收入差距,则可以说这两年城镇地区居民的收入差距未发生变化,而结合平均增长点可知,其从0.5419 增加到0.5423,虽然变化不大,但其反映了收入差距缩小和贫富差距向更公平的状态变化的趋势。2013—2020 年,平均增长点反映出我国居民收入差距先略微扩大后明显缩小,2020 年居民收入差距情况整体优于前些年,且全国、农村、城镇三个维度均是如此。 本文针对基尼系数的结构性局限,从统计测度方法上进行改进,用“等基尼系数线”概念表示一组基尼系数相同但是形状不同且代表不同贫富差距的洛伦兹曲线。等基尼系数线表示的是两条(或以上)洛伦兹曲线之间的关系。从等基尼系数线的平均增长点间的比较延伸至基尼系数相近的洛伦兹曲线间的比较,可将相关方法运用到所有基尼系数的贫富差距结构比较上。同时,“平均增长点”可以弥补基尼系数和洛伦兹曲线的非对应问题。用每条洛伦兹曲线有且仅有一个平均增长点,且其表示收入差距平均变化的特点,将基尼系数和洛伦兹曲线非一一对应的问题,转换成基尼系数与平均增长点组合后和洛伦兹曲线一一对应的情况,突破基尼系数测度贫富差距的结构性局限,将基尼系数测度贫富差距的非唯一性变成唯一性。从统计学方法上提升测度的科学性。 测度方法的改进亦对研究观点有一定影响,通过对基尼系数的构造研究可知,在共同富裕背景下研究贫富差距,应重点关注低收入人群的收入差距对社会整体贫富差距的影响。对社会贫富差距起决定性作用的是低收入人群的收入及其与高收入人群之间的差距,高收入人群之间的收入差距对社会整体的贫富差距不起决定性作用,缩小贫富差距在根本上要靠“提低”,而非“限高”。缩小贫富差距、促进共同富裕的根本在于提高低收入人群的收入,扩大中等收入群体,使收入分配从“穷人很穷,富人不富”向“穷人不穷,富人很富”转变。 未来研究可从本文的一个难点入手,即二元测度方法中的系数的合理确定。在二元测度方法(G(L),xA(L))的换算中,,要研究不同的系数α、β对测度结果的影响,寻找科学的方法确定系数α、β的值,使结果能更准确地反映贫富差距,以突破基尼系数的结构性局限,同时又具有科学性和广泛适用性。
3 改进方法的应用
3.1 根据居民可支配收入五分法数据计算基尼系数


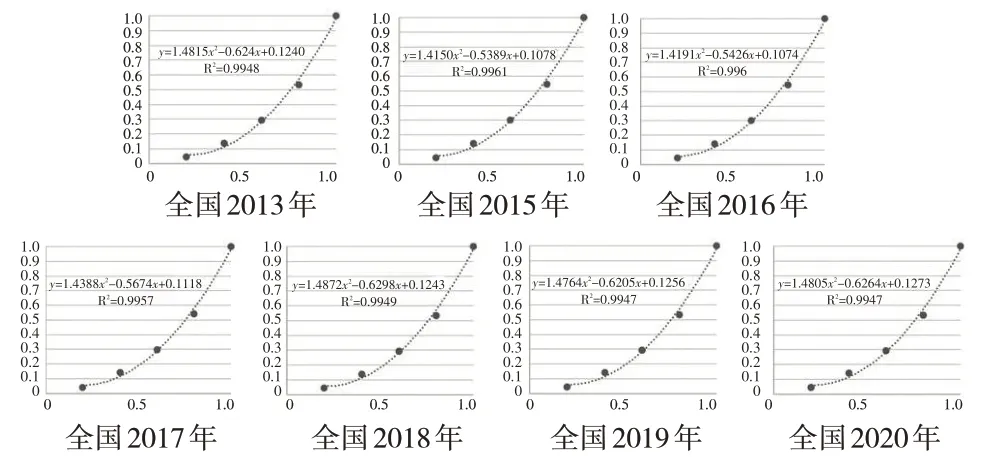


3.2 平均增长点和基尼系数共同测度贫富差距
3.3 实证结果分析
4 结论与展望
4.1 结论
4.2 展望
