基于改进灰狼算法的宏微复合驱动器磁滞模型的参数辨识*
2024-03-15喻曹丰陶雪枫魏益军
喻曹丰 陶雪枫 魏益军 杨 坤 王 宁
(①安徽理工大学机电工程学院,安徽 淮南 232001;②流体动力基础件与机电系统国家重点实验室,浙江 杭州 310027)
高新工业科技的不断发展使得高精度定位跟踪技术成为工业界和学术界的研究热点,具备大行程、高定位精度的驱动器及其建模控制越发成为精密定位领域的重心[1]。传统单级驱动装置因其结构限制,较难同时实现高精度和大行程特性,针对这个问题,本文提出宏微复合驱动装置的思路,即宏动部分满足大行程位移功能,微动部分负责实现高精度跟踪定位要求[2-3]。宏微复合驱动方式主要有两种,即堆栈叠加式(微动台堆叠于宏动台之上)和同轴对中式(微动台与宏动台在同一轴线上)。堆栈叠加式对位移的测定存在偏差,严重影响定位精度;而同轴对中式结构保证了宏动与微动之间的轴线对齐[4],有效避免了这种问题。根据上述情况,本课题组将超磁致伸缩驱动器和音圈电机紧密结合,提出了集高速度、大行程和精密特性于一身的同轴集成式宏微复合驱动器,并搭建了试验平台。该方案将宏动部分与微动部分集成在同一体中,避免了安装时不能保证轴线对齐的问题,同时也降低了堆栈叠加式中的阿贝误差,提高了定位精度[5]。
作为微动台负责实现短行程精密定位的超磁致伸缩驱动器,超磁致伸缩材料(GMM)为核心部件,具有小体积、高能量转换率和快速响应等优点。但由于GMM 存在磁滞非线性现象,严重影响了GMA 的实际应用。因此要想提升超磁致伸缩驱动器的定位精度与控制效率,关键在于精确地构建其位移输出模型。1935 年,经典Preisach 模型被提出,但模型会产生大量非物理参数,使得建模和控制过程较为复杂[6]。PI 模型主要通过加权叠加磁滞算子来描述铁磁材料的磁滞非线性,但该模型对铁磁材料的特性要求较高,因此很难满足建模条件[7]。基于铁磁畴壁理论构建的Jiles-Atherton(J-A)模型,是一种具备物理磁滞特性的模型,探讨了铁磁材料磁化强度与磁致伸缩的耦合作用,揭示了磁化过程机理[8-9]。但J-A 模型中参数互相耦合,在实际应用中辨识较为困难。王珊珊运用粒子群算法对J-A 模型进行了分段的参数辨识与寻优,得到最优参数组合[10]。另外,刘慧芳将遗传算法与模拟退火算法融合,进行GMA 磁滞非线性模型的参数辨识[11]。
针对GMA 磁滞非线性模型中的J-A 模型参数辨识,一直缺乏能高效逼近参数真实值的算法。本文提出基于3 种改进策略的灰狼优化算法,采用Singer 混沌映射更新灰狼个体的初始位置,同时引入非线性控制因子策略、自适应位置更新和动态权重更新策略,可有效改善传统灰狼算法寻优后期易陷入局部最优及求解精度不高的缺陷。仿真实验表明,提出的TGWO 算法具有更强的寻优求解能力,辨识结果逼近非线性磁滞模型参数真实值。
1 同轴集成式宏微复合驱动器结构及数学模型
1.1 同轴集成式宏微复合驱动器结构
同轴集成式宏微复合驱动器宏动部分主要由磁轭、永磁体、结合架等组成。6 个永磁体产生宏动磁场,宏动线圈通电后在磁场作用下带动驱动器整体进行位移,实现大行程功能。微动部分由超磁致伸缩材料(GMM)棒、微动线圈、隔磁筒等组成。宏动部分定位完成后,微动线圈通电产生微动磁场,GMM 棒在磁场作用下伸长产生位移,补偿宏动部分位移跟踪误差。
实验平台如图1 所示。

图1 同轴式宏微复合驱动器结构示意图
1.2 宏微复合驱动器微动部分的位移磁滞非线性模型
铁磁材料J-A 磁化理论模型中,磁化强度M与外加磁场H之间的关系如下:
式中:He为磁性材料的有效磁场;H=nI为外加磁场;α为铁磁材料畴壁相互作用系数;a为铁磁材料的形状系数;Man为铁磁材料的无磁滞磁化强度;Ms为饱和磁化强度;Mrev为可逆磁化强度;Mirr为不可逆磁化强度;δ为符号常数,当dH/dt<0 时,δ=-1;dH/dt>0 时,δ=1;k为不可逆损耗系数;c为可逆分量系数。δM为去除负磁化系数的参数,表示为
磁场作用下超磁致伸缩棒的磁致伸缩系数λ及伸长量ΔL为
式中:λ为铁磁材料的磁致伸缩系数;λs为饱和磁致伸缩系数;ΔL为超磁滞伸缩棒的伸长量;L为GMM 棒原长。式(1)和式(3)构成了宏微复合驱动器微动部分的位移磁滞非线性模型,由输入电流I可得到微动部分的输出位移。在非线性磁滞模型中辨识5 个参数,为θ=(Ms α a k c)。
2 TGWO 算法
2.1 标准灰狼算法
灰狼优化(grey wolf optimization,GWO)算法主要通过模拟野外狼群社会的等级制度和捕猎形式实现优化搜索的目标[12]。GWO 算法将最优目标解设为α狼,次优解设为β狼,第三优解设为δ狼,由它们来领导狼群追捕猎物;所有其他解定义为γ狼。算法中灰狼追捕猎物行为分为四散包围、展开追捕与进行攻击。狼群四散包围猎物如下:
式中:D为灰狼与目标之间的距离;Xk(t)和Xp(t)为优化算法迭代t次后第k只灰狼和目标猎物的位置;A和C为干扰因子。当|A|≤1 时,狼群展开追捕,强调局部开发;|A|>1 时,狼群放弃追捕并继续向外散开,突出全局寻优。A和C的计算公式如下:
式中:r1、r2为[0,1]间随机产生的向量;a为收敛因子,由式(6)可知其值随灰狼算法迭代次数的增加而递减。
式中:T为最大迭代次数。
灰狼个体追捕猎物位置的公式表达如下:
式中:Dα、Dβ、Dδ为α狼、β狼和δ狼与种群其他灰狼之间的距离;Xα(t)、Xβ(t)、Xδ(t) 为α狼、β狼和δ狼的所在位置。
在追猎阶段,其余的γ狼向着α狼、β狼和δ狼的跟随前进:
其中灰狼个体位置的迭代更新公式如下:
2.2 Singer 混沌映射
标准 GWO 算法产生的初始种群具有随机性,可能分布不均使得种群多样性差。文本采用的Singer 映射作为经典混沌映射,具有长期不可预测、整体稳定等特性,生成的混沌序列具有普适性和分数维持性等特征[13],其数学表达形式为
其中:λ∈[0.9,1.08]。
生成的序列sk∈[0,1],用来更新GWO 种群的初始位置Xk,如下式所示:
其中:ub与lb为种群空间的上边界与下边界。
2.3 非线性收敛因子
标准GWO 算法通过添加收敛因子a更新位置公式里的参数A,从而平衡算法的全局搜索与局部开发能力。传统灰狼算法中收敛因子a线性递减的更新策略使其跳出局部最优值的能力较差,严重削弱了算法全局求解能力。因此本文采用基于Sigmoid函数结构[14]的非线性收敛因子更新公式:
式中:abegin和afinal为收敛因子的起始值2 和终值0;t为迭代次数;T为最大迭代次数。
相较于传统GWO 算法的线性递减策略,本文采用的非线性收敛因子使得算法前期保持大步长全局寻优,且速度相对较慢,保证种群多样性的同时增强了全局寻优能力;中期提升寻优速率;后期小步长搜索,速度相对变缓,提升算法的局部开发能力和求解能力。
2.4 引入动态权重与自适应更新策略
传统GWO 算法通过求X1、X2、X3平均值的方式更新种群位置,无法凸显α、β、δ三者之间的重要性,因此本文引入了基于修订动态权重的位置更新策略[15]。
当前灰狼个体到α、β、δ之间的距离权重:
同时,为了增强算法的全局搜索和局部开发能力,本文提出了一种效果更好的自适应位置更新方法。最终的灰狼位置更新方程为
3 基于TGWO 算法的磁滞模型参数辨识
3.1 辨识算法流程图
综合以上算法优化策略,设定改进灰狼算法的步骤。
步骤1:设定种群规模大小N、目标空间维度D、总迭代次数T、常数ε;初始化a、A、C。
步骤2:采用Singer 映射更新种群初始化位置。
步骤3:计算种群灰狼个体的适应度值,挑选出前三优解设为Xα、Xβ和Xδ。
步骤4:更新种群中其他灰狼的位置。
步骤5:更新非线性收敛因子a,确定a之后更新干扰因子A和C。
步骤6:判断算法是否满足结束条件,若满足,输出最优解并结束算法;否则,重复执行步骤3 至步骤5。
3.2 参数辨识原理
宏微复合驱动器微动部分磁滞非线性模型参数辨识原理如图2 所示。基于最小二乘法原理建立参数辨识的目标函数并求解极小值:

图2 参数辨识原理图
式中:R为采样次数;k为第k个采样时刻;y(k)为位移测量值;为模型位移计算值;θi为θ的第i个参数;ai、bi分别为 θi的下限与上限。
4 辨识结果与实验验证
4.1 实验数据测量
宏微复合驱动器实验平台如图3 所示,主要包括精密程控电源、高精度位移传感器、功率放大器和宏微复合驱动器。驱动器关键部件GMM 棒尺寸为ϕ8×80 mm。以5 A 为最大工作电流Imax,步长为0.2 A,测量电流由0 增加到Imax再减小到0 的GMM棒伸长量。

图3 实验平台实物图
4.2 数值仿真
设定种群规模p=100,最大迭代次数T=150。采用传统灰狼算法和TGWO 算法分别进行3 次参数辨识,如图4 和图5 所示,参数辨识结果见表1。结果表明传统灰狼算法在求解目标函数值时,会出现早熟和停止现象,易陷入局部最优解;同时辨识结果中个别参数出现撞击边界的情况。而TGWO算法拥有更高的稳定性和全局收敛能力,能更好地脱离局部最优,使辨识目标快速地向全局最小值收敛。经过150 代运算目标函数值达到0.462,相比于传统灰狼算法只收敛到2.146 有了较大提升。

表1 参数辨识结果

图4 传统灰狼算法
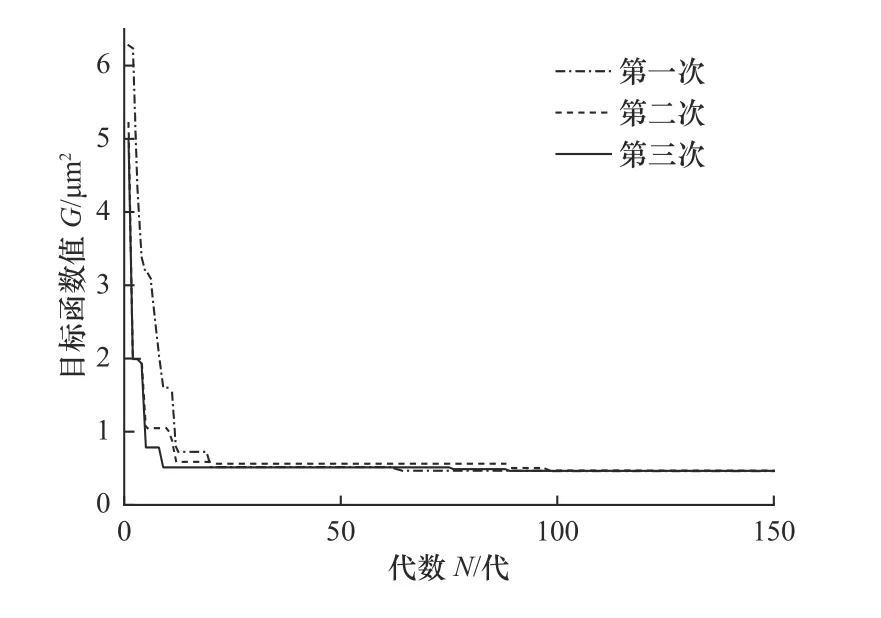
图5 TGWO 算法
分别利用传统灰狼算法和TGWO 算法辨识出的结果计算复合驱动器GMM 棒的伸长量,并与实验数据比较,结果如图6 所示,平均相对误差分别为9.8%和4.6%。因此,TGWO 算法的计算结果与实验结果符合程度更高,辨识出的参数更逼近真实值。
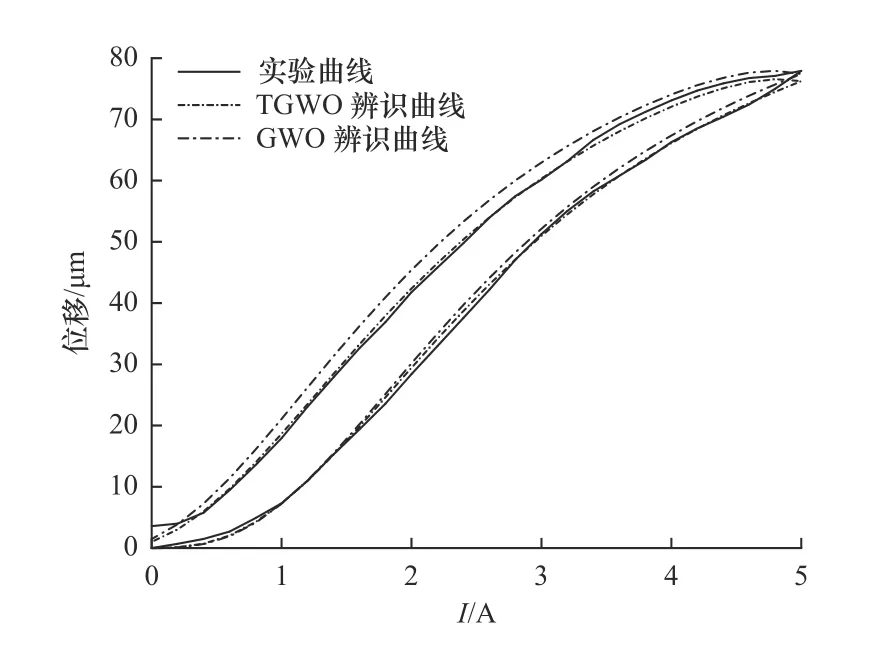
图6 仿真结果与测量结果比较
为了检验任意变化趋势的输入电流控制下,利用优化算法辨识结果计算GMA 位移的准确性,本文改变输入电流的幅值进行仿真,电流最大值取4 A 和2.4 A,并与实际测量数据做对比,结果如图7和图8 所示。电流幅值为4 A 时,传统灰狼算法与TGWO 算法计算结果平均误差分别为7.9%和4.5%。电流幅值为2.4 A 时,传统灰狼算法与TGWO 算法计算结果平均误差分别为7.3%和4.2%。由此可见,TGWO 算法的辨识结果能更好地反映参数真实值,位移计算值与实际测量值吻合程度更高,可以用作位移模型的计算。
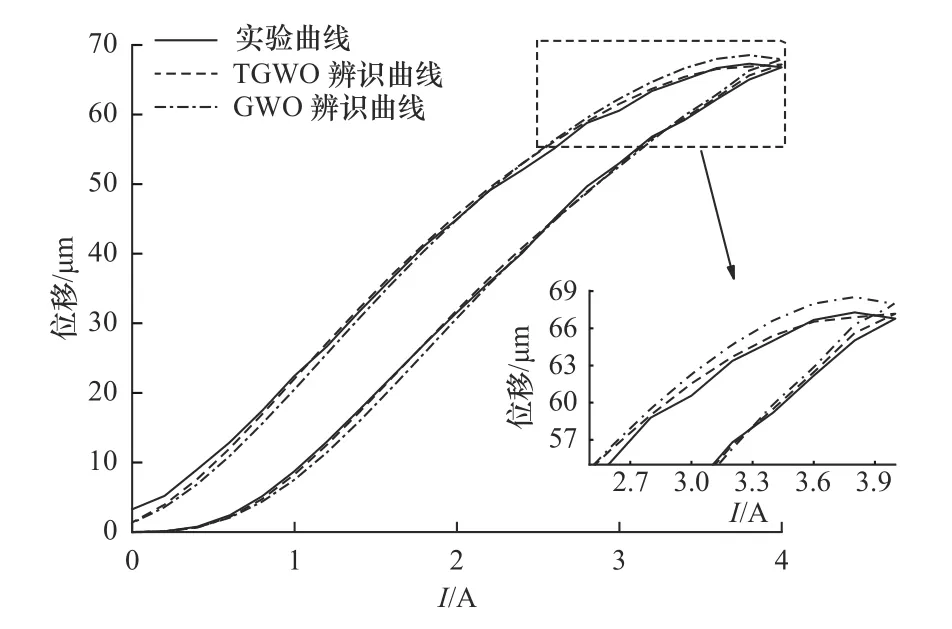
图7 电流幅值为4 A 时仿真结果与测量结果比较

图8 电流幅值为2.4 A 时仿真结果与测量结果比较
5 结语
(1)本文所提出的TGWO 算法在传统灰狼算法的基础上,引入混沌映射、非线性收敛因子、修订动态权重和自适应更新位置策略;有效抑制了GWO 算法全局收敛难、易陷入局部最优及参数易撞击设定边界的缺点,提高了辨识精度和最优解质量。
(2)经过多次辨识计算证明,改进后的算法求解效果较好。电流幅值为5 A 时,三次仿真GMA 模型位移计算值与测量值平均误差分别为4.68%、4.62%、4.65%;电流幅值为4 A 时,平均误差为4.52%、4.46%、4.48%;电流幅值为2.4 A时,平均误差为4.11%、4.25%、4.16%。因此,算法辨识参数可以应用于后续驱动器的建模控制。
