基于逆向工程的小型钻床立柱结构优化
2024-03-15汪栋成刘淑莲陈岁繁
汪栋成 王 宇 刘淑莲 陈岁繁
(浙江科技大学机械与能源工程学院,浙江 杭州 310023)
随着科技的进步和制造业的快速发展,传统的经验和类比设计方法不再满足高精度、高可靠性、轻量化的设备制造要求。数理统计和有限元的分析方法逐渐成为设计和验证模型的主要凭证。
立柱作为机床的核心部件之一,在传统经验设计下,往往存在一定的质量冗余情况,其动静态特性更能直接决定机床整体工作的稳定性,因此对其进行力学性能分析、减轻质量具有重要的现实意义[1]。仇君等[2]通过对立柱加载分析说明钻削力经由主轴箱传递具有更高的准确性,同时利用选型法提高其静态性能,减轻质量。董斌等[3]通过力学分析找到机床工作的立柱薄弱环节,采用响应面优化方法,以提升立柱前两阶固有频率为主要目标,完成尺寸优化。蒲凡等[4]运用多目标拓扑优化辅助立柱结构合理布局,提高其动静态特性。李源等[5]采用多级优化方法,完善立柱从概念到详细设计的过程。
但以上文献机床结构模型主要来源于图纸,与实际工件尺寸存在一定误差。基于此,将逆向工程技术引入参数化结构优化存在工程意义。逆向工程(reverse engineering,RE)是指通过一些基本的测量手段,从已经存在的产品模型,反向推出设计数据的过程[6]。闫磊等[7]使用手持式激光扫描仪获取支架零件三维数据,再通过有限元分析优化结构,完成重构模型的快速再设计。周小东等[8]采用正逆向建模将连杆结构重建,并在Workbench 中完成参数优化。仇灿华等[9]通过提取手柄点云数据特征曲线构建曲面,完成实体模型重建,并在有限元色阶图中找到手柄最大应力区域。但以上逆向工程运用都是针对特定工件的,在结构优化方面存在一定经验性且流程并不完整,或只是借助逆向模型进行简单分析,缺少优化流程。
本文通过三维扫描采集实体机床零部件数据,运用逆向建模技术将模型重新组装,采用静力和模态分析对机床结构进行研究,并在此基础上选取合适的优化方法实现立柱结构轻量化。该方法将逆向工程中参数化建模和有限元中参数化结构优化设计相结合,为产品改进和再设计提供完备的工艺流程,对逆向工程集成应用有一定借鉴意义。
1 模型三维重建
1.1 数据采集
在逆向工程的测量方法中,按是否需要与被测物体接触,分为接触式和非接触式两大类。接触式测量速度慢、设备昂贵,且难以应对结构复杂的物体表面。结构光三维扫描作为非接触式测量的一种,通过光学原理获取被测物体三维信息,因具有无损耗、高精度和高效率的优势被广泛应用。
考虑到机床表面曲率变化较多、结构较为复杂,本文使用上海数造3DSS 幻影四目形三维扫描仪,对上海某机床公司小型钻床整体进行数据采集。
对于钻床结构零件而言,由于相机感光元件动态范围有限,在三维扫描时,摄像头接收的图像会因为金属物体表面的粗糙度、材质以及形状等因素,出现局部亮度饱和现象,导致成像点云不完整。为避免上述现象,使用显像剂均匀喷涂物体表面,尽可能将其表面反射性质转变为漫反射,以减少三维成像数据的缺失。在钻床结构零件上贴上合适位置、数量的标记点,多角度、反复扫描,同时在仪器配套软件中进行点云粗配准,依据配准误差筛选出合适的点云数据,如图1 所示。

图1 三维数据采集
1.2 数据处理
1.2.1 数据预处理
实验扫描采集的数据为.gpd 格式,其形貌是由许多三角面片组成的多边形网格,存在自相交、高度折射边、非流形边等问题。使用Geomagic Wrap软件对以上问题进行修复。通过连接点对象、删除体外孤点、封装、去除钉状物、减少噪音、快速光顺以及孔洞填补等操作步骤进行数据初步处理,如图2 所示。

图2 立柱数据预处理
1.2.2 逆向建模
模型原件的重构是关键环节,其方法是通过逆向建模将Geomagic Wrap 预处理后的.stl 格式文件转换为实体模型,以便后续的工程性能分析应用。本文使用Geomagic Design X 软件,通过领域划分、坐标系对齐、草图编辑、拉伸、放样、剪切和缝合等操作步骤进行逆向建模。模型草图编辑和立柱实体分别如图3 和图4 所示。
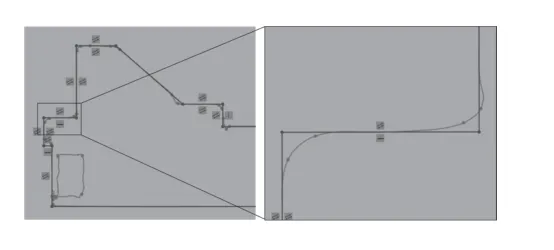
图3 轮廓投影草图编辑

图4 立柱实体模型
将立柱.stp 格式实体和.stl 格式点云导入Geomagic Control X 软件,通过2D 比较得到立柱实体轮廓和点云数据之间的偏差,如图5 所示,直线上的最大偏差在0.8 mm 左右,整体平均偏差为-0.050 9 mm。考虑到立柱实物表面并非完全工整且拐角处存在倒角弧度,认为平均偏差在-0.1~0.1 mm,对有限元分析结果影响较小,满足工程分析模型精度要求。
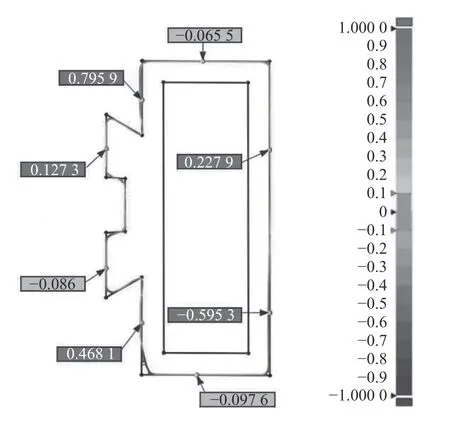
图5 立柱2D 偏差分析
重复数据处理步骤,对机床各个零件实体逆向建模,其关键部件模型及实物如图6 所示。由于数据采集过程中图像拍摄角度存在一定限制且部分结构会造成光线遮挡,对于缺少的尺寸参数,利用卡尺实物测量进行数据补全。考虑到主轴箱是由多个部件拼接而成的,部件间存在一定缝隙且主轴箱右半边包裹的电子元件对实验影响较小,逆向模型为其简化后的结果。通过SolidWorks 软件制作装配体完成机床整体模型搭建,如图7 所示。将机床装配体保存为.x_t 格式用于工程性能分析。

图6 机床零部件实物及模型

图7 机床实物与模型装配体
2 有限元仿真
2.1 机床加载与分析
将.x_t 格式机床三维模型导入Ansys 软件,为确定立柱在极端工况下的性能,将机床主轴箱推至产品说明书强调的最危险工作位置。
定义床身、立柱、工作台、主轴箱和夹具结构材料为HT250,滑块、主轴结构材料为45#钢,材料具体参数见表1。设置机床底部螺栓处为固定约束,其余零部件连接处设置绑定接触。对机床整体进行自适应网格划分,几何体尺寸调整为10 mm,得到节点个数为162 016,单元个数为90 632,其有限元网格模型如图8 所示。
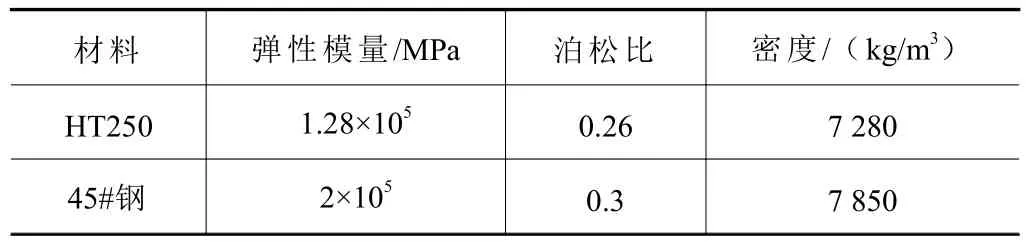
表1 材料属性

图8 机床有限元网格模型
2.2 静力分析
静力学是模型结构有限元分析的基础,对机床整体进行静力分析,可以找出系统中应力、变形量最大的位置,为之后的改进和优化提供依据。
考虑到机床立柱所受载荷主要为主轴箱传递的钻削力和机床自重,对机床整体施加标准重力加速度,同时在刀头夹具上添加钻削力与钻削扭矩,计算刀具为高速钢、工件材质为多相合金时的钻床受力情况。
钻床钻削力和钻削扭矩计算公式为
式中:T为钻削扭矩,N·m;Pk为钻削力,N;D为钻头直径,mm;ƒ为每转进给量,mm/r;Kp为修正系数。
将相关参数代入计算公式计算可得:
根据以上约束条件和载荷,对机床整体进行静力分析,得到形变量云图和应力分布云图,如图9和图10 所示。
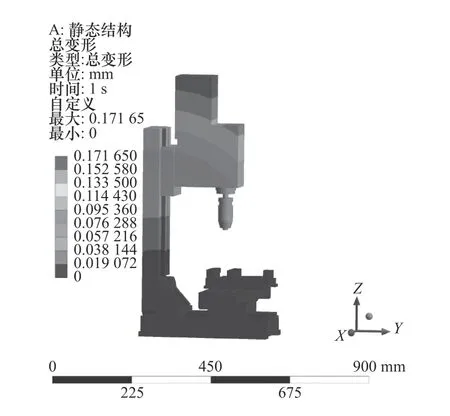
图9 机床形变量云图

图10 机床应力分布云图
由图9 和图10 可知,机床在工作状态下,形变量发生变化的位置集中于主轴箱和立柱,其中立柱是应力变化的主要承担对象,决定机床工作的稳定性。因此,机床的动静态性能研究主要关注立柱的结构特性,图11 和图12 分别为形变量云图和应力分布云图。

图11 立柱形变量云图

图12 立柱应力分布云图
由静力学分析结果可知,立柱最大应力值为7.554 7 MPa,最大形变量为0.113 72 mm,立柱最大形变集中在立柱顶部。这是由于立柱顶部距离固定约束最远,形变量由上至下逐渐减小,符合立柱的结构特点和实际受力情况。从应力云图来看,最大等效应力远小于灰铸铁的强度极限250 MPa,且应力主要集中于导轨的中下部分,结构设计趋于保守,材料分配还可以进一步改善。
2.3 立柱模态分析
模态分析可用于确定模型结构的固有频率与相应振形。为防止该产品在工作中发生共振,在圆孔位置设定固定约束,求解前6 阶固有频率,结果见表2。

表2 立柱模态分析结果
从模态分析结果得出立柱的1 阶固有频率为148.97 Hz,频率较低。在外部激励引发立柱共振时,会发生17.895 mm 的最大变形,对机床加工精度产生较大影响,有必要通过提高其固有频率改善模型动态性能。立柱1 阶振形如图13 所示。
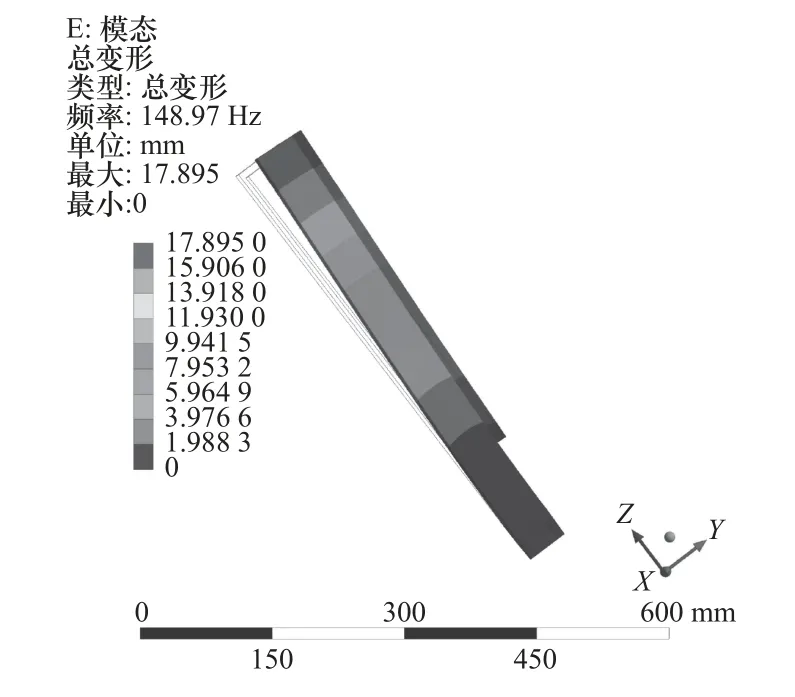
图13 立柱1 阶振形
3 立柱结构优化
3.1 立柱形状优化
拓扑结构优化可快速获得满足要求的模型形状。本文采用变密度法进行拓扑优化,该方法将材料密度假想在0~1,通过确定单元相对密度为0 或1 决定是否被删除,从而求解结构材料的最佳分布。非优化区域位置选择立柱导轨结构,综合目标设置为柔度最小和低阶模态最大,权重分别为0.4 和0.6,响应约束为去除10% 质量。通过迭代仿真计算得到拓扑优化密度云图,如图14 所示。其中深色区域为建议去除区域,主要分布于立柱上端面、背面、侧面;浅色区域为可调节区域,分布于前面、侧面、背面和底部连接处;白色区域为计算结果保留区域。

图14 立柱拓扑优化密度云图
由于拓扑优化结果移除对象为非规则形状,考虑到实际加工难度,不可直接使用计算保留结果。对于深色区域需用规则形状进行删除,将拓扑优化结果保存为.stl 格式并导入Geomagic Design X 软件,通过轮廓投影草图编辑获取关键尺寸,如图15 所示,测得质量去除区域存在长为109 mm 的最大矩形。依据尺寸信息使用面片拉伸对原立柱切割获得形状优化模型,如图16 所示。

图15 切割形状及尺寸

图16 立柱形状优化结果
3.2 立柱尺寸优化
对于白色区域和剩余的不规则深色区域,选择前板厚、背板厚、左侧板厚、右侧板厚、底部连接板厚、底部连接板长6 个参数和切割矩形长作为设计对象,进行尺寸调节,考虑到立柱结构由逆向建模获取,尺寸数值存在小数,在SpaceClaim 中使用拉动命令对这7 个设计对象构建参数驱动,圆整化后的设计参数具体数值见表3。

表3 设计参数数值
利用参数相关性,以上述7 个设计参数为对象,将立柱最大总变形、质量、应力和1 阶固有频率作为响应进行灵敏度分析,各参数影响情况如图17所示。

图17 各参数灵敏度
从灵敏度分析结果可知,设计变量X1、X2、X3、X5、X7对优化目标灵敏度较高,X4和X6对立柱质量、1 阶固有频率、等效应力和总变形的影响都非常小。因此,在进行响应面优化时,选择对输出结果影响较大的X1、X2、X3、X5、X7作为设计变量,采用中心复合试验设计(central composite design,CCD),构造出27 个试验设计点,试验设计结果见表4。

表4 CCD 试验设计结果
响应面法本质是利用多项式函数对设计空间内样本进行拟合,建立多变量和响应值之间的逼近数学模型,以便预测非试验点的响应值。本文采用kriging 函数求解响应面拟合度曲线。质量、总变形、1 阶固有频率和等效应力基本在一条直线上,如图18所示,说明CCD 试验所得响应点和响应值较为合理,kriging 函数作为响应面模型符合设计需求。

图18 响应面拟合度曲线
在响应面模型基础上,选用多目标遗传算法(multi-objective genetic algorithm,MOGA),将1阶固有频率、总变形和质量作为目标函数,选取灵敏度分析中影响较大的因素作为设计变量,建立立柱优化数学模型。
式中:y1、y2、y3分别表示为1 阶固有频率、总变形和质量,Xi为设计变量。
将初始样本数设为100,每次迭代数为100,最大迭代20 次,经过7 次迭代后函数趋于收敛,得到频率、质量、应力和总变形优化的3 组候选点,见表5。

表5 优化候选点
对未经过拓扑优化的立柱模型进行尺寸优化。立柱的设计变量中矩形切割长改为顶板厚,具体参数见表6,参数相关性如图19 所示。

表6 设计参数数值

图19 各参数灵敏度
由图19 可以看出,设计变量Z1、Z2、Z5对优化目标灵敏度较高。通过CCD 试验构造15 个设计点,结果见表7。
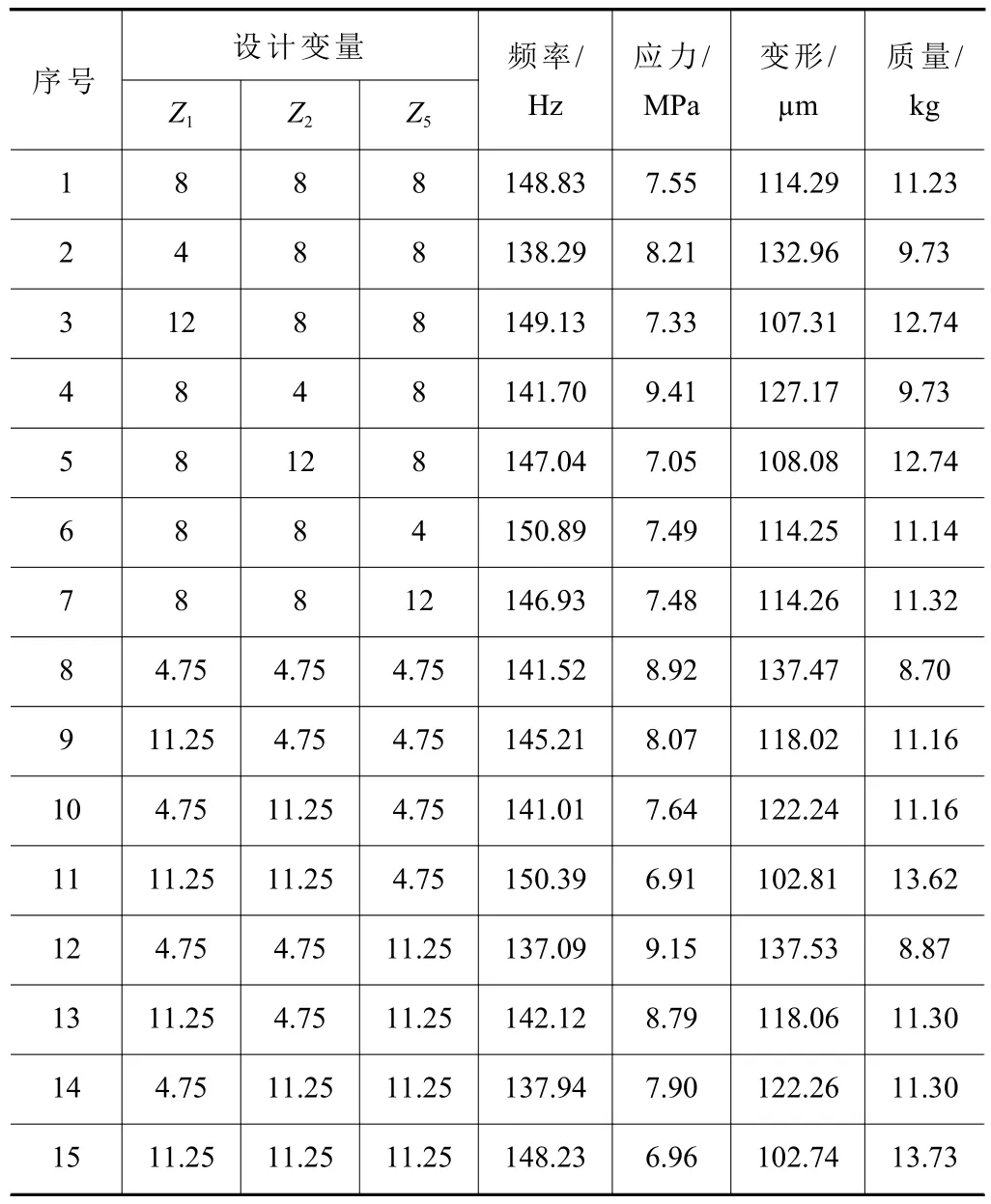
表7 CCD 试验设计结果
响应面拟合函数采用kriging 函数,优化方法选用MOGA,优化数学模型见式(3)和式(4)。计算得到3 组候选点,见表8。

表8 优化候选点
4 立柱优化分析
为尽可能减轻立柱质量,降低产品制造过程中材料消耗,在表5 中选择候选点1、表8 中选择候选点2 参数结果作为模型优化方案。立柱结构优化分析结果见表9。

表9 立柱结构优化分析结果
从表9 可以看出,拓扑优化后的立柱质量减轻12.1%,1 阶固有频率提升19.1%,但总变形增大了5.8%,对钻床使用精度有所影响,不宜作为最终优化结果。在仅进行尺寸优化的情况下,立柱的优化结果变化较小,未达到轻量化的同时提高动态性能的目的。本文最终选用拓扑优化和尺寸优化相结合的方法,1 阶固有频率有效提升16%,质量减轻5.3%,可将优化参数用于生产。使用参数驱动修改模型尺寸并保存为.stl 格式,在熔融型3D 打印机工作下得到1∶0.4 的样品模型,如图20 所示。

图20 立柱优化样品模型
5 结语
针对钻床立柱质量冗余、产品模型数据未知问题,采用三维扫描获取机床整体模型,并使用有限元进行动静态分析,结合形状优化和尺寸优化方法,完成立柱轻量化。
(1)利用三维扫描采集机床结构点云数据,通过逆向建模方法,测得立柱实体轮廓与点云平均偏差为-0.050 9 mm,验证了逆向工程获取机床模型数据的可靠性,并为后续结构优化提供了详细的模型参数。
(2)通过对机床整体静力学分析,发现立柱结构性能是决定机床工作的关键,进一步对立柱仿真分析,结果表明其等效应力远小于材料强度极限,质量存在冗余,1 阶固有模态较低。立柱结构存在较大优化空间。
(3)为获得满足实际需求的立柱结构,在有限元中,使用多目标拓扑结构优化,采用最大规则形状切割原模型,求得1 阶固有频率有效提升19.1%,总变形同时增大5.8%。考虑到变形量增大对机床加工精度影响,进一步优化参数尺寸,最终在变形量基本不变的情况下,立柱1 阶固有频率有效提高16%,质量减轻5.3%。为研究机床零部件动静态特性及优化设计提供参考。
