长江漫滩区软土渗透系数计算方法对比分析

张 杰，黄 勇

（河海大学地球科学与工程学院， 江苏南京 211100）

0 引言

弱透水层是地下水系统中的重要组成部分，主要由黏土、亚黏土及粉质黏土等渗透性较小的土体组成［1］，其渗透系数小于10-5cm/s，比一般含水层小几个数量级。在进行地下水资源评价以及地下水污染预测与防治工作时，确定弱透水层水力参数是至关重要的［2］。在工程建设渗流计算，地面沉降预测、含水层系统水流运移模拟中不可或缺，对于工程的理论计算和分析等具有重要意义。

弱透水层渗透系数的确定方法主要为现场原位试验方法、室内试验法和统计分析法等。弱透水层的渗透系数非常小，抽水试验降深不明显［3］，难以确定。常用钻孔变水头及定水头注水试验法，将弱透水层处理为半无限空间，通过钻孔水位水量变化确定滞后时间，从而确定土层的渗透系数［4］；信亚雯等提出了一种现场确定弱透水层水力参数的钻孔双管试验方法，建立数学模型，并在苏锡常冲积平原验证了该方法的适用性［5］。原位试验在地层原位钻孔进行试验，反映的渗透系数是天然应力状态下的，观测尺度较大，但也存在操作成本高且参数获取的局限性强的问题。

室内试验主要包括渗透仪试验与固结联合渗透实验等［6］。王秀艳等改进研制了渗透时间短的固结联合渗透仪，且能模拟抽水条件下黏性土释水变形过程［7］；林玉祥等构建了基于XGBoost 机器学习算法的模型，对连云港堆场软土静力触探数据进行分析预测，验证了预测模型的精度与准确度［8］。由于试验取土为非原状土，可能由于水理性质变化而产生误差，并不完全具有代表性。对于粗粒介质，前人已给出许多经验公式，例如HAZEN 公式、ALYAMANI-SEN 公式和CARMEN-KOZENY 公式等［9］，而对于黏性土的渗透系数与粒度特征等的定量表达研究较少［10］。张婧玮等引入实际影响黏土渗流的有效孔隙比，修正太沙基渗透系数经验公式，为黏性土渗透系数的估算提供途径［11］。

由于弱透水层位于两含水层间，边界条件比较复杂，难以推导出合适的理论解析表达式。HANTUSH 忽略弱透水层的弹性释水，把越流量假设为在含水层内随坐标变化的垂向补给量，承压含水层不完整井抽水符合THEIS 公式假设条件，上覆潜水含水层通过弱透水层发生越流补给，由此得到容易计算且有足够精度的解［12］。但是由于解析解的假设限制条件较多，往往在实际工程中解析解得出的数值与实际相差过大而导致其的不适用性。随着计算机技术和Feflow 和Aquifer Test 等软件发展［13］，数值模拟可以根据观测水位变化反求含水层水文地质参数，被逐渐广泛运用［14］。石鸿蕾等基于抽水试验与溶质运移试验的多源数据对呼和浩特盆地淤泥层水文地质参数进行反演，与以往研究成果一致性较好［15］。

海太过江通道南岸场地含水层较为简单，为了后续基坑降水提供设计参数，特别是承压含水层可能涉及到的基坑突涌问题，需要确定各含水层和弱透水层的渗透系数，由于确定潜水和承压水渗透系数相对容易，本文以长江软土地区海太过江通道南岸弱透水层为研究对象，采用经验公式法（室内土工颗分试验）、微水试验配线法以及数值模拟反演法，对弱透水层的渗透系数进行计算，并对计算结果进行讨论分析，得到比较适用于弱透水层渗透系数的计算方法。

1 场地地质及水文地质条件

海太过江通道南岸场地区位于长江三角洲冲积平原区，地势平坦开阔，地形地貌简单。场地内第四系较厚，主要由黏土、粉质黏土与砂层组成，按照地下水埋藏条件可分为潜水与承压水两层。潜水含水层主要为填土、粉土与粉砂，厚度约为10m，潜水位埋深浅、起伏小，主要接受大气降水和侧向径流补给，以蒸发和侧向径流为主要排泄方式，潜水与地表水（长江、水渠及鱼塘）呈互相补给关系；承压含水层主要由粉砂、粉细砂、含砾中粗砂构成，厚度约为60m，接受长江上游的侧向地下径流补给、垂向含水组间的越流补给及黏性土的释水补给，以地下径流及人工抽吸为主要排泄方式，富水性好；中部的弱透水层主要为淤泥质土与粉质黏土，构成相对隔水层，厚度约为40m（图1）。

图1 研究区场地地层及含水层概化Figure 1 Overview of Stratigraphy and Aquifer in the Study Area

2 弱透水层渗透系数计算

2.1 室内试验法

张婧玮等在太沙基渗透系数经验公式的基础上，引入实际影响黏土渗流的有效孔隙比eu，采用拟合法得出黏粒含量P与eu的定量关系，利用常规土壤参数，对太沙基渗透系数经验公式进行修正，从而完成了对黏性土渗透系数的预测，并验证了太沙基修正公式在平原区的适用性［11］。太沙基渗透系数经验公式：

式中：K为渗透系数，cm/s；e为孔隙比；d10为土样颗粒的有效粒径，mm。

引入黏性土有效孔隙比eu，对太沙基经验公式进行修正，式（1）可以改写为

通过在江汉平原采集的土样根据室内渗透实验方法获得的黏性土渗透系数与土壤的颗分曲线级配特征等参数，利用数学拟合法得出黏粒含量P与有效孔隙比eu的显著二项式拟合关系，得到：

式中：P为土样黏粒含量，%。

2022年2月通过对海太过江通道南岸试验区现场采集目标层土样并进行室内颗粒分析试验，得出土体的颗粒级配曲线、黏粒含量P，以及有效粒径d10，根据式（3）可以得到弱透水层的渗透系数（表1）。

表1 基于修正的太沙基经验公式计算结果Table 1 Calculation results based on modified Terzaghi empirical formula

由表1 可知，弱透水层渗透系数平均值为7.196×10-5cm/s，标准差为4.565×10-5。

由式（2）可知，渗透系数与孔隙率成正比，随粒径二次方的增加而增加。通过对目标地层土体的室内样品粒度颗粒分析，采用修正后的太沙基渗透系数经验公式计算渗透系数，仅用到黏粒含量P，以及有效粒径d10的土壤参数，在实际工程中获取较为简单。根据现场孔压静力触探CPTU 原位测试技术所得目标层渗透系数为6.524×10-5cm/s，与本文计算结果基本一致，因此，修正的太沙基经验公式可用于弱透水层渗透系数的计算，具有较好的适用性。

2.2 微水试验

微水试验作为一种现场测定含水层渗透系数的新型试验技术，具有简便快速、设备简单、经济成本低等特点，在近年来得到较多应用［16-17］。该方法通过井孔内水位的瞬时变化，记录钻孔水位随时间的变化，从而通过配线法计算渗透系数。KIPP 模型适用于承压水与潜水含水层，柱坐标系下的水流运动方程：

式中：h为含水层水头，m；t为时间，s，注水或取水瞬时为起始时间；S为贮水系数；T为导水系数，m2/s；r为柱坐标原点的径向距离，m。

KIPP 引入无量纲的参变量，将上述方程转换无量纲形式，得到一系列无量纲水位变化W和无量纲时间t的标准曲线。据微水试验得到的钻孔水位变化W与时间t的对应观测资料，在与标准曲线相同模数的半对数纸上，时间取对数绘制试孔水位变化与时间的关系曲线（实测曲线）；通过平移坐标轴来匹配实测曲线与标准曲线；记录拟合标准曲线的ζ、α值；任选一个匹配点，记录匹配点在标准曲线上的坐标t值和W'值，同时在实测曲线上记录匹配点的时间值t和水位变化值W［18］。最终，导水系数T和渗透系数K分别为

2022年8月在海太过江通道南岸共布置了两个试验孔（表2）。现场试验中，向试验孔中注满水，并观测孔内的变化。观测时间约8h，其中试验孔SBRT-1 的初始水位埋深为544cm，250min 恢复到初始水位；试验孔S-BRT-2 的初始水位埋深为621cm，450min 恢复到初始水位。将水位恢复曲线代入KIPP 模型进行微水试验配线（图2）。相对于试验孔S-BRT-1，试验孔S-BRT-2水位下降较慢。

表2 微水试验计算结果Table 2 Calculation results of slug test

图2 KIPP 模型微水试验配线Figure 2 Slug test of KIPP model

经过计算得出，渗透系数平均值为1.495 9×10-5cm/s（表2）。结合试验数据与结果分析，发现微水试验所得到的弱透水层参数比经验公式结果偏小，但数量级相近。微水试验对弱透水层的影响仅限于孔周围小范围土体，因此微水试验计算所得结果反映的是弱透水层在一点上的参数性质，通过多点的微水试验，可以获取整个研究区的渗透系数，具有较强的适用性。

2.3 数值模拟反演法

由于解析解的假设限制条件较多，实际工程中可用数值模拟反演法对场地水文地质参数进行求解［19-20］。采用FEFLOW 软件对研究区进行地质建模，并通过数值反演获取弱透水层的渗透系数。根据前述的研究区抽水试验场地水文地质条件，对整体含水层结构进行概化如下：其中潜水含水层厚度约10m，相对隔水层厚度约40m，承压含水层约60m，对承压含水层进行抽水试验。由于试验场地的地势平坦，研究区域的岩性和地质条件变化程度比较小，岩性较为均匀且抽水井相距较近，影响范围较小，故对研究区地层岩性参数在水平方向上不做分区，并在模型平面内连续分布。故将其概化为均质、各项异性介质，模型概化为三维承压含水层非稳定流模拟问题。

试验场地承压含水层布置见图3，其中抽水孔为NC-C1 和NC-C2，观测孔为NC-G1 和NC-G2，观测孔和抽水孔相距10m。弱透水层观测孔编号为NRT，与NC-C1 相距约28m。模拟区域为抽水影响范围，侧向边界为定水头边界，模型底部为隔水边界。图4为研究区含水层三维地质数值模型与含水层网格剖分图，采用三角形网格剖分，共20 176 个节点，29 679个单元。

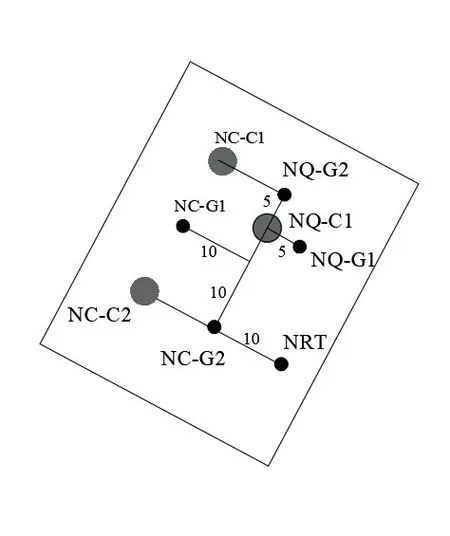
图3 南岸抽水试验孔布置Figure 3 Layout of pumping test holes on the south bank

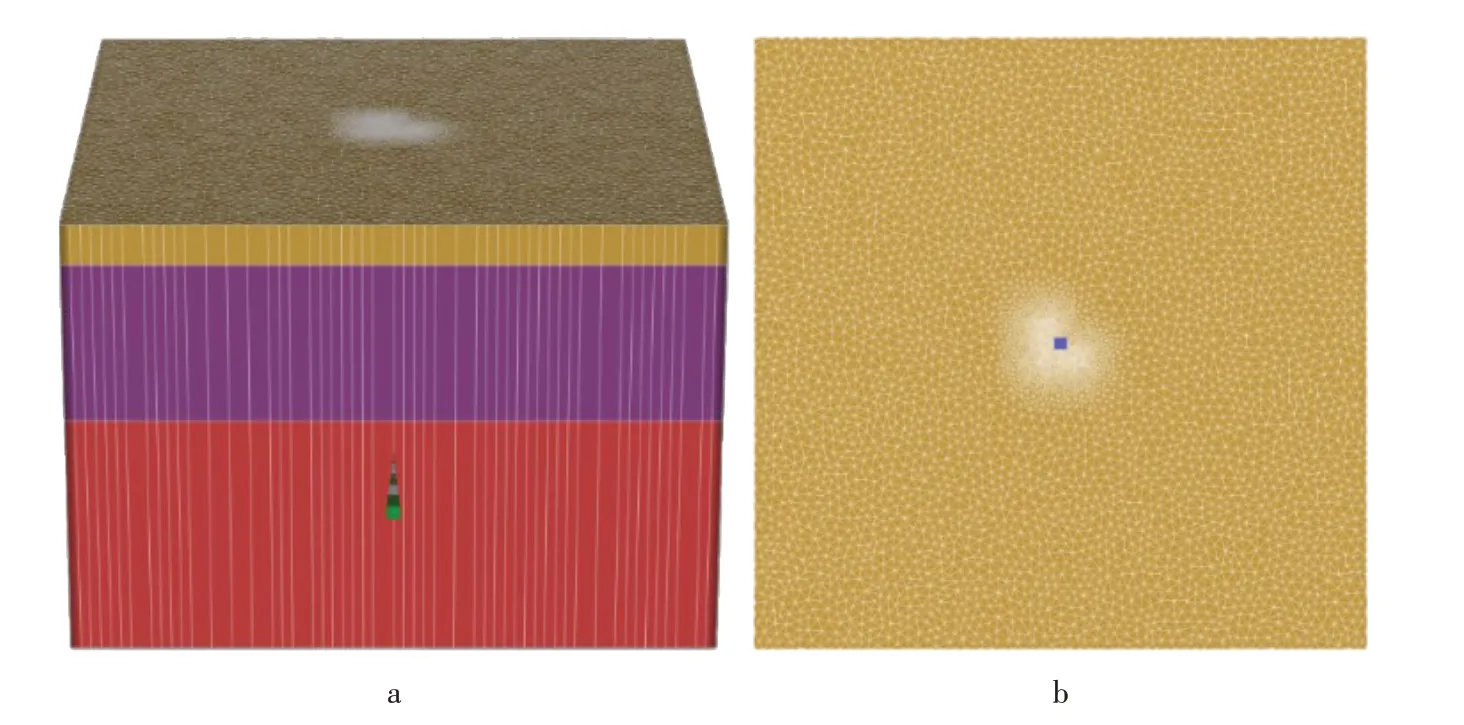
图4 研究区含水层三维地质模型（a）和含水层网格剖分（b）Figure 4 3D geological model of aquifer in the study area（a）and aquifer mesh generation（b）

试验场地一共进行了3 个落程的单井抽水试验。3 个落程的承压含水层最大降深分别为2.275、7.16、12.665m，弱透水层降深较小，且有一定的滞后效应。根据试验场地3 次单井抽水试验与1 次群井抽水试验数据，对研究区弱透水层与承压含水层进行数值反演。依据室内试验所得参数作为初始值，通过抽水试验中各井水位观测值与模型水位计算值的差值对各含水层参数进行调整，从而得到最佳的拟合效果（图5）。

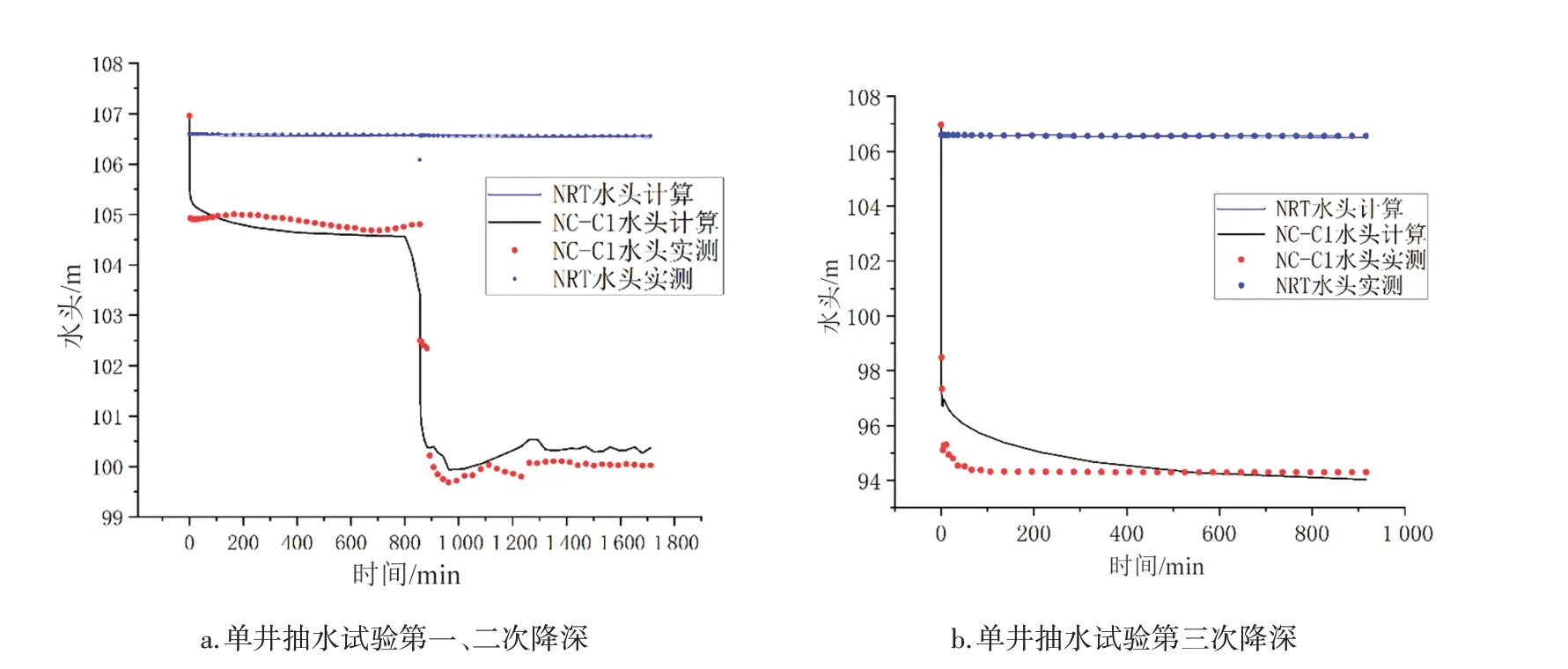
图5 试验场地单井抽水试验实测水位和模拟水位拟合Figure 5 Fitting of measured and simulated water level in single well pumping test at test site

由图5可知，在抽水的前期，承压含水层的水位下降速度较快，而由于弱透水层的渗透系数远小于其他含水层，所以出现了比较明显的滞后现象。随着抽水时间的延长，弱透水层水位缓慢下降。从图5 中可以看出实测水位与模拟计算水位值差值较小，拟合较好，表明了反演所得的水文地质参数较为合理，试验场地各含水层参数反演结果见表3。

表3 各试验含水层水文地质参数反演结果Table 3 Inversion results of hydrogeological parameters of each experimental aquifer

3 弱透水层渗透系数结果对比分析

本文采用（室内土工颗分试验）经验公式法、微水试验配线法以及数值模拟反演法，对于海太地区弱透水层的渗透系数进行求解，计算结果见表4。

表4 各方法参数结果汇总Table 4 Summary of parameter results for each method

以上各类方法对比看出，微水试验比抽水试验数值反演所得参数偏小，但结果平均值在同一数量级，室内颗分试验结果经经验公式计算后，与现场试验所得结果也相近。由此可见，几类方法均可用于弱透水层的渗透系数计算，且能保证一定的精度与合理性。在实际工程中，由于大部分情况与理想假设存在差距，前期勘探未查明的区域，边界条件的复杂性、含水介质的非均质性与各向异性，含水层地板的起伏，试验抽水的不稳定等各种因素影响，均会限制单一实验结果的准确性与适用性。为避免单一方法导致的求参偏离，采用室内、现场试验与数值模拟反演等方法相互验证，减少了单一试验方法影响范围小、取样偶然性等对结果的影响。根据工程实践中的最不利原则，研究区弱透水层渗透系数建议取值为8.10×10-5cm/s。

4 结论

针对海太过江通道南岸地区的弱透水层渗透系数，采用经验公式法（室内土工颗分试验）、微水试验配线法以及数值模拟反演法进行计算，各方法均可适用于弱透水层渗透系数的计算，也具有一定的局限性，按照工程最不利原则，渗透系数通常取较大值。在实际工程实践中，由于弱透水层渗透系数偏小、取样与各类试验的范围较小、单一试验具有局限性，得到的结果可能出现偶然性。且粉质黏土中可能存在的薄层粉细砂、粉土夹层和透镜体，渗透系数离散性较大，而采用多种室内、现场试验与计算机数值模拟方法对海太地区南岸弱透水层渗透系数进行计算，相互验证得到的最终结果往往对工程实践具有更强的指导性。