熵权法改进的模糊数学滑坡稳定性评价方法研究

霍善欣，王新刚，薛 晨，王友林，李 琦，刘 凯

（1.大陆动力学国家重点实验室（西北大学地质学系），陕西 西安 710069；2.陕西省水工环地质调查中心，陕西 西安 710068）

0 引言

中国构造与地震活动强烈，地形地貌、地质条件复杂，加上气候类型多样，人类工程活动剧烈，地质灾害易发、频发[1]，其中，滑坡是发生次数最高、最为常见的一种地质灾害类型。滑坡通常会对人们的生命财产和基础设施建设造成巨大的伤害与损伤[2]，而滑坡的稳定性评价可以为滑坡的防治提供重要的依据，从而最大程度降低因灾伤亡和经济损失[3]。

目前滑坡稳定性评价方法主要分为定性和定量两种方法，定性方法有自然历史方法、工程类比方法[4]、专家系统方法[5]等，定量方法包括传统的稳定系数法[6]、突变理论模型[7]、神经网络模型[8]、灰色关联分析模型[9-10]和模糊综合评价模型[11]等。滑坡的发生存在多种因素影响，各因素之间的影响与条件具有较为模糊的概念，不具有清晰、明确的关系，使用模糊数学方法进行评价可以较好地解决这一类问题。模糊综合评价方法具有模型简单、多层次、定量化和易掌握的特点[12]，但是该方法单一评价结果的准确性并不十分明确。

为了能够更好地对滑坡稳定性做出准确、合理的评价，本文在采用模糊综合评价法的基础上，引入“熵”的概念，利用“熵值”获取修整后的权重系数，提高评价结果的客观性、准确性。在系统分析陕西省勉县新铺镇杜家山滑坡地质条件基础上，先通过熵权法[13]求出评价因子权重，再由模糊数学法建立相应的隶属函数，并进行综合评价，得出该滑坡稳定性系数，最终使用数值模拟软件GeoStudio 对滑坡进行稳定性分析计算，验证了改进后的模糊综合评价方法。

1 滑坡概况

杜家山滑坡位于勉县新铺镇杜家山村，新铺镇位于“勉略宁”地质金三角，该区域地质环境条件复杂，被地质学家李四光誉为亚洲的“乌拉尔”。根据野外调查，滑坡滑体为碎石土，为一浅层堆积层滑坡。受人类活动影响，坡面呈阶梯状（图1），该处坡高约70 m，平均坡度31°，坡形为多级台坎状，地形东北高西南低。坡顶为一处通村公路，坡脚为陡立临空面，临空面高约15 m。2021 年8 月21 日勉县突发特大暴雨，坡体在自重及降雨作用下发生滑动，在滑坡体后缘及滑坡周界形成多条拉张裂缝，侧壁、错台等滑坡特征明显（图1）。滑坡长约175 m，宽70 m，滑体厚3.5 m，滑向225°，体积4.29×104m3，平面形态为舌形，剖面形态为直线形。

图1 杜家山滑坡Fig.1 Dujiashan landslide

经实地勘察，该滑坡坡体地层主要分为四层（图2）。表层为厚约0.3 m 的耕土层。上部主要为碎石土，呈黄褐色，稍干，较密，含少量岩石碎屑。中部为千枚岩，下部为板岩。根据地表出露和钻探揭露，该滑坡滑体主要由第四系中下更新统冲洪积层组成，厚度较小，约为3.5 m，主要为棕黄色、黄色粉质黏土，土层中夹杂大量砾石，约32%，土体整体较湿，其孔隙比为0.527～0.608，含水率为16.5%～18.1%。

图2 杜家山滑坡剖面图Fig.2 Profile of Dujiashan landslide

2 基于熵权法改进的模糊综合评价法的滑坡稳定性分析

2.1 基于熵权法的模糊综合评价

模糊综合评价方法，是一个基于模糊数学方法的综合评价方法，在实现模糊综合评价的过程中，怎样设定评价因素的权重是一个问题。评价因子的权重取值方法一般有专家经验分析法、层次分析法[14]和熵权法。专家经验分析法与层次分析法，利用数据定性因素成分较大，主观意识比较强，也导致说服力小。为降低主观意识的影响，本文引入熵权法来确定该滑坡各评价因子的权重。1865 年，德国的物理学家克劳修斯首次提出了“熵”的概念，其最初仅是一个简单的物理学变量参数，后其本质才逐渐被解释清楚，即用来解释一个系统“内在的混乱程度”。基于熵的本质特性，可以采用熵值判断某个评价因子的离散程度：评价因子的离散程度越大，对滑坡稳定性的影响也就越小，则权重越小，反之权重越大[15]。鉴于熵权法确定评价因子权重的客观性与深刻区别因子的能力，本文考虑引入“熵”值，对模糊综合评价进行改进。

2.2 计算步骤

首先根据杜家山滑坡的实际勘察数据，建立该滑坡的因素集U={u1,u2,u3,···,un} 和评价集V={v1,v2,v3,···,vm}，其中ui、vj分别为该滑坡稳定性的评价因子和评价等级，即该滑坡可能出现的分级结果。然后利用熵权法，通过各评价因子标准化后的数值分别确定各个因子的权重；接着构建隶属函数，分别计算出它们的隶属度向量，进而得到评价矩阵；最后将权向量与评价矩阵进行模糊运算，得到模糊综合评价结果。

2.2.1 确定滑坡稳定性的因素集和评价集

本文通过前期的野外调查资料及DEM（数字高程数据），统计得出影响杜家山滑坡稳定性的主要因素，并根据堆积层滑坡的特征，建立该滑坡的因素集：

式中：u1——坡度/（°）；

u2——斜坡结构；

u3——堆积层厚度/m；

u4——切坡高度/m；

u5——风化程度；

u6——距水系距离/m；

u7——坡体高差/m；

u8——距道路距离/m；

u9——坡型。

其中斜坡结构、堆积层厚度、切坡高度、风化程度、坡型为野外调查所得，其他因子通过DEM 获取。堆积层厚度由野外钻探、物探和探槽等多方法综合得出。

根据《滑坡防治工程勘察规范》[16]（GBT 32864—2016）第13.3.4 条的规定，将滑坡的稳定状态分为四级，分别为稳定、基本稳定、欠稳定和不稳定。由此，设评价集为

式中，v1——稳定；

v2——基本稳定；

v3——欠稳定；

v4——不稳定。

2.2.2 计算评价因子的权重

2.2.2.1 构建样本矩阵

假设有n个样本，m个评价指标，则有样本矩阵P=[Pij]nm：

式中：Pij——第i个滑坡的第j个评价因子的实际参数；i=1,2,···，n；j=1,2,···,m。

2.2.2.2 对不同的评价因子进行标准化处理

要去除不同评价因子的量纲差别，须对样本数据实行标准化变换处理，即所谓min-max 标准化。min-max的标准化方法是对原始数据进行线性变换后，当数值为正指标（实际值越大表现就越好的指标）时，有：

当数据为负指标（实际值越小表现就越好的指标）时，有：

式中：X——标准化的值。

通过原始数据的标准化，得到标准化矩阵B：

由于min-max 标准化处理需要多组数据结合，因此本文选取了调查区内较为典型的九处滑坡（区内其他典型堆积层滑坡）作为数据组（表1）。在选取的9 个评价因子当中，距水系距离与距道路距离表现为负指标，其值越大，则滑坡稳定性受其影响越小，坡体越稳定，采取式（5）进行负指标标准化；其他7 个评价因子进行正指标标准化，采用式（4）。得到标准化矩阵式（7）。评价体系见表2。

表1 新铺镇地区滑坡稳定性评价指标数据Table 1 Data of landslide stability evaluation indicators in Xinpu Town area

表2 滑坡稳定性评价指标体系及分级标准Table 2 Indicator system and grading standards for landslide stability evaluation

2.2.2.3 评价因子的熵值和权重计算

根据熵值的定义，计算出各个评价因子的熵值E，进而得出各因子的权重，即有：

式中：Ej——熵值；

N——常数，取值为1/ln(n)；

fij——相对比重，i=1,2,···n，j=1,2,···,m。

最终得出熵权矩阵：

2.2.3 各评价因子隶属度的计算及模糊矩阵的建立

2.2.3.1 构造评价因子的隶属函数

按数学分类方法分类，涉及的指标有离散型（定性指标）和连续型（定量指标）[17]。连续型评价因子中对于水系距离与道路距离两个因子采取偏小型隶属函数，对于坡度、坡高差、切坡高度和风化程度4 个因子采取偏大型隶属函数，对于离散型的评价因子采取正态分布型隶属函数。

式中：rij——第i个评价因子对第j个评价的隶属度；

x——评价因子的值；

a，b——代表对应稳定性等级的评价因子的上下界。

代入杜家山滑坡，通过式（12）—（16），计算得出滑坡的模糊关系矩阵，即

将权矩阵A与评价矩阵R进行模糊矩阵运算，计算得出杜家山滑坡稳定性评价隶属度：

杜家山滑坡对稳定、基本稳定、欠稳定和不稳定四种状态的隶属度分别为0.885，0.556，0.475，0.038，根据最大模糊隶属度原则，得出杜家山滑坡处于稳定状态。

3 GeoStudio 有限元数值模拟分析

上述基于熵权法改进的模糊数学综合评价方法考虑了坡度、斜坡结构、堆积层厚度、切坡高度、风化程度、距水系距离、坡体高差、距道路距离和坡型等9个因子对滑坡稳定性的影响。对于堆积层滑坡，降雨是影响坡体稳定性的重要因素之一。在镇域范围内降雨量变化较小，新铺镇内滑坡所受降雨量基本一致，因此在上述评价方法的基础上需考虑降雨对于特定滑坡的影响，并作为评价结果的重要补充。在此背景下，以新铺镇杜家山滑坡为例，使用GeoStudio 数值模拟软件，对杜家山滑坡在未降雨与降雨2.4 h、4.8 h、7.2 h、9.6 h、12 h、14.4 h、16.8 h、19.2 h、21.6 h 和24 h 10 种时长条件，分析不同降雨时长下坡体变形和孔隙水压力变化情况，计算分析各工况下坡体稳定性的变化情况。

3.1 数值模型的建立

根据野外勘察获得的资料，确定杜家山滑坡的地质剖面。采用AutoCAD 软件进行构建模型前的处理，概化该滑坡的地质模型，模型高为70 m，最低高程600 m，最高高程670 m，模型底部长度为163 m，具体几何模型如图3 所示，模型中共有三种岩土材料，分别为碎石土、千枚岩以及板岩，输入的材料相关参数为室内土工试验所获得的数据。在对该滑坡地质模型进行单元划分时，考虑到模型精度和计算收敛的难易程度，采用四边形单元进行单元划分，模型最小尺寸控制在0.5 m，同时获得降雨过程中坡体变形、孔隙水压力、应力及应变等特征的发展和变化过程。

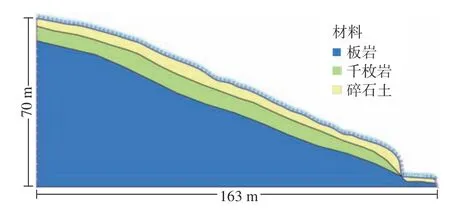
图3 杜家山滑坡数值模型Fig.3 Numerical model of Dujiashan landslide

3.2 降雨条件下滑坡变形规律

降雨过程中各时刻坡体位移云图如图4（a）—（k）所示，在降雨过程中随着水分入渗土体，土体自重增加，抗剪强度减小，因此下滑力增大而抗滑力减小。可以看出坡体将在坡体中部最先产生破坏，其次为坡脚临空面处。未降雨条件下，坡体未产生变形。在经历勉县“8•21”特大暴雨之后，杜家山滑坡的坡体受到大气降水入渗的影响，不仅使滑坡体的重度增加，而且也削弱了滑坡堆积层与基岩接触面的抗滑能力，使得上部堆积层受到自重和水压力的双重作用，从而发生蠕滑，并从滑坡前缘挤压剪出。随着降雨的持续大量地下水在堆积层下部基岩顶面汇集并形成附加渗透压力，加快了软弱结构面裂隙的扩展和滑动面的贯通，最终使上覆土体沿软弱结构面产生整体滑动，形成蠕滑-推移式破坏。随着降雨的进行，坡体开始产生相应的变形，当降雨时长为2.4 h时，坡体最大变形量为0.644 m，见图4（b）；在24 小时降雨条件下，滑坡滑动的最大位移为6.5 m，见图4（j），最大的变形区域位于坡体的中部碎石土地层。

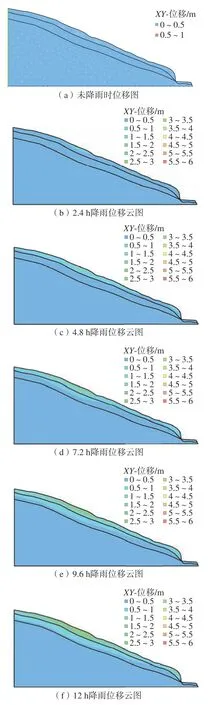
图4 不同降雨时长下位移云图Fig.4 Displacement clouds map for different rainfall durations

3.3 降雨条件下滑坡孔隙水压力变化规律

不同降雨时长下坡体孔隙水压力分布云图如图5（a）—（j）所示，在整个降雨过程中，降雨前期坡体浅层碎石土含水率低，雨水的入渗速度最大，上部碎石土的渗透系数相对千枚岩和板岩较大，雨水在碎石土中入渗较快。随着降雨时长的不断增大，雨水逐渐由碎石土渗入千枚岩地层进而入渗到板岩地层，饱和区的面积不断扩大，同一位置的孔隙水压力随着降雨时长的增加而不断增大。坡脚处由于雨水汇集土体孔隙水压力明显增加，当降雨时长为2.4 h 时，坡体内部最大孔隙水压力为0.15 kPa，见图5（a）；当降雨时长为24 h 时，坡体内部最大孔隙水压力为33.03 kPa，见图5（j），由此可见随着降雨时间的增加坡体内部最大孔隙水压力增大，且饱和区的面积不断增大。

图5 不同降雨时长下孔隙水压力内部云图Fig.5 Internal contour of pore water pressure under different rainfall durations

3.4 降雨条件下滑坡稳定性系数变化规律

利用GeoStudio 软件slope 模块采用Morgenstern-Price 方法分析杜家山滑坡稳定性，不同降雨时长下滑坡稳定性系数变化如图6 所示，在未降雨条件下稳定性系数为1.243；降雨2.4 h 后滑坡的稳定性系数大幅度减小，降为1.059；降雨9.6 h 后滑坡的稳定性系数降为0.997，此时坡体失稳。由图6 可知，降雨前7.2 h 杜家山滑坡稳定性系数下降较快，在降雨7.2 h 后稳定性系数下降变慢，这是7.2 h 后滑坡内部的滑动面已经整体贯通，此时滑坡已经失稳，稳定性系数将基本不再变化。

图6 杜家山滑坡稳定性系数随降雨时长变化Fig.6 Validation of stability coefficient of Dujiashan landslide changes with rainfall duration

通过数值模拟法进行滑坡稳定性定量化分析验证，同种工况下改进后的模糊数学评价结果与数值模拟计算结果相吻合，如改进后的模糊综合评价通过矩阵计算及隶属度最大原则得出杜家山滑坡在天然工况下属稳定状态，数值模拟法得出杜家山滑坡在未降雨条件下稳定性系数为1.243（图6），属稳定状态，说明了所提出的新方法具有一定的可靠性。考虑滑坡不同降雨时长下稳定状态时，利用试验获取力学参数进行数值模拟的稳定性分析方法，相比于熵权法改进后的模糊数学综合评价方法更加精确，且能够反映滑坡的位移、孔隙水压力和稳定性系数等变化情况。而基于熵权法改进的模糊数学滑坡稳定性评价方法较为快速简捷，相比数值模拟方法较大的减少了稳定性评价所需的工作量和试验成本，可用于临灾快速预警、应急救援等突发情况下的滑坡防灾减灾工作。

4 结论

本文将熵值求取权重的方法与模糊数学综合评价法相结合，建立应用于秦巴山区勉县新铺镇的堆积层滑坡稳定性综合评价方法，得到了以下结论：

（1）本文全面地考虑了影响滑坡发生的主客观因素及堆积层滑坡特征，建立了基于熵权法改进的滑坡稳定性评价的指标体系，并考虑了坡度、斜坡结构、堆积层厚度、切坡高度、风化程度、距水系距离、坡体高差、距道路距离及坡型等指标。

（2）新提出的基于熵权法改进的模糊数学滑坡稳定性评价方法克服了传统模糊综合评价方法主观性判断滑坡影响因子权重的弊端，新方法能够深刻反映因子区分，与原本的模糊综合评价相比可以客观地确定评价因子的权重，且算法简捷，快速。

（3）改进后的模糊数学评价结果与数值模拟计算结果相同，两种方法评价结论较为吻合，相比之下，数值模拟评价方法可计算的工况更多，更能反映滑坡滑动的动态变化，补充了新方法对于动态条件下无法分析的不足。但本文所提出的新方法减少了数值模拟稳定性评价所需的工作量和试验成本，可用于临灾快速预警、应急救援等突发情况下的滑坡防灾减灾工作。

（4）本文提出的基于熵权法改进的模糊数学综合评价方法还具有一定的局限性，对于条件变化的动态条件（如降雨）下稳定性不能评价等，更适合现状条件下的滑坡稳定性评价，在后续的调查研究中对该方法进行完善，使其能够更好地用于多种工况下的滑坡稳定性评价。