线性系统理论仿真实验平台的设计与应用

易 坚,吴夏来,杜树新

(湖州师范学院 工学院,浙江 湖州 313000)

0 引 言

《线性系统理论》是控制理论领域非常重要的一门研究生专业基础课程,其对学生在控制工程领域的学习和研究具有重要作用,且在实际生活中应用广泛[1].《线性系统理论》主要研究线性动态系统的数学理论和方法,包括线性时不变系统、线性时变系统、离散时间系统等.《线性系统理论》课程的作用主要是帮助学生深入理解线性系统的基本概念、性质和特征,培养学生分析和设计复杂系统的能力,提高学生的数学素养,从而为进一步研究和应用打下基础[2].目前,线性系统理论课程教学存在以下问题：①课本内容对数学知识要求高,且计算量大[3];②学生来自不同的院校,数学基础差异大[4];③来自不同本科专业的学生具有不同的专业背景;④课本中的相关理论没有对应的结果仿真图,课程内容抽象且不易理解.基于此,不少高校教师对该课程的教学进行了改革.目前,已知的教学改革手段主要有：课程内容优化[5],构建系统化知识体系;教学案例建设;丰富教学手段,如课堂研讨、 混合教学[8]等.然而,这些教学改革手段并没有很好地解决课程理论概念抽象不易理解且数学计算要求高等问题.虽然通过Matlab软件编程可对课程内容进行仿真和计算,降低学习难度,但Matlab语言编程对不少基础较差的专业硕士研究生来说,其难度较大且耗时,不易实施.

针对线性系统理论课程存在的问题,设计一个直观易操作且无需编程的线性系统理论仿真实验平台,对线性系统理论的学习和教学来说是非常有必要的.本文利用Matlab开发一个线性系统理论仿真实验平台,其包含与课程主要知识点对应的7个仿真实验和1个以桥式吊车为被控对象的综合仿真实例.当使用仿真实验平台时,只需输入线性系统的相关参数,就可得到相应的理论分析结果和仿真结果图.借助本仿真实验平台可避免复杂的数学计算,并可通过仿真结果图直观地理解线性系统理论知识,这对激发学生的学习兴趣和辅助任课教师高效教学都有很大帮助.通过本仿真实验平台的使用,也可提高学生对线性系统理论知识的综合应用能力,帮助他们更好地应对实际工程问题.

1 线性系统理论仿真实验平台的设计

为降低线性系统理论学习的难度,本文设计一个仿真实验平台.该仿真平台操作简单、计算结果准确,使用者能快速得到仿真结果,方便学习、实验和验证.该平台运行要求低,具有高移植性,能实现线性系统理论中的多种功能.

1.1 课程内容与仿真实验平台

针对线性系统理论的重要知识点,本仿真实验平台设计7个线性系统理论基础知识的仿真实验,其包括：①线性系统的运动分析.以状态空间描述为对象,研究因不同输入作用和初始状态的激励所引起的状态变化或输出响应.该内容的仿真可用step()函数得到系统的阶跃响应结果图,用impluse()函数得到系统的脉冲响应结果图[9].②矩阵指数函数(eAt)的求解.这是一种将方阵映射到另一个方阵的函数,是线性系统运动分析计算过程中的核心步骤.该内容可用laplace()函数实现快速计算.③系统的稳定性判定.判断系统在运行过程中是否具有良好的稳定性和鲁棒性,是研究动态系统的重要工具.该内容可用lyap()函数实现李亚普诺夫第二法对系统稳定性的判断.④系统能控、能观性判定.评估系统是否可以被控制和被观测,是控制系统设计和分析中的重要概念.该内容的仿真可用ctrb()函数得出能控性判别矩阵,用obsv()函数得出能观性判别矩阵,从而判断系统的能控和能观性.⑤系统极点的配置.通过状态反馈将系统的极点或特征根配置在期望的位置上,以达到所需的控制性能和稳定性要求.该内容的仿真可用place()函数实现极点配置的状态反馈矩阵,用step()函数得出系统通过状态反馈配置极点后的阶跃响应结果图.⑥带观测器的闭环系统.用于估计系统的未知状态变量,以提供对系统状态的反馈信息,从而实现对系统的控制.该内容的仿真可用acker()函数实现极点配置的观测器增益矩阵,用step()函数得出系统通过观测器配置极点后的阶跃响应结果图.⑦解耦控制.旨在减弱或消除多变量系统中的耦合影响,使系统的各个输出变量能够独立地被控制.该内容的仿真可用inv()函数、place()函数实现,从而获得系统解耦控制中的预变换矩阵、预状态反馈矩阵,以及解耦控制后系统状态空间方程的矩阵系数.

上述的线性系统理论知识点,虽然可利用Matlab中的m语言函数实现,但对编程基础差的学生来说,其编程耗时多且仍然存在困难.本文开发一个无需编程的线性系统仿真实验平台,其非常有利于学生的学习.为通过综合利用线性理论知识来实现线性系统的控制设计,本仿真实验平台还开发了1个以桥式吊车为对象的控制设计仿真实例.仿真实验平台的首页目录见图1.

1.2 仿真实验平台的操作流程

为提高仿真实验平台使用的便利性,本仿真实验平台的操作流程设计见图2.以控制系统极点配置的仿真为例,在进入该仿真界面后,只需输入系统的参数和所需配置的极点,点击“极点配置后”按钮,即可显示实现极点配置的状态反馈矩阵(K),并给出系统极点配置后的阶跃响应结果,见图3.此外,在该仿真界面上还可点击“极点配置前”按钮,查看极点配置前的系统阶跃响应结果,以观察极点配置的作用.在仿真结束后,可点击“返回目录”按钮,到目录界面选择其他仿真.本仿真实验平台界面简洁、操作简便、仿真结果直观,对线性系统理论的学习很有帮助.

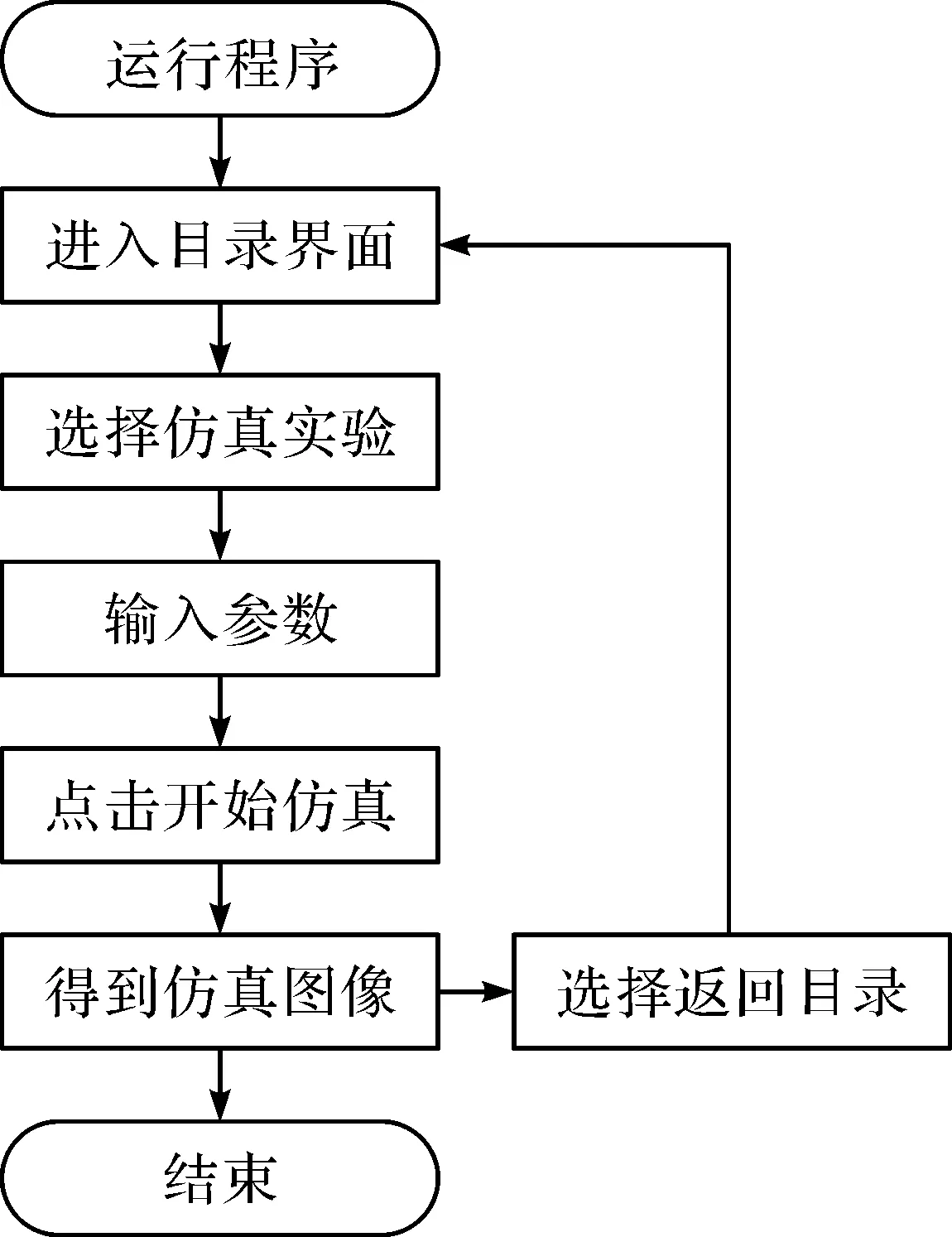
图2 仿真实验平台操作流程

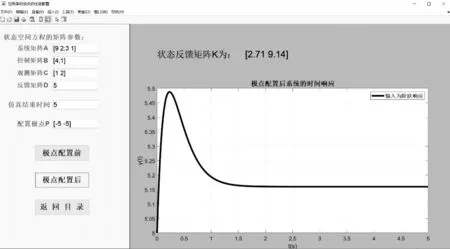
图3 系统的极点配置

1.3 仿真实验平台的运行环境

仿真实验平台是基于MatlabR2021b开发的,在安装MatlabR2021或其他最新Matlab版本的电脑上都可运行,能成功地降低本仿真实验平台的运行环境要求,提高可移植性.仿真实验平台的运行环境有以下要求：

(1)硬件要求：CPU为2.5 GHZ及以上;内存为4 G及以上.

(2)软件要求：windows10-64位操作系统;运行环境为MatlabR2021b及以上版本.

2 综合应用实例

线性系统理论基于状态空间描述进行线性系统的定量和定性分析,进而实现系统的综合设计.线性系统综合设计是线性系统理论的综合应用,能充分提高学生对线性系统理论的理解深度和应用能力.本仿真平台设计1个桥式吊车控制系统设计实例,以帮助学生通过对桥式吊车的系统建模、性能分析和跟踪控制设计,进一步掌握系统理论知识,提高解决工程实际问题的能力.

2.1 桥式吊车的控制系统

桥式吊车是一种大型的用于装卸、搬运的工具,普遍用于码头、车站、仓库和现代化工厂等[10-11].它也是控制工程领域的一个热门研究方向[12].桥式吊车的运动系统包括：桥架驱动系统、小车驱动系统和重物吊装系统[13].桥式吊车的工作流程通常包括3个步骤：将重物从地面吊起到指定高度;通过桥架和小车的驱动系统将其移动到特定位置上方;将重物放置到指定位置.重物吊装系统采用柔性物品如绳索进行吊装,使得吊装工作相对轻松、便利.然而,这种吊装方式也存在一个主要缺点,即当吊车行驶时,会使重物产生不可控的摆动[14],这不仅严重影响吊车准确定位和装卸重物的精度,还会对吊车装卸和搬运过程的安全性造成影响.解决这个问题的关键在于设计合理的控制规律或调节手段,以减少或避免重物的摆动,确保准确的定位和卸载,从而提高吊车的工作效率[15].

2.2 桥式吊车的数学模型

桥式吊车系统主体包括小车、重物、绳索、电机等,在忽略空气阻力和各种摩擦力后,桥式吊车系统可抽象为小车和重物组成的系统[16],见图4.x、z坐标分别是水平方向和垂直方向,代表小车和重物的运动自由度;M为小车质量(kg);m为重物质量(kg);F为驱动装置对小车的驱动力(N);l为绳索长度(m);ρ为绳索拉力(N);θ为重物摆动角度(rad).

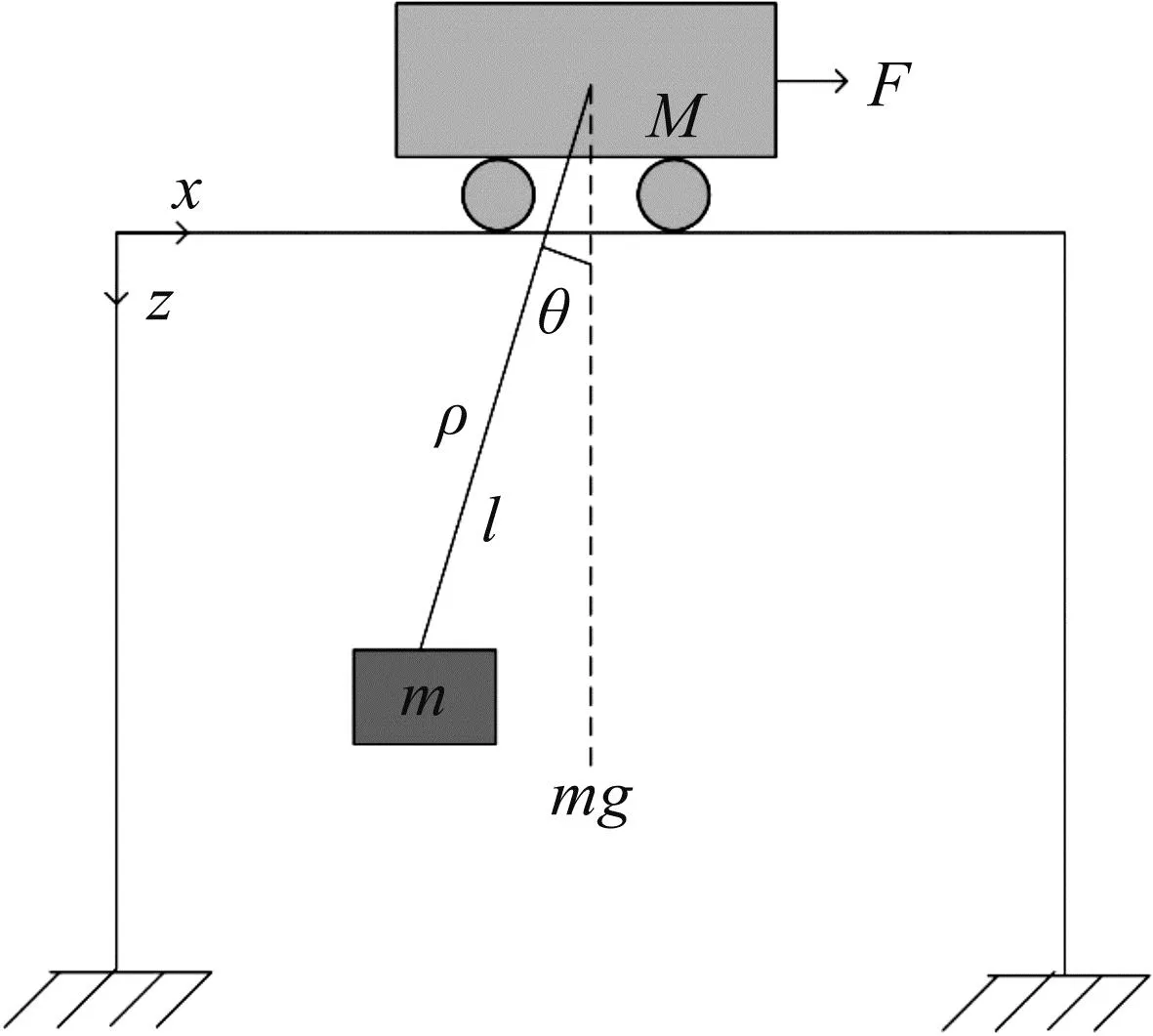
图4 桥式吊车系统的结构图

小车和重物的运动会导致重物摆动,故由动力学方法可以得出小车和重物的运动方程式：

小车的运动方程式为：

(1)

其中,xM为小车的运动位移(m).

重物在垂直方向的运动方程式为：

(2)

重物在水平方向的运动方程式为：

(3)

其中,zm为重物在垂直方向的位移(m),xm为重物在水平方向的位移(m).

在小车运动中,若连接重物的绳索长度不变,则可得出小车和重物的运动位移与绳索的方程式：

xM(t)+lsinθ=xM(t),

(4)

zM(t)=lcosθ.

(5)

消去上述式(1)～(3)的中间变量ρ,并假设θ(t)在平衡点附近(θ(t)=0)运动,可得：

(6)

(7)

经简化,本系统认为,驱动小车的电动机是一个时间常数为Td的一阶惯性环节.由此可得到驱动力F(t)与控制电压v(t)的关系满足方程式：

(8)

其中,Av为放大系数(N/V).

(9)

(10)

2.3 桥式吊车控制系统的性能

对建立的桥式吊车系统的状态空间模型进行能观、能控和稳定性分析,系统的部分参数见表1.在仿真中,只需输入系统相应的参数,点击“能观、能控、稳定性分析”按钮,即可得到仿真结果,见图5.由于能控性判别矩阵QC满秩,故系统能控;由于能观性判别矩阵QO满秩,故系统能观;由于系统特征值实部大于等于0,故系统不稳定.

表1 桥式吊车系统的参数

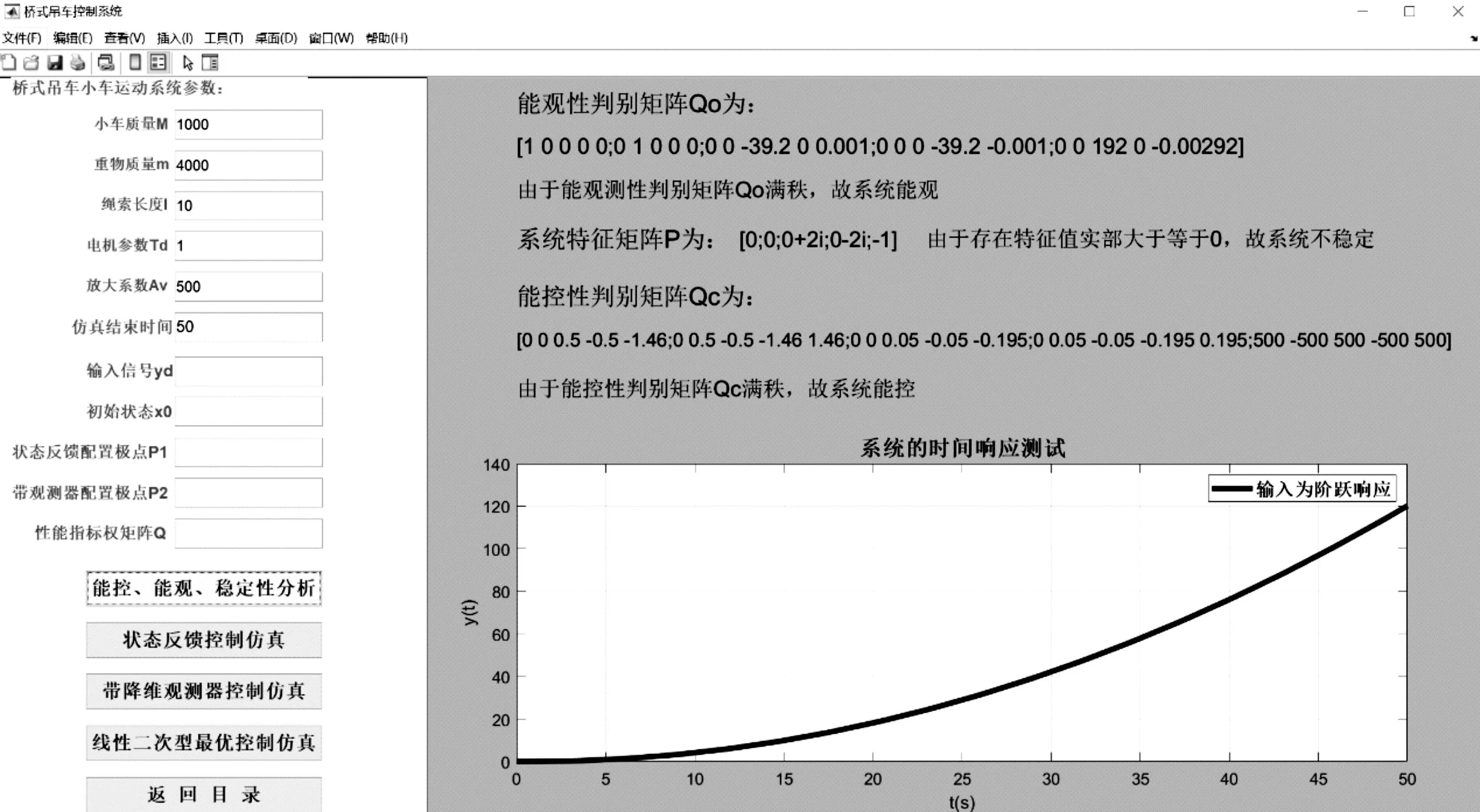
图5 能控、能观、稳定性分析

2.4 桥式吊车控制系统的跟踪控制

由图5可知,该系统能观、能控、不稳定.为系统稳定工作,需对其进行跟踪控制设计.本平台可实现状态反馈跟踪控制、带观测器跟踪控制和线性二次型最优跟踪控制仿真.本文以状态反馈跟踪控制仿真为例,在桥式吊车仿真控制界面,只需输入系统相应的参数、状态反馈配置的极点,点击“状态反馈控制仿真”按钮,即可得到状态反馈矩阵与输入变换矩阵的系数,并给出具有输入变换的状态反馈控制系统的控制结果曲线,见图6.由图6可知,在具有输入变换的状态反馈控制下,小车大约经过25 s从起始位置(2 m)无超调地运动到终止位置(10 m);重物的摆动角度从初始角度(0.1 rad)开始,保持在一个较小范围内(-0.04～0.1 rad),最终稳定地停留在预定位置(xM=10 m).其控制结果令人满意.

图6 状态反馈控制仿真

3 结 语

本文根据《线性系统理论》的课程内容,设计了一个简便且无编程要求的仿真实验平台.该仿真实验平台利用Matlab的先进数字计算和仿真功能,实现控制系统模型的建立、分析、综合设计.本仿真实验平台将原本抽象、难懂的系统理论直观化、具体化,减小了学生的学习难度,并加深了学生对线性系统理论内容的理解.桥式吊车系统综合设计的应用,提高了学生综合运用理论知识解决实际问题的能力.该仿真平台还可辅助教师进行直观教学,提高课堂的教学效率和学生的学习积极性.