基于“生成学习”理论的数学解题教学
——以2023年全国数学新高考Ⅰ卷第6题为例
2024-03-14蒋伟杰
蒋伟杰
(象山中学,浙江 象山 315700)
在传统数学解题教学中,教师往往给出自己精心准备的教学内容和教学设计,很少和学生的已有经验相结合,导致学生的主观能动性没有发挥出来,对新知识的认识不够全面.因此,重塑数学解题教学的理念、改进数学解题教学的方式是当下亟须开展的.生成学习理论下的数学解题教学重视学生的思维活动与经验基础,引导学生根据已有经验,自主构建知识体系,优化学生的认知加工过程,提升学生的综合思维能力.
1 生成学习理论的内涵
1.1 生成学习
“生成学习”又称为生成性学习,是指加州大学的维特罗克提出的学生学习生成过程(generative process)模式.生成学习理论最基本的观点是学习发生于学习者对新信息进行适当认知加工的过程.它的形成有两个前提条件:第一,人们生成对所知觉事物的意义,与其之前的知识经验相结合;第二,人脑会主动筛选一些有用信息,建构对输入信息的理解,并从中得到结论.简单来说就是人们总是倾向于利用头脑中长时间的记忆,提取与新获取的信息相关的事实,对其进行适当地加工,建构新获取信息与已有经验之间的联系,使得新获取的信息有具体的意义.在生成学习的过程中,学生不是知识的被动接受者,而是能够发挥主观能动性进行学习的个体.同时,在生成学习的过程中,已学习的知识也有着重要的价值,学生倾向于借助已有的认知学习新知识,因此,学习成果不仅依赖于外界因素的作用,学生的已有知识也在一定程度上影响着学习成果.
1.2 生成教学
“生成学习”既包括学习者的生成学习,也包括教师对学习者的学习做一个生成教学指导.该学习模式不仅可以指导学生如何学习,也可以用于指导教师的教学过程.维特罗克认为学生的学习首先是一个内在的建构和生成的过程,因此,教师最重要的作用不是组织和表述知识,而是对学生内部的意义生成过程的有效引导[1].从短期的教学效果来看,教师要引导学生建构课堂所学知识各部分之间的关系,以及建构课堂所学知识和已有学习经验之间的联系.从长期的教学目的来看,教师要培养学生学习上的主动性和能动性,引导学生掌握具体的认知策略,这对学生学习方式的转变具有重要的指导作用.
2 生成学习理论对数学解题教学的意义
2.1 善用已有经验,避免思维定式
生成学习发生的一个前提条件是与其之前的知识经验相结合.《普通高中数学课程标准(2017年版)》明确将数学基本活动经验纳入课程目标并指出,通过高中数学课程的学习,学生能获得进一步学习以及未来所必需的数学基础知识、基本技能、基本思想、基本活动经验[2].事实上,已有知识经验是把双刃剑,具有正向引导和负向引导的双重作用:一方面,学生根据已有的经验,选择熟悉的解题方向,在思路的形成上没有太多的障碍,为后续的学习奠定了较好的认知基础;另一方面,思路会被已有经验所限制,很难跳出固有思维获取新的解题思路,从而形成思维定式,不利于学生挖掘新的解题方法和接受新的思想方法.简而言之,解题教学中,既要合理运用已有经验,思维又不能陷入其中.
2.2 构建思维网图,培养知识体系
生成学习理论下,学习者能够将知识进行融会贯通,不仅能够熟练运用所学知识,还能将知识进行迁移,建构基于已有知识的框架体系.所谓知识体系,是把大量不同的知识点系统、有序、指向性明确地组合成某种类型的知识架构.教师在教学中,经常会得到学生的反馈:平常作业都会做,但是一到考试就答不出来了.其中的一个原因是学生没有形成知识体系,只是掌握了碎片化、零散化的知识,这样的学习不是生成式的,而是被动接受式的,导致在考试中解决综合性较强的问题时,不能对知识进行合理的迁移.虽然在短时间内能够记住更多的知识,但是这些知识难以长久地储存,其学习还是停留在对新接受知识的简单套用,与生成学习还有很大一段距离.为了使学生能够较好地理解所学知识,需要进一步构建该信息的意义,即引导学生将思维过程中的知识和方法进行回顾,帮助学生建立已有知识的框架体系,提高学生的思维水平.
2.3 注重思维引导,合理联想启发
生成学习理论下的“生成教学”也对教师提出了更高的要求.教师上课的落脚点不是把知识点讲清楚,而是要引导学生建构各个知识点之间的关联.对教师而言,在教学中积累的大量经验,会让其有更多的应试技巧,这些技巧会导致教师在课堂中独掌“话语权”.这样的课堂,教学效果可能是立竿见影的,学生可以较好地解决这堂课的课后习题,因为这堂课的知识点教师已经讲得很清楚了,但是不利于培养学生的能动性和主动性,学生没有形成一套自己的知识体系,这样的必然后果是学生“一听就会,一考就错”.
3 教学实践案例
根据生成学习理论和学生的认知现状,笔者以2023年全国数学新高考Ⅰ卷第6题为例,进行教学活动设计.
3.1 关联学生旧知,唤醒经验原则
例1过点(0,-2)与圆x2+y2-4x-1=0相切的两条直线夹角为α,则sinα的值为
( )
(2023年全国数学新高考Ⅰ卷第6题)
课堂上有十余位学生的解答过程是:设直线方程为y=kx-2,由于圆心到直线的距离等于半径,即
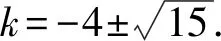
生成式学习发生的一个必要前提是学生尝试用已经学习过的知识经验解决新遇到的问题.虽然结果是错的,但是教师不要急着否定学生或者马上灌输自己的想法.这是在教学中经常会遇到的情况:学生先入为主,根据获取的新信息,在脑海中提取所需的内容,提取的内容虽然与新获取的信息比较相近,但是学生并不会仔细考虑提取的内容是否真的适合用来解决这道题目,此时学生犯了典型的“经验主义”错误.
作为教师,要引导学生分析上述解法的优点和存在的问题,组织学生进行小组讨论,提出合理的解决策略.学生提出的具体策略如下.
策略1看到直线与圆相切,除了要想到“d=r”,也要想到垂直和一组全等三角形.
策略2处理解析几何问题,避免用代数无脑运算.
策略3要有前瞻性,判断建立的方程是否容易求解、表达式的运算是否能够优化.
策略4注重数形结合,代数问题可以从几何的层面直观理解,几何问题也可以从代数的角度具体呈现.
……
首先,学生提出的策略并不一定都是对的,教师要“取其精华,去其糟粕”,总结几条合理的策略;其次,策略不一定适合所有学生,学生需要结合自己的实际情况,建构新获取信息与已有经验之间的联系,对新获取的信息进行适当加工,使其有具体的意义.生成学习就是不断建构的过程,如果能够把正在学习的内容和学生已有的相关知识经验联系起来,可以帮助学生获得对新知识的深入理解.
3.2 创设教学情境,构建知识体系
生成学习的落脚点不是解决一道题,而是要培养学生构建知识体系的能力.因此,数学解题课堂设计要立意高远,着手点要低,知识点指向要明确,即对所学内容进行再认识、再建构,用一条线索把散落各处的旧知识像珍珠一样串起来.教师可以对例1进行如下变形,让学生在不同的情境中体会数学思想产生和形成的过程.
变式1若P是直线y=-x-3上的动点,过点P与圆x2+y2-4x-1=0相切的两条直线的夹角为α,当α最大时,sinα的值为______.
变式2已知A,B是两个定点,P是直线上的动点,当点P运动到何处时,sin∠APB有最大值?
变式3设点A(1,0),B(4,0),点P为圆x2+y2-4x-1=0上的一个动点,则sin∠APB的最大值为______.

图1
在生成学习理论指导下,3个变式均以“相切时的夹角最值”为线索,着力构建本堂课的难点:“一动点两定点”模型,即A,B是两个定点,P是直线上的动点,求当点P运动到何处时∠APB有最大值(如图1).该模型在知识点上串联了“直线与圆的位置关系、三角函数中的二倍角、两角差的正切公式”等,在思想方法上串联了“数形结合、动态问题静态化、代数问题几何化”等,致力于帮助学生构建解决一类几何问题的知识体系.在现阶段的学习模式下,为了巩固某个知识点,学生会进行大量重复的机械运算,容易忽视各个题目内在的联系.教师要引导学生建构本堂课所学知识各部分之间的关系,以及建构本堂课所学知识和已有学习经验之间的联系.
如果时间允许的话,教师在课堂上也可以组织学生以同桌为单位,在例1的基础上进行变式训练.想要得到一道合理的变式题,对学生的要求较高,需要整合不同单元的知识点,厘清知识间的内在联系,此过程可以鼓励学生大胆创新,开拓思维.
3.3 在问题解决中提升数学思维水平
数学解题教学不能仅停留在“就题论题”的层面.实践证明,重复地大量做题不仅容易导致教学碎片化,学生无法形成系统的认知,而且容易陷入“题海”,无法自拔[3].数学问题的形式不会一成不变,几何图形也不会一模一样,因此,在解题教学中,不能要求学生对模型进行死记硬背,而要学会分析模型如何建构、思想方法如何生成的过程,能够对生成学习的过程进行迁移,把所学的知识迁移到新的环境和挑战中,经历问题解决的过程.
例如,课后学生命制了一道这样的题目:

这是以直线与圆为背景命制的题目,解题用到的知识是圆与圆的位置关系.基于对例1的思考,学生重构了题目情境,培养了创新精神,在命题和解题的过程中,学生会主动筛选一些有用信息,建构自己对题目的理解,这个过程就相当于生成学习中的认知加工过程.
总之,生成学习理论下数学解题教学的关键在于联系学生的已有经验,引导学生构建知识体系.生成教学要求教师用合理的联想和启发的方法,使学生的思维活动跳出“就题论题,就知识点论知识点”的层面,上升到解决问题的结构化和系统化的层面,实现解题教学的更高层次目标.
