基于软阈值降噪的脉冲卷积神经网络轴承故障诊断方法

李 浩 黄晓峰 邹豪杰 孙英杰

基于软阈值降噪的脉冲卷积神经网络轴承故障诊断方法

李 浩1黄晓峰1邹豪杰2孙英杰1

（1. 湖南工业大学轨道交通学院，湖南 株洲 412007； 2. 湖南工业大学计算机学院，湖南 株洲 412007）

针对工业场景下滚动轴承信号易受噪声干扰，导致故障诊断准确率低和稳定性差的问题，本文提出一种基于软阈值降噪的脉冲卷积神经网络诊断方法。该方法使用软阈值滤波去噪，运用带时间标签的卷积层处理二维信号，增强动态特征提取能力。同时，通过引入IF和LIF神经元实现对时域和频域信息的联合编码，并采用替代梯度法进行端到端训练。实验结果显示，在信噪比为6dB时，所提方法的诊断准确率达100%，在信噪比为-6dB时诊断准确率达77.33%，优于其他常用方法，表明所提方法在噪声下具有良好的诊断效果和稳定性。

故障诊断；软阈值；脉冲神经网络（SNN）；替代梯度法

0 引言

以轴承为关键部件的旋转机械设备约占工业设备的40%[1]。轴承故障可能导致设备停机、损坏甚至事故。然而，旋转机械的实际工作环境复杂多变，用于轴承故障诊断的振动信号易受到噪声干扰，严重影响诊断的准确率和稳定性。因此，研究噪声干扰下的轴承故障诊断对保障设备运行安全、降低维修成本、提高设备效率和延长设备寿命都具有重要意义。

复杂的背景噪声常对传感器采集的信号造成干扰，需要综合运用信号处理方法与设备特性和专家知识，对关键的故障特征进行提取[2]。然而，传统信号处理方法如小波变换和频谱分析仅能识别显著特征，存在一定的局限性。

近年来，随着深度学习的快速发展，越来越多的学者将其应用于故障诊断中。基于深度学习的端到端训练方法，可以直接处理复杂的轴承振动信号，实现故障模式的自动识别。相比传统方法，深度学习技术避免了手工特征工程的限制，使故障诊断更加智能化和准确化。常用的基于深度学习的故障诊断方法包括堆叠降噪自动编码器（stacked denoising auto encoder, SDAE）、卷积神经网络（convolutional neural networks, CNN）、门控循环单元（gated recurrent unit, GRU）、对抗神经网络（generative adversarial networks, GAN）等[3-6]。

文献[7]将卷积神经网络和长短期记忆网络应用于光伏系统的故障识别，有效识别了双重故障同时存在的情况。文献[8]将声音信号通过连续小波变换转化为时频图，结合卷积神经网络实现了对柱塞泵磨损和松动故障的诊断。文献[9]提出的自适应聚合网络模型，将随机抽样作为数据输入策略，并结合CNN、GRU和注意力机制，大大提高了网络的抗噪声和域适应性。文献[10]提出一种基于格拉姆角场和小尺寸卷积的胶囊网络轴承故障诊断分类方法，解决了一维振动信号在输入卷积神经网络时无法充分提取相对位置关系的问题。文献[11]提出一种基于卷积神经网络和长短期记忆神经网络的双输入模型，同时使用时域和频域特征在变负载和噪声条件下，实现了较高的故障识别率。文献[12]提出一种基于堆叠倒残差卷积神经网络的智能轴承故障诊断方法，保证了模型在噪声环境下的准确性。文献[13]采用自适应小波分解和卷积神经网络结合长短期记忆方法对噪声环境下的齿轮箱进行精确故障诊断，具有较高的抗噪能力和训练精度。文献[14]提出一种深度三流网络和一种小波权重初始化方法和平衡动态自适应阈值算法，并在四个数据集上得到了有效验证。

为了更好地模拟生物神经元的工作原理，第三代神经网络——脉冲神经网络（spiking neural networks, SNN）应运而生[15]。SNN采用更符合生物神经元放电机制的脉冲编码和时序处理方法，使神经元能够实时响应输入，并且仅在输入发生变化时消耗能量。因此，SNN能够更快地处理和反馈输入信息，比传统CNN模型更节省计算资源和能源消耗。此外，SNN还可以通过时间间隔、脉冲频率等时间因素对信息进行编码和处理，这使它在处理与时序相关的任务中具有优势。因此，将SNN应用于轴承振动信号的故障诊断是较为合适的选择。ZUO Lin等[16]提出基于SNN的轴承故障诊断方法，通过局部均值分解（local mean decomposition, LMD）从原始振动信号中提取的特征被编码为尖峰，使用改进的时间加速器学习规则训练SNN，实现了较高准确度的轴承故障诊断。

尽管上述文献在各自场景中取得了相对不错的轴承故障诊断效果，但对于轴承故障的诊断仍存在以下问题：

1）在保持高诊断率的同时，如何确保较好的稳定性，仍需要进一步研究。

2）对于含噪信号的轴承故障诊断，表现出诊断准确率一般且不稳定的特点，如何增强算法的抗噪性、鲁棒性，以及加强算法提取深层特征的能力，仍有待进一步研究。

本文提出一种基于脉冲卷积神经网络的端到端诊断方法。首先，将原始轴承振动信号进行切片和调整，转换为二维矩阵作为网络输入。然后，利用软阈值（soft thresholding）编码层对输入进行滤波，用可学习的软阈值函数去除噪声干扰，保留有用的故障特征。接着，带时间标记的卷积层可直接处理二维矩阵输入，同时学习提取时域和频域特征。为了增强模型对动态信号的处理能力，导入IF（integrate-and-fire）神经元增加时间相关性，实现自适应脉冲特征编码。经池化层降维后，全连接层结合LIF（leak integrate-and-fire）神经元进行分类预测。最后，根据输出层神经元的脉冲发放频率分布，判定所属的故障类别。与此同时，使用均方误差（mean square error, MSE）损失函数进行监督训练，通过替代梯度法迭代优化模型参数。

该端到端训练的模型融合了时域编码与频域特征提取技术，本文利用公共数据集进行分析，以验证该模型在强噪声干扰条件下的故障诊断效果和稳定性。

1 理论基础

1.1 脉冲神经网络

脉冲神经网络是一类更贴近生物神经系统、信息编码更丰富、计算更高效的神经网络模型。SNN中，神经元之间通过脉冲（spikes）进行通信和信息编码。每个脉冲都记录一个精确的发放时间，信息被编码在脉冲的时间序列中。此外，SNN是动态的网络，连续不断地处理输入脉冲并产生输出。信息被编码在时间维度上，而不是简单的激活值。

SNN最常使用IF模型和LIF模型来模拟神经元的积分发放行为。这类模型简单实用，通过积分输入脉冲决定输出脉冲发放。IF是最简单的积分发放模型，其神经元的膜电位变化过程可用RC电路表示，IF模型等效电路如图1所示。其中，()为所有突触前神经元放电所产生的突触电流之和。IF神经元膜电位最初处于静息电位reset，通过接收输入脉冲电流，电荷在电容器中不断积累，导致神经元内部的膜电位()不断增大。当膜电位()累积到阈值th时，神经元将发放一个输出脉冲，发放后膜电位()逐渐衰减到静息电位reset。

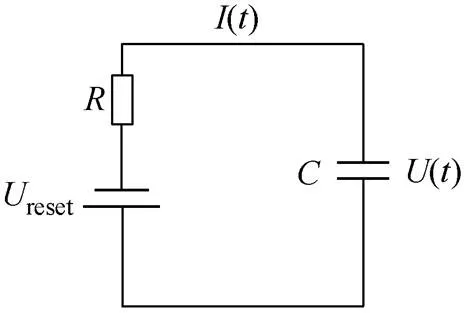
图1 IF模型等效电路

IF神经元模型因结构简单、能够模拟生物神经元的基本积分发放过程而被广泛使用。但是，IF模型存在以下缺陷：无法模拟神经元的电压泄漏机制；发射频率与输入无关；缺乏抑制性突触的模型；发射机制过于简单化。

为了弥补IF模型的不足，LIF模型被提出，也被称为“积分泄漏发放”模型。LIF模型在IF模型的基础上添加了电压泄漏机制。神经元会积累输入信号，并随时间的推移逐渐恢复到静息电位。当膜电位达到阈值时，神经元会发放一个脉冲，并将膜电位重置为初始状态。LIF模型更准确地描述了生物膜电位的动力学过程，成为目前最受欢迎的脉冲神经元模型之一。LIF模型对应的膜电位微分方程为

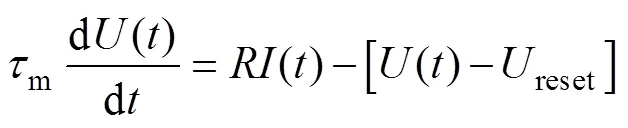
1.2 替代梯度法

由于SNN的峰值函数是一个阶跃函数，输出只有0或1，除零点以外的点的导数都为零。而梯度下降法采用递增式参数更新，从负梯度方向逐步逼近最小值，依赖损失函数的梯度来更新参数，若梯度为0，则无法反向传播误差更新参数。阶跃函数（step function）等不可导函数作为激活函数时，不能直接使用梯度下降法进行优化，需改用其他优化算法对具有不可导激活函数的网络进行训练。

文献[17]描述的替代梯度法利用一个可微的激活函数来逼近峰值函数，可以解决上述问题。但是，此方法不易得到神经元模型的解析解，不利于训练的进行，这里采用具有离散参数的动态神经元模型对SNN神经元进行数值模拟[18]。在脉冲神经元中，膜电位()由两点组成：当前输入()和上一个时间步的终点电位(-1)。以LIF神经元为例，用离散的微分方程近似连续函数，充电过程可写为

用()表示放电前的瞬时电位，有

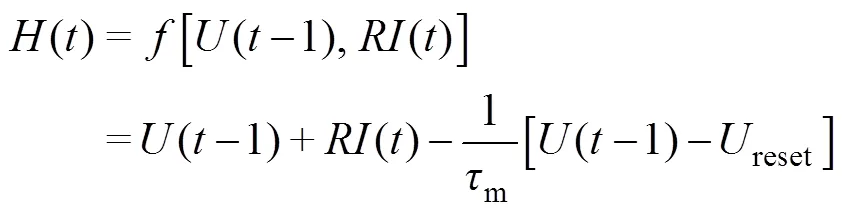
当膜电位大于阈值时，释放脉冲，放电过程可写为

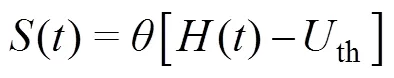
放电后，恢复到静息电位，复位过程可写为

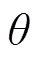
1.3 软阈值法

软阈值函数是信号去噪算法的重要组成部分，可与神经网络结合使用，抑制数据中的噪声，帮助模型提取有用的特征信息。软阈值函数的定义如式（6）所示。

噪声信号在小波域的能量较为分散，而原始信号聚集在少数大的小波系数中。软阈值降噪算法基于此原理，采用连续惩罚函数对小波系数进行处理，相较于硬阈值直接置零，可更好地保留原始信号的细节信息。具体而言，该算法首先采用小波变换将信号转换到小波域，然后对小波系数的幅值进行软阈值处理：小波系数的幅值若低于设定阈值，则减小其幅值；若高于阈值，则保持不变。最后对处理后的小波系数进行逆变换，得到降噪后的信号。

软阈值降噪算法具有计算效率高、易于实现及可对信号进行较好保护的优点，能够有效抑制信号中的噪声，并保留信号的主要特征。因此，在图像去噪、语音信号处理等领域得到广泛应用。

2 所提算法

2.1 总体框架

本文所提模型为基于软阈值降噪的脉冲卷积神经网络轴承故障诊断模型，简称STSNN模型，其故障诊断流程如图2所示。

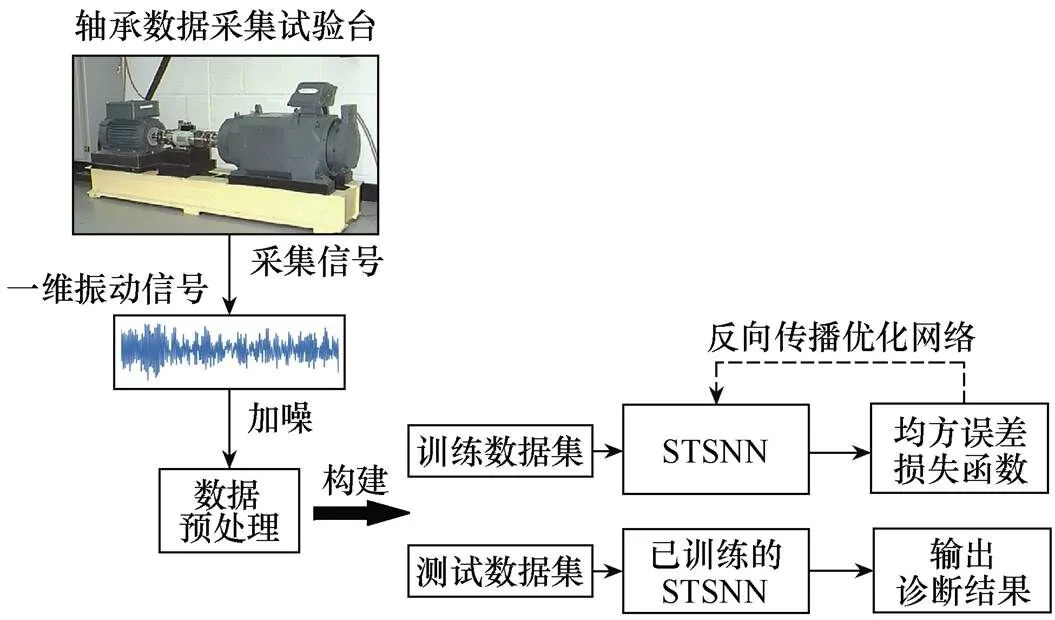
图2 STSNN模型故障诊断流程

STSNN模型的轴承故障诊断主要包含以下步骤：

1）数据采集。通过专业的轴承故障试验台采集数据，这里选用的是公用数据集。

2）数据处理。读取原始振动信号，切片，将数据从一维转化为二维，进行随机打乱和数据归一化处理，按4:1的比例划分为训练集和测试集，并将不同故障的数据集进行叠加。

3）编码成脉冲信号。使用IF模块将输入的二维信号编码为脉冲序列。

4）时空特征提取。通过卷积层、池化层、Softshrink层等提取信号的时空特征，得到编码后的特征映射。

5）分类。将特征打平并送入全连接层，其输出通过LIF模块转换为脉冲发放频率，判断出轴承故障类型。

6）循环迭代，优化模型。通过多轮循环比较模型输出和真实标签计算损失函数值，反向传播优化参数来减小损失，逐步提高模型性能，优化损失 函数。

2.2 STSNN架构

STSNN模型架构如图3所示，主要由软阈值模块、脉冲特征提取模块、全连接分类模块组成。STSNN模型的详细架构见表1。

图3 STSNN模型架构

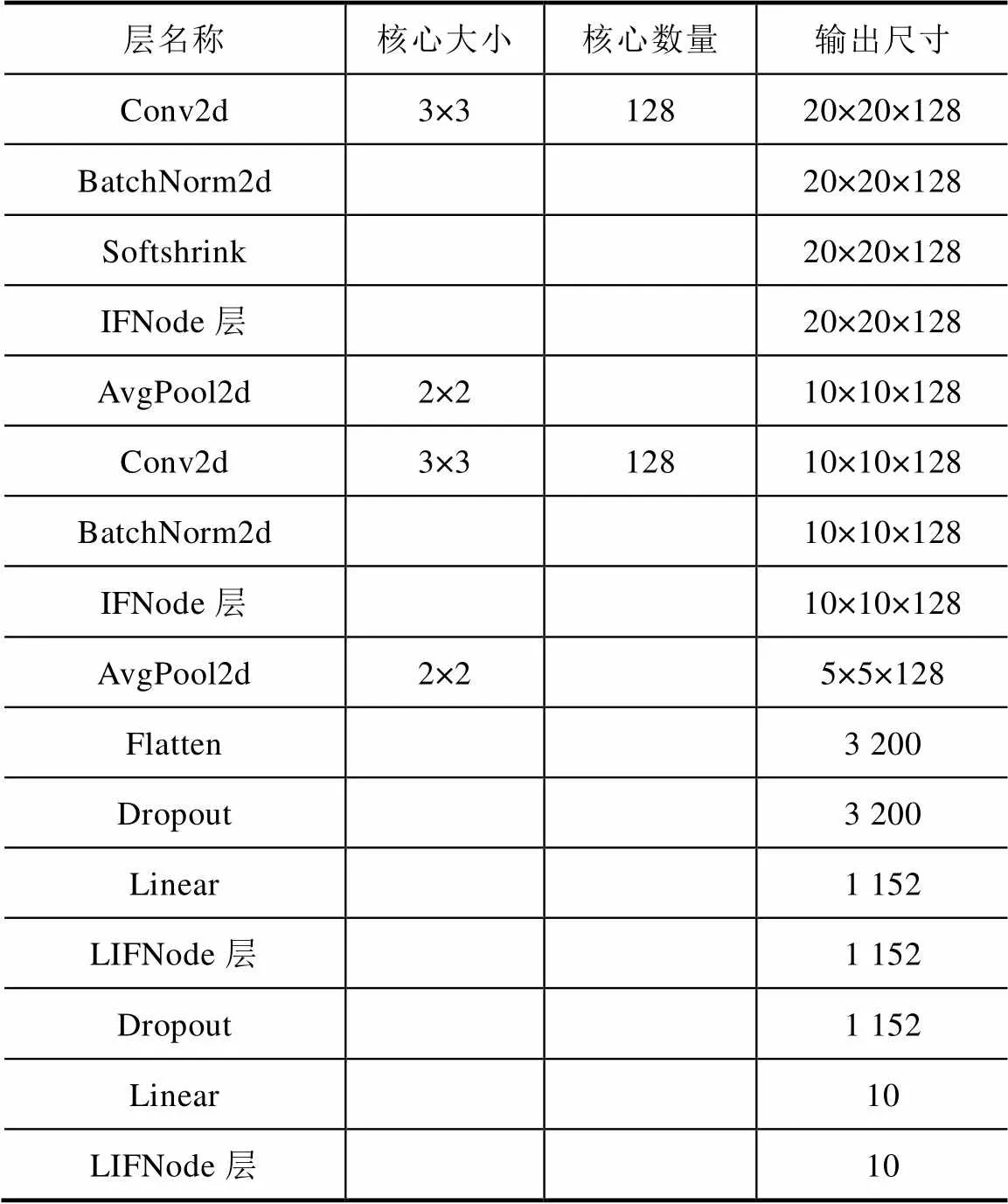
表1 STSNN模型的详细架构

1）软阈值模块

软阈值模块是由卷积层、BatchNorm层和软阈值层组成。信号首先经过卷积和归一化处理，然后传入软阈值层。在卷积层后添加软阈值层，有以下考虑：

卷积层的作用是提取不同方向和尺度的特征子带，类似小波变换的过程。软阈值处理可以抑制噪声对特征的影响，并保留有用的信息。将软阈值层放在卷积层之后，可以直接对提取到的特征系数进行处理。如果放在输入层，由于输入原始信号中含有噪声成分，软阈值层的效果不明显。如果放在网络最后，已经无法起到抑制特征层噪声的作用。将软阈值层放在卷积层之后，可以直接对特征层进行处理，有效地抑制噪声对后续网络的影响，从而增强模型的鲁棒性。

因此，软阈值模块中的软阈值层被放置在卷积层之后，以确保在平滑去噪的同时能够保留有用的信号特征，并有效抑制噪声对后续网络的影响，从而提高模型的稳定性。

2）脉冲特征提取模块

脉冲特征提取模块由2个（IFNode层+AvgPool层），以及1个（卷积层+BatchNorm层）组成，主要包括自适应脉冲编码和脉冲平均池化两步。自适应峰值编码模块由卷积层和脉冲神经元层组成，可以直接对输入信息进行编码，避免了传统SNN额外使用编码器导致的信息丢失问题。其中，数据经过卷积层后再进行归一化，防止峰值神经元层输入过载，增强网络稳定性。预处理后的振动信号与各时间步长的卷积核进行卷积。膜电位在IF神经元中逐步积累，当超过阈值电压th时，释放脉冲并恢复到静息电位reset；否则进入下一时间步继续积累。峰值平均池化保留每个感受野的明显特征，同时抑制不显著的细微特征，减少参数量和计算量，提升模型的计算效率。

该模块充分利用SNN在时域编码和CNN在空域特征提取方面的能力，提高了特征提取效率和计算效率。

3）全连接分类模块

全连接分类模块首先由Flatten层、2个（Dropout层+全连接层+LIFNode层）组成。前面已完成对信号特征的充分提取，现利用参数离散的LIF模型构建分类器网络，并引入漏出层防止过拟合。输出的脉冲信号发送到脉冲计数器。当=0, 1,…,-1时，输出峰值为()，其中为总时间步数。计算输出层神经元释放的峰值数量，除以，得到脉冲释放频率，即网络的预测输出。最后，将最高脉冲频率对应的输出神经元的分类作为诊断结果。

全连接分类模块使用两个全连接层逐步提取特征，通过计算输出层脉冲频率并选择最高频率对应的类别，实现对故障模式的智能诊断。

3 实验与对比验证

3.1 实验设备及环境介绍

实验所用深度学习框架为pytorch，电脑配置为Inter i5-13490F，32GB内存，RTX4070Ti，Windows10操作系统。对于网络参数的初始化设置，通过多次实验和经验总结，确定最终的网络参数。选取初始学习率为0.01，使用自适应矩估计（adaptive moment estimation, Adam）网络优化器，MSE损失函数。激活函数使用Sigmoid作为surrogate function。输入数据为4维张量（sample_num, 1, 20, 20），分别表示样本数量、通道数、高度、宽度，即每个样本是1通道的20×20大小。使用固定的随机种子，单次训练的样本数为50。

3.2 实验数据

为了验证本文所提算法的有效性，采用美国凯斯西储大学（Case Western Reserve University, CWRU）轴承数据集进行故障诊断分类实验。

凯斯西储大学轴承试验台如图4所示，CWRU轴承数据集的试验台由2马力电动机（左）、扭矩传感器/编码器（中间）、测功机（右）和控制电子设备（未显示）组成。实验所使用的数据集包括在四种负载条件（0hp、1hp、2hp和3hp，其中1hp= 0.745kW）下的轴承振动加速度数据，转速在1 730～1 797r/min，负载越大转速越慢。采样频率有12kHz和24kHz两种，包括正常数据，以及滚动体故障、内圈故障、外圈故障三种故障数据，每种故障分别有三种不同尺寸的故障数据，共10种。本文使用采样频率为12kHz在0hp负载下的驱动端轴承数据，用标签0～9分别表示正常及不同故障类型的10种数据，CWRU轴承故障分类及标签值见表2。

图4 凯斯西储大学轴承试验台

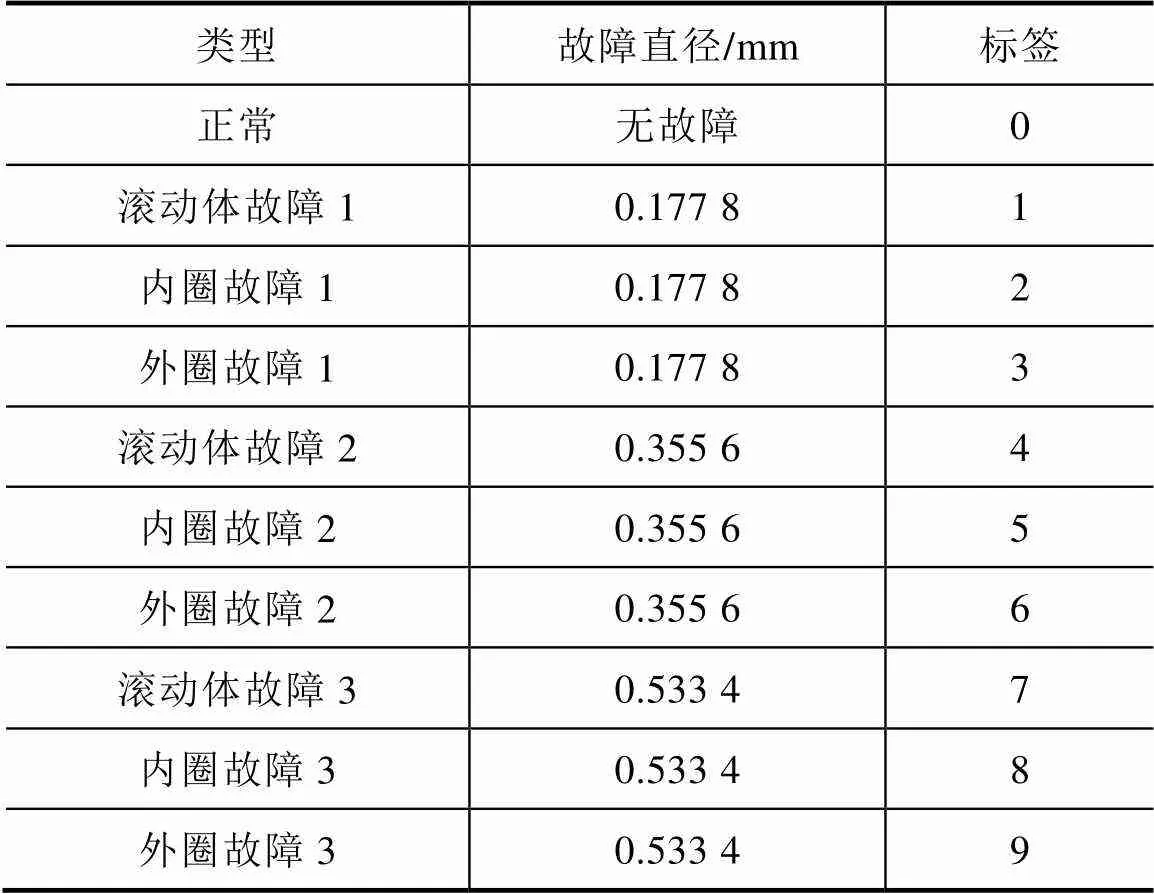
表2 CWRU轴承故障分类及标签值

其中，外圈故障数据有三个方向的数据集，本文选取六点钟方向的数据集。试验台电动机转速为1 797r/min，约30r/s，采样频率为12kHz，轴承每转一圈，采样400个样本数据。每种类型数据选取前12万个，10种共120万个数据，以20×20个数据为一组，共3 000组。先将原始一维信号叠加，并按照训练集与测试集4:1的比例划分，再将一维数据转化为二维数据，送入网络模型。

3.3 数据预处理

凯斯西储大学标签为1的数据集加入信噪比为-3dB的噪声后，部分信号对比如图5所示，可见加入噪声后的信号基本覆盖了原始信号，特征表现得不是很明显，需要诊断模型具有较好的特征识别 能力。

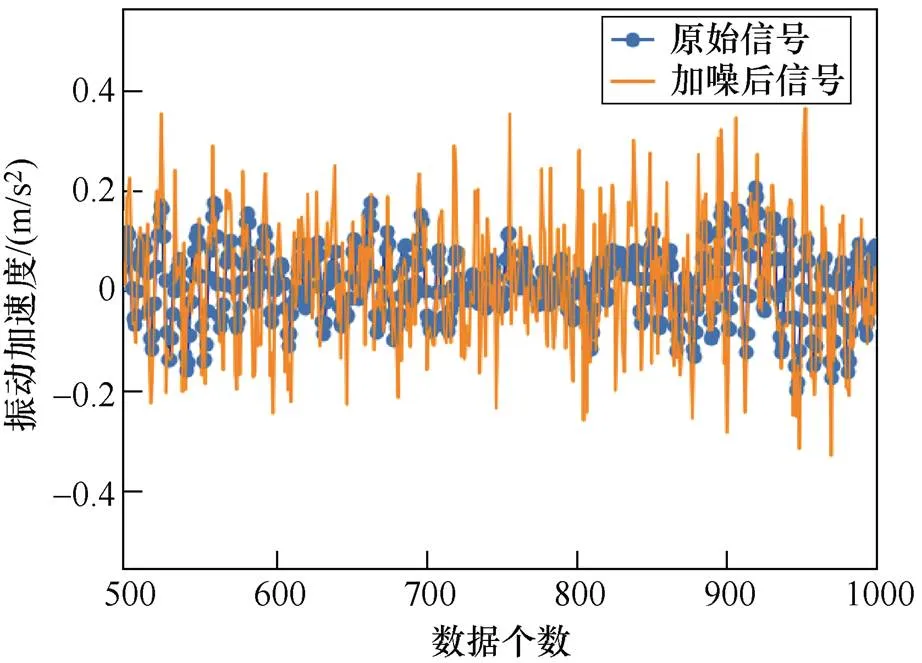
图5 加噪前后的信号对比

3.4 实验结果分析

为了验证所提方法在不同信噪比下的鲁棒性，在五种信噪比下进行实验，计算得到训练准确率与损失值。不同SNR噪声下所提方法的训练准确率和损失值分别如图6和图7所示。

图6 不同SNR噪声下所提方法的训练准确率

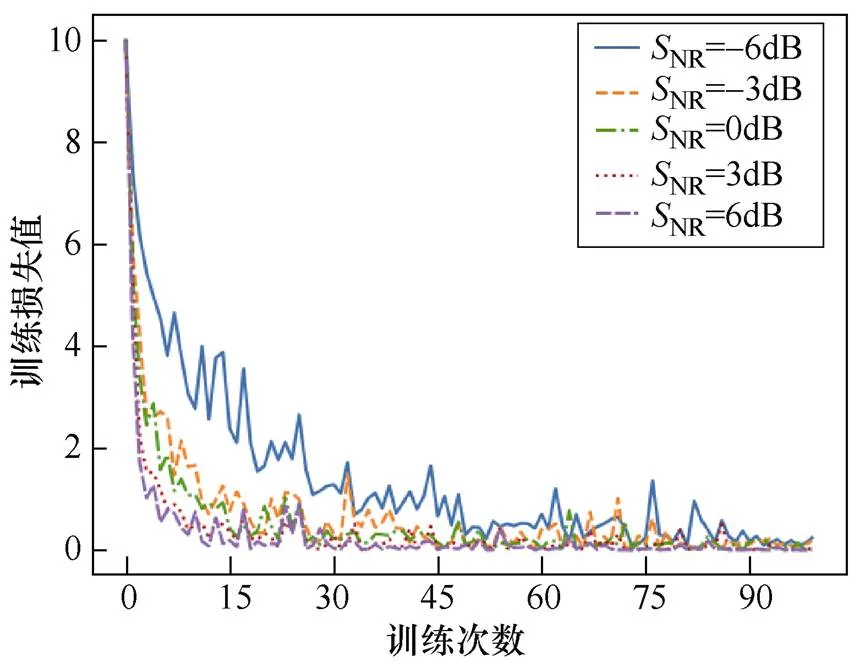
图7 不同SNR噪声下所提方法的训练损失值

信噪比越大，表示信号中的噪声越少，模型更易从信号中提取出故障特征，实现故障分类。从图6和图7可以看出，随着信噪比的增大，信号中的故障特征更加明显，模型在故障诊断任务中的表现随之提升，具体表现为：在较短时间，准确率达到最大值并趋于稳定，损失值快速下降并趋于稳定。

上述结果表明，在噪声较高的环境下，所提出的模型仍然能够保持较高的准确率和较低的损失值，该模型在噪声环境中表现出较好的稳定性和鲁棒性。

3.5 不同方法对比分析

为了评估所提方法的性能，在保证数据集和训练参数一致的前提下，进行对比实验，得到不同方法在不同信噪比下的诊断准确率见表3，相应的柱状图如图8所示。其中，CNN的结构和参数与本文所提模型相同；FaultNet代表文献[19]提出的一种基于CNN的三通道架构，通过平均滤波和中值滤波增加了两个通道，充分利用来自信号的信息，对含噪声的信号有较好的鲁棒性；SNN代表文献[20]提出的一种基于卷积SNN的轴承故障诊断方法，充分提取了轴承振动信号的时空特征，达到较高的分类准确度。

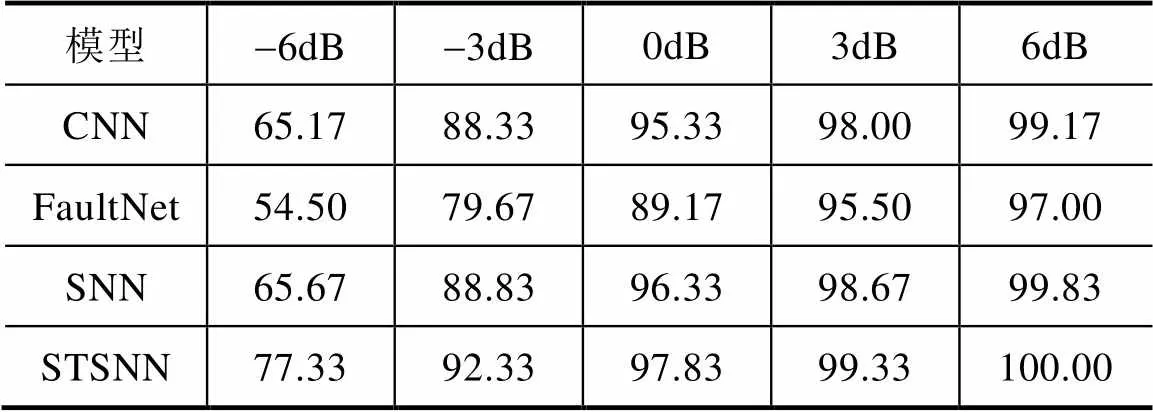
表3 不同方法在不同信噪比下的诊断准确率 单位：%

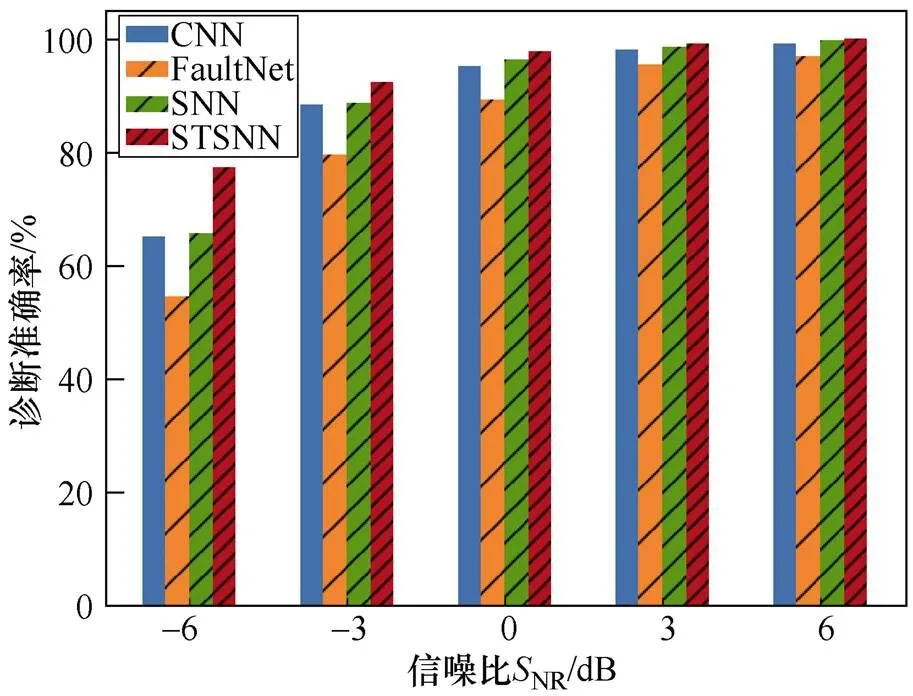
图8 不同方法在不同信噪比下的诊断准确率柱状图

由表3和图8可知，本文所提方法在不同信噪比下均表现出最优的诊断效果。在低噪声条件（信噪比大于等于0dB）下，4种方法都能达到较高的诊断准确率。其中，CNN和SNN表现相似，FaultNet表现稍差，而本文所提方法的诊断准确率可达97%及以上，效果最好。在高噪声条件（信噪比小于0dB）下，不同方法的表现差距较大，尤其是信号添加-6dB的噪声时，STSNN明显优于其他3种方法，可达到77.33%的诊断准确率，与CNN、FaultNet、SNN相比，本文所提方法的诊断准确率分别提升了12.16个百分点、22.83个百分点、11.66个百分点，表明本文所提方法在强噪声干扰下仍能较好地提取故障特征，具有良好的噪声鲁棒性。

整体来看，随着SNR的减小（信号中噪声含量增加），每种方法的诊断准确率都越来越低，证明添加高斯噪声对模型的特征提取能力具有限制作用。

由于本文所提方法主要面向强噪声背景下的故障信号诊断，故绘制信噪比分别为-6dB和-3dB时不同方法的诊断准确率如图9、图10所示。由图9和图10可见，STSNN在稳定性、快速性和诊断准确率方面均表现最佳。

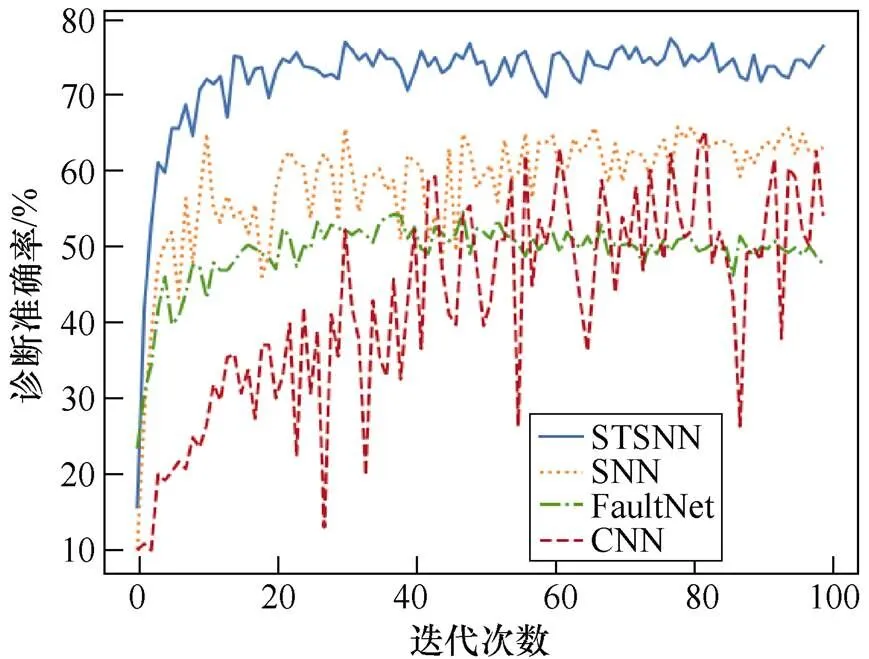
图9 信噪比为-6dB时不同方法的诊断准确率

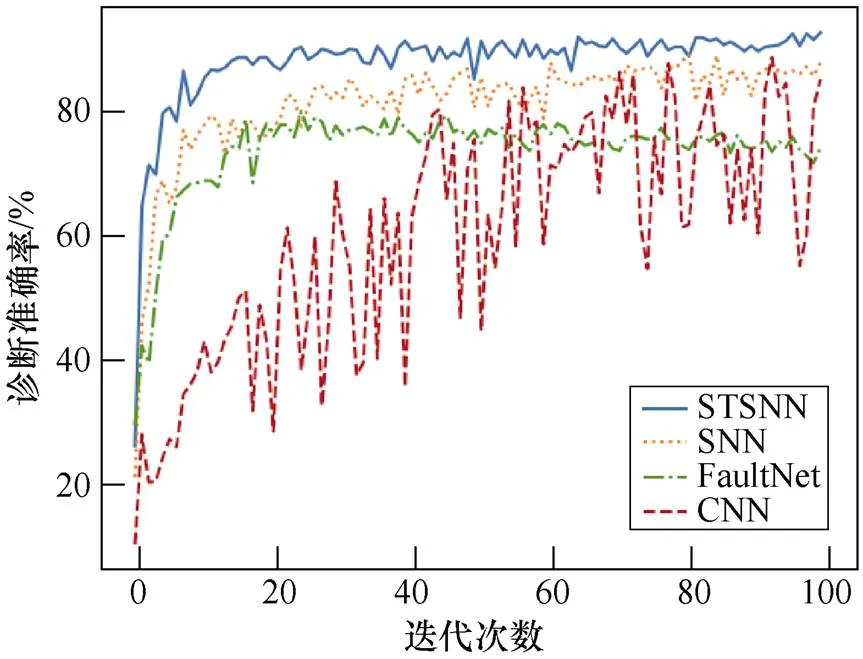
图10 信噪比为-3dB时不同方法的诊断准确率

3.6 补充实验

为了验证所提方法各部分的有效性，对基于软阈值降噪、均方误差损失函数、平均池化及Adam优化器等构建的原模型进行一系列补充实验。

针对较高噪声条件（NR=-6dB和NR=-3dB）下的故障诊断，通过控制单一变量并重复多次实验，评估有无软阈值降噪、损失函数、池化方式及优化器选择等因素的影响。对比实验的变量均为神经网络分类任务中常用的组件，实验结果见表4。

从表4可以看出，原模型的诊断准确率和损失值均优于其他模型，表明所提方法有效。其中，与没有采用软阈值的模型相比，采用软阈值降噪的模型在不同噪声下的实验结果都更好；与原模型采用均方误差损失函数相比，采用交叉熵损失函数的模型不仅诊断准确率较低，而且损失值显著偏高；采用方均根传播优化器的模型在中等噪声（SNR=-3dB）下接近原模型的性能水平，但总体而言，其诊断效果不及采用Adam优化器的原模型。

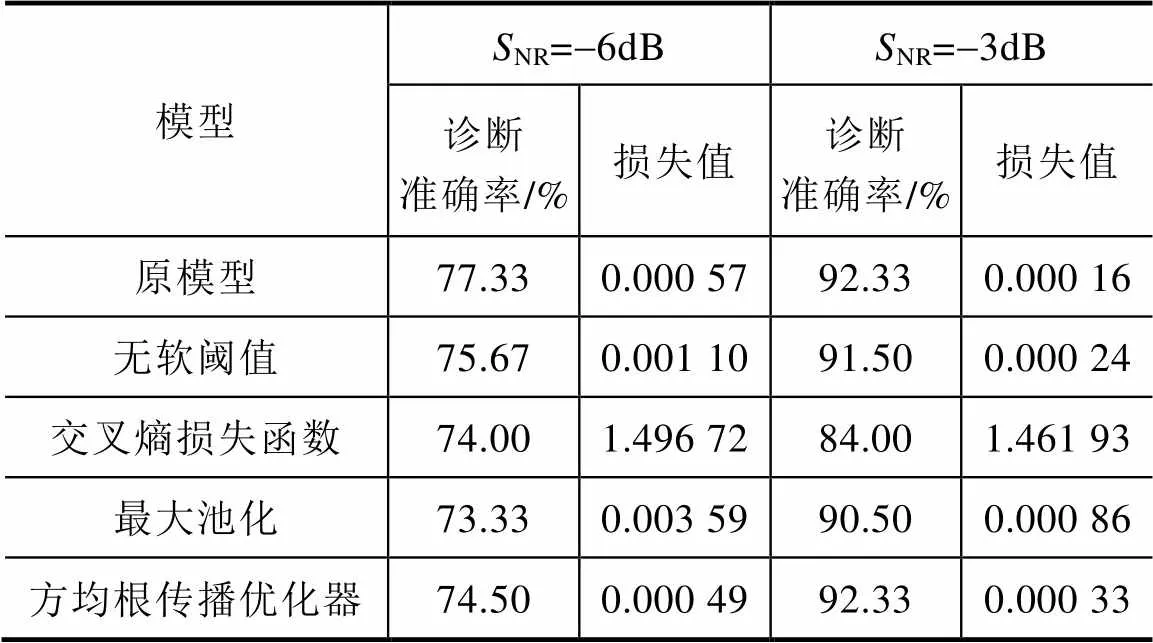
表4 实验结果

池化层既能降低模型复杂度，又能防止过拟合，在深度学习的模型中十分重要。因此，为了探讨使用不同池化方法对诊断准确率的影响，根据实验数据绘制信噪比分别为-6dB和-3dB时不同池化方法的诊断准确率如图11和图12所示。当SNR为-6dB时，平均池化法在迭代12次后趋于稳定，并在最高值附近浮动，而最大池化法需要迭代约30次才能达到此效果，并且诊断准确率明显低于前者。当SNR为-3dB时，平均池化法得到的曲线收敛更快，诊断准确率更高。

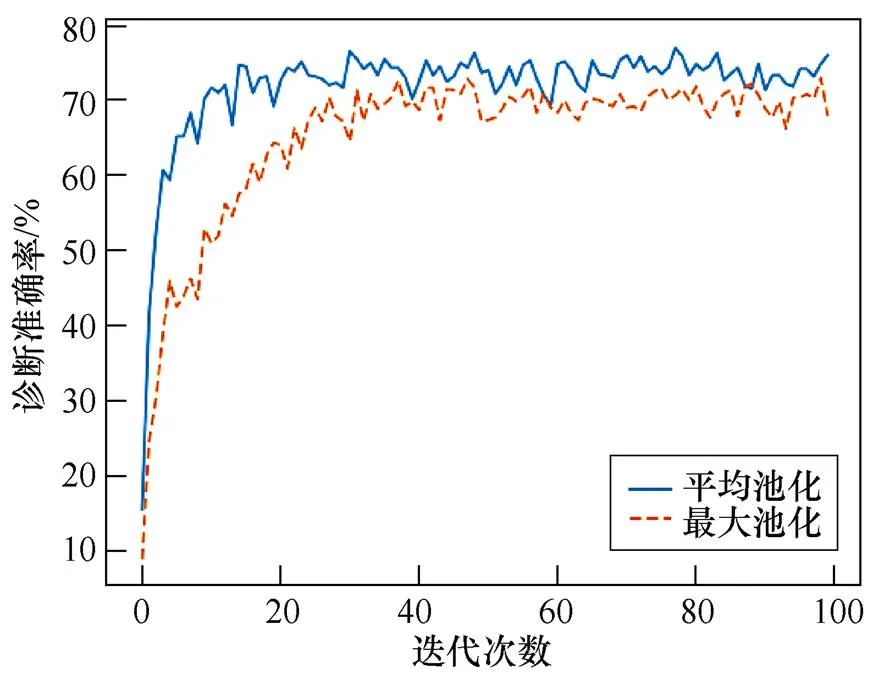
图11 信噪比为-6dB时不同池化方法的诊断准确率

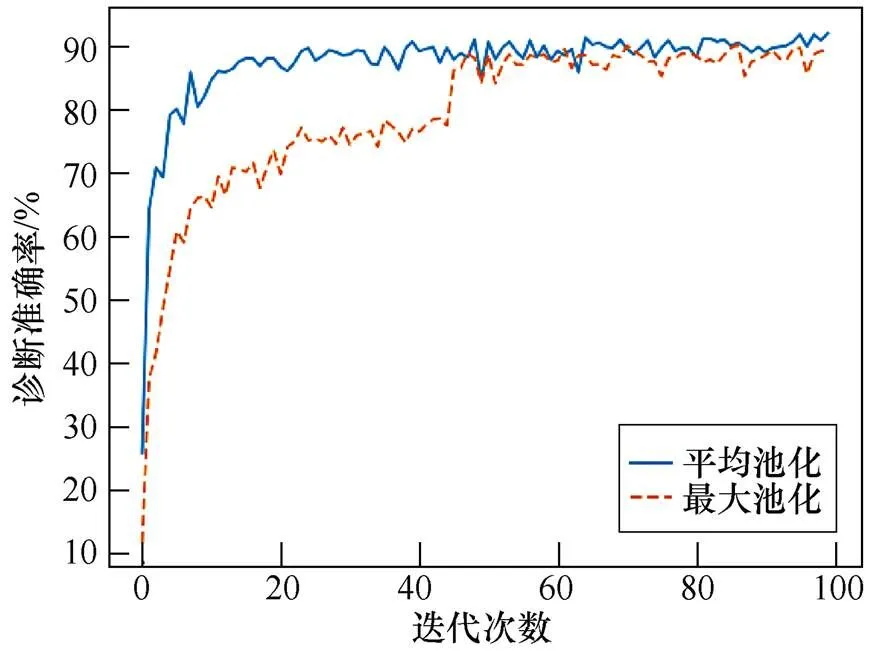
图12 信噪比为-3dB时不同池化方法的诊断准确率

以上对比实验结果表明，原模型各部分选择有效，可以得到更高的诊断准确率和更低的损失值，实现更有效的轴承故障诊断。

4 结论

针对工业场景中滚动轴承振动信号易受噪声干扰，导致故障诊断模型的诊断准确率不高且稳定性差的问题，本文提出了一种基于软阈值降噪和改进的脉冲卷积神经网络模型。该模型将软阈值应用于卷积层之后，直接对特征层进行处理，从而在平滑去噪的同时保留有用的信号特征。这种方法有效地抑制了噪声对后续网络的影响，提高了模型的鲁棒性和抗噪性，同时避免了信息损失。为了充分提取信号的时空特征，本文将时空动态特性与卷积神经网络结合，构建了该改进模型。实验中，通过给原始故障信号加入噪声，模拟了工业场景下存在的噪声污染问题，并以此验证了该模型在实际场景中的可行性。

[1] CHEN Xuefeng, WANG Shibin, QIAO Baijie, et al. Basic research on machinery fault diagnostics: past, present, and future trends[J]. Frontiers of Mechanical Engineering, 2018, 13(2): 264-291.

[2] 张军军, 陈果, 卢应强, 等. 风电场主设备预警诊断系统设计与开发[J]. 电气技术, 2023, 24(5): 52-57.

[3] 李兵, 梁舒奇, 单万宁, 等. 基于改进正余弦算法优化堆叠降噪自动编码器的电机轴承故障诊断[J]. 电工技术学报, 2022, 37(16): 4084-4093.

[4] 李志川, 兰生, 魏柯. 基于MRSVD-GRU的混合三端特高压直流输电线路单极接地故障定位方法[J]. 电气技术, 2023, 24(3): 1-8, 63.

[5] 邬春明, 朱海潮, 马欣, 等. 两级混淆对抗域自适应网络轴承故障诊断[J]. 北京交通大学学报, 2022, 46(5): 159-166.

[6] 宋向金, 孙文举, 刘国海, 等. 深度子领域自适应网络电机滚动轴承跨工况故障诊断[J]. 电工技术学报, 2024, 39(1): 182-193.

[7] 涂彦昭, 高伟, 杨耿杰. 一种基于卷积神经网络和长短期记忆网络的光伏系统故障辨识方法[J]. 电气技术, 2022, 23(2): 48-54.

[8] TANG Shengnan, ZHU Yong, YUAN Shuoqi. Intel- ligent fault diagnosis of hydraulic piston pump based on deep learning and Bayesian optimization[J]. ISA Transactions, 2022, 129: 555-563.

[9] JIN Guoqiang, ZHU Tianyi, AKRAM M W, et al. An adaptive anti-noise neural network for bearing fault diagnosis under noise and varying load conditions[J]. IEEE Access, 2020, 8: 74793-74807.

[10] 张辉, 戈宝军, 韩斌, 等. 基于GAF-CapsNet的电机轴承故障诊断方法[J]. 电工技术学报, 2023, 38(10): 2675-2685.

[11] QIAO Meiying, YAN Shuhao, TANG Xiaxia, et al. Deep convolutional and LSTM recurrent neural networks for rolling bearing fault diagnosis under strong noises and variable loads[J]. IEEE Access, 2020, 8: 66257-66269.

[12] YAO Dechen, LIU Hengchang, YANG Jianwei, et al. A lightweight neural network with strong robustness for bearing fault diagnosis[J]. Measurement, 2020, 159: 107756.

[13] 蔡超志, 白金鑫, 池耀磊, 等. 基于CEEMDAN自适应小波降噪与卷积神经网络的齿轮箱故障诊断研究[J]. 机床与液压, 2022, 50(24): 171-180.

[14] HE Chao, SHI Hongmei, SI Jin, et al. Physics- informed interpretable wavelet weight initialization and balanced dynamic adaptive threshold for intelligent fault diagnosis of rolling bearings[J]. Journal of Manufacturing Systems, 2023, 70: 579- 592.

[15] ROY K, JAISWAL A, PANDA P. Towards spike-based machine intelligence with neuromorphic computing[J]. Nature, 2019, 575(7784): 607-617.

[16] ZUO Lin, ZHANG Lei, ZHANG Zhehan, et al. A spiking neural network-based approach to bearing fault diagnosis[J]. Journal of Manufacturing Systems, 2021, 61: 714-724.

[17] NEFTCI E O, MOSTAFA H, ZENKE F. Surrogate gradient learning in spiking neural networks: bringing the power of gradient-based optimization to spiking neural networks[J]. IEEE Signal Processing Magazine, 2019, 36(6): 51-63.

[18] FANG Wei, YU Zhaofei, CHEN Yanqi, et al. Incorporating learnable membrane time constant to enhance learning of spiking neural networks[C]//2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 2022: 2641- 2651.

[19] MAGAR R, GHULE L, LI Junhan, et al. FaultNet: a deep convolutional neural network for bearing fault classification[J]. IEEE Access, 2021, 9: 25189-25199.

[20] ZHANG Changfan, XIAO Zunguang, SHENG Zhenwen. A bearing fault diagnosis method based on a convolutional spiking neural network with spatial- temporal feature-extraction capability[J]. Transporta- tion Safety and Environment, 2023, 5(2): tdac050.

Bearing fault diagnosis method based on soft threshold denoising for spiking convolutional neural network

LI Hao1HUANG Xiaofeng1ZOU Haojie2SUN Yingjie1

(1. College of Railway Transportation, Hu’nan University of Technology, Zhuzhou, Hu’nan 412007; 2. College of Computer Science, Hu’nan University of Technology, Zhuzhou, Hu’nan 412007)

The signals of rolling bearings are easily interfered by noise in industrial environments, which reduces fault diagnosis accuracy and worsens stability. This paper proposes a diagnostic method based on soft threshold denoising for spiking convolutional neural network. Soft threshold filtering for noise reduction is proposed in this paper. This paper uses time-tagged convolutional layers to process two-dimensional signals to enhance dynamic feature extraction capabilities. IF and LIF neurons are introduced to jointly encode time domain and frequency domain information, and the surrogate gradient method is used for end-to-end training. The results show that the diagnostic accuracy reaches 100% under the signal-to-noise ratio of 6dB, and still reaches 77.33% under the signal-to-noise ratio of-6dB. The results of this method have certain advantages compared with commonly used methods, which verifies that the proposed method has better diagnostic results and higher stability under noise.

fault diagnosis; soft threshold; spiking neural network (SNN); surrogate gradient method

湖南省自然科学基金（2022JJ50088、2023JJ50198）

2023-10-08

2023-11-27

李 浩（1998—），男，安徽省合肥市人，硕士研究生，主要从事基于深度学习的轴承故障诊断方面的研究工作。