基于融合集成算法的配电网负荷预测研究
2024-03-14吴金淦谭守标
李 强,赵 峰,吴金淦,谭守标
(1.国网信息通信产业集团有限公司,北京 102200;2.安徽继远软件有限公司,安徽 合肥 230088;3.安徽大学集成电路学院,安徽 合肥 230601)
0 引言
配电网中的负荷预测能够有效保障电力运行状态的稳定,是配电网健康评估的重要指标。随着电网的不断转型与升级,电力负荷预测的精度要求也越来越高。因此,负荷预测的研究一直在不断深入。有效的配电网负荷预测可以减少电力资源的浪费、降低运行维护的成本,为绿色电网的转型提供条件[1]。传统的电力负荷预测经过不断的探索和研究,已形成诸多成果,预测的效果也不断提高。但随着人们的物质条件的不断丰富,空调、热水器等耗电较大的电器需求量日益激增,逐年刷新了电力负荷峰值。电力负荷具有较大的波动性,使电力负荷预测的难度和复杂性有了很大提高。这对传统的负荷预测技术提出了新的要求。众多学者也在不断研究新的预测技术和方法。
传统的电力负荷预测方法众多,由早期的时间序列和回归分析的基本方法到人工智能机器学习算法在电力负荷预测上的应用,使得负荷预测的体系不断成熟[2]。机器学习算法预测电力负荷的典型代表有支持向量机(support vector machines,SVM)、神经网络、随机森林等算法[3]。这些算法在不断的改进和优化中逐渐提高了预测的准确率。文献[4]对于负荷的预测主要使用遗传算法(gentric algorthm,GA)优化模型参数,但参数优化的工作量较大、时间消耗较多。文献[5]在XGBoost算法预测负荷的基础上提出使用贝叶斯算法进一步优化模型,以提高短期负荷预测的效果。以上研究均采用单一算法进行负荷预测。对于复杂、随机变化的负荷量而言,单一算法预测的效果不理想。即使对单一算法进行优化,预测的精度变化也较小、适应性较差。
本文将相关特征选择与优化Stacking集成学习算法相结合,提出了一种基于融合集成算法的配电网负荷预测模型。本文在数据集的选择上,综合相关系数和灰色关联算法对样本中负荷影响较小的特征进行剔除,留下相关性高的样本作为模型的训练输入。同时,本文对传统Stacking集成学习的输入和输出特征进行优化,提高了模型的预测效果。所提模型比单一算法模型的预测具有更高的准确率,以及更强的稳定性和健壮性。
1 算法理论概述
1.1 特征因素分析方法
1.1.1 相关系数法
相关系数是衡量样本特征与负荷变化的关联性强弱的一种分析法[6]。一般而言,相关系数的计算方法主要分为两种,分别是Pearson系数法和Spearman系数法[7]。因为本文电力负荷预测主要是衡量各样本特征与负荷的线性关联程度,而Spearman系数主要是衡量变量之前的单调关系,所以本文选用Pearson系数分析更为适合。各样本特征与负荷的线性相关程度P为:
(1)
P在(-1,1)内取值。|P|越接近1,表明样本特征与负荷变化量关联性越强;越接近0,则表明关联性越弱。
1.1.2 灰色关联算法
灰色关联算法可以计算出样本各特征与负荷变化的数值关系,通过数值可以衡量两种数值的相关程度[8]。灰色关联算法对于特征样本的数量要求较低,在小样本下也能够表现优异的关联性。因此,灰色关联算法可以较好地衡量样本特征与负荷变化之间的关系。灰色关联算法的一般步骤如下。
①母序列和子序列确定。本文的母序列即参考序列为负荷的变化量L=L(k)(k=1,2,…,n);子序列即比较序列为各样本特征量Fj=Fj(k)(k=1,2,…,n,j=1,2,…,m)。其中:L(k)为不同维度的负荷变化量;j为样本特征量的个数;k为测试样本的个数。
②规范化处理。规范化处理又称无量纲处理,是必要的步骤。系统中不能直接比较或者难以比较的数据,可以在一定的规范化处理后进行比较。本文可采用初值化处理法。其计算式为:
(2)
③特征差序列值求取。
Δi(k)=|L(k)-Fi(K)|(k=1,2,…,n,i=0,1,…,m)
(3)
式中:Δi(k)为不同维度样本特征差值序列值。
④计算样本特征序列和负荷变化量之间的关联系数δi(k)。
(4)
式中:ρ为关联分辨系数,取值在(0,1)之间,ρ越小则分辨率越大。
当ρ≤0.55时,分辨率表现较好。本文选取ρ=0.5作为分辨系数以进行计算。
⑤关联度大小计算。
(5)
式中:ri为样本特征关联度值。
1.2 融合集成算法
Stacking集成算法是一种分阶段预测算法,具有较高的可扩展性,能够充分利用样本数据集进行多层训练,以提高算法的精度[9]。Stacking集成算法一般包括两个阶段。一阶模型即初级模型,由多个机器学习算法组成。为了减少初级模型的过拟合,此阶段采用交叉验证的方式对输入原始样本进行训练,并将得到的输出结果规范化后作为二阶模型的输入,以得到识别结果。Stacking集成算法的预测结构如图1所示。
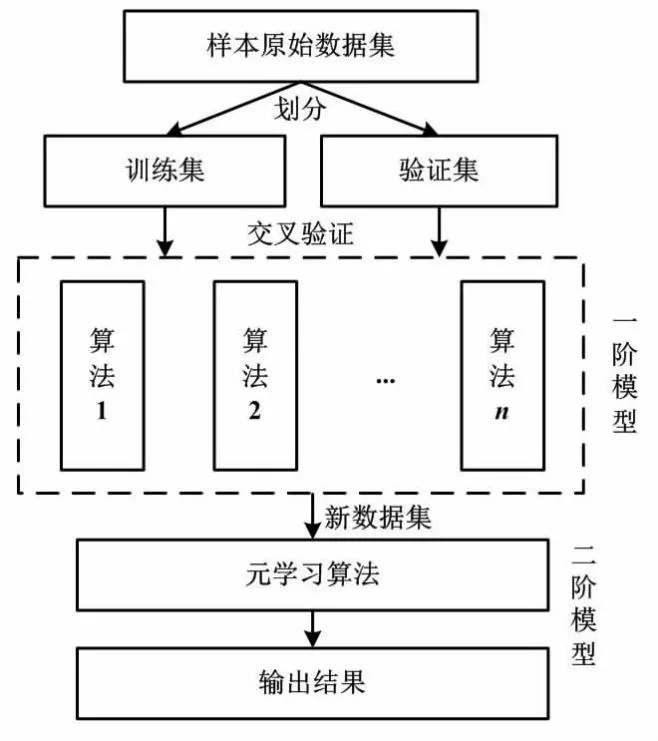
图1 Stacking集成算法的预测结构
2 融合集成算法的负荷预测研究
2.1 融合集成算法的组合原则
Stacking集成算法的使用需要考虑一阶模型各初级算法的选择以及二阶模型中元学习算法的选择。本文的初级算法选择主要依据如下。
①尽可能选择算法之间原理差异较大的模型进行组合。所产生的结果相关性较低,对于结果的预测效果有很好的提升。
②选择单个算法预测效果好、性能较强的模型进行组合,以提高模型输出特征数据的有效性。
常见的机器学习算法中原理差异较大的算法包括XGBoost、长短时记忆(long short-term memory,LSTM)、灰狼优化-反向传播(grey wolf optimization-back propagation,GWO-BP)和SVM这4种。但对于Stacking集成算法,并不是选择越多的算法进行组合预测效果越好,而是要在预测效果优异的前提下兼顾时间效率,从而提升模型整体的性能和效率。
2.2 融合集成算法的优化
传统的集成算法将训练数据分为K等份,取1份作为验证子集,余下(K-1)份为训练子集,采用交叉验证法进行模型的训练,并取各初级算法预测结果的均值作为元学习算法的输入特征[10]。这就存在数据划分不均导致的预测结果不佳的情况。因此,本文对初级算法和元学习算法的输入样本分别作以下改进。
①初级算法的改进。依据初级算法的个数将归一化后的特征样本进行拷贝,并结合样本采样比例进行n次随机不放回抽样,产生(n-1)个训练子集和1个测试子集以对初级算法进行训练;同时,依据验证集的预测值与真实值的误差,给每个初级算法分配权重。权重越大,则误差越小。
②对元学习算法的输入结果进行优化,依据初级算法的预测精度对预测结果进行加权平均计算。所得结果作为元学习算法的输入,可以提升模型的预测效果。
2.3 融合集成算法的实现流程
融合集成算法的一般流程如下。
①获取初始样本特征集,通过相关系数和灰色关联算法对样本中负荷影响较小的特征进行剔除和整合,形成初级样本数据集D1。
②对样本数据进行规划化和归一化。
③通过2.2节改进的初级算法,得到(n-1)个训练子集和1个验证子集。
④将训练子集放入初级算法中进行训练,并使用验证子集对初级算法的预测结果进行验证;同时,依据验证集的预测值与真实值的误差,给每个初级算法分配权重W。
⑤依据初级算法的预测精度对预测结果进行加权平均计算,并将所得结果作为元学习算法的输入特征。
⑥将结果输入元学习算法中,得到预测的结果。
3 试验和结果
3.1 数据集获取与评价
试验采用安徽省10 kV配电网某线路32个台区2018~2020年的历史数据[11](包括电力负荷、温度、湿度、雨量、风力、假日、月度、季节数据)。其中,数据采集间隔为1 h。本文以2018~2019这2年的历史数据组成数据集,建立预测模型对2020年数据集进行预测,并比对与2020年真实数据之间的差异。相关模型运行在Intel Core(TM)i7 3.6 GHz、16 GB内存的计算机端。操作系统为Windows10。预测软件为Matlab。模型预测结果主要采取准确率、平均绝对百分比误差(mean absolute percentage error,MAPE)和均方根误差(root mean square error,RMSE)作为评价指标。
(6)
式中:Ia为准确率;TP为预测值与实际值均为正;TN为预测值与实际值均为负;FP为预测值为正、实际值为负;FN为预测值为负、实际值为正。
(7)

(8)
式中:Ir为RMSE值。
3.2 集成学习算法的选择与确定
集成算法模型中元学习算法的确定不仅需要保证预测结果的准确率,还应兼顾时间效率。只有这样才能实现模型的活化性和可扩展性。因此,本文选择初级算法中的3个进行组合,以形成一阶模型。以下对各初级学习算法进行验证,以选择评价结果较好的算法作为本文集成学习算法。
为了保证算法选取的高效和工作量的适度,本文选择和确定的集成算法的训练、测试样本数量不宜过大。为了保证数据的幅度变化,需在本文大量样本中采用间隔样本剔除的方法,即将1 d的24条数据间隔剔除,形成12条数据。数据集任意选取1周的84条负荷数据并将其中1 d的12条数据作为验证集、其余数据作为训练集,以统计XGBoost、LSTM、GWO-BP、SVM这4种算法的预测误差。误差较小模型的预测结果较好。各算法的参数设置如下。
①XGBoost算法。试验设置算法的学习率为0.12、子集观察值的最小权重和为1、树的最大深度为5、样本特征的采样率为0.8、alpha正则化值为0、最小损失函数减少值为0.2。
②LSTM算法。试验设置算法学习率为0.09、算法的神经元个数为56个、全连接层的神经元个数为32个、激活函数为R函数。
③GWO-BP算法。由于反向传播(back propagation,BP)神经网络易陷入局部最优,而灰狼优化(grey wolf optimization,GWO)算法的灰狼寻优能够提升全局的搜索性能,试验使用GWO优化BP神经网络,以提高算法的稳定性。试验设置狼群数为120、最大迭代次数为80、神经网络的输入层和隐含层分别为4和3、输出节点为1、激活函数为S函数。
④SVM算法。对比线性核函数,其惩罚系数c为10。
不同算法预测负荷结果误差对比如表1所示。

表1 不同算法预测负荷结果误差对比
由表1可知,XGBoost算法的预测MAPE和RMSE均较小,表明该算法的预测准确性高。这是由于该算法自身对损失函数进行优化,使用一阶、二阶导数进行迭代,对预测负荷变化值的依赖性表现效果好。GWO-BP算法经过优化,预测效果明显优于LSTM算法,而预测误差仅次于XGBoost算法。LSTM算法由于其特殊的记忆结构,在提取关联特征上表现优异,且误差的结果也比较理想。SVM算法的应用较广,主要应用于非线性样本,对于负荷预测的效果不如其他算法。
因此,本文的集成学习一阶模型的初级算法选用XGBoost算法、GWO-BP算法、LSTM算法,二阶模型的元学习算法选用XGBoost算法。这就组成了Stacking集成学习基本模型。
3.3 特征选择
数据集确定后,需要对数据集进行规范化,以形成初始数据集。数据集中包括历史负荷、温度、湿度、雨量、风力、假日、月度、季节这8类数据。相关系数法对于试验环境及样本数量均有很高要求。因此,本文加入不依赖于样本特征量的灰色关联度算法对变量关系进行综合评估,以使相关性计算更为可靠。通过相关系数和灰色关联算法对样本中的8类数据进行相关性计算。关联度R为:
(9)
式中:r0为灰色关联度;|r1|为相关系数的绝对值。
本文将R>0.8的数据作为有效样本,除去关联度小的特征数据,以组成特征集。
试验对本文的8类数据分别进行关联度计算。季节、历史负荷、月度、温度以及假日这5类数据的关联度结果分别为0.965、0.932、0.922、0.907、0.896。这说明这些因素与负荷变化强相关。而湿度、雨量、风力这3类数据的关联度结果分别为0.681、0.413、0.242,对负荷的变化影响小。因此,本文选择季节、历史负荷、月度、温度和假日这5个强关联特征数据作为初始数据集,以进行训练和验证。
3.4 融合集成算法的性能验证
3.4.1 误差分析
本文融合集成算法主要采用了XGBoost算法、GWO-BP算法、LSTM算法作为初级算法,XGBoost算法作为元学习算法。为了验证融合集成算法模型的预测效果和时间效率,本文融合集成算法与Stacking集成算法[12]、XGBoost算法、GWO-BP算法进行了比较分析。Stacking集成算法包括XGBoost、LSTM、SVM和k近邻(k-nearest neighbour,KNN)。不同算法预测负荷结果的误差对比如表2所示。
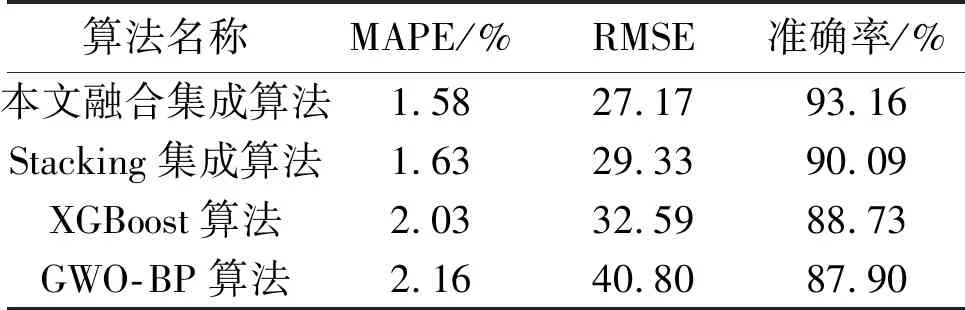
表2 不同算法预测负荷结果的误差对比
由表2可知,Stacking集成算法主要组合了多个预测能力良好的算法,在预测中取长补短,使得模型更好地减少了过拟合,提升了模型的扩展性和稳定性,以及预测效果。Stacking集成算法中对算法的选择也影响了预测的精度。组合算法一般选用单一算法效果较好且预测原理差异较大的算法,本文选取了3个组合算法。相较于Stacking集成算法,本文融合集成算法的预测效果较好:MAPE减少了0.05%;准确率提升了3.07%;RMSE减小了2.16。该结果说明了本文融合集成算法具有较好的预测结果,对于负荷的预测效果提升显著。不同算法的负荷预测对比如图2所示。
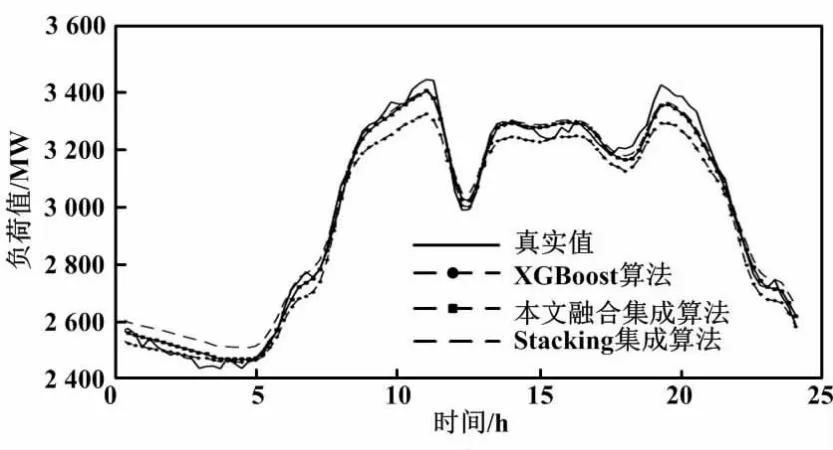
图2 不同算法的负荷预测对比
3.4.2 训练时间分析
Stacking集成算法组合了多种算法,虽然预测精度较高,但是时间消耗较大。这也是集成算法的缺点。本文的融合集成算法选用3个初级算法组合,从而在一定程度上降低模型训练和测试时间的消耗。同理,本文将本文融合集成算法与Stacking集成算法、XGBoost算法、GWO-BP算法的训练和测试时间进行比对分析。不同预测算法的时间对比结果如表3所示。
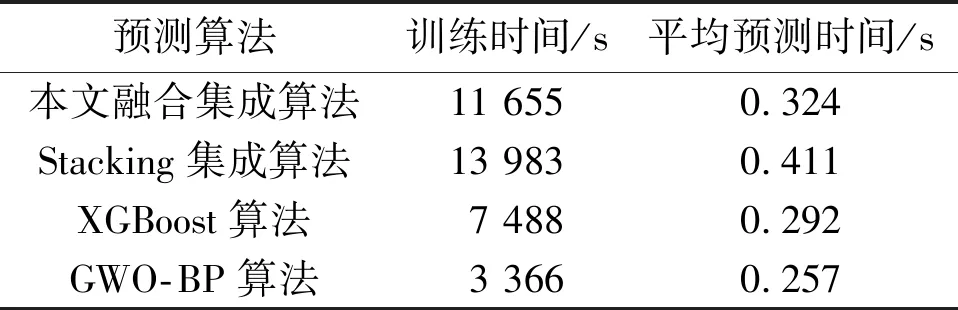
表3 不同预测算法的时间对比结果
由表3可知,集成算法的训练时间相比较单一算法有了一定的增加。这是因为集成算法组合了多种初级算法,增加了算法的复杂度。除了训练时间增加明显外,模型的预测时间相差较小、检测效率也较高。本文融合集成算法由于组合算法的个数少于Stacking集成算法,因此在训练时间上表现优异。其检测时间也比Stacking集成算法减少了0.087 s,与其中最快的单一算法GWO-BP的预测时间相差0.067 s,小于0.1 s。该结果说明本文的融合集成算法的时间效率有所提升。
4 结论
负荷预测作为电力工作中必不可少的环节,对电力的稳定运行和可靠性评估有着重要意义。机器学习算法的不断研究和发展也为算法的改进提供了参考。为了提升预测效率,研究的重点逐渐转移到了融合算法上,即将多个单一算法组合以发挥出各自算法的优势。这减少了单一算法的过拟合,在研究中表现出了良好的效果。
本文通过对融合集成算法进行研究,提出了一种基于关联特征选择的融合集成算法。该研究的主要贡献在于两个方面:一是对于初始数据集选取,采用相关系数和灰色关联算法综合分析样本中的关联性,提取关联性高的样本数据集,不仅缩短了试验的训练时间还提高了算法的预测精度;二是对传统Stacking集成学习的输入和输出特征进行优化和改进,进一步提高了模型的预测效果。试验结果表明,基于融合智能算法嵌入集成的配电网负荷预测模型与其他Stacking集成学习算法、XGBoost算法、GWO-BP算法、SVM算法等相比,负荷预测的精度提升了3.07%、预测时间效率较高、总体性能表现较好。该模型在配电网的负荷预测中发挥了重要作用。
