基于完全邻域保持嵌入的光伏组件热斑故障诊断

宋远大,易 辉+,缪小冬,冒泽慧,李红涛

(1.南京工业大学 电气工程与控制科学学院,江苏 南京 211816;2.南京航空航天大学 自动化学院,江苏 南京 210016;3.中国电力科学研究院有限公司,江苏 南京 210003)

0 引言

随着环境问题的不断加剧,传统能源在世界能源的供应占比逐渐下降,光伏发电业务快速发展,并凭借其安全性和可靠性成为学界研究焦点[1-2]。光伏组件是光伏发电的基本组成部分,其工作环境恶劣,容易被树叶、鸟粪等遮挡,被遮挡的电池单元变为负载并释放热量,经过一定时间累积,易使光伏组件形成热斑故障[3]。

DHIMISH等[4]采用热成像仪拍摄局部阴影遮挡下的光伏组件,同时测量其I-V曲线并进行评估,分析热斑效应发生前后输出功率性能的差异,然而使用该方法成本高昂;SPANOCHE等[5]建立了光伏组件模型,将光伏组件工作时的电压、电流、温度等参数与标准情况下的光伏组件进行对比,从而判断光伏组件的工作状态;KUEIHSIANG等[6]在光伏组件串的特定位置安装电流传感器,检测电流值并与正常工作下的光伏组件串对比,从而定位故障,然而该方法无法精准判断多发生的故障是否为热斑故障;DU等[7]采用数种机器学习算法诊断支路异常情况,同时利用简易模型提升了诊断精度。以上方法主要通过图像处理与光伏组件建模对组件故障进行诊断。

目前,主流方法是数据驱动式[8]的光伏组件热斑故障诊断,该方法通过挖掘光伏组件特征参数之间的内在联系来诊断热斑故障。例如ROUANI等[9]采集电流、电压和功率3个特征参数,用主成分分析(Principal Component Analysis, PCA)算法识别不同类型阴影遮挡引起的热斑故障,诊断结果良好,但样本复杂性不足;HONGTIAN等[10]采集光伏组件的8个特征参数,用邻域保持嵌入(Neighborhood Preserving Embedding,NPE)算法识别不同区域不同面积的阴影遮挡引起的热斑故障,然而NPE算法经常遇到特征矩阵的奇异性问题,很难应用于高阶矩阵。

综合以上热斑故障诊断方法出现的问题,本文实际采集15块光伏组件在不同位置与不同面积阴影遮挡下的8个重要特征参数,采用基于完全邻域保持嵌入(Complete Neighborhood Preserving Embedding,CNPE)算法对样本数据进行特征提取,随后建立评估模型,并提出一种评估函数进行光伏热斑故障诊断。

1 背景知识

1.1 热斑故障

光伏组件可以将太阳能转化为电能,但因其工作环境通常比较恶劣而容易发生故障,常见的故障有短路故障[11]、开路故障[12]、接地故障[13]、失配故障[14]和热斑故障[15],其中阴影遮挡引起的热斑故障不可忽视。光伏组件由若干个电池单元串联组成,每串电池单元并联一个旁路二极管,发生热斑故障时,热斑所在电池串的旁路二极管两端形成正向偏压,使故障所在电池串停止工作,其他正常电池串继续发电。

旁路二极管虽然可以有效缓解光伏组件的热斑故障,但是热斑故障造成的影响仍然存在,而且与生效的旁路二极管并联的电池串失效,将降低光伏组件的发电效率。

光伏组件的等效电路如图1所示,其中T为温度,Ir为辐照度,I1,I2,In为各电池串产生的电流,Ipv为组件电流,当组件中的电池单元被阴影遮挡时,I1≈I2>In,Ipv>I1,被遮挡的电池单元成为负载,持续释放热量,若该处长时间未被发现,则会形成局部高温,严重时将烧毁光伏组件,引发火灾。

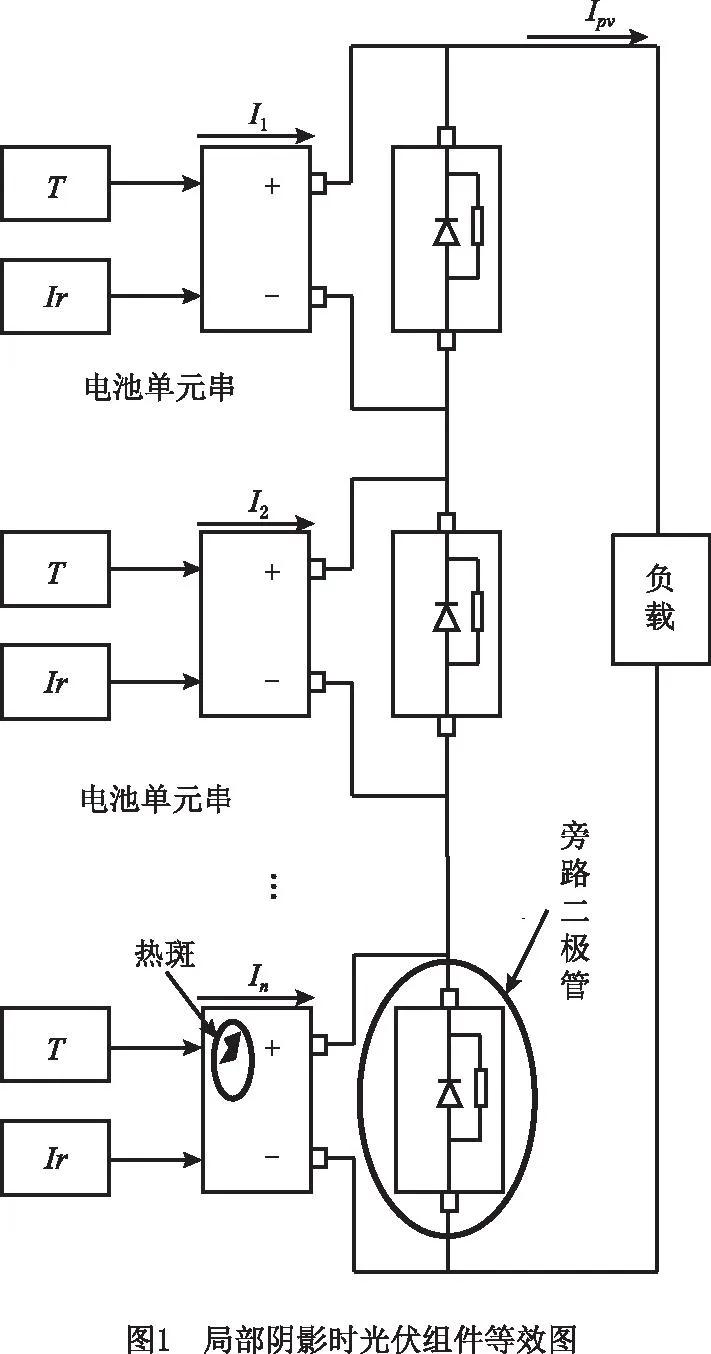
1.2 邻域保持嵌入

NPE算法是当下应用广泛的流形学习算法之一[16],其可以通过一组线性投影矩阵将高维流形的局部邻域结构在欧式空间内重构至低维子流形。NPE算法步骤如下:

(1)利用K最近邻法为每个数据点构造邻接图。

(2)最小化代价函数ε(W),获得权重矩阵W:

(1)

式中:xi,xj为特征提取前的任意数据点;N为整个数据集;wij为xi和xj之间的关系矩阵并满足

(2)

式中knn(xi)为xj的近邻集合。

(3)计算投影矩阵。

特征提取前的数据点xi在特征提取后的低维特征空间中表示为yi,且yi=ATxi,计算降维后的代价函数式需最小化式(3)。

(3)

将yi=ATxi带入式(3),得到

φ(Y)=ATX(I-W)T(I-W)XTA。

(4)

令M=(I-W)T(I-W),其中I为单位矩阵,最小化问题转换为如下形式:

s.t.

AXXTA=c。

(5)

式中c为正常数。投影矩阵A的列向量最终由下列特征值问题解出:

XMXTA=λXXTA。

(6)

特征矩阵XMXT和XXT均为方阵,在数据驱动的光伏热斑故障诊断中,特征矩阵的维度通常很高,计算广义特征值比较困难。为解决该问题,通常采用PCA或奇异值分解(Singular Value Decomposition, SVD)[17]进行预处理。然而,这两种方法都有明显的缺点。首先,预处理过程可能无法保留样本的重要特征,其次PCA的目标是保留总方差,而NPE算法的目标是保持局部邻域结构,因此采用PCA进行预处理可能无法很好地保留数据特征。

2 基于CNPE的特征提取以及热斑故障的评估函数

2.1 完全邻域保持嵌入

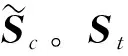
St=X(I-W)T(I-W)XT+XXT。

(7)

对St进行特征值分解:

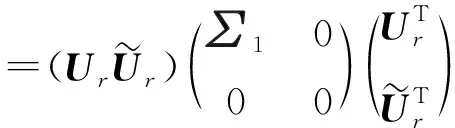
(8)

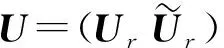
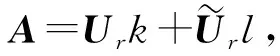
(9)

将目标函数作如下变换:

s.t.

(10)

(11)

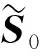
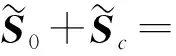
(12)

CNPE算法的目标函数为:

(13)

投影矩阵A的列向量最终由下列特征值问题解出:

(14)

最终,将NPE的广义特征值最小化计算困难的问题转化为式(14)的最大特征值求解问题,而且CNPE的特征值计算精度高,可以有效避免高阶矩阵的奇异性问题。取式(14)解的前t个最大非零特征值ξ1∶ξt,各特征值对应的特征向量为a1∶at,从而得出投影矩阵A,数据投影结果为

Y=(a1,a2,…,at)TX。

(15)

2.2 基于CNPE的特征提取

采集包含光伏组件8个重要特征参数的N个样本为X=[x1,…,xi,…,xN]T,其中xi=[v1(i),v2(i),…,v8(i)]T,v1～v8的定义如表1所示。

表1 光伏组件的重要参数

为了提取数据集X中的非线性特征,需要确定有关时间序列的投影关系,投影前与投影后的数据如下:

(16)

根据式(15)得到投影关系

Yi,s=ATXi,s。

(17)

式中:Xi,s∈Rs×m,Yi,s∈Rs×l,A∈Rm×l,s为整数。式(17)将光伏组件的高维信息投影至低维空间,会丢失一定信息量,因此产生重构误差,重构误差难以避免且仅与系统不确定性有关。重构误差矩阵Ei,s推导如下:

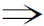
(18)

式(17)给出的投影在光伏组件热斑故障诊断方面有如下优点:①削弱光伏组件中随机不确定性造成的负面影响;②在空间角度评估重构误差,使结果更加可靠。

2.3 热斑故障的评估函数

定义发生热斑故障时获取到的光伏组件数据集为

Xf=X+F。

(19)

式中F为由热斑故障引起的异常矩阵,F∈RN×m。式(17)同样适用于故障数据集,故障数据集投影到低维空间为

(20)

(21)

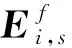
(22)

式中tr为矩阵的迹。选取光伏组件正常工作下评估函数的最大值作为阈值,即

Jth=maxJ(i)。

(23)

当光伏组件出现热斑故障时,式(18)改写为

(24)

判断光伏组件是否发生热斑:

(25)

3 实验

3.1 实验平台和实验设备

本文实验地点为国家电网电力科学研究院实验验证中心,所用光伏组件规格统一,均为两栅多晶,边框厚度4 mm,如图2所示。实验数据采集设备为AV6592便携式太阳能测试仪,如图3所示。

便携式太阳能测试仪与辐照度计共测得光伏组件的8个参数,如表1所示,本文模仿实际应用中光伏组件易出现的阴影遮挡情况,将不同大小的纸板、透明胶带和电线依次放置在同一块光伏组件的不同位置上,共有15种阴影遮挡情况(如图4),包括单故障和多故障,每一种情况都基于相同规格的光伏组件进行模拟。

分别用纸板遮挡模仿实际光伏组件应用中不同面积、不同位置遮挡的单故障情况和多故障情况;情况1～情况4为面积相同、位置不同的多故障状态;情况5～情况8为不同位置的小型遮挡;情况9和情况10为用纸板遮挡模仿现实中跨电池单元的遮挡;情况11为用纸板遮挡模仿现实中不规则跨多个电池单元的遮挡;情况12和情况13为不同位置下的单故障遮挡;情况14为用透明胶带遮挡模仿实际应用中的乌云遮挡;情况15为用电线遮挡模仿实际应用中的线性遮挡。

3.2 实验结果

图5所示为光伏组件正常工况下的评估函数曲线,其中横坐标为0～100,每个点位对应一个评估函数值J。取光伏组件正常工况下的最大评估函数值作为诊断阈值,即图中虚线。图6和图7所示为情况1～情况8的诊断结果,可见本文方法均准确诊断出组件处于异常状态,且遮挡面积与评估函数值正相关。

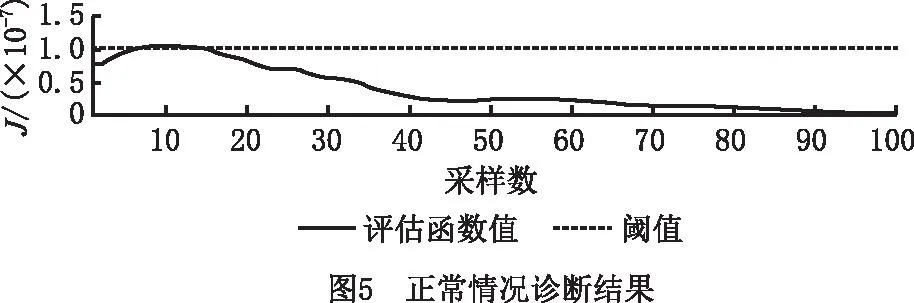
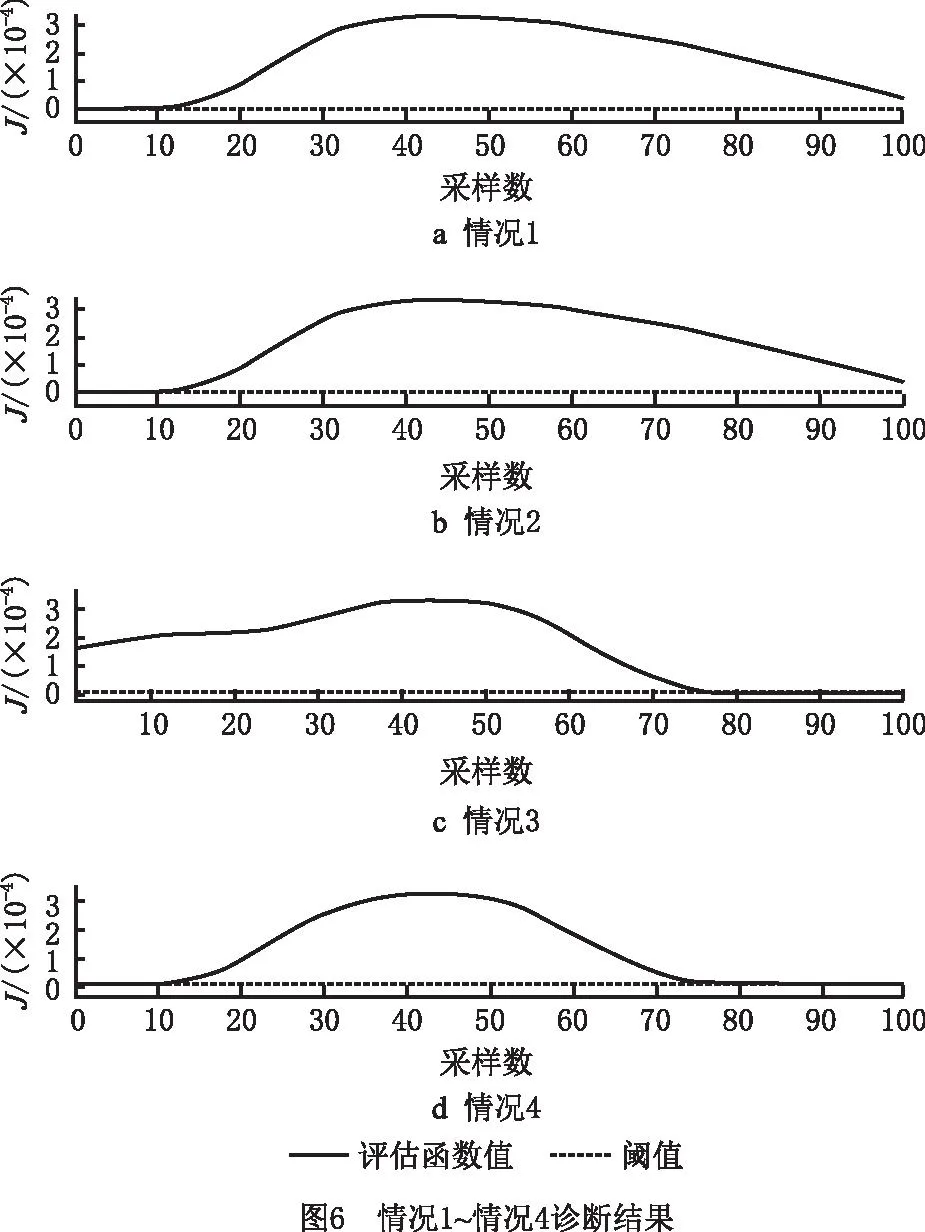
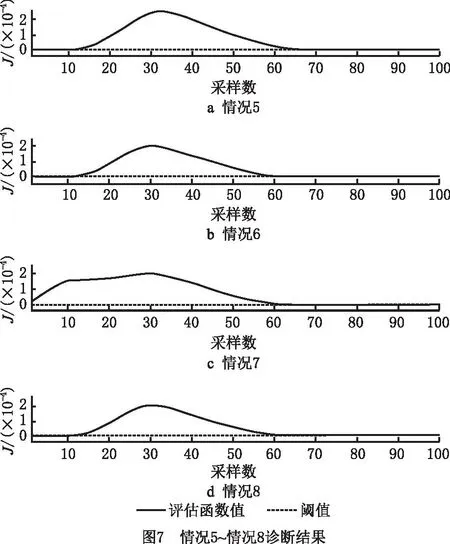
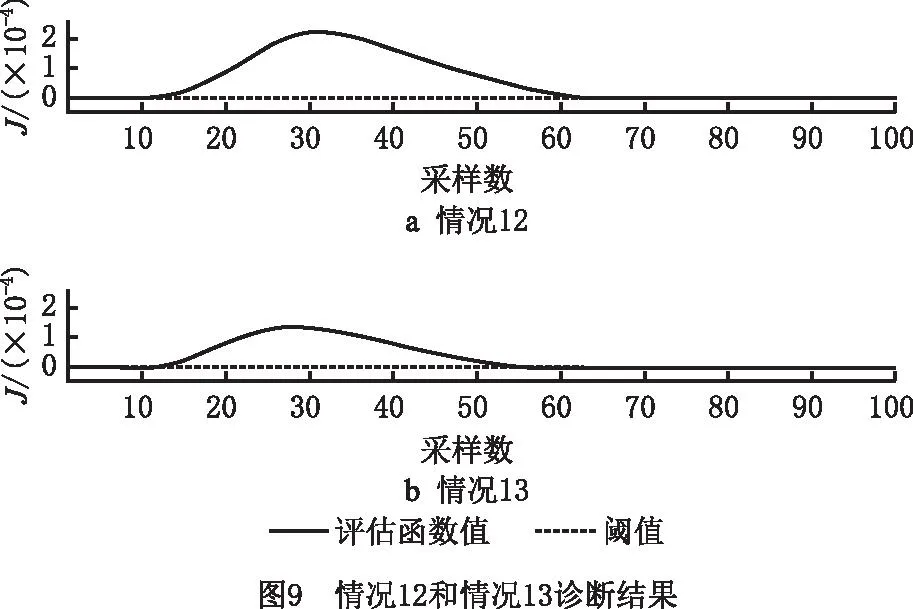
图8所示为3种大面积跨电池单元串的遮挡,图9所示为两种单故障小面积遮挡,图10所示为两种微小遮挡。由上述实验得出结论,基于CNPE的特征提取和空对空投影的故障诊断方法可以准确判断光伏组件是否发生热斑故障,而且由评估函数值可以判断光伏组件热斑故障的严重程度,评估函数值与阴影遮挡面积正相关。

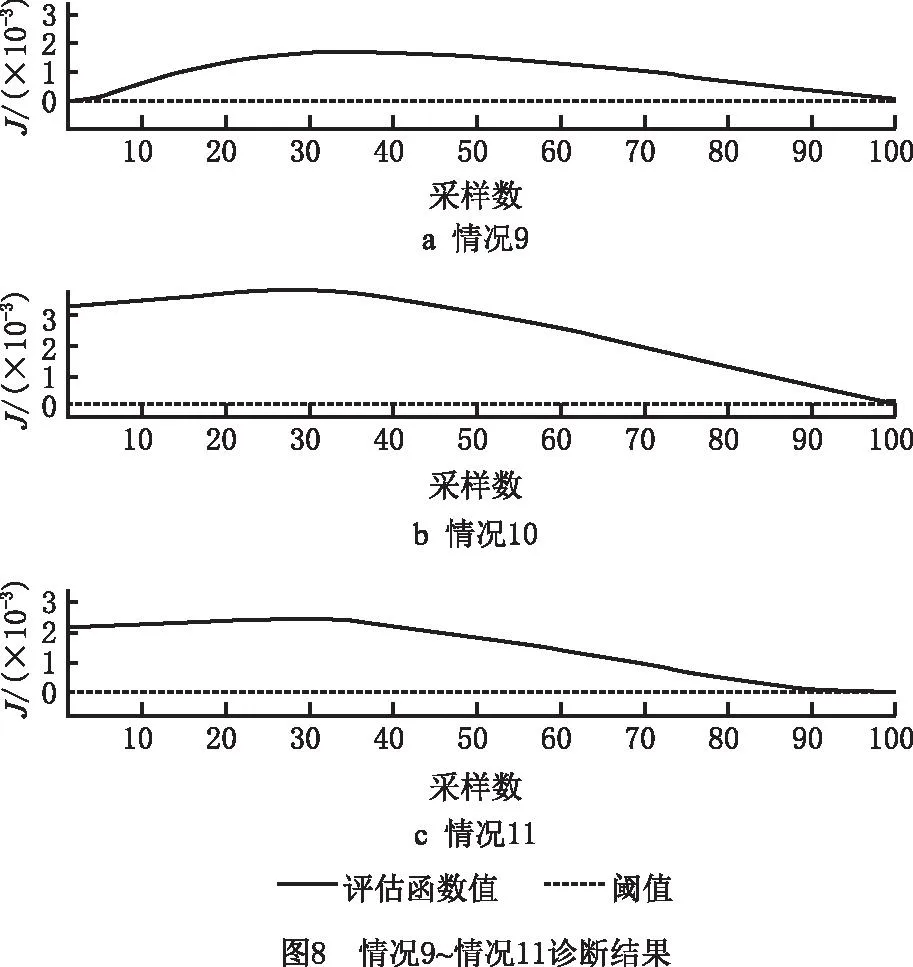
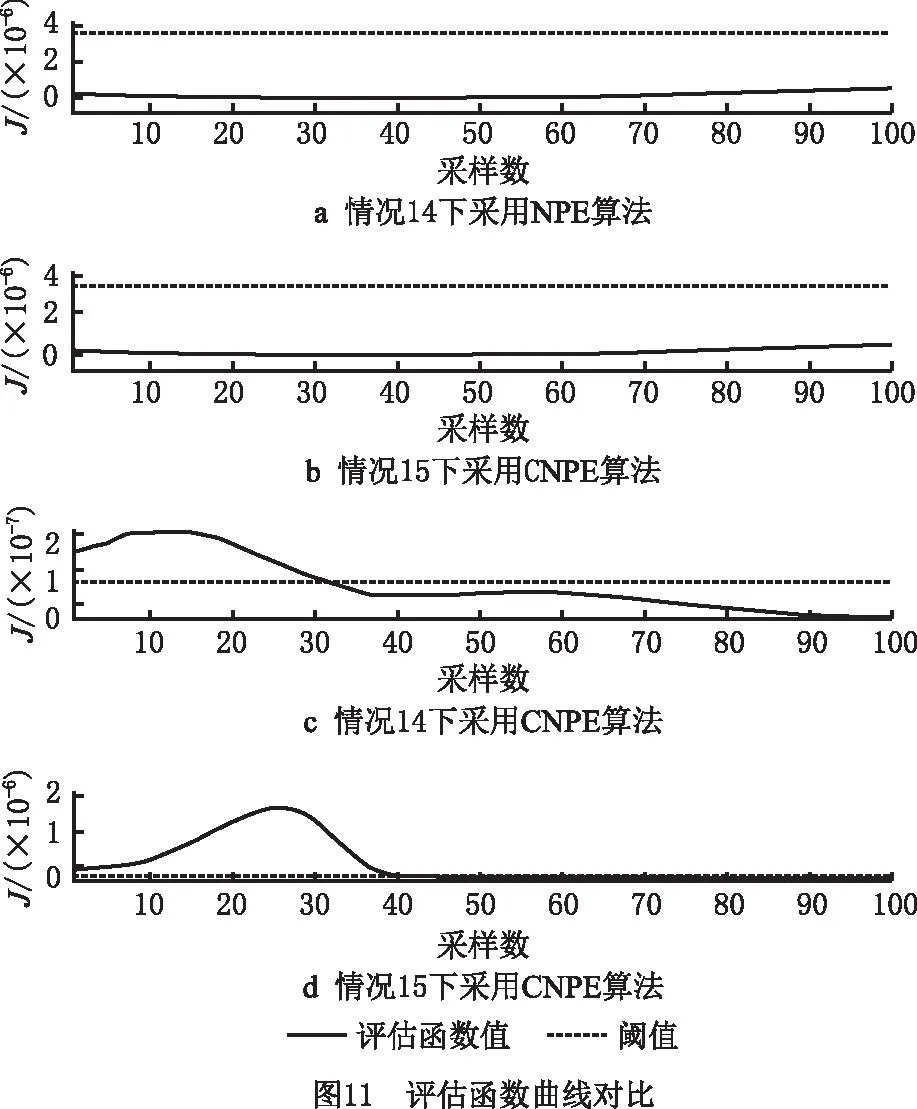
相比NPE算法,本文方法的优点在于可以检测出细小阴影遮挡引起的热斑。例如图10中的情况14和情况15分别为透明胶带遮挡与电线遮挡,采用NPE算法未诊断出热斑故障,而采用本文方法则可诊断出故障。如图11所示,采用NPE算法时,情况14和情况15的评估函数曲线均低于阈值,未能诊断出轻微热斑故障,而CNPE算法的评估函数值均高于阈值,能够成功诊断出轻微热斑故障。

15组实验的结果如表2所示,情况1～情况4中,情况1的遮挡面积较大,由NUM值判定为严重程度故障;情况2遮挡面积小于情况1,因此NUM也小于情况1,根据评价等级被判定为一般故障;情况3和情况4的遮挡位置不同,但遮挡面积相近,因此NUM值相近,根据评价等级判定为严重故障;情况5～情况8的遮挡位置不同,但遮挡面积相近,根据评价等级均判定为一般故障;情况9～情况11的遮挡面积大,根据评价等级判定为严重故障;情况14和情况15分别为透明胶带遮挡与电线遮挡,遮挡面积小,因此根据评价等级划分为轻微故障。

表2 严重程度判定

为了验证本文所提方法的优越性,选取具有代表性的几种特征提取算法进行对比,分别为NPE、PCA和等距特征映射(Isometric Mapping,ISOMAP)。

将上述几种对比算法分别运行60次,记录各算法的运行时间,并将其绘制为箱线图,如图12所示。可见,采用CNPE算法进行热斑故障诊断时,诊断时间远低于NPE和ISOMAP,略低于PCA。取各算法箱线图的中位数和各算法的识别率进行对比,如表3所示。

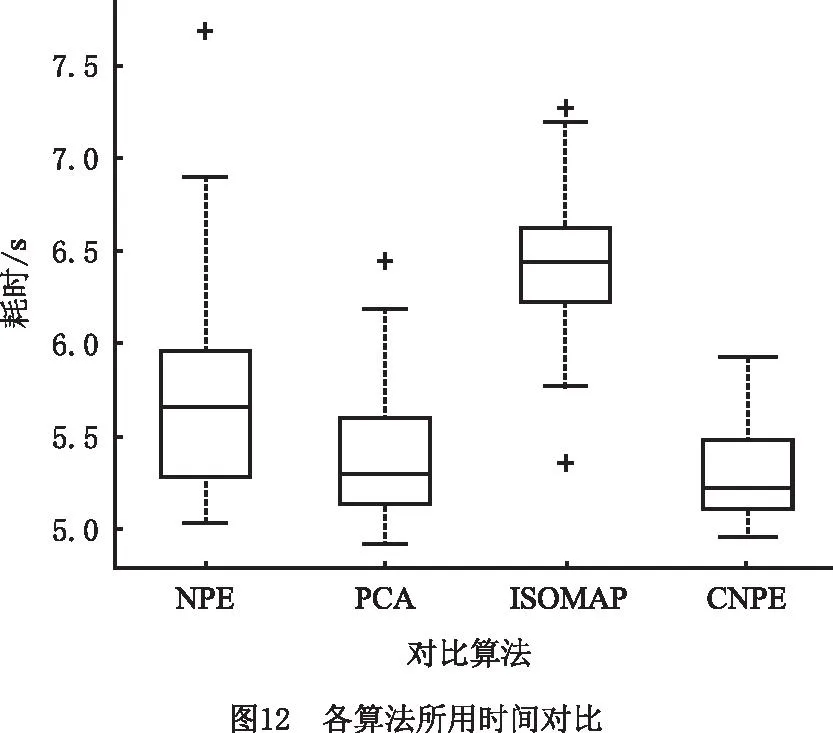
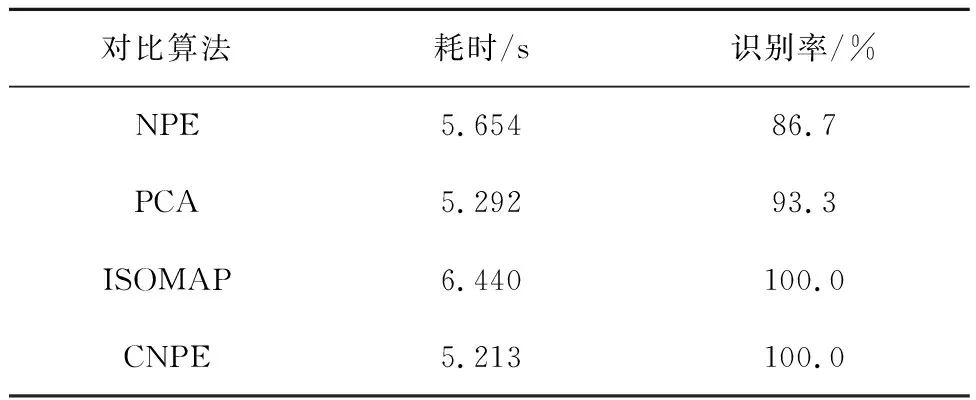
表3 算法性能对比

基于CNPE的热斑诊断方法在运算速度和识别率上均优于采用NPE和采用PCA的热斑故障诊断方法,而ISOMAP的算法识别率与CNPE算法相同,但耗时大于CNPE算法。

根据以上实验结果及第2章的理论分析,得出以下结论:

(1)阴影遮挡引起的热斑故障与本文所提评估函数值正相关,即热斑故障越严重,评估函数值越高。因此,实际应用中若出现较高的评估函数值,相关人员则应立即对该光伏组件进行故障排查。

(2)在热斑故障发生初期,本文方法已具有良好的诊断能力,后续研究可以通过观察关键参数之间的相关性来提高诊断能力并估算阴影遮挡的面积。

4 结束语

光伏组件热斑故障诊断传统方案多基于红外图像实现,近期基于组件运行数据挖掘的智能诊断方法因成本低廉、维护方便,正成为一个新的方向。采用数据驱动式的方法进行光伏组件热斑故障诊断的核心问题在于如何从运行数据中挖掘有效特征,并通过特征为运行状态建立精准的监测模型。本文提出一种CNPE诊断方法,该方法首先采用CNPE对冗余度高的故障信息进行特征提取;其次降低数据维度并获取主要相关特征;然后根据降维前后产生的重构误差矩阵建立热斑评估模型,该模型确立了热斑故障严重程度的四级评价指标;最后,通过国家电网电力科学院实验平台完成15组热斑诊断实验与对比实验,取得了良好的效果。