考虑轴颈倾斜与空泡运动的径向滑动轴承油气润滑分析
2024-03-13田天赐房立庆师素双张浩师占群
田天赐,房立庆,师素双,张浩,师占群
(河北工业大学机械工程学院,天津 300130)
径向滑动轴承由于具有结构简单、工作稳定以及高回转精度等优点被广泛应用于旋转机械设备中。一方面,随着现代机械设备向着高速重载的方向发展,滑动轴承在工作运行中,轴颈与轴瓦形成的楔形间隙会不可避免地混入微小气泡。气泡的存在会影响油膜压力分布,进而影响承载力、摩擦力等润滑特性参数。国内外学者从理论与实验方面探究油气润滑对滑动轴承性能的影响并得出了不同的结论。CHUN[1]利用NIKOLAJSEN[2]推导的两相流黏度、密度模型,将能量方程与雷诺方程耦合求解得出,提高通气量、减小气泡尺寸可提高油膜承载力。然而,GOODWIN等[3]的实验结果表明,在高速工况下,气泡的存在会导致轴承承载能力轻微下降,在偏心率较大时,气泡的存在对承载力的影响很小。JANG和KHONSARI[4]研究了充气油在稳态和动态加载工况下滑动轴承的热流体力学性能,并利用2种模型进行仿真得出:在正常转速下,润滑油中气泡对压力场和温度场的影响较小,而气泡的存在则显著降低了润滑油的密度和有效黏度。王建文和安琦[5]根据弹流润滑理论对油气润滑滚动轴承进行了数值模拟,结果表明,油气润滑能使轴承摩擦力降低25.8%,使承载力提高2%。张绍林等[6]通过实验拟合得到两相流的黏度计算模型,并基于该模型分析了低含气率下圆柱动静压轴承的动静特性。为更准确地揭示油气润滑对滑动轴承的影响,一些学者将考虑空泡运动RP方程(Rayleigh-Plesset)耦合到雷诺方程中。SNYDER等[7]提出一种新的空化模型,将表面膨胀黏度引入到动态生长气泡的界面应力平衡中并得出增大表面膨胀黏度项会带来失稳效应。BRAUN等[8]将能量方程、RP方程与雷诺方程三者耦合,探究了温度、偏心距及换热系数等对压力和空化发展的交错影响。为增加RP方程与雷诺方程耦合求解的数值稳定性,JARAMILLO和BUSCAGLIA[9]开发了一种单步格式算法,结果表明该算法具有良好的收敛性和鲁棒性。
另一方面,滑动轴承由于载荷作用、加工精度及装配误差的影响,轴颈与轴瓦会发生错位。GUHA[10]研究了计入轴颈倾斜与表面粗糙度的滑动轴承的稳态特性,并分析了2种因素对轴承承载力、端泄量、摩擦因数等的影响。NIKOLAKOPOULOS和PAPADOPOULOS[11]在严重磨损工况下建立了摩擦力、倾斜角和磨损深度的解析模型,并针对不同的索默菲尔德数,建立了不对中度与磨损深度的函数。XU等[12]将能量方程与雷诺方程耦合,通过仿真得出在大偏心率和不对中度较大时,紊流对轴承的润滑性能有显著影响。朱少禹[13]分析了轴颈倾斜影响下的粗糙表面径向滑动轴承湍流润滑性能,结果表明:轴承静特性参数随中央截面名义偏心率的增大而增大。
综上所述,国内外学者在不对中轴承的润滑特性分析与油气两相润滑分析方面均取得了很大的研究进展,然而综合分析二者对轴承润滑特性影响的文献较为鲜见。本文作者将完整的RP方程耦合到雷诺方程中,通过Matlab仿真求解油膜压力、承载力、摩擦力和端泄流量等静特性参数,探究油气两相流及轴颈倾斜对径向滑动轴承润滑性能的影响。
1 基本方程与公式
考虑油气两相流润滑的不对中径向滑动轴承的润滑模型如图1所示。
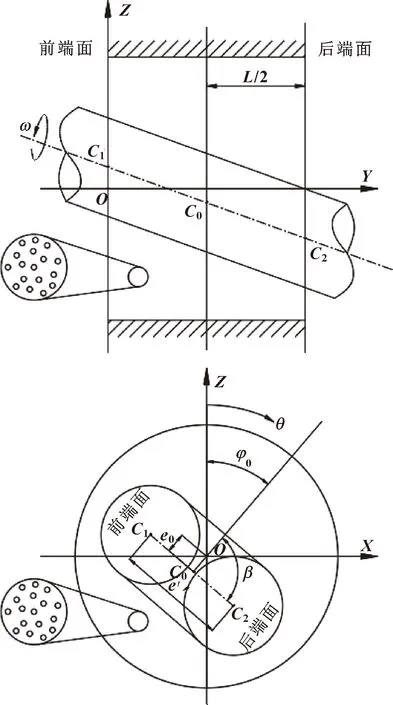
图1 错位状态下径向滑动轴承示意Fig.1 Schematic of radial sliding bearing in dislocation state
当轴承处于层流润滑状态时,轴颈与轴瓦形成的不对中现象会影响油膜厚度从而影响楔形间隙中油膜的压力,进而影响滑动轴承的润滑特性。计入轴颈倾斜影响的油膜厚度公式[14]为
h=c+e0cos(θ-φ0)+tanγ(y-L/2)cos(θ-β-φ0)
(1)
式中:c为油膜间隙;e0和φ0为轴承中央截面上的偏心距和偏位角;β为轴颈中心线在端面处的投影和偏心距矢量的夹角;γ为轴颈中心线与水平线之间的夹角,γ=arctan(e′/L),e′为轴颈中心线在端面的投影距离。
(2)
倾斜程度最大值小于1。
1.1 RPS方程
PLESSET和CHAPMAN[15]在RAYLEIGH提出的理想不可压缩气泡运动模型的基础上引入气泡表面张力和液体黏性,从而形成最早的RP模型解释空泡运动现象,而后一些学者不断完善RP方程。将计入表面膨胀黏度项的RP方程称为RPS方程。以下为包含所有界面性质的空泡动力学方程
(3)
由于RPS方程中惯性项的数值小于压力驱动项和表面膨胀黏度项的0.1%,所以在求解过程中惯性项常被忽略,最终应用于仿真的气泡动力学方程[9]为
(4)
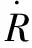
为降低网格精度对数值结果的影响,PIERSON[16]提出一种算法将气泡动力学方程中的R转化为α,修正后的RPS(mRPS)方程为
(5)
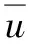
由等温条件下理想气体状态方程及气泡内外压力平衡得
(6)
(7)
式中:pB0为气泡初始压力;patm为标况状态下大气压力。
1.2 雷诺方程
当流动为层流时,瞬态的雷诺方程为
(8)
当润滑剂为油气均匀两相流时,密度ρ和黏度μ可表示为局部含气率α的函数,两相流润滑的混合黏度与混合密度为
ρ=αρB+(1-α)ρL
(9)
μ=αμB+(1-α)μL
(10)
根据质量守恒可得气泡的密度为
(11)
式中:ρB为气泡的密度;ρB0为气泡的初始密度;ρL为润滑油密度;μB为气泡黏度;μL为润滑油黏度。
需要指出,将气泡动力学耦合雷诺方程进行滑动轴承油气润滑分析时,需要做出以下假设:
(1) 含气油液为均匀两相流,润滑油中的气泡沿流线移动;
(2) 由于目前没有简单、实际的非球空穴动力学求解方法,假设微小气泡在压缩和溃灭的过程中始终保持为球形;
(3) 假设轴颈和轴瓦表面传热系数很大,即认为气泡在润滑油中的运动过程是绝热的。
1.3 滑动轴承静特性计算公式
1.3.1 油膜承载力
油膜承载力的水平分力Wx和垂直分力Wy为
(12)
(13)
油膜承载力为
(14)
1.3.2 端泄流量
润滑油从最高压力点向两端流出,润滑油经过两端面流量分别为
沉降监测是进行路基沉降与变形控制的方法,具体的施工流程如下所示:施工准备→观测布点→结构的统计和分析→结果综合分析→判定地层结构的稳定性→地层安全动态分析、提供设计与施工建议书、上报设计与监理单位→反馈设计、施工→是否改变设计、施工方法→新的设计、施工方法。在进行作业的过程中进行数据的检测,科学合理的预测软土路基沉降量以及发展规律,进而为路基的加固提供基础的方案 [4]。
(15)
(16)
端泄流量为
Q=|Q1|+|Q2|
(17)
1.3.3 摩擦力
轴颈表面的摩擦力为
(18)
摩擦因数为
(19)
1.3.4 工作力矩
倾斜轴承稳定运转所需工作力矩为
(20)
(21)
总力矩为
(22)
2 耦合方程的数值求解
由于文中采用的mRPS模型不受网格精度影响,为提高运行速度,将油膜沿周向和轴向划分为100×21个网格节点,通过Matlab进行仿真计算。
2.1 mRPS方程的离散化
(23)
考虑实际工况中气泡的接触融合导致气体充满整个单元,在迭代求解过程中,需要限制孔隙率αi,j不超过0.99。
2.2 雷诺方程离散化
为方便表达,令M=ρh3/(12μ),则雷诺方程可以改写为
(24)
经过中心差分后得到
Aijpi-1,j+Bijpi,j+Cijpi+1,j=Dij
(25)
其中
(26)
(27)
(28)
(29)
2.3 差分边界条件
对于mRPS方程,油膜端面处等于初始局部含气率
αi,1=αi,21=α0
(30)
对于雷诺方程,沿周向展开的油膜两端压力值与压力梯度值相等,即
(31)
油膜开始和结束处的导数分别采用前向差分和后向差分格式,即
(32)
2.4 求解流程
利用四阶龙格库塔法和托马斯算法求解耦合方程进而求解滑动轴承静特性参数,具体求解流程图如图2所示。
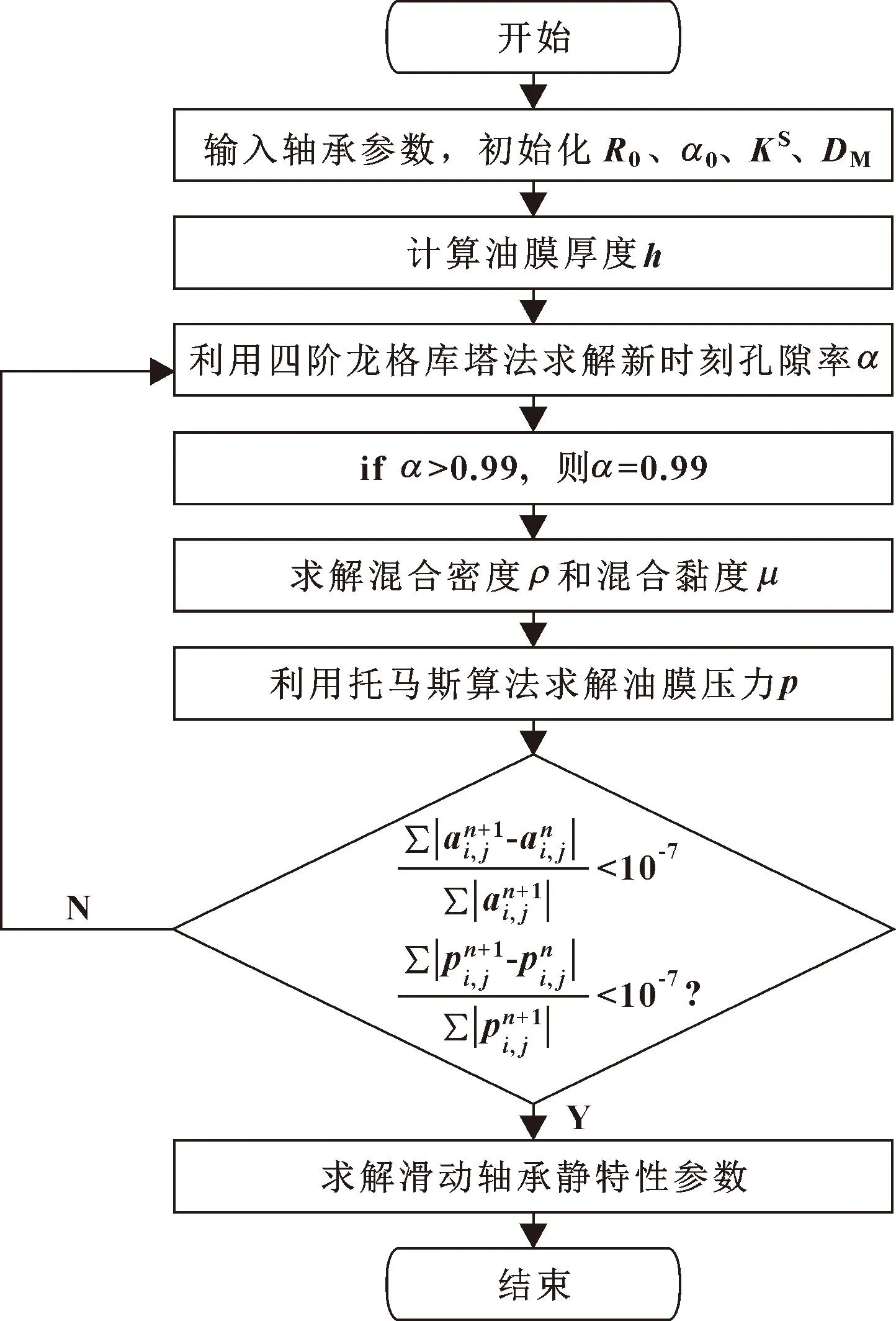
图2 滑动轴承计算流程Fig.2 Calculation flow of sliding bearing
3 仿真结果及分析
3.1 分析工况
仿真分析采用的径向滑动轴承主要参数如表1所示。
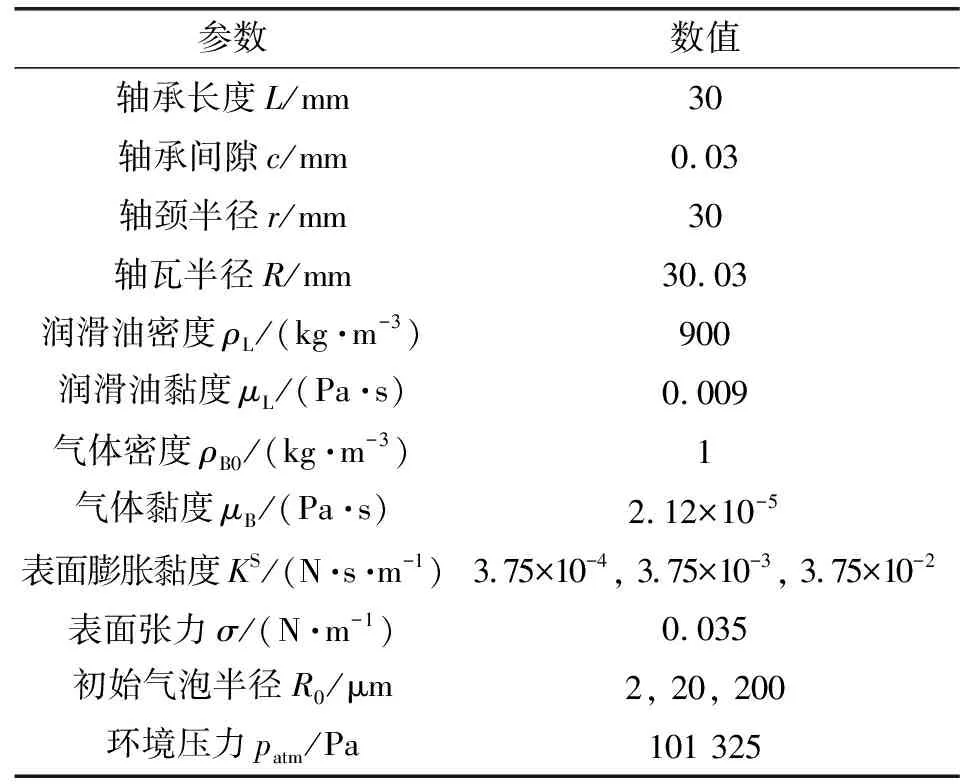
表1 径向滑动轴承基本参数
3.2 油气两相润滑与纯油润滑比较
首先比较油气两相流润滑和纯油润滑对轴承静特性影响,由于纯油中存在初始空化核,文中采用0.1%含气率的润滑油模拟纯油仿真,气泡参数为KS=3.75×10-3N·s/m,R0=20 μm,α0=1%。
图3所示为不同转速和偏心率下最大油膜压力随润滑油含气率的变化曲线,随含气率的增加,最大油膜力在低含气率下无明显变化,当初始含气率超过20%时,曲线呈现下降趋势。当含气率为定值时,随着转速的提高,最大油膜压力呈增加的趋势,这种趋势在大偏心率时更为明显。图4所示为不同转速和偏心率下油膜承载力随润滑油含气率的变化曲线,曲线变化趋势与图3大致相同。图5所示为不同转速和偏心率下端泄流量随润滑油含气率的变化曲线,端泄流量随含气率的增加呈下降趋势,由于转速提高润滑油流动速度加快以及大偏心率下楔形间隙中的挤压作用导致端泄流量在高转速大偏心率时增加,当转速为1 000 r/min,偏心率为0.4时,转速提高带来的影响大于偏心率增大带来的影响。图6所示为不同转速和偏心率下摩擦力随润滑油含气率的变化曲线,摩擦力随含气率的增加整体呈下降趋势,随含气率的提高摩擦力呈减小趋势。
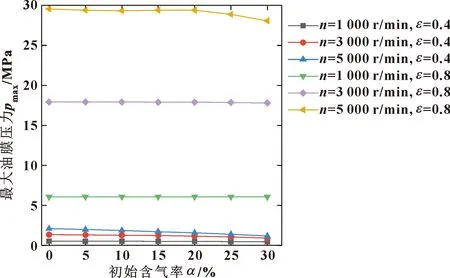
图3 不同转速和偏心率下最大油膜压力随含气率的变化Fig.3 Variation of maximum oil film pressure with gas holdup at different rotational speeds and eccentricities
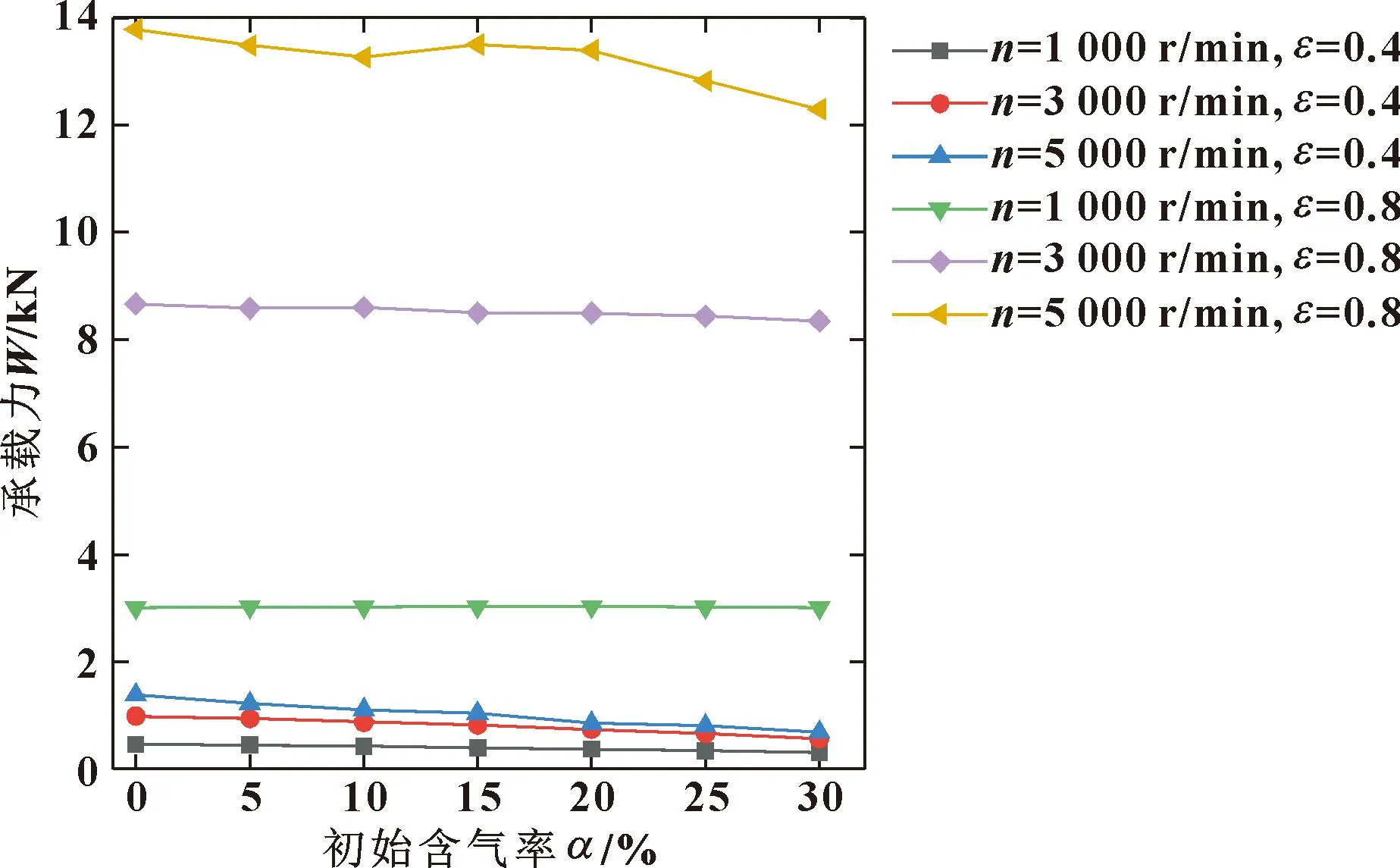
图4 不同转速和偏心率下承载力随含气率的变化Fig.4 Variation of bearing capacity with gas holdup at different rotational speeds and eccentricities
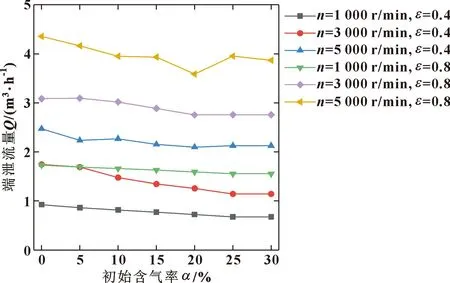
图5 不同转速和偏心率下端泄流量随含气率的变化Fig.5 Variation of leakage flow at the lower end with gas holdup at different rotational speeds and eccentricities
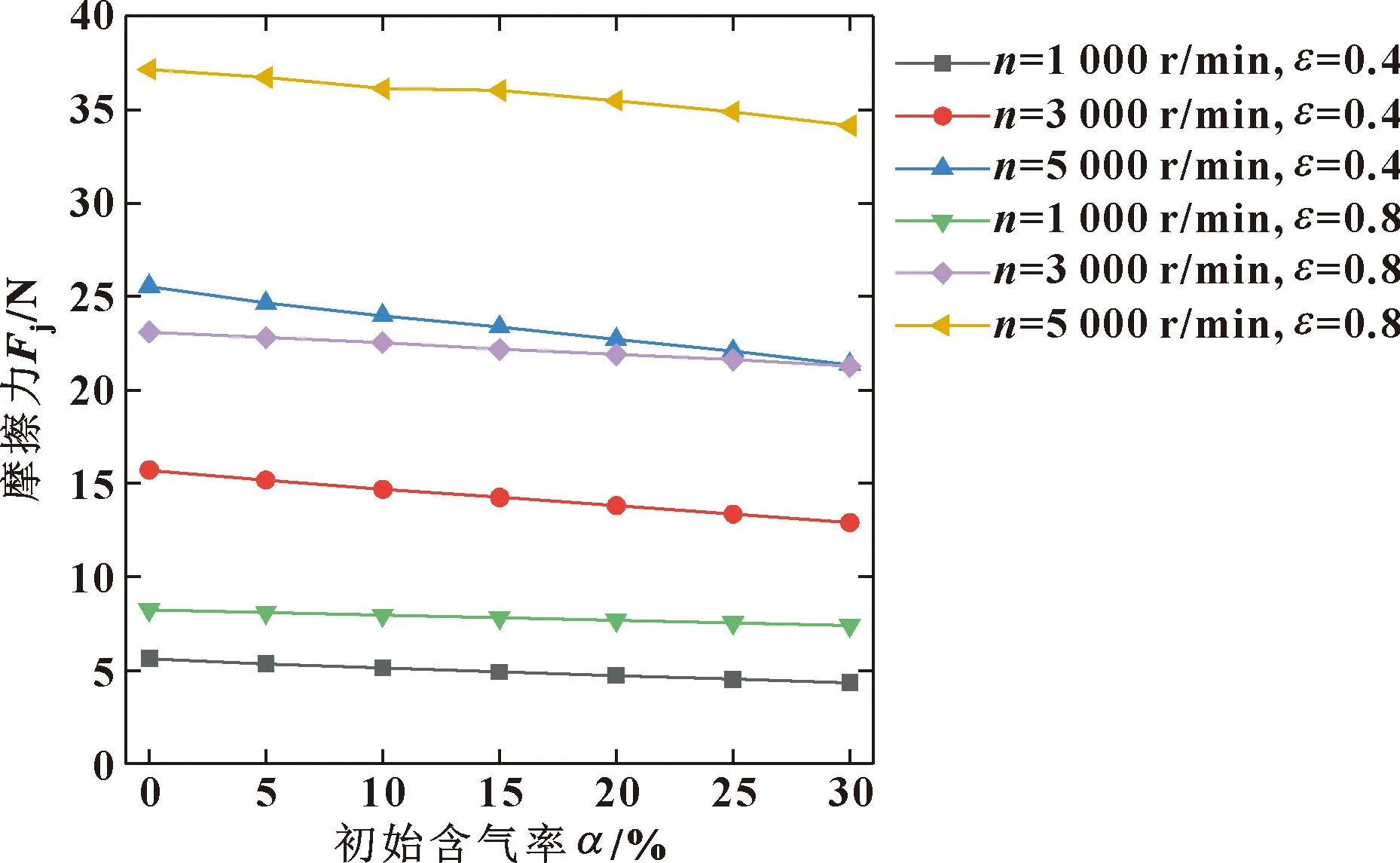
图6 不同转速和偏心率下摩擦力随含气率的变化Fig.6 Variation of frictional force with gas holdup at different rotational speeds and eccentricities
总体来看,随着含气率的增加,润滑油中气泡的存在会降低最大油膜压力、承载力、端泄流量和摩擦力,当含气率较小时,这种影响对油膜压力与承载力的影响并不显著。如从降低磨损、减少供油的角度看,在适当的转速与较大偏心率时,油气润滑会产生有利的影响。考虑油气润滑中空泡运动的复杂性,下文将通过改变气泡的参数进行仿真以进一步探究油气润滑对滑动轴承静特性的影响。
3.3 气泡参数对油气润滑的影响
采用文献[17]的参数设置,将表面膨胀黏度和初始气泡半径分别设为3个数量级并以中间数量级作为参考,通过改变两参数的值探究其对油膜承载力以及摩擦力的影响。
图7显示的是主轴转速为1 500 r/min时,不同膨胀黏度和不同气泡初始半径下油膜承载力随偏心率的变化曲线,可知在中低偏心率时增大膨胀黏度与减小初始气泡体积会产生相同的效果。这是因为表面膨胀黏度的存在会产生阻碍气泡生长的力,当偏心率小于0.6时,增大膨胀黏度和减小气泡初始半径会使气泡抵抗膨胀的作用增强,从而可使气泡承受一定的载荷导致油膜承载力增大;而当偏心率大于0.6时,增大膨胀黏度和减小气泡初始半径反而会减小油膜承载力,这是因为在大偏心率时,油膜压力过大会压缩气体致使在油膜间隙最小处的部分气泡产生破裂,从而使承载力降低。
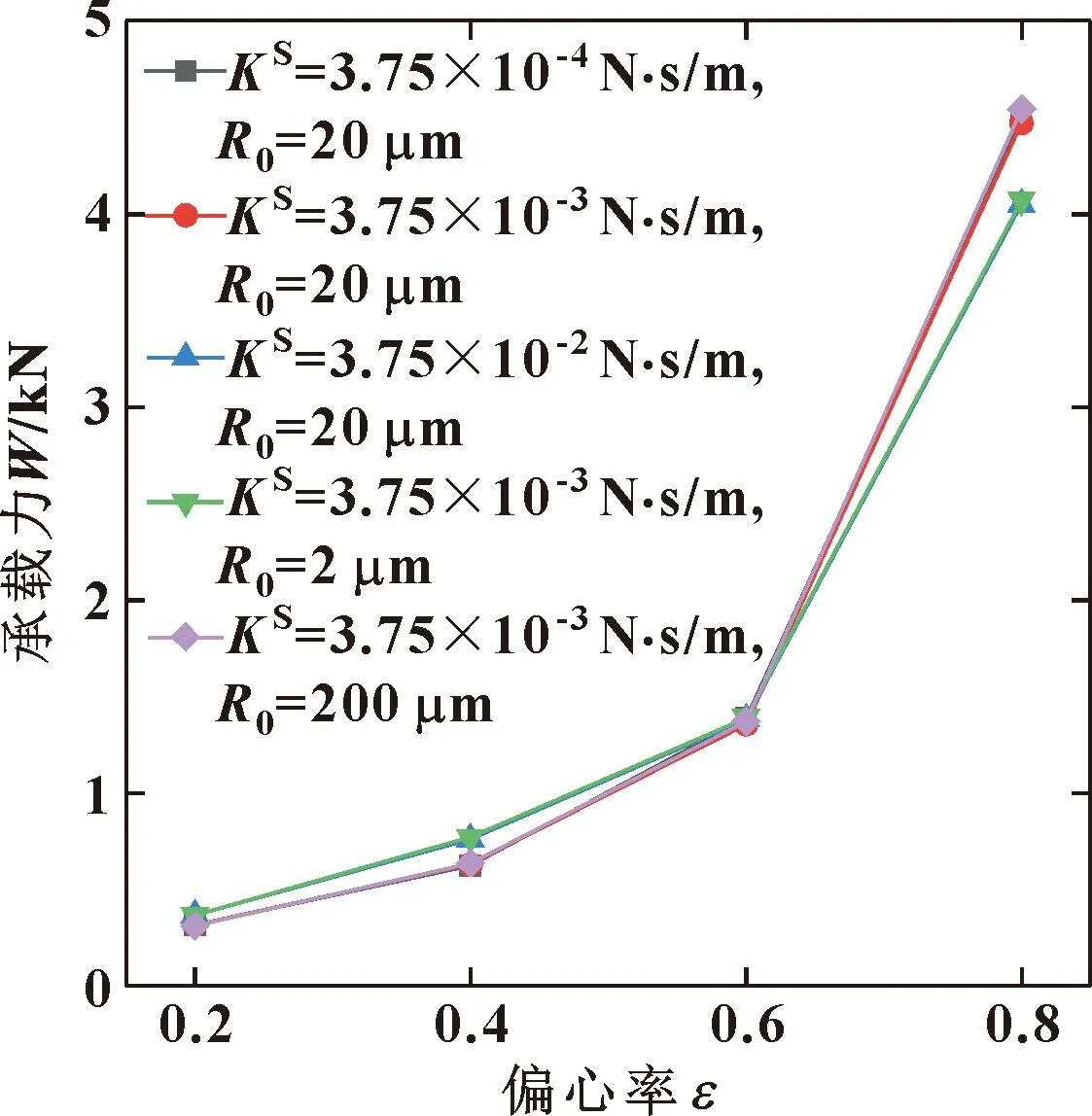
图7 不同气泡参数下承载力随偏心率的变化(1 500 r/min)Fig.7 Variation of bearing capacity with eccentricity under different bubble parameters(1 500 r/min)
图8所示为主轴转速为1 500 r/min时,不同膨胀黏度和不同气泡初始半径下摩擦力随偏心率的变化曲线,增大表面膨胀黏度和减小气泡初始半径会增大摩擦力,这是因为表面膨胀黏度项带来的影响是抵抗气泡形状变化。当气泡半径较小膨胀黏度较大时,气泡不易产生变形,油膜内部黏滞作用增强,气泡表面会与润滑剂产生额外的摩擦力。

图8 不同气泡参数下摩擦力随偏心率的变化(1 500 r/min)Fig.8 Variation of frictional force with eccentricity under different bubble parameters(1 500 r/min)
图9(a)所示为主轴转速1 000 r/min、偏心率0.4、气泡半径20 μm、表面膨胀黏度3.75×10-3N·s/m条件下,初始含气率1%时的油膜压力与单元含气率叠加的等高线图,图9(b)所示为相同条件下初始含气率5%时的油膜压力与单元空穴率叠加的等高线图。当含气率增加时,等高线云图显示两者油膜压力分布近似,但空穴区域面积会变大。图10所示为主轴转速1 000 r/min、偏心率0.4、含气率1%条件下,不同气泡参数下油膜压力与单元含气率等高线图,其中图10(a)与图9(a)其他条件相同,仅表面膨胀黏度增加一个数量级(KS=3.75×10-2N·s/m)的等高线图,图10(b)仅气泡初始半径降低一个数量级(R0=2 μm)的等高线图。可见2种工况下油膜压力云图与单元含气率等高线几乎相同,这也再次验证了表面膨胀黏度可增加气泡抵抗变形的作用。相比于参考工况,增大膨胀黏度或减小气泡半径会降低油膜单元空隙率,同时也会大幅度增加油膜负压区。总的来看,增大表面膨胀黏度和减小气泡初始半径对径向滑动轴承会产生相同的润滑效果,而当两者均减小一个数量级时与参考变量相差不大,为此在后续引入轴颈倾斜影响时,文中忽略影响较小的变量值。
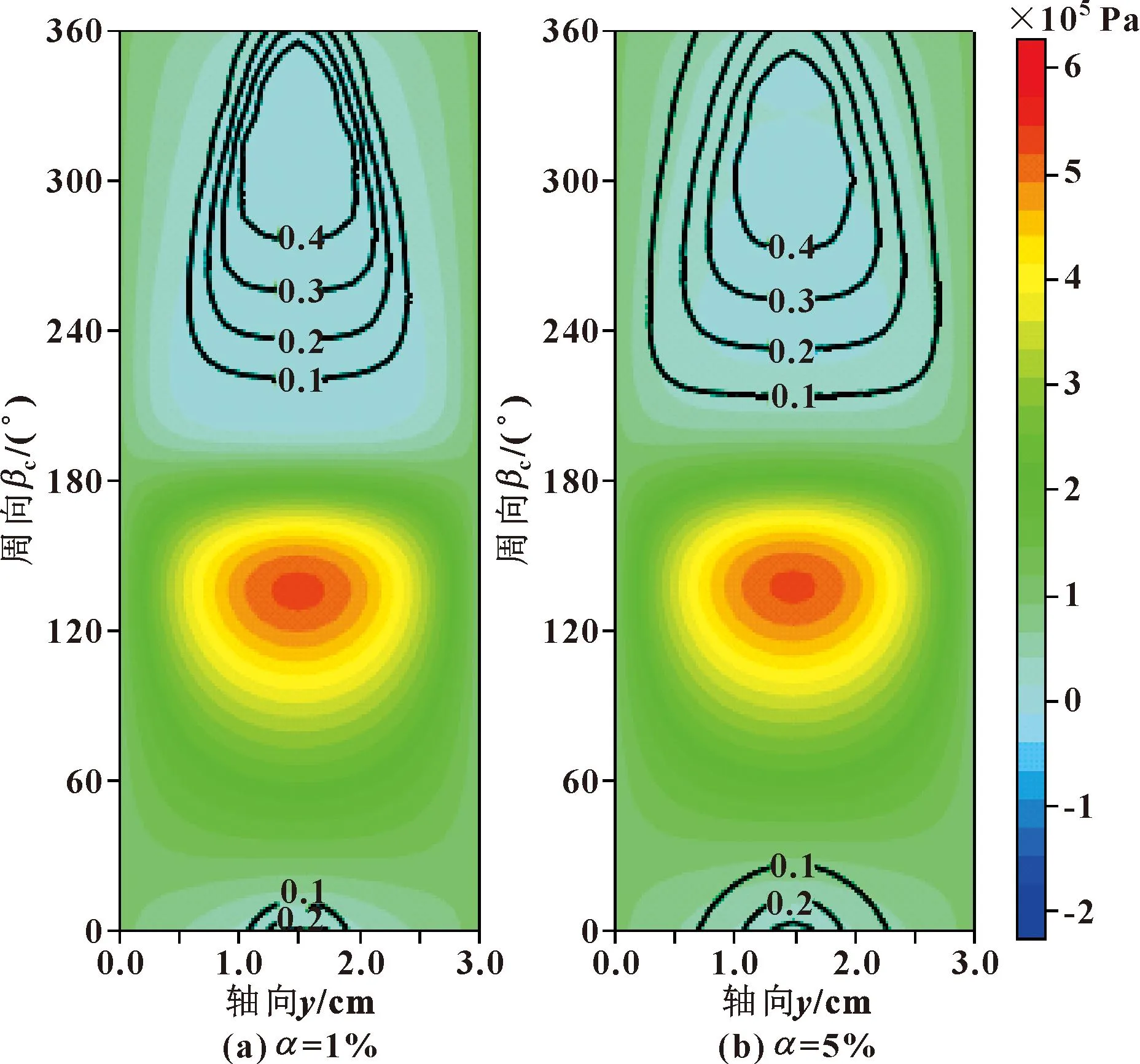
图9 不同含气率下油膜压力与单元含气率等高线图 (n=1 000 r/min,ε=0.4,KS=3.75×10-3 N·s/m,R0=20 μm)Fig.9 Contour diagram of oil film pressure and unit gas holdup under different gas holdup(n=1 000 r/min,ε=0.4,KS=3.75× 10-3 N·s/m,R0=20 μm):(a)α=1%;(b)α=5%

图10 不同气泡参数下油膜压力与单元含气率等高线图 (n=1 000 r/min,ε=0.4,α=1%)
3.4 轴颈倾斜程度对油膜压力的影响
图11所示的是主轴转速为1 000 r/min、偏心率为0.4时,轴颈不发生倾斜时的油膜压力分布与油膜厚度分布。图12所示为主轴转速为1 000 r/min,轴颈倾斜程度等于0.8时的油膜压力分布与油膜厚度分布。当轴颈发生倾斜时,油膜压力和油膜厚度在形状与数值上均有很大变化,所以将轴颈倾斜计入轴承润滑特性分析中很有必要,下文将在相同工况下进行进一步仿真。
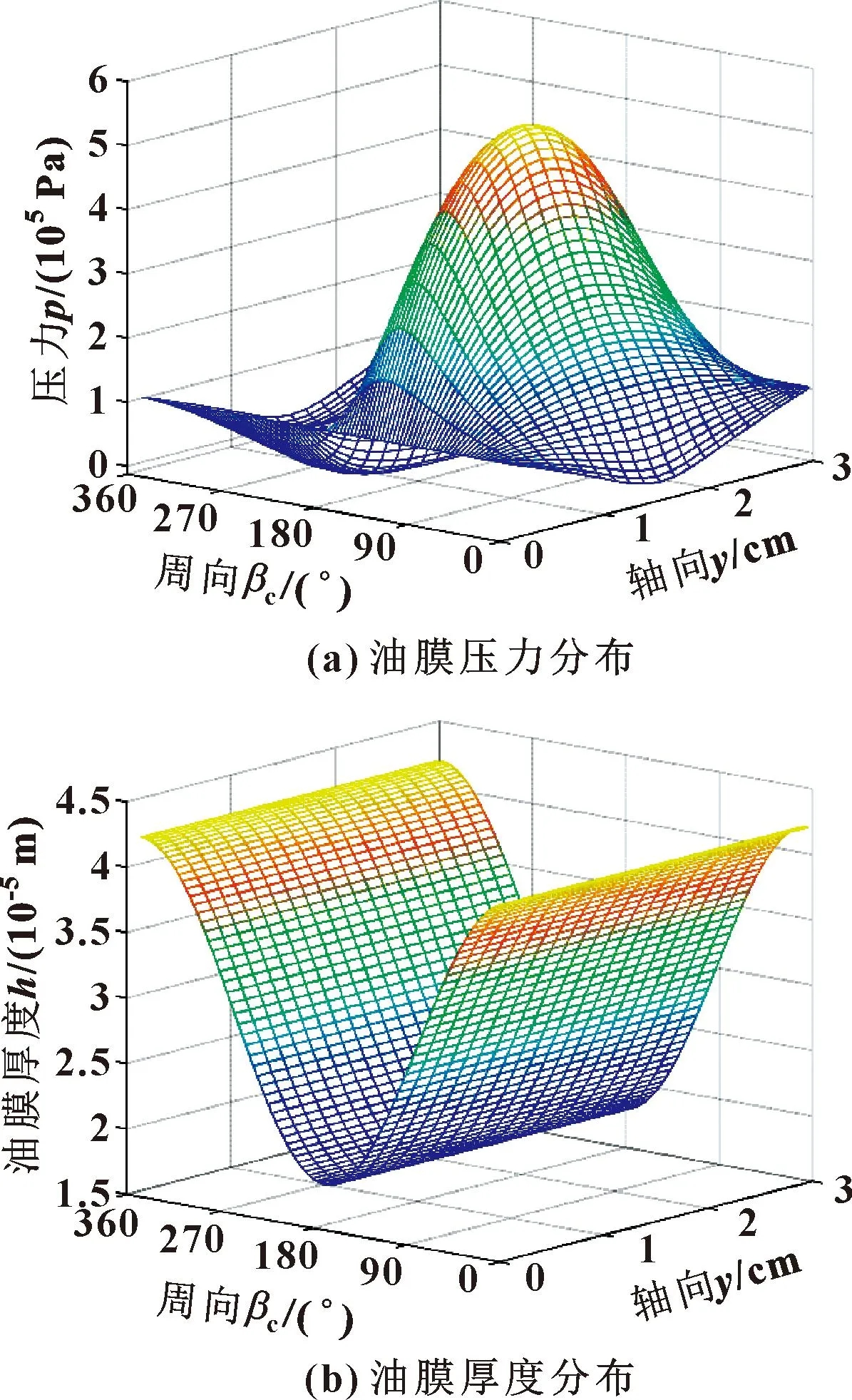
图11 轴颈无倾斜时油膜压力和厚度分布Fig.11 Oil film pressure(a) and oil film thickness(b) distribution of the bearing without journal inclination
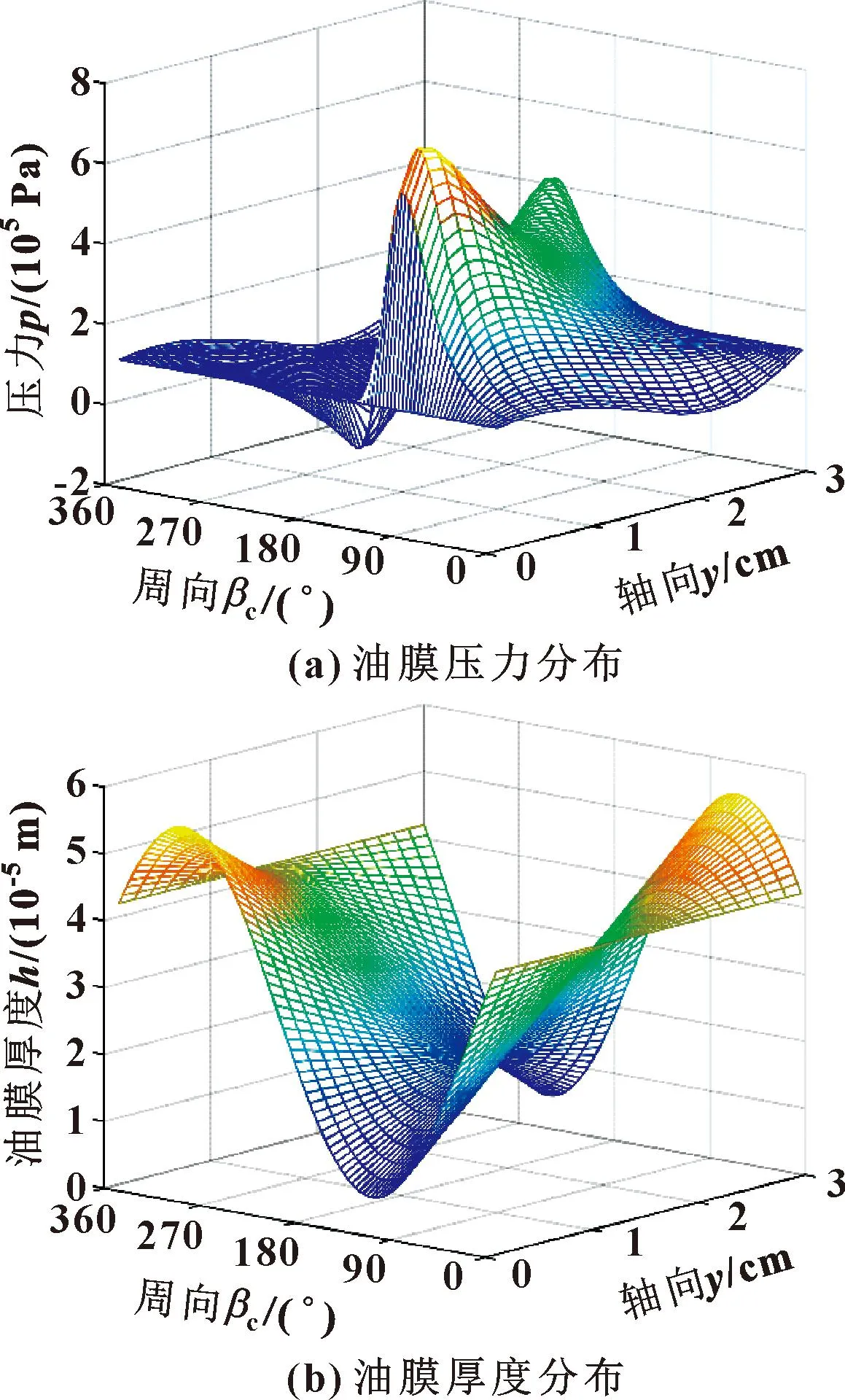
图12 轴颈倾斜程度为0.8时油膜压力和厚度分布Fig.12 Oil film pressure(a) and oil film thickness(b) distribution of the bearing when journal inclination degree is 0.8
图13所示为当采用纯油润滑时,不同倾斜程度下的油膜压力与单元含气率的等高线叠加云图,随着轴颈倾斜程度的增加,油膜压力呈倾斜分布,油膜压力数值逐渐增大且最大值沿周向与轴向发生移动,这是由于当轴颈发生倾斜时,油膜在沿周向的不同位置和沿轴向的不同截面处均发生数值改变。当轴颈产生倾斜时,空化区形状发生变化,空化区面积也随倾斜程度的增加而增加,空化区域的边界更接近轴承的端面处。当轴颈倾斜程度小于0.6时,最大油膜压力数值变化较小,当轴颈倾斜程度到0.8时,最大油膜压力显著增加。轴颈倾斜会改变油膜在各个截面处的数值从而影响微小气泡的分布和运动,所以研究油气润滑时有必要考虑轴颈倾斜因素。
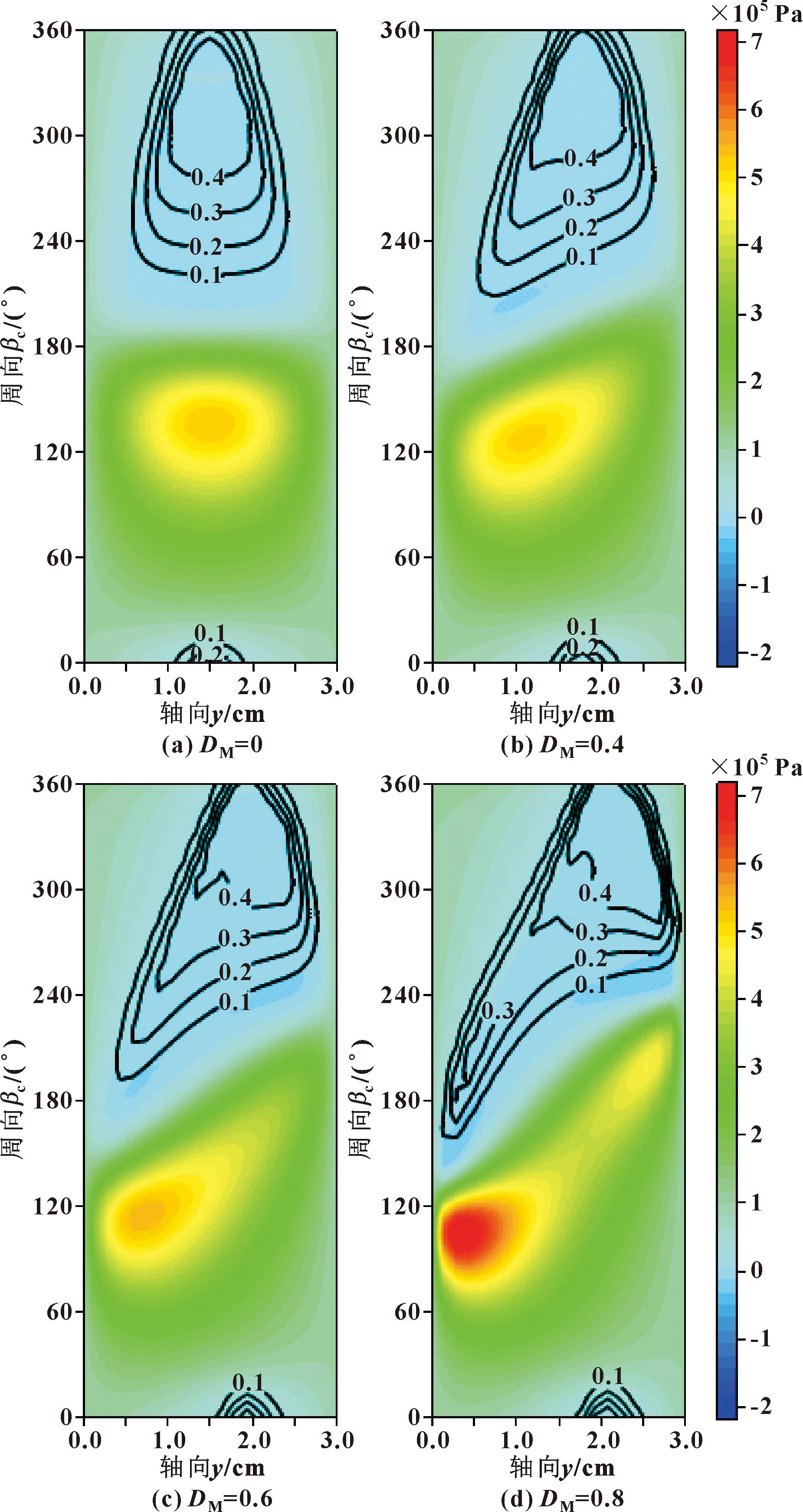
图13 轴颈倾斜程度下油膜压力与单元含气率等高线图Fig.13 Contour diagram of oil film pressure and unit gas holdup at different journal inclination degree:(a)DM=0; (b)DM=0.4;(c)DM=0.6;(d)DM=0.8
3.5 表面膨胀黏度与倾斜程度对轴承润滑性能的影响
图14与图15分别显示的是不同偏心率和表面膨胀黏度下最大油膜力与承载力随倾斜程度变化的曲线。当偏心率小于0.6时,增大表面膨胀黏度会小幅度增大油膜压力以及承载力;但当偏心率为0.8时,表面膨胀黏度的增大反而会减小油膜压力及承载力。图16所示是不同偏心率和膨胀黏度下端泄流量随倾斜程度的变化。可知,端泄流量随着倾斜程度的增加而增加,在大偏心工况下,表面膨胀黏度带来的影响与计入轴颈倾斜带来的影响相当;当偏心率下降至0.2时,表面膨胀黏度对端泄流量没有显著影响;在中高偏心率下,表面膨胀黏度增加一个数量级会增大端泄流量。
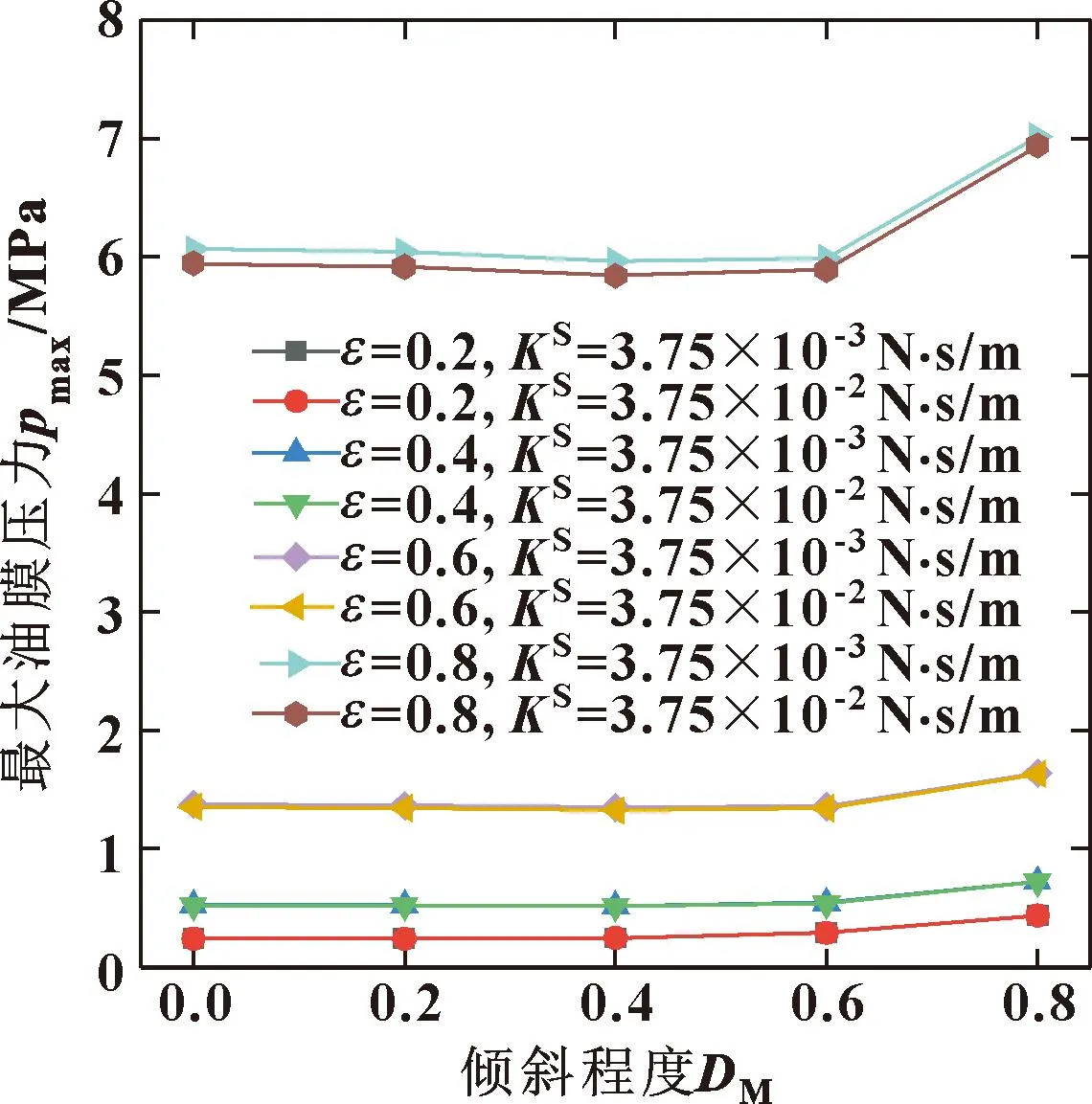
图14 不同偏心率和膨胀黏度下最大油膜压力随倾斜 程度的变化Fig.14 Variation of maximum oil film pressure with inclination degree under different eccentricity and different swelling viscosity
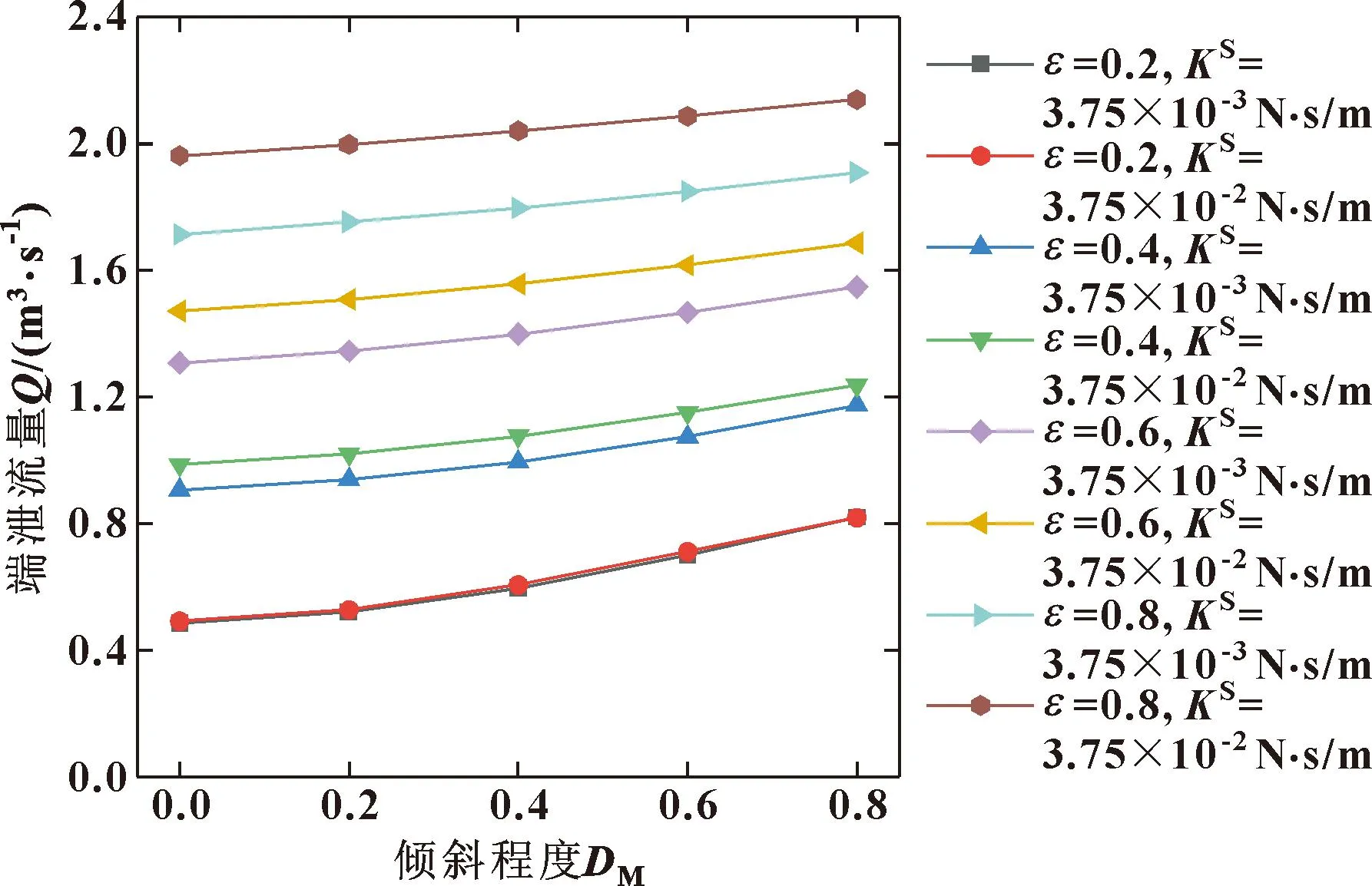
图16 不同偏心率和膨胀黏度下端泄流量随倾斜程度的变化Fig.16 Variation of lower end leakage with different eccentricity and different swelling viscosity with the degree of inclination
图17显示的摩擦力随工况的变化与端泄流量的变化趋势相同。图18所示为不同偏心率和膨胀黏度下摩擦因数随倾斜程度的变化。
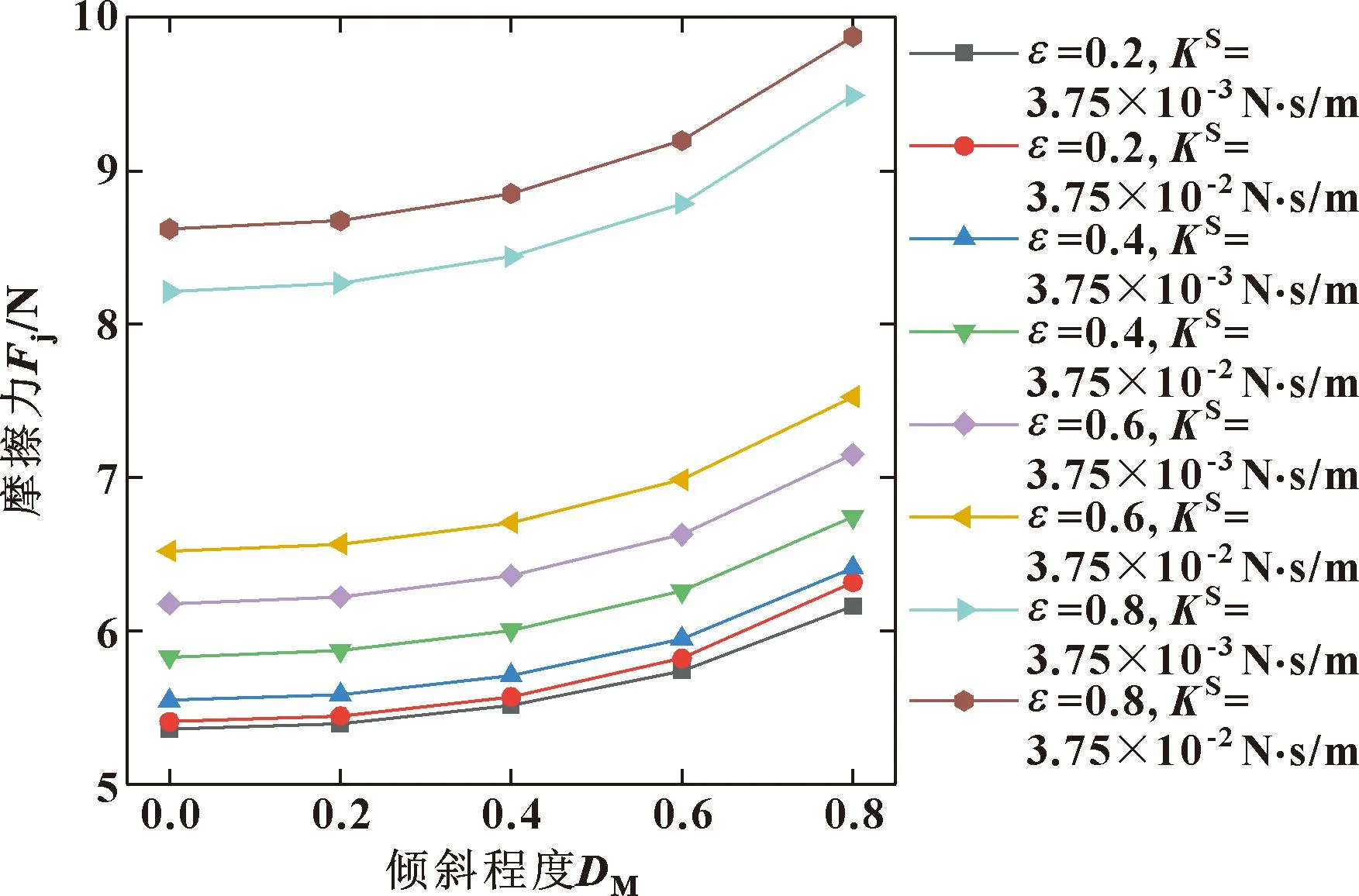
图17 不同偏心率和膨胀黏度下摩擦力随倾斜程度的变化Fig.17 Variation of frictional force with inclination degree under different eccentricity and different swelling viscosity
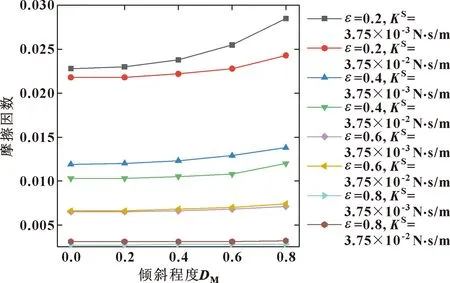
图18 不同偏心率和膨胀黏度下摩擦因数随倾斜程度的变化Fig.18 Variation of friction coefficient with inclination degree under different eccentricity and different swelling viscosity
可知,在低偏心率下,增大表面膨胀黏度会减小摩擦因数,在大偏心率下,摩擦因数几乎不变。这表明增大表面膨胀黏度对油气润滑会产生一定的减摩效果,这种效果在低偏心率下更为明显。图19显示的是轴承稳定运转所需工作力矩随倾斜程度的变化曲线。可知,当轴颈倾斜程度较大时,工作力矩会显著增加。表面膨胀黏度的增加会降低工作力矩,这在中高偏心率时表现得更为明显。
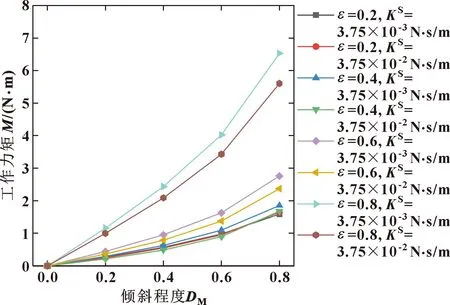
图19 不同偏心率和膨胀黏度下工作力矩随倾斜程度的变化Fig.19 Variation of working moment with inclination degree under different eccentricity and different swelling viscosity
3.6 含气率与倾斜程度对轴承润滑性能的影响
图20显示的是不同偏心率和初始含气率下,最大油膜压力随轴颈倾斜程度变化的曲线。
由图20可以看出,仿真设置的2个含气率数值对轴承油膜压力影响几乎相同,偏心率改变对油膜压力的影响大于轴颈倾斜带来的影响。最大油膜压力在不对中度小于0.6时变化较小,当倾斜程度达到0.8时数值会显著增加。图21显示的是不同偏心率和初始含气率工况下,油膜承载力随轴颈倾斜程度变化的曲线。可知,当含气率增加时,在低偏心下,油膜承载力有小幅度降低,而在大偏心率时,油膜承载力有小幅度增加且不对中度带来的影响较大。
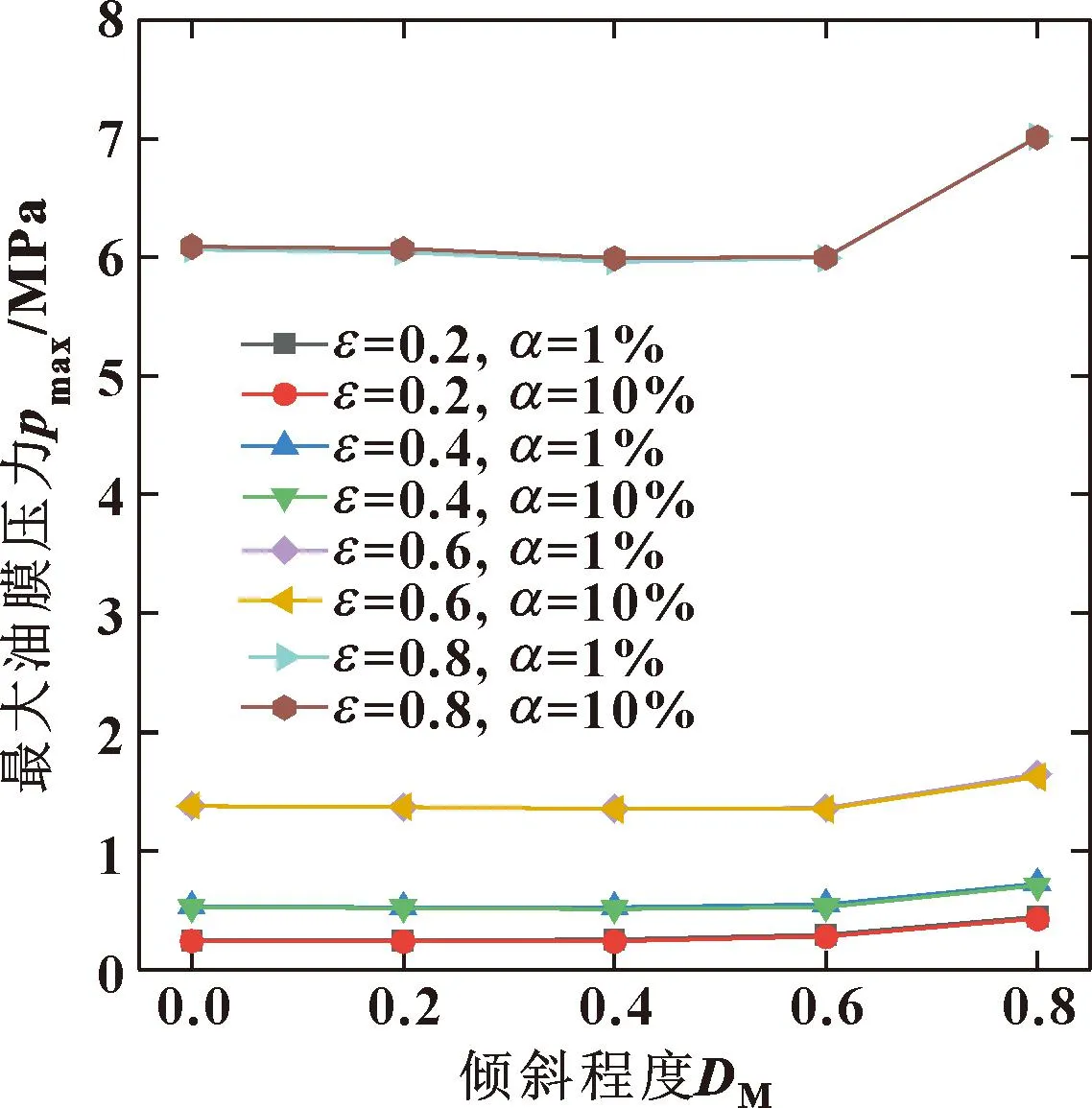
图20 不同偏心率和含气率下最大油膜压力随倾斜程度的变化Fig.20 Variation of maximum oil film pressure with inclination degree under different eccentricity and different gas holdup
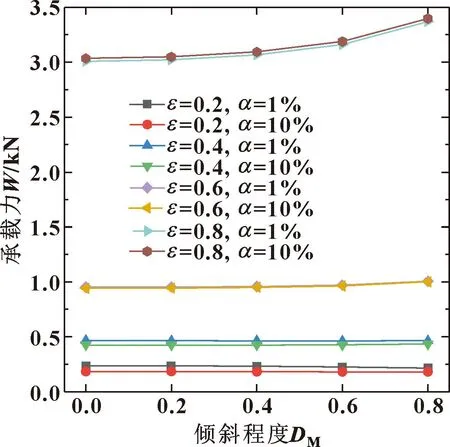
图21 不同偏心率和含气率下摩擦力随倾斜程度的变化Fig.21 Variation of frictional force with inclination degree under different eccentricity and different gas holdup
图22所示为端泄流量随轴颈倾斜程度的变化曲线。从总体上看,含气率的增加会降低端泄流量,端泄流量随轴颈倾斜程度的增大而增大。偏心率增大以及倾斜程度增大导致楔形间隙动压效果增强从而导致端泄流量增加,且这2种影响在数值上相当。
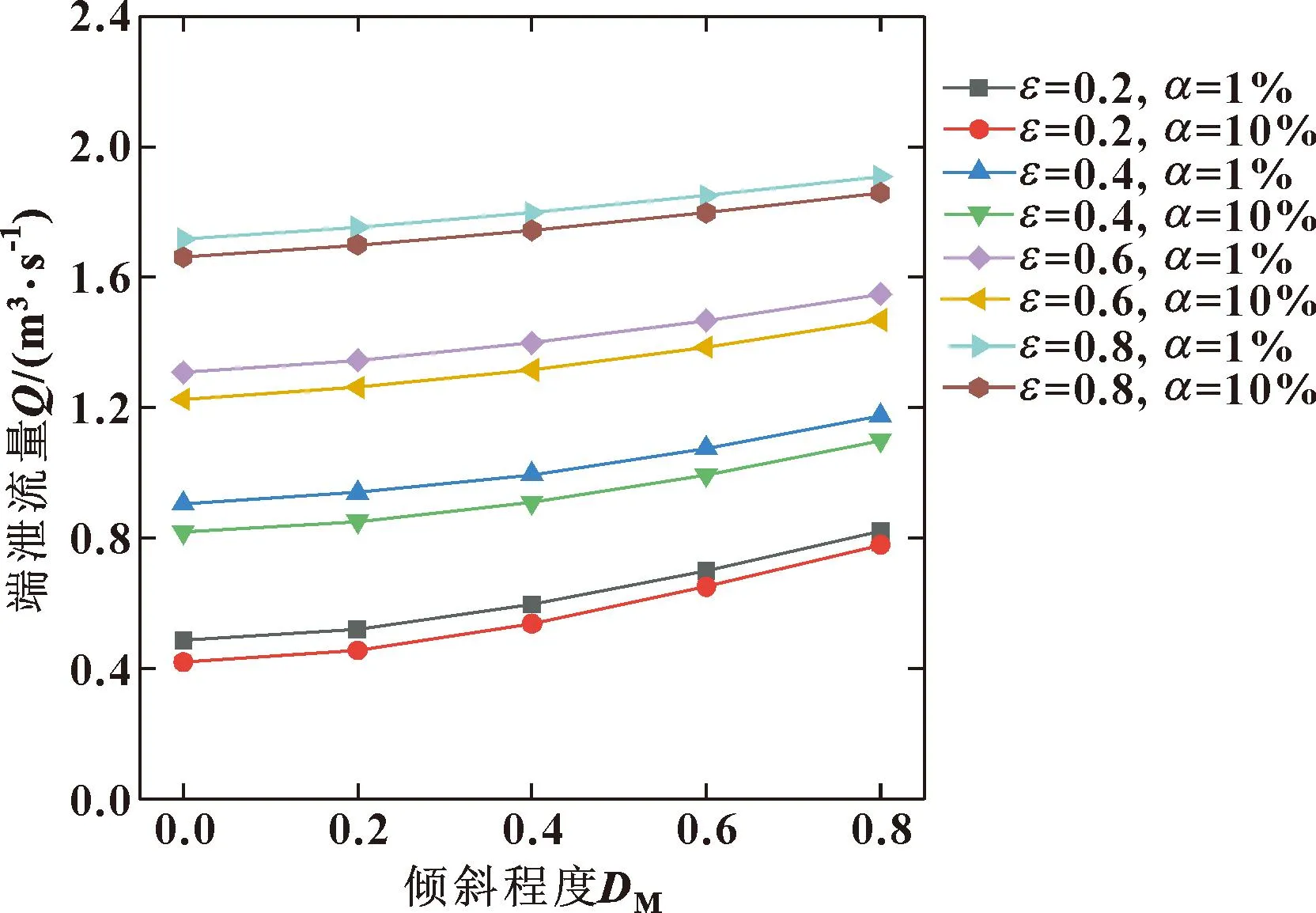
图22 不同偏心率和含气率下端泄流量随倾斜程度的变化Fig.22 Variation of the discharge volume at the lower end with inclination degree under different eccentricity and different gas holdup
图23和图24分别为摩擦力和摩擦因数随轴颈倾斜程度的变化曲线。摩擦力的变化趋势与端泄流量大体相同,轴颈倾斜带来的影响与偏心率相当;当偏心率较大时,摩擦力增加的数值会更加显著。而摩擦因数随着倾斜程度的增大而增大,随着偏心率的增大而减小;含气率的增加会在低偏心率时降低摩擦因数,而在大偏心率时摩擦因数会有小幅度的增加。图25显示的是不同偏心率和初始含气率工况下,轴承稳定工作所需力矩随轴颈倾斜程度变化的曲线。轴颈倾斜程度的增大和偏心率的增大都会导致工作力矩逐渐增大,含气率增加一个数量级会使轴承在低偏心工况下数值降低,在中高偏心下数值有小幅度提高。
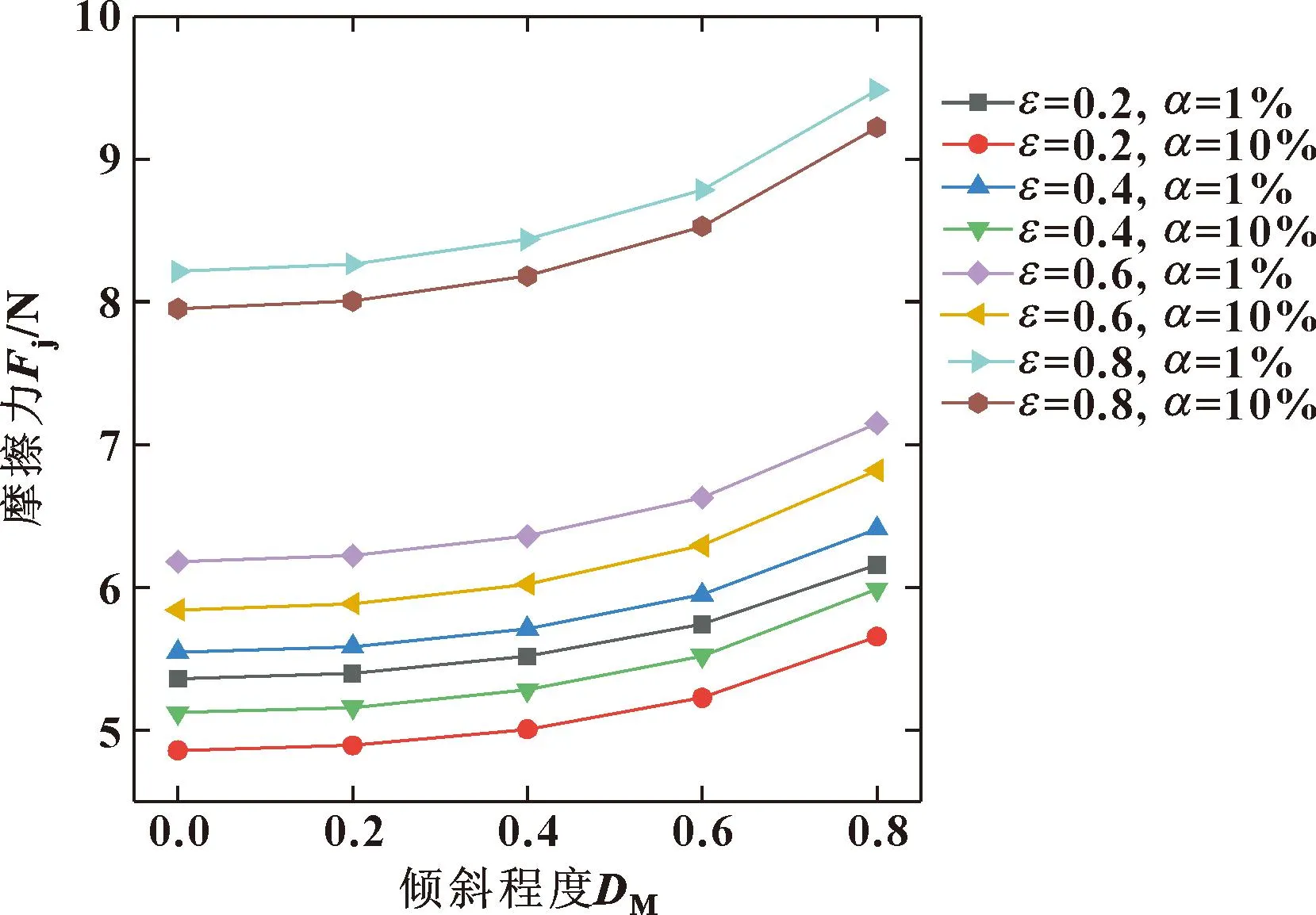
图23 不同偏心率和含气率下摩擦力随倾斜程度的变化Fig.23 Variation of frictional force with inclination degree under different eccentricity and different gas holdup
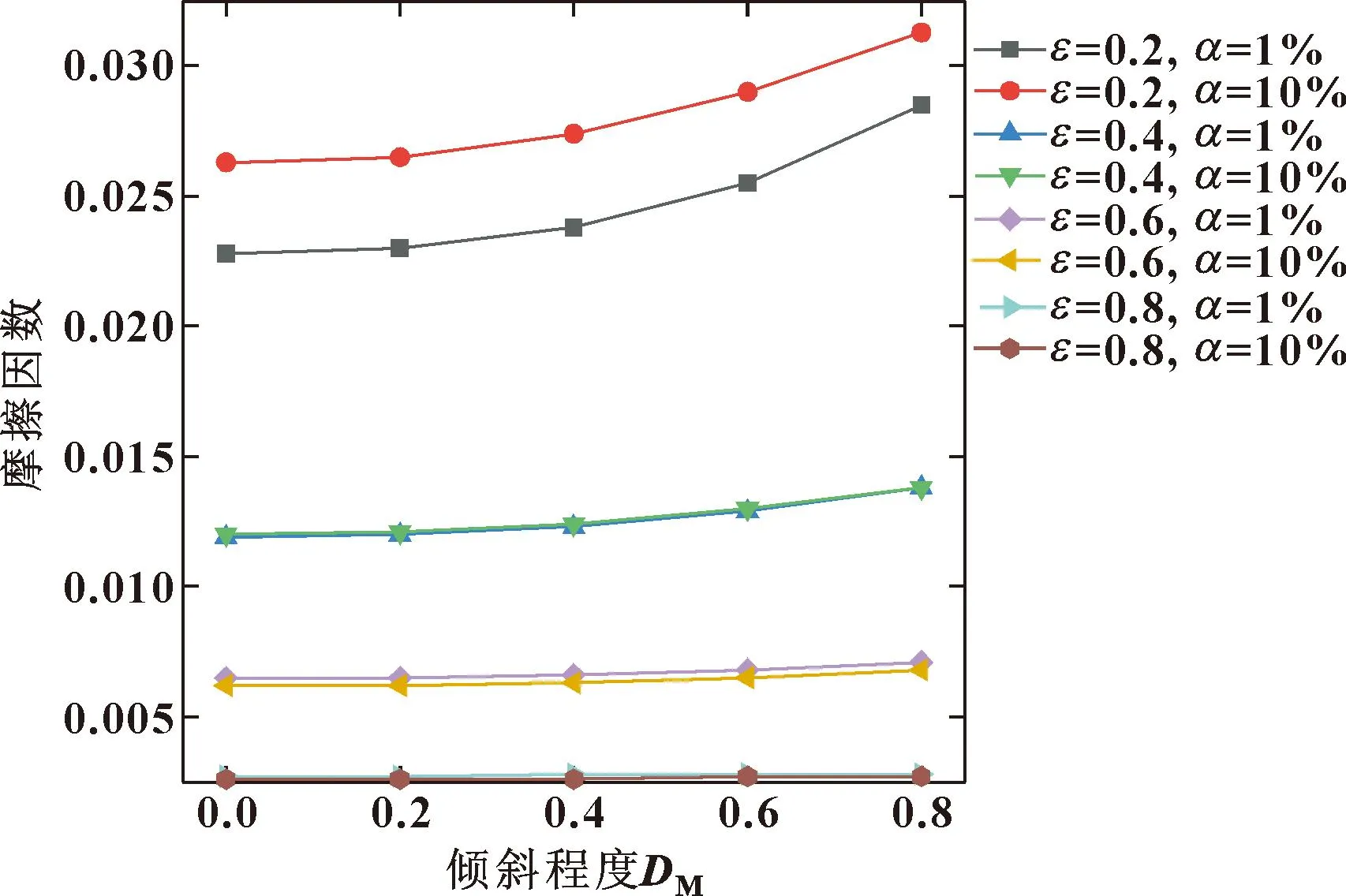
图24 不同偏心率和含气率下摩擦因数随倾斜程度的变化Fig.24 Variation of friction coefficient with inclination degree under different eccentricity and different gas holdup
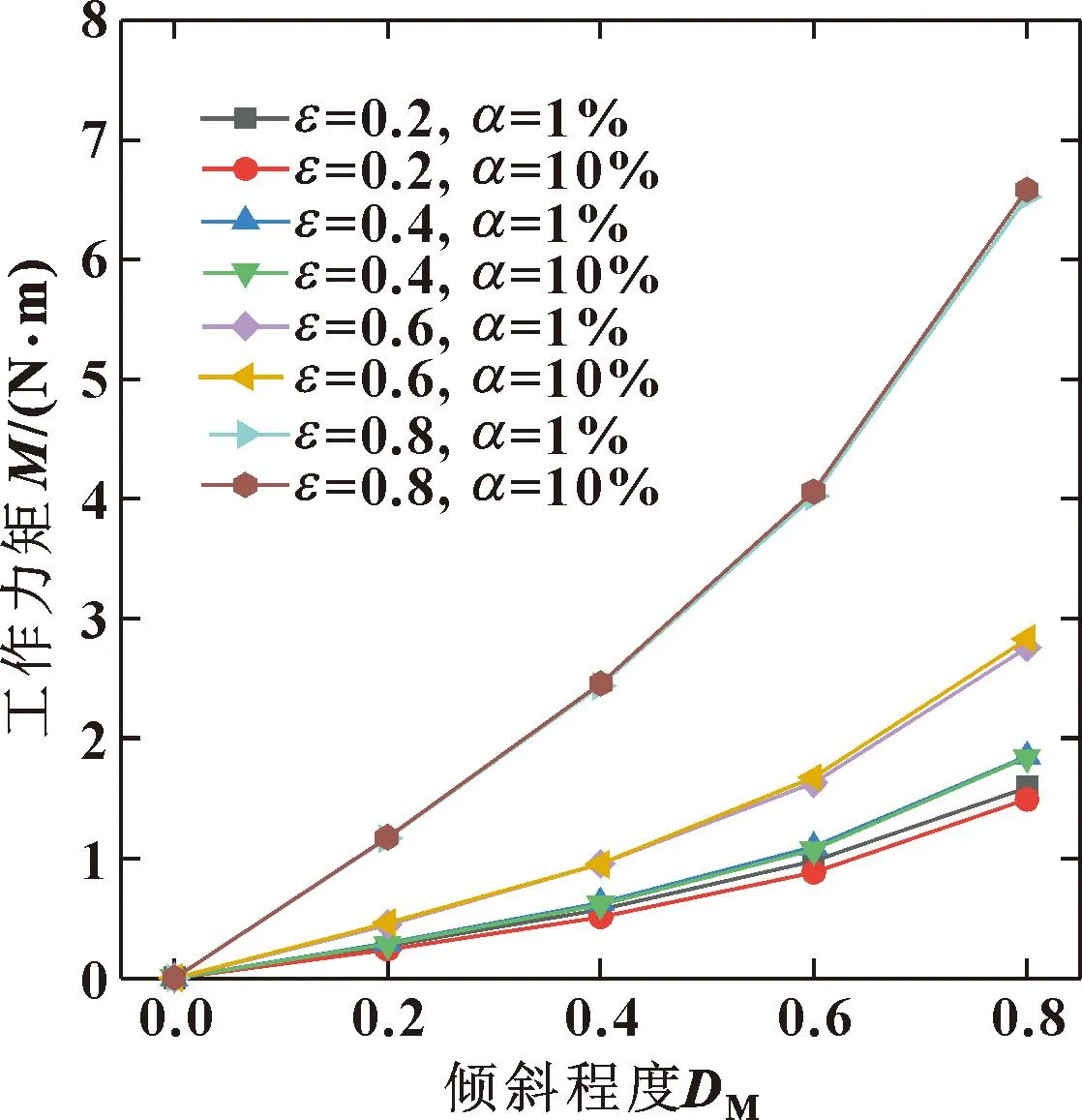
图25 不同偏心率和含气率下工作力矩随倾斜程度的变化Fig.25 Variation of working moment with inclination degree under different eccentricity and different gas holdup
4 结论
(1)油气润滑条件下在一定的含气率范围内,随着含气率的增高,径向滑动轴承最大油膜压力、承载力、端泄流量和摩擦力都会减小。
(2)不同的气泡参数对轴承润滑特性的影响不同,增大膨胀黏度和减小气泡半径在中低偏心率下会提高油膜承载力,而在大偏心率下会使油膜承载力降低。
(3)轴颈倾斜会改变油膜压力与空穴分布,随着倾斜程度的增加,最大油膜压力、承载力、端泄流量、摩擦力和工作力矩都会增大。通过改变气泡参数和润滑油含气率可适当削弱轴颈倾斜带来的影响。
(4)考虑润滑剂为含气油液的复杂性,需要通过后续的实验进一步探究油气润滑对径向滑动轴承润滑特性的影响。
