一种滑动检测算法下的滑坡位移时序分解方法

2024-03-12曾怀恩涂鹏飞

长江科学院院报 2024年3期

冯谕,曾怀恩,2,3,涂鹏飞,3

(1.三峡大学土木与建筑学院,湖北宜昌 443002;2.三峡大学湖北长江三峡滑坡国家野外科学观测研究站,湖北宜昌 443002; 3.三峡大学湖北省水电工程施工与管理重点实验室,湖北宜昌 443002)

0 引言

三峡库区一直是我国地质灾害多发区,滑坡灾害的高发性与高危性使得其成为三峡库区最具破坏力的自然灾害,严重的滑坡灾害对人民生活造成了重大影响。滑坡地表水平位移预测一直是众多专家学者研究防治滑坡灾害的有效手段。对于“阶跃式”滑坡位移的预测,目前大多数学者采用的是经时序分解后的机器学习预测方法。因此,合理地对滑坡位移进行时序分解是决定模型预测精确性、解释性、运用合理性的重要手段。

目前已有的时序分解方法主要有:2022年陈曦[1]提出的一种滑坡每期位移变化量与位移变化均值作比较,剔除阶跃项,并应用多项式拟合的方法;二次移动平均提取趋势项并应用多项式拟合方法(2022年曹博等[2]应用于八字门滑坡位移预测);三次移动平均提取趋势项并应用多项式拟合方法(2015年周超等[3]应用于八字门滑坡位移预测);二次指数平滑法提取趋势项并应用多项式拟合方法(2018年黄发明等[4]应用于白水河滑坡位移预测);变分模态分解(Variational Mode Decomposition,VMD)趋势分解法(2019年赵力学等[5]用于河流流量预测);Cox-Stuart检验趋势分解法(2020年胡成雨等[6]用于产品质量检验);多项式最小二乘分解法等。

三峡库区白水河、八字门等典型滑坡都属于“阶跃式”滑坡。上述方法下的滑坡位移预测虽然在短期内相对精确,但其分解方法未考虑到滑坡最重要的阶跃项位移。这致使在之后的滑坡位移预测中,可能因波动项位移包含有阶跃项位移而造成预测不精确,同时,多项式拟合与线性拟合无法对滑坡位移的趋势作出合理的力学解释。因此,应对现有滑坡位移数据进行阶跃项(突变点)检测,并选择滑坡蠕滑力学本构模型作为时序分解趋势项的合理拟合模型。现有的突变点检测方法主要有:Mann-Kendall突变检测方法(2022年邵骏等[7]应用于金沙江上游河段水温变化突变检测研究);滑动t检验突变检测方法(2021年欧阳卫等[8]应用于沣河径流量突变分析);启发式分割(Bernaola Galvan, BG)算法突变检验方法(2005年封国林等[9]应用于气候突变检测研究);pettitt突变检测方法(2014年傅丽昕[10]应用于丰县气温与降水量趋势性与突变特征检测);Yamamoto突变检测方法(2007年张建军等[11]应用于合肥年平均气温与年平均降雨突变检测分析);Bayes突变检测方法(2007年隋学深等[12]应用于沪深两市股指时序突变点研究)等。这些突变检测方法对于具有单调变化趋势的滑坡位移来说,适用性较差。

鉴于此,本文根据西原蠕变本构模型与自适应改进遗传算法模型,提出一种基于滑动t检验的滑动Rnl(曲线拟合优度)阶跃检测方法及改进移动平均修正与提取阶跃项位移方法,并将其应用于白水河滑坡水平位移时序分解。

1 理论和方法

1.1 滑坡位移时序分解

建立新型滑坡位移时序加法模型[13],即

F(t)=c(t)+w(t)+m(t) 。

(1)

式中:t为时间变量;F(t)为滑坡体变形水平位移;c(t)为以滑坡自重应力为主的地质应力作用引起的蠕滑趋势项位移;m(t)为强降雨、库水位剧烈变动等地质因素引起的阶跃项位移;w(t)为其他因素引起的波动项位移。

c(t)为滑坡蠕滑位移本构模型关系式;w(t)为周期项误差波动关系式;m(t)表达式为

m(t)=

(2)

式中:x为未产生阶跃的累积天数;y为产生阶跃的累积天数;r(t)为降雨量;v(t)为库水位变动速率;rq与vq分别为降雨量与库水位的阶跃阈值;f为以r(t)及v(t)为变量的阶跃函数。

本文认为r(t)或v(t)达到阶跃阈值(rq,vq)时,产生阶跃项位移fi(r(t),v(t));阶跃项位移具有累积效应,且不可逆,故有

x+y=n。

(3)

式中n为分析总期数。

1.2 滑坡蠕滑位移本构模型

文献[14]—文献[16]验证了西原模型对于滑坡位移-时间模型趋势项拟合的适用性。因此,选取传统西原蠕变模型为滑坡趋势项位移c(t)的拟合模型。

据文献[17]、文献[18],传统的西原蠕变模型方程为

(4)

式中:E0、E1分别为弹性模量与黏弹性模量;σ为总应力;σs为滑坡体屈服应力;e(t)为滑坡蠕变;η1、η2为黏滞系数。

据式(4),得到2条不同应力条件下的应变-时间(ε-t)曲线,如图1所示。

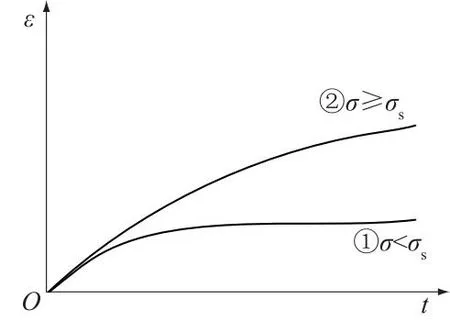
图1 不同应力条件下的蠕变曲线

考虑到滑坡位移处于不断累增状态,取滑坡位移-时间模型趋势项表达为变换参数后的西原模型关系式②,即

c(t)=a1(1-e-b1t)+c1t+D。

(5)

式中a1、b1、c1、D为趋势项位移待求解力学参数。

1.3 滑动Rnl检测

滑动Rnl检测是基于滑动t检验与滑坡蠕滑位移本构模型下的一种针对滑坡位移的新型突变检测方法。具体原理如下。

Rnl是基于直线回归拟合优度决定系数R2的曲线回归改进系数,作用在于判断曲线拟合的拟合优度。Rnl定义[19]为

根据最小二乘拟合规则,对滑坡水平位移5组以上数据进行逐点拟合。按照图1曲线②模式,控制c(t)参数的取值范围,保留大范围阶跃后线性的存在可能。

根据Rnl定义式,阶跃式位移产生之前,由于波动项的存在,Rnl表现为小范围波动;阶跃项位移产生时,突变点产生,最小二乘下的拟合函数在控制范围内无法收敛至突变点,使得Rnl有明显的下降趋势;阶跃项位移消失时,由于突变消失,滑坡位移继续向原趋势发展,Rnl有一定的上升趋势,并最终变为波动状态。

1.4 自适应改进遗传算法模型

曲线回归最小二乘拟合大多数采用的是Newton迭代法,即选取参数的初值,运用Newton迭代式将其迭代至理想精度范围内,完成求解。因此,对大范围参数初值进行搜寻,进而得到最优拟合曲线是保证滑动Rnl检测顺利进行的必要操作。本文选用自适应改进遗传算法模型进行Rnl最优值的求解。

遗传算法(Genetic Algorithm,GA)是一种智能算法,该算法把需要求解的优化问题模拟为一个生物自然进化过程,经过不断地迭代更新,最终找到一个最优解[20-21]。遗传算法可以直接进行搜寻求解计算,没有求导或连续性的界定,其运算的随机搜索性使其具有良好的全局寻优能力[22]。

本文运用遗传算法寻优的次数较多,寻优难度也有区别。因此,为了提高遗传算法效率,建立自适应改进遗传算法模型,如下:

设置自适应改进遗传算法选择模型,即

(7)

式中:p为被选择的个体;pfitness_max为种群中的最大适应度;pfitness_ j为当前个体适应度;j为当前累计个体数;i为当前累计数据个数;q为Rnl开始有大幅度下降趋势时的当前累计数据个数。

设置自适应改进遗传算法交叉与变异算子,即

(8)

式中:NPC、NMU分别为交叉算子与变异算子;NPC_cloud、NMU_cloud分别为云模式(cloud)下的自适应交叉算子与变异算子。

(1)产生大阶跃变形前,滑坡位移按蠕滑趋势进行发展,非线性拟合较为明显,遗传算法寻优困难。因此,设定选择模型为轮盘赌选择模型[23]并依据文献[24]改进轮盘赌适应度模型;同时,设定云模式[25]下的自适应交叉算子与变异算子,设定方式依据文献[26]。

(2)产生大阶跃变形后,滑坡位移趋势状态被打破,拟合曲线可能会呈线性或者类线性形态,遗传算法寻优较为简单。因此,设定选择模型为精英选择模型;同时,设置交叉、变异模型为传统单点交叉、变异模型,并设置交叉算子与变异算子为常用固定值0.9与0.1。

1.5 改进移动平均法剔除阶跃项

滑坡位移呈递增趋势发展,因此,阶跃项位移直接进行剔除会导致后续数据无法处理。提出一种基于移动平均原理的阶跃项位移剔除方法,具体如下:

考虑到加权移动平均法有观察期的近期观察值对预测值有较大影响的特征,应用加权移动平均法改进式进行阶跃项位移的剔除。

传统加权移动平均法适用于平稳时序,对于非线性递增时序无法应用,故做适当改进,即

(9)

wL-i=L-i。

(10)

依据加权移动平均原理,保留接近阶跃项的前5个权重,令

wL-6=wL-7=…=wL-n=0 。

(11)

综上,式(9)可简化为

(12)

阶跃点剔除并重新设置后,阶跃项位移为

m(L)=F(L)-mL。

(13)

式中:m(L)为L处剔除的阶跃项位移;F(L)为L处的滑坡总位移。

重置阶跃项后续位移数据,即

F(L+e)1=F(L+e)-m(L) 。

(14)

式中:F(L+e)1为L+e处的重置位移;F(L+e)为L+e处的原滑坡总位移;e=1,2,…,u,u为下个识别阶跃点的前一项。

2 白水河滑坡实例分析

2.1 白水河滑坡地质概况

白水河滑坡位于湖北省宜昌市三峡库区秭归县,该滑坡体前缘高程70 m,后缘高程390 m,南北长780 m,东西宽700 m,总体积1 260万m3,坡体地层岩性为侏罗纪中厚层状砂岩夹薄层状泥岩,产状为15°∠36°[27]。本文以ZG118监测点2003年6月—2008年8月的滑坡累计水平位移监测数据作为实例进行时序分解。ZG118监测点累计水平位移曲线如图2所示。

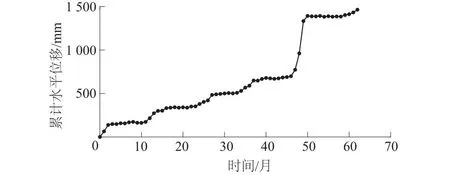
图2 ZG118监测点水平位移

据图2,ZG118累计水平位移曲线表现为明显的阶跃递增形态。

2.2 滑坡位移阶跃点识别

滑坡位移-时间趋势项表达见式(5),根据西原蠕变表达式,对式(5)中待求解参数进行初值搜索范围的约束。各参数搜索取值范围为

(15)

根据自适应改进遗传算法模型,得到滑动Rnl检测方法下的Rnl变化曲线,如图3。

图3 滑动Rnl检测

据图3,将Rnl降低的点作为阶跃点,得到滑坡位移突变点分布,如图4所示。

图4 滑坡位移突变点分布

根据突变点分布,由于突变幅度较大,产生了部分识别错误点,对识别错误点51、52、53进行剔除。剔除的突变点Rnl降低,为保证拟合性能,仍对剔除突变点进行改进移动平均修正。

2.3 滑坡位移时序分解

根据改进移动平均法剔除识别的阶跃点,修正阶跃数据与后续位移数据。对剔除阶跃点并修正后的位移数据做西原蠕变趋势项拟合,将拟合曲线作为趋势项位移曲线,拟合误差曲线作为波动位移曲线,剔除的阶跃曲线作为阶跃项位移曲线。得到时序分解后的滑坡位移表达式如下:

据总位移表达式(式(1)),趋势项位移、阶跃项位移、波动项位移表达式分别为:

c(t)=127.4(1-e-1.095t)+4.685t-4.025; (16)

(17)

w(t)=F(t)-m(t)-c(t) 。

(18)

滑坡位移时序分解后的趋势项位移曲线、波动项位移曲线、阶跃项位移曲线如图5所示。

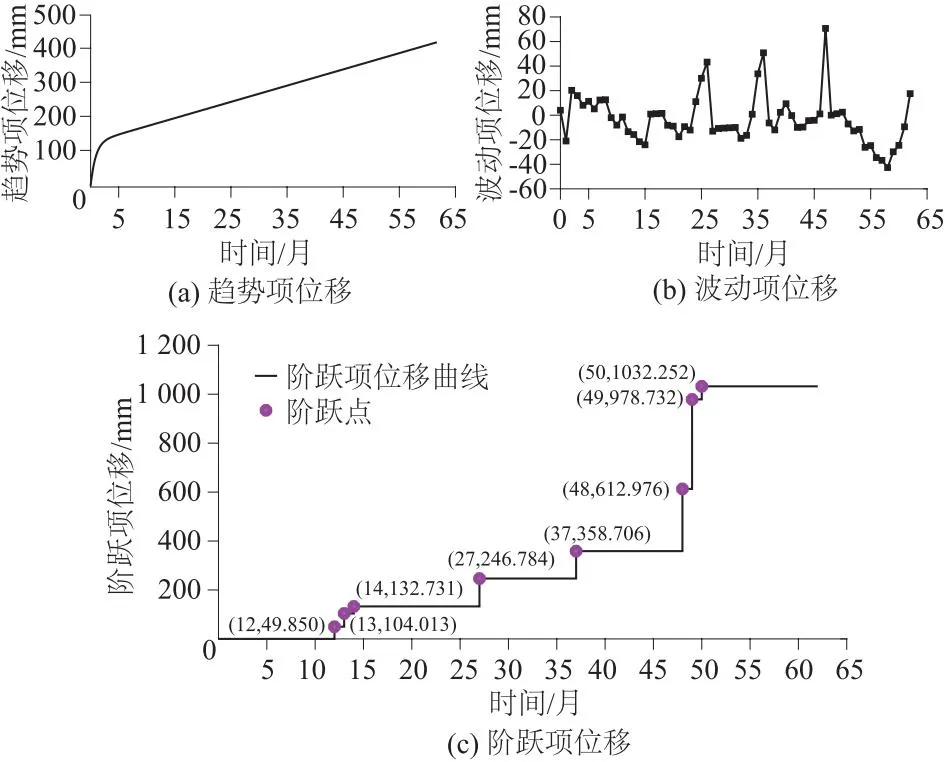
图5 时序分解后各位移曲线

滑坡总位移时序分解后的分解效果如图6所示。

图6 滑坡总位移分解效果

2.4 不同阶跃点检测方法对比分析

经典突变检测方法主要有:MK(Mann-Kendall)突变检测方法、滑动t检验突变检测方法、BG算法突变检验方法、pettitt突变检测方法以及Bayes突变检测方法等。其中,MK突变检测方法、滑动t检验突变检测方法、pettitt突变检测方法以及Bayes突变检测方法最为常用。

由于MK突变检测方法与pettitt突变检测方法检测原理类似,因此,本文选用MK突变检测方法、滑动t检验突变检测方法、Bayes突变检测方法与滑动Rnl检测方法做对比分析。突变检测结果如图7所示。

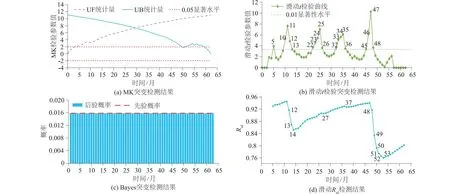
图7 突变检测结果

根据图7,MK突变检测结果表明,滑坡位移有很强的单调递增趋势,只检验出其具有趋势性,无法检测到突变点;滑动t检验检测出的突变点存在有明显且较多平稳序列,检测局部正确;Bayes突变检测结果表明,滑坡位移突变点产生概率均相等,无法识别特殊突变点。相较于上述方法,对于滑坡位移而言,滑动Rnl突变检测方法更加适用。

2.5 不同时序分解方法对比分析

现阶段较为常用的时序分解方法有移动平均法,指数平滑法、VMD方法、多项式最小二乘分解法等。由于多项式最小二乘分解较为简单,且数据量有限,本文选用二次移动平均法、三次指数平滑法、VMD分解方法与滑动Rnl检测时序分解方法做对比。

选取前5个数据作为一次移动平均计算数据,一次移动平均前5个数据作为二次移动平均计算数据;为保证指数平滑分解后曲线平滑性,指数平滑系数α定为0.3。VMD分解时不对分解后的模态个数k进行讨论,采用传统分解方法,分解出的波动曲线集合作为波动项位移曲线。白水河滑坡二次移动平均分解、VMD时序分解、三次指数平滑分解以及新型时序分解结果如图8所示。

图8 时序分解结果

根据图8可知:

(1)二次移动平均法时序分解后丢失了一部分原始数据,对后续的时序预测会造成一定的影响;分解出的趋势项位移无规律性,也没有力学理论支撑,可能会造成由强降雨、库水位急剧变动或者偶然因素引起的非趋势项位移也计算在趋势项位移内;分解后的波动项位移变化幅度较大,预测的误差可能会超出允许误差范围;由于处理后趋势项数据分布仍不规则,三次多项式拟合的效果也较差,均方根误差RMSE为59.07 mm,且拟合曲线发展趋势与原始数据发展趋势也不相同。二次移动平均趋势项拟合曲线如图9所示。

图9 二次移动平均趋势项拟合曲线

(2)三次指数平滑法时序分解后同样有无规律性,将非趋势项位移计算在趋势项位移内的可能;分解后的波动项位移变化幅度仍然较大;三次多项式拟合的效果相较二次移动平均法好,但均方根误差RMSE仍有34.14 mm,且拟合曲线发展趋势与原始数据发展趋势不同的问题仍然存在。三次指数平滑趋势项拟合曲线如图10所示。

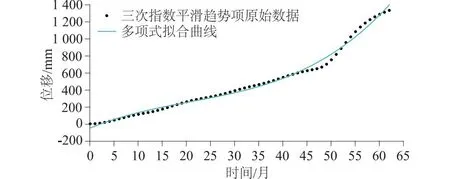
图10 三次指数平滑趋势项拟合曲线

(3)相较于前2种时序分解方法,VMD时序分解也存在趋势项无规律性等问题。同时,趋势项位移前期出现了大量负值,与实际现象不符。此方法并不适用。

综上并结合图8(d)可知,滑动Rnl检测时序分解方法有如下优势:①解决了趋势项位移无规律、无力学依据的问题; ②分解后的趋势项位移无负值;③波动项位移变化幅度较小,预测精度有所提高;④西原蠕变模型拟合效果较好,均方根误差RMSE为18.56 mm,发展趋势具有递增性且符合力学规律;⑤引入“阶跃式”滑坡位移预测中最重要的阶跃项位移,分析预测更具有针对性。