小断面土石组合地质条件下TBM施工围岩可掘性分级识别

杨耀红,刘德福, 张智晓, 韩兴忠, 孙小虎,4

(1.华北水利水电大学 水利学院,郑州 450046; 2.河南省黄河流域水资源节约集约利用重点实验室,郑州 450046;3.中州水务控股有限公司, 郑州 450000; 4.中水北方勘测设计研究有限责任公司,天津 300000)

0 引 言

土石组合体是指由岩体和土体组合而成的开挖断面,即土石分界线切割开挖断面的情况,它不同于既含有土又含有岩石的土石混合体[1]。隧道掘进机(Tunnel Boring Machine,TBM)施工过程中遇到这一复杂地质条件,需要采用适当的TBM掘进参数;若TBM掘进参数与地质条件不匹配,TBM掘进效率会降低,造成工期延长和成本增加。特别是对于小洞径隧洞,由于TBM机身较小较轻,一方面若掘进推力小、刀盘转矩小且贯入度小,掘进效率不高;另一方面若掘进推力大、刀盘转矩大且贯入度大,会造成TBM机身轴线偏离度大,需要不断纠偏,掘进效率也不高。因此在此复杂地质条件下,传统的围岩分级方法已不适用,需要确定新的适合TBM施工需要的围岩分级,并对围岩分级精准识别,也是TBM设备智能控制并最终实现无人驾驶的必然要求。

目前,国内外许多学者提出了TBM施工围岩分级标准。何发亮等[2]结合安康铁路秦岭TBM施工隧道,基于岩性参数建立了围岩分级标准。张宁等[3]以传统围岩分类方法为基础,依据岩石单轴抗压强度等指标,探讨了围岩分级的标准。闫长斌等[4]结合国内某工程,基于改进距离判别分析法建立了TBM施工围岩分级标准。李春明等[5]基于BQ(Basic Quality)法构建了围岩分级标准。王攀等[6]利用岩性参数和掘进参数对围岩进行分级。但这些研究很少涉及小断面土石组合地质条件下TBM施工围岩分级问题。

此外,TBM施工围岩等级识别也是保证TBM施工效率的重要问题,国内外学者也做了大量研究[7-10],尤其是近些年来,大量学者采用机器学习方法进行识别研究。Yang等[11]基于现场掘进的岩渣等地质参数,利用卷积神经网络(Convolutional Neural Networks,CNN)模型对TBM施工围岩进行了分类识别。Hou等[12]结合松花江输水工程,利用大数据和集成学习算法对TBM施工岩体进行分类识别预测。毛奕喆等[13]基于岩体信息和掘进参数,采用机器学习算法对TBM围岩进行实时识别和预测。段志伟等[14]基于主成分分析-反向传播(Principal Components Analysis-Back Propagation, PCA-BP)算法对TBM围岩进行实时识别和预测。杜立杰等[15]基于施工现场数据对TBM可掘性进行实时识别预测。Liu等[16]基于TBM施工数据,利用长短期记忆(Long Short-Term Memory,LSTM)模型对隧道岩性进行识别预测。Zhang等[17]利用K-means算法搜索TBM潜在的围岩类型,并且利用了支持向量机对TBM围岩进行了实时识别。Liu等[18]提出了分类回归树与AdaBoost算法相结合的集成学习模型,并用该模型对围岩的分类进行了预测,并且与其他机器学习模型进行了对比。但这些机器学习模型对TBM施工围岩可掘性识别的适用范围尚待进一步检验,且识别精度尚需进一步提高。

主成分分析(Principal Components Analysis,PCA)可以减少原始变量的维度并且不会丢失原始变量大多数信息,以此来简化模型的输入。随机森林(Random Forests,RF)模型具有非常强大的非线性分类能力。目前,PCA-RF组合模型已经运用到很多领域,例如岩性质量分类[19]、PM2.5预测[20]、体育运动分类[21]等。基于此,本文结合南水北调安阳市西部调水工程,对TBM施工过程中提取的掘进性能参数进行数据分析,在传统围岩分级的基础上,引入了2个综合性能指标FPI(现场贯入指标)、TPI(扭矩贯入指标),建立了新的围岩可掘性分级标准,提出了PCA-RF模型,并用该模型对TBM施工围岩可掘性分级进行识别。本文建立的TBM施工围岩分级标准更贴合工程实际,识别模型有更高的准确率,可以更好地指导TBM施工。

1 工程概况

南水北调安阳市西部调水工程,全长13.18 km。隧洞工程主要包括TBM掘进段、钻爆段等,其中TBM掘进段长为11 822 m,比降为0.01%,采用圆形断面,开挖直径为4.33 m,设计断面直径为3.5 m,在TBM施工开挖断面中,属于小断面开挖。TBM整机长约为275 m,主机长约为12 m,主要的TBM性能参数如表1所示,图1为隧洞地质剖面。

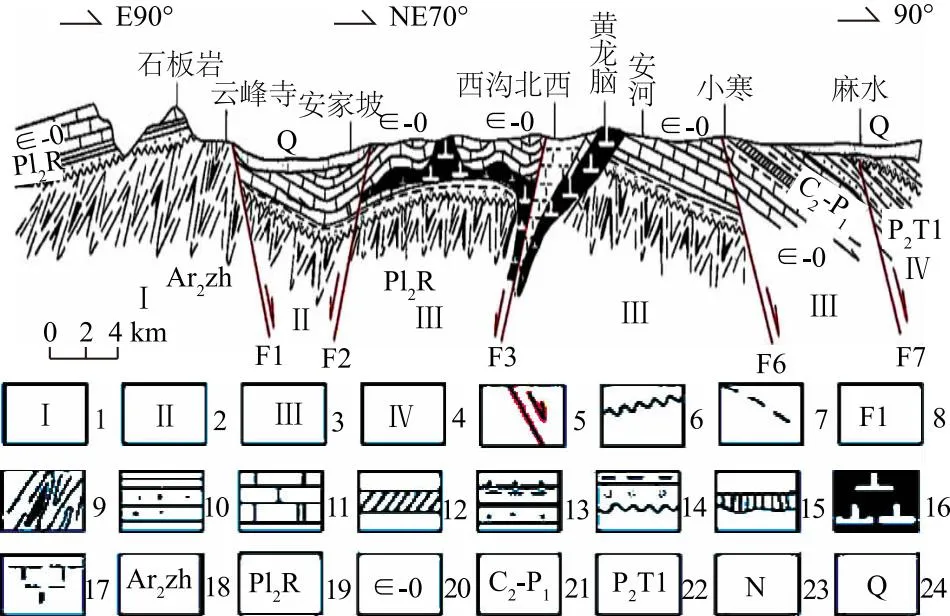
注:1.云峰寺基底隆起,2.林县地堑式断陷盆地,3.黄龙脑-马鞍山地垒式断隆,4.水冶向斜式断陷盆地,5.北北东向深断裂,6.不整合界限,7.平行不整合界线,8.断裂编号,9.赞皇群结晶基底变质杂岩,10.含砾石英岩状砂岩、页岩,11.白云质灰岩、灰岩,12.本溪组铁、铝层,13.砂岩、泥岩夹煤层,14.砾岩、黏土岩,15.冲、洪、残、坡积沉积岩,16.闪长岩,17.正长岩,18.新太古界赞皇群,19.中元古界蓟县系- 汝阳群,20.寒武-奥陶系,21.上石炭统下二叠统,22.中二叠统-下三叠统,23.新近系,24. 第四系。

表1 TBM主要技术参数

工程地质勘察报告和设计图纸显示,隧洞全部在岩石体中,围岩主要有石灰岩、泥岩、闪长玢岩等,传统的分级方法将围岩分为Ⅲ、Ⅳ、Ⅴ类。其中Ⅲ类围岩地段占39.6%,Ⅳ类围岩地段占24.3%,Ⅴ类围岩地段约占36.1%。工程施工过程中,开挖掌子面出现了土石组合情况,如图2所示,掌子面左右部为黄色黏性泥土,其余为灰色、灰褐色石灰岩、局部夹薄层白云质灰岩、角砾状灰岩。

图2 开挖掌子面

2 TBM施工围岩可掘性分级

2.1 各级围岩下的TBM掘进参数对比

选取TBM掘进段桩号为18+896—30+718的典型土石组合洞段进行数据收集以及分析。传统的分级方法将本标段内的围岩等级分为Ⅲ、Ⅳ、Ⅴ类。由于本工程出现了典型碳质泥岩洞段,且传统的围岩分类不足以使TBM设备在此类围岩有效掘进。因此,本文依据新的围岩分类标准重新划分。将Ⅲ类围岩细分为ⅢA类、ⅢB类围岩,与碳质泥岩洞段、Ⅳ类、Ⅴ类围岩一起进行分析讨论,保证TBM设备高效率、稳定地掘进。依次收集各类围岩TBM掘进性能参数进行数据分析,获取影响可掘进分级的指标。

2.1.1 各级围岩下TBM平均贯入度与净掘进速度

各级围岩下TBM的平均净掘进速度与平均贯入度对比如图3所示。

图3 各级围岩下的TBM平均净掘进速度、平均贯入度

从图3可以看出,TBM在Ⅳ、ⅢA类围岩净掘进速度最高,ⅢB、Ⅴ类围岩次之,泥岩段净掘进速度最低;TBM在泥岩段、ⅢA类围岩下贯入度最高,ⅢB、Ⅳ类围岩次之,Ⅴ类围岩贯入度最低。

2.1.2 各级围岩下TBM平均施工速度与平均刀盘转速

各级围岩下TBM的平均施工速度与平均刀盘转速对比如图4所示。

图4 各级围岩下的TBM平均施工速度、平均刀盘转速

从图4可以看出,TBM在ⅢA类围岩下施工速度最高,ⅢB、Ⅳ类围岩次之,泥岩段及V类围岩下最低;TBM在ⅢA类围岩下刀盘转速最高,ⅢB、Ⅳ围岩次之,泥岩段及V类围岩下最低。

综合分析图3和图4,如果以净掘进速度作为围岩分级指标,则Ⅳ类围岩为适合TBM掘进段,其TBM净掘进速度最高,但是其施工速度较低,并且Ⅳ类围岩下刀盘转速也相对最低,TBM总体在Ⅳ类围岩下适应性不高,掘进效率较低。如果用贯入度作为围岩分级指标,则泥岩段为最适合TBM掘进段,其贯入度最高,而相对应的施工速度和转速最低,表明TBM在泥岩段掘进效率较差,不适宜掘进,易产生围岩坍塌、卡机等事故。所以净掘进速度、贯入度等指标不适合作为围岩可掘进性的分级指标。

2.1.3 各类围岩下TBM可掘进指标FPI和TPI

为了消除TBM土石组合围岩下掘进性能自身的影响,引入更能表征围岩分级标准的综合性指标FPI(单位贯入度推力,见式(1))和TPI(单位贯入度扭矩,见式(2))。各级围岩下的FPI和TPI如图5所示。

(1)

图5 各级围岩下TBM的FPI、TPI

(2)

式中:Fn为刀盘总推力(kN);Tn为刀盘扭矩(kN·m);P为刀盘贯入度(mm/r)。

从图5可以看出,FPI和TPI在ⅢA类围岩下最高,ⅢB、Ⅳ类围岩次之,泥岩段和Ⅴ类围岩下最低,表明TBM在ⅢA类围岩贯入度为1 mm/r时所需的推力和扭矩最大,在Ⅴ类围岩贯入度为1 mm/r时所需的推力和扭矩最小。并且FPI、TPI在各类围岩下具有很好的区分度,但是可以看出ⅢB类围岩和Ⅳ类围岩下的FPI与TPI相差较小,且从表2可以看出ⅢB类围岩和Ⅳ类围岩下的掘进参数相差也较小,因此本文将ⅢB类围岩和Ⅳ类围岩归为同一性质的围岩。综合分析各个围岩段TBM的掘进性能以及现场掘进情况,选定FPI、TPI作为TBM施工围岩可掘性分级的指标是适合的。

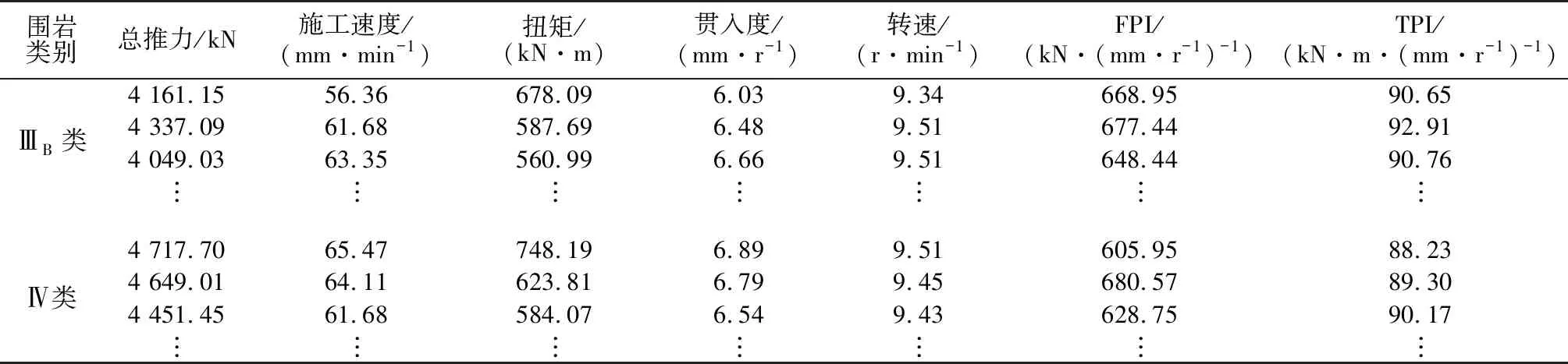
表2 ⅢB级围岩和Ⅳ级围岩下的TBM掘进参数对比

2.2 围岩可掘性分级

在施工现场采取的数据发现,在一些ⅢB类围岩和Ⅳ类围岩下的TBM掘进性能参数相近,如表2所示。

从表2可知,一些完整性较好的Ⅳ类围岩和ⅢB类围岩下TBM掘进参数相差很小,掘进效率几乎相同。本文 ⅢB类围岩指的是FPI 为700～600 kN/(mm/r) 之间,且TPI集中在100～80 kN·m/(mm/r)。

结合现场施工情况并根据传统分级方法,ⅢA类围岩施工速度与刀盘转速均为最高,且岩体大部分完整。虽然ⅢA类围岩有较高的单轴抗压强度,但是围岩局部较稳定,不需做大量的支护工作,并且TBM在ⅢA类围岩总推力和刀盘扭矩最高,所以贯入度也相对较高。因此,TBM在ⅢA类围岩掘进效率最好,适应性较强,所以隧洞采用TBM施工适宜性基本定义为A类(适宜施工)。ⅢA类围岩指的是FPI≥700 kN/(mm/r)、TPI≥100 kN·m/(mm/r)。

结合现场施工情况并根据传统分级方法,ⅢB、Ⅳ类围岩掘进效率仅次于ⅢA类围岩,但是相对于ⅢA类围岩,施工速度和刀盘转速有所下降,施工风险有所增加。所以隧洞采用TBM施工适宜性为B类(基本适宜)。考虑到ⅢB、Ⅳ类围岩的掘进性能参数相差较小,将ⅢB、Ⅳ类围岩归为同一类性质的围岩。

结合现场施工情况并根据传统分级方法,泥岩段岩体完整性差,围岩不稳定,施工速度与刀盘转速最小,但是也有相对较好的贯入度,并且TBM总推力和刀盘转矩也相对良好,所以泥岩段围岩隧洞采用TBM施工适宜性为C类(不适宜)。泥岩段的FPI和TPI大多数分别集中于500～400 kN/(mm/r)和80～50 kN· m/(mm/r)。

结合现场施工情况并根据传统分级方法,Ⅴ类围岩完整性最差,局部最不稳定,最容易发生刀盘卡机、围岩坍塌等事故,且施工速度与刀盘转速较小,需要大量的围岩支护工作才能有效地掘进。所以隧洞采用TBM施工适宜性为D类(特别不适宜)。

综合以上分析,利用可掘性综合指标FPI和TPI,将FPI≥700 kN/(mm/r)、TPI≥100 kN·m/(mm/r)的围岩定义为A类,将FPI为700～600 kN/(mm/r)、TPI为100～80 kN· m/(mm/r)的围岩定义为B类,将FPI为500～400 kN/(mm/r)、TPI为80～50 kN· m/(mm/r)的围岩定义为C类,将FPI<400 kN/(mm/r)、TPI<50 kN·m/(mm/r)的围岩定义为D类。如表3所示。

表3 TBM围岩可掘性分级

由表3所知,利用FPI和TPI指标重新进行围岩分级,解决了传统围岩分类无法处理土石组合围岩的难题,并很好地改善了ⅢB类和泥岩段围岩实际施工应用的局限性。结合TBM实际掘进效率来看,利用FPI和TPI这2个综合指标来重新进行围岩可掘性分级更加贴近实际施工状况。

3 围岩分级识别模型

3.1 主成分分析

主成分分析(PCA)[22-23]是一种简化数据集的技术。它可以通过减少维度来压缩数据,并且数据不会有太多的丢失,同时可以保留原始数据集中存在的内部原始数据信息。主成分分析由以下步骤组成:

假设一个数据集有n个样本,每个样本由p维向量表示,即x1,x2,…,xp。因此,原始数据矩阵可以表示为X=(X1,X2,…,Xp)=(xij)n×p。

(1)为了消除不同维度的影响,需要对原始变量进行标准化,见式(3)。然后计算协方差矩阵,即标准化矩阵的相关系数矩阵,因为标准化之后的变量相关系数矩阵是不变的。

(3)

式中:xij为n组p维的数据样本矩阵数据;xkj为第k行第j列的样本数据;yij为标准化之后的数据样本矩阵数据。

(2)计算矩阵特征值和相应的正交化单位特征向量。然后根据累积贡献率提取m个主成分。最后算出相对应的主成分得分代入模型进行识别。

3.2 随机森林模型

随机森林(RF)[21,23-25]是一种综合学习方法,它主要使用bagging方法和简单的决策树概念,并使用自抽样技术和一种分类回归树(SA)算法生产多个不相关的决策树。

然后,结合这些决策树的结果来提高泛化性能。随机森林大致计算过程如下:

(1)假设N是原始数据集D的学习样本的大小。Bootstrap采样用于从原始数据(N个CART(分类树))生成N个不同的训练样本数据集。

(2)每个决策树t在不同的Bootstrap样本Dt上生长,其中包含用于替换训练样本Nn随机选择样本。在t的每个节点,如果每个样本的特征维度为L,指定一个常数p≪L,随机地从L个特征中选取p个特征子集,每次树进行分裂时,从这p个特征中选择最优的。

(3)每个决策树t使用CART树算法增长到最大值。

(4)要对新样本进行分类或者预测,将输入向量置于n个树下。每棵树都为预测的类别投票。最后的结果是通过n个CART类别的多数投票获得的。

为充分发挥RF模型强大的非线性分类能力,克服传统分类方法的局限性,本文采用PCA-RF组合模型对围岩可掘性进行分类识别。通过PCA降维求解得到能够反映绝大多数信息的主成分,以此减少RF模型的输入,加快模型训练速度,提高模型识别精度。然后利用RF模型对围岩可掘性进行分类,弥补传统决策树分类方法过于复杂、识别度不高等缺陷。组合模型计算流程如图6。

图6 PCA-RF模型流程

4 工程应用分析

4.1 TBM参数主成分分析

基于上述讨论,依次选取A、B、C、D类围岩典型洞段各50组数据,共200组数据。表4为所选取的样本数据统计。

表4 样本数据统计

为了消除量纲以及多重维度的影响,需要对原始数据进行标准化处理,按照式(3)进行计算。运用SPSS软件对标准化后的数据进行主成分分析。表5为主成分特征值与累积贡献率。

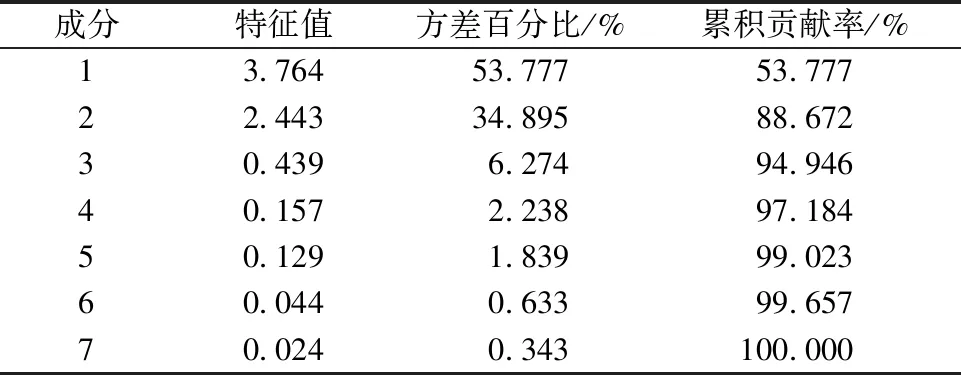
表5 主成分特征值与累积贡献率

主成分个数提取原则主要包括2个标准,第一个是主成分对应的特征值>1的前m个成分,第二个是前m个主成分累积贡献率>85%。从表5可知,主成分1和主成分2的特征值>1,且累计贡献率也已经达到了88%,可以认为前2个主成分包含了原始数据的绝大多数信息。所以本文只提取主成分1和主成分2。

表6为经过SPSS运算后所得到各个主成分得分系数矩阵。

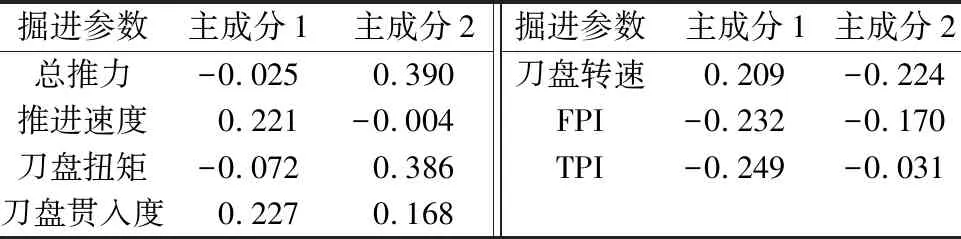
表6 主成分得分系数矩阵

将得分系数矩阵、特征值和标准化后的原始矩阵数据进行计算可以得到相应的主成分得分。表7为前2个主成分得分。

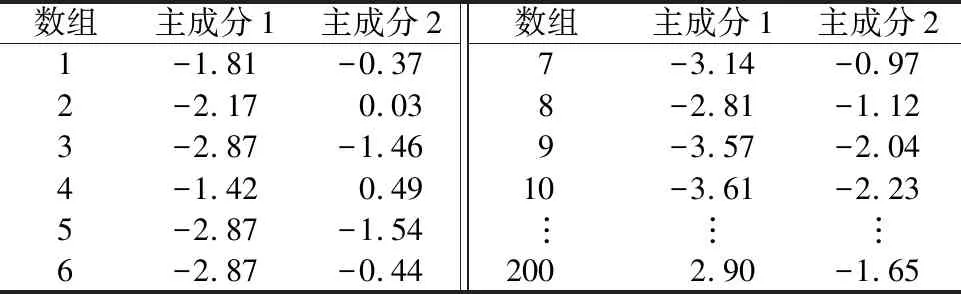
表7 前2个主成分得分

4.2 PCA-RF模型识别

因为RF模型自身的优势,模型本身可以处理异常值,并且根据自己的特征进行缩放,无需再进行数据预处理。

基于MATLAB2020b的实验环境,随机抽取主成分1、主成分2 的30%为测试集,剩下的70%为训练集,经过不断地对模型参数调试,决定采用30次HoldOut函数交叉验证,随机树为200,每棵树的输入变量为2,模型最终达到目标要求的最好的识别准确率。

采用识别准确率(metrics score,ms)来评价随机森林模型对掘进参数分类识别,见式(4)。表8为PCA-RF组合模型对各类围岩的识别结果。

(4)

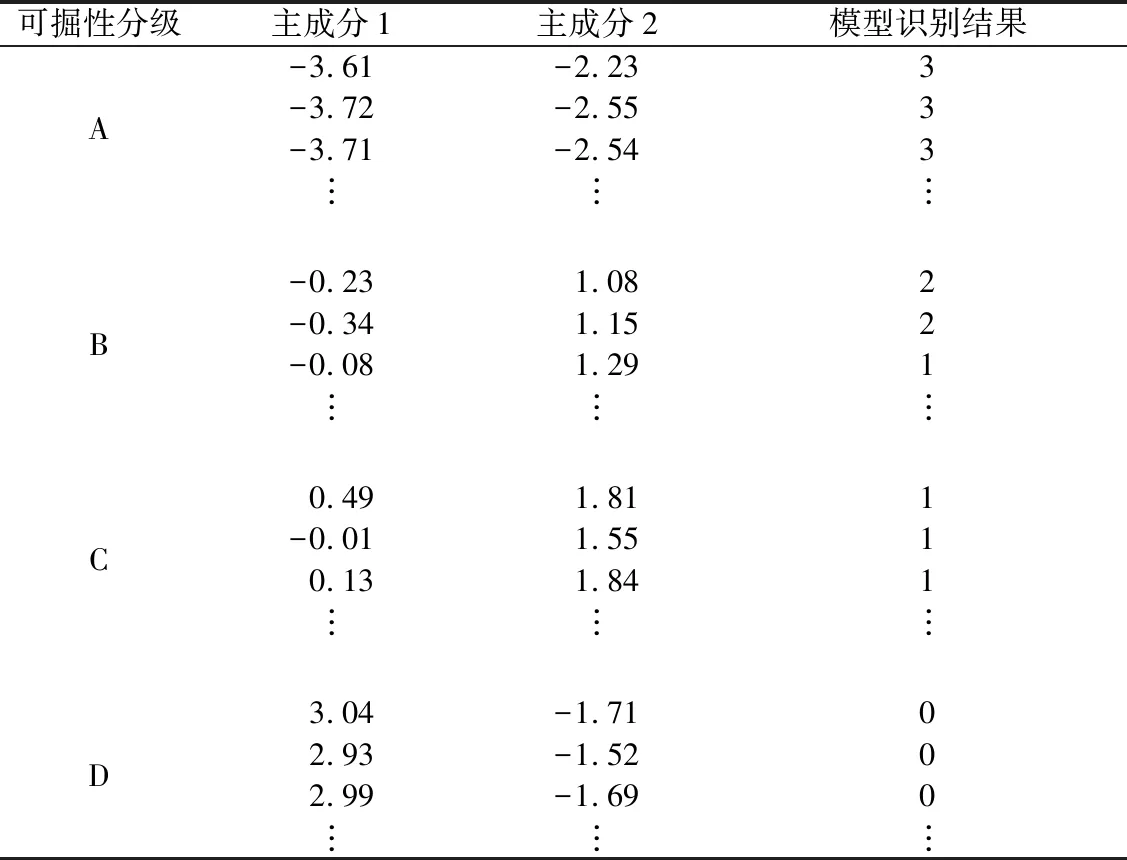
表8 PCA-RF组合模型识别结果

由表8可知,PCA-RF模型对60组不同类型围岩的识别率达到了100%,仅有B类围岩中有一组数据识别错误,识别准确率达到了98.3%。综合分析,通过PCA算法对不同类型围岩下的掘进数据进行降维处理,抵消了各掘进参数之间的相关性,不仅缩小了RF模型输入的维度,也提高了模型的识别速度,模型得到了良好的识别准确率。

4.3 分析讨论

为了进一步体现PCA-RF模型适应性更好,将其与BP、SVR(Support Vector Regression)和RF模型进行对比分析。通过与没有进行PCA算法的各个围岩下掘进参数识别精度进行对比。依次选取A、B、C及D类围岩各50组数据作为BP、SVR和RF模型的输入,RF模型的参数不发生改变,BP模型具体参数:隐含层为6,最大迭代次数为1 000,目标训练误差为10-6,学习率为0.01。SVR具体参数:惩罚因子为10.0,径向基函数为0.01,损失函数p值为0.1。测试集和训练集不发生改变,与RF模型保持一致。表9为RF模型对各类围岩的识别结果。

表9 RF模型识别结果

由表9可知,RF模型对60组不同类型围岩下没有经过PCA降维掘进参数识别率也达到了100%,共有A类及B类围岩中5处识别错误,识别准确率只有91.6%。BP和SVR的识别准确率为93.3%。由此可以看出PCA-RF模型要优于上述模型,识别准确率更高。

5 结 论

本文针对南水北调安阳市西部调水工程小断面土石组合TBM施工围岩分级问题,采用FPI、TPI两个综合性能指标,建立了新的围岩可掘性分级标准,并提出了TBM施工围岩分级PCA-RF识别模型,基于工程实际数据进行了计算验证,并与BP、SVR和RF模型进行了对比分析,结果表明:

(1)针对小断面土石组合TBM施工围岩,在传统围岩分类的基础上,结合FPI、TPI指标建立的小断面土石组合围岩TBM施工可掘性分级标准,克服了土石组合围岩下传统围岩分类方法的局限性,更加贴合工程实际应用,可为后续工程施工提供参考。

(2)采用小断面土石组合TBM施工围岩分级识别的PCA-RF模型,对围岩可掘性分级进行了识别,识别率达到了100%,识别准确率达到了98.3%。与BP、SVR和RF模型进行对比发现,PCA-RF模型的识别准确率要高于BP、SVR和RF模型,体现了PCA-RF模型的适用性较强。

(3)本文的局限性在于,选取的工程实例只有一个型号的TBM设备,工程中围岩等级以及土石组合类型也较少,所以对围岩分级标准适用性以及模型识别准确率的检验还不充分。后续研究可针对更多型号的TBM设备,获取更多围岩类型的施工数据,对围岩分级标准适用性以及模型识别准确率进行充分检验,以更好地指导TBM施工。