后量子时代区块链中哈希函数比较研究
2024-03-12许盛伟秦晓宏蓝浩书
刘 昂 文 津 许盛伟 陈 颖 秦晓宏 蓝浩书
1(北京电子科技学院网络信息化管理处 北京 100070)
2(北京邮电大学网络空间安全学院 北京 100876)
3(北京电子科技学院网络空间安全系 北京 100070)
4(北京电子科技学院信息安全研究所 北京 100070)
5(北京电子科技学院密码科学与技术系 北京 100070)
2008年,Nakamoto[1](中本聪)首次引出了区块链的概念.此后,区块链技术得到全世界学者的深入研究,并在各行各业得到广泛应用.
我国非常重视区块链的发展,2016年,国务院首次将区块链技术作为战略性前沿技术列入《“十三五”国家信息化规划》[2];2019年10月24日,十九届中共中央政治局就区块链技术发展现状和趋势进行第十八次集体学习,强调“把区块链作为核心技术自主创新重要突破口,加快推动区块链技术和产业创新发展”[3],区块链已被提升到国家战略高度;2021年两会后,区块链作为数字经济7个重点领域被写入十四五规划纲要[4],表明2021—2025年区块链已被列入政府重点工作内容.
区块链是一种链式数据结构[5],以区块(block)的形式存储数据,区块按照生成时间顺序组成1条链,1个区块中存在多笔交易信息,多个区块通过哈希值前后连接,形成一个“区块链”.
区块链从本质上讲是一个共享信息数据库[6],存储于其中的数据或信息具有“不可伪造”“不可篡改”“全程留痕”“可以追溯”“公开透明”“集体维护”等特征.基于这些特征,区块链技术奠定了坚实的“信任”基础,创造了可靠的“合作”机制,具有广阔的应用前景.
区块链在网络安全中扮演着至关重要的角色[7],可以降低可能导致整个网络故障的网络攻击风险.然而量子计算机以其强大的并行计算能力,可以轻松破解经典计算机难以破解的数学困难问题[8],从而对现代密码技术尤其是公钥密码构成安全威胁.量子计算对传统密码学的影响极大程度地威胁了区块链系统的安全稳定发展.Grover量子算法在搜索上较经典搜索算法能提供2次加速,从而能加速对哈希函数的前像碰撞攻击[9].量子计算机的大规模应用将对哈希函数的安全性造成巨大影响[10],进而给网络安全带来巨大隐患[11-12],所以研究具有抗量子性的哈希函数意义重大.
本文将首先研究量子计算机对区块链中的哈希函数的攻击形式,然后开展区块链中哈希函数的抗量子安全性研究,对当前区块链中的哈希函数的设计进行归纳和总结,最后对后量子时代区块链中的哈希函数的设计提出有益建议并对前景进行了展望.
1 哈希函数及其面临的量子计算攻击威胁
1.1 哈希函数定义及其性质
作为区块链的起源性技术,哈希函数在区块链的数据完整性保护上发挥着不可替代的作用,哈希函数的抗第二原像性(弱抗碰撞性)直接决定了区块链的不可篡改性[13].
哈希函数又称散列函数,是密码学上一类将任意长度的消息映射到某一固定长度的哈希值的单向函数,它满足以下3个基本性质[14]:
1) 抗原像性.对任意给定的哈希值h,寻找1个消息x,使得H(x)=h在计算上不可行.
2) 弱抗碰撞性.给定消息x,其哈希值h=H(x),寻找1个不同于消息x的消息x′,满足h=H(x′)在计算上不可行.
3) 强抗碰撞性.寻找2个不同的消息x和x′,使得H(x)=H(x′)在计算上不可行.
1953年,IBM公司提出,为提高对数据库文件的检索效率,为每个文件生成1个电子指纹,搜索文件时直接搜索其电子指纹就能将文件搜索出来,简单高效.1981年,为提升数字签名RSA的安全性,避免伪造攻击,防止数据被篡改,Davis和Price提出密码哈希函数的概念[15].数据被篡改后电子指纹发生变化,从而发现篡改行为,进而保证数字签名的安全性.对文件进行数字签名时,仅对其摘要值而非原文件进行签名即可,提升数字签名效率.摘要值长度从128b,160b,192b,256b,384b,…,512b不等,高效便捷.当前主流的基于公钥的数字签名,即运用哈希函数对文件生成定长的摘要值后进行数字签名.
1.2 针对哈希函数的量子计算攻击
哈希函数在区块链系统中应用广泛,以比特币平台为例,在交易中使用哈希函数对每一笔交易生成摘要值后作数字签名;在链上数据的完整性保护上,使用哈希函数及基于哈希函数的Merkle树结构作完整性校验,并使用哈希值完成前后区块的连接;在工作量证明(proof of work, PoW)共识机制中使用寻找哈希函数特定输出对应的输入作为数学难题来为矿工分配新区块的记账权.
以Grover算法为代表的量子算法能有效实施针对经典哈希函数的量子计算攻击,攻击形式主要是原像攻击和第二原像攻击.
1.2.1 挖矿攻击
原像攻击:在密码学中,哈希函数上的原像攻击用于寻找有着特定哈希值的消息,1个哈希函数应该抵御对其原像的攻击.即给定y,找到1个原像x,使得H(x)=y.在比特币中,矿工们通过寻找满足哈希值为特定值的NONCE来获得新区块记账权和挖矿奖励(新比特币的产生).比特币挖矿就是发现新区块、验证待确认交易并将其添加到比特币区块链的过程.量子攻击者使用Grover算法加速搜索,能很快找到原像,从而在挖矿游戏中取得压倒性优势,甚至垄断记账权,从而大大破坏比特币系统的去中心化程度,这就是针对PoW共识机制的挖矿攻击.该攻击将导致51%攻击,即拥有量子计算机的矿工能凭借压倒性的算力优势将垄断新区块的生成,破坏区块链的去中心化[16].
为提高对原像攻击的抗性,双重哈希是一种可以抵御在某种情况下攻击者已经破解了首个哈希的好策略.比特币系统使用双重哈希SHA-256,这是一种2000年代减缓哈希破解的常见手段[17].然而量子攻击者使用的是暴力破解手段,双重哈希结构并未改变像(输出)的空间大小,因而不能有效抵抗量子敌手的原像攻击.
1.2.2 伪造攻击
第二原像攻击:攻击者在哈希值维持不变的前提条件下找到假消息m′替换合法消息m,即寻找m′使得H(m′)=H(m).在比特币为代表的区块链系统中,攻击者通过寻找哈希冲突,对区块链上的数据实施第二原像攻击,使用非法数据篡改合法交易数据,并且由于哈希值维持不变,也不会被校验发现.这就是针对链上数据的伪造(篡改)攻击.
哈希函数是把任意长度的输入(又叫作预映射(pre-image))通过哈希算法变换成固定长度的哈希值输出,因此这种转换是一种压缩映射,即哈希值的空间通常远小于输入的空间,不同的输入可能会哈希成相同的输出,因而从映射角度看,哈希函数显然是多对1映射,因此理论上必然存在碰撞,这也正是量子敌手成功实施第二原像攻击的基础,但是并非所有的消息都有第二原像.
近年来,大量研究量子计算机的机构和学者利用量子力学现象解决常规计算机难以解决的数学困难性问题.2019年,Google团队就在1台53b的量子计算机上仅用200s便完成了在超级计算机上需要1万年的计算[18],显示了量子计算超强的运算速度与处理能力,也透露出量子技术对区块链的潜在威胁.有研究显示,Bitcoin,Ethereum,Dash,Litecoin,Zcash,Monero,Ripple,NXT,Byteball,Bytecoin,IOTA等区块链均已受到量子威胁影响[19].而哈希函数在区块链中扮演重要角色,被王小云院士视为区块链的起源性技术.哈希函数在区块链中具有加密数据、验证数据、身份认证等重要功能,区块链数据的不可篡改等特性就是哈希函数的抗碰撞性确保的.如果大型量子计算机被完全研发出来,它们将对当前的经典密码算法尤其公钥密码造成毁灭性的灾难,许多协议、算法将不再是安全的[20].

量子敌手可以使用Grover算法通过搜索哈希冲突,在不改变哈希值的条件下篡改某一笔交易而不被发现.Grover的搜索算法[22]允许在计算逆哈希函数时实现2次加速效果,这种攻击将允许攻击者篡改链上的合法交易,破坏区块链上的数据完整性.例如,文献[23]使用Grover算法查找哈希函数中的冲突,得出哈希函数必须输出3n位才能提供n位安全级别的结论.这样的结论意味着许多当前的哈希函数在后量子时代将无效,而其他像SHA-2或SHA-3这样的函数将不得不增加其输出大小.
以使用Merkle树的比特币为例,量子敌手可以通过使用Grover算法构造数据,使得构造出的数据与真实数据通过同一个哈希函数计算出的值相同,以达到篡改数据并维持哈希值不变从而不被发现的目的.例如在图1的Merkle树中,敌手构造的数据Tx′与原始数据Tx通过同一哈希函数计算出的哈希值相同,即H(Tx)=H(Tx′),从而用Tx′替换原始数据Tx,其哈希值及Merkle根将维持不变,以实现前像碰撞攻击.
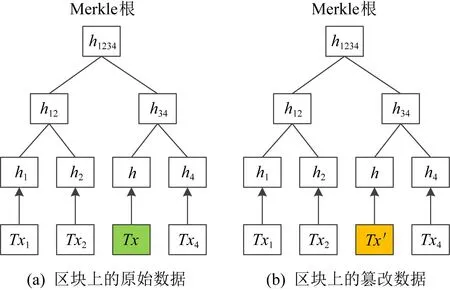
图1 前像碰撞攻击
2 哈希函数对比分析
本文对5种哈希算法进行了对比分析,其输入、输出、优点与缺点如表1所示:

表1 哈希算法总结
2.1 传统经典哈希算法
自1953年Hans Peter Luhn提出哈希函数[24]以来,1970年哈希函数蓬勃发展,2001年美国国家标准与技术研究院(National Institute of Standards and Technology, NIST)发布SHA-256算法[25],2008年中本聪[1]将哈希函数应用到区块链中,并成为区块链技术不可撼动的基石.
SHA-256算法属于SHA-2系列,在2008年被公认为最安全最先进的算法之一,中本聪提出的比特币除了生成地址中有一个环节使用了REPID-160算法,其他需要作哈希运算的地方均使用SHA-256,SHA-256是最早运用于区块链中的哈希函数之一.其他的传统经典哈希算法Ethash,Scrypt,RIPEMD160等,下面具体介绍SHA-256.
SHA-256[26]是一个Merkle-Damgard结构的迭代哈希函数,如图2所示,计算流程是一个迭代计算的过程,当最后一个消息块处理完毕以后,最终的输出值就是所输入的原始消息的SHA-256值.

图2 SHA-256算法流程
SHA-256通过将不定长的消息和文件等数据转换为固定长度为256b且难以区分的字符串来保护数据不被截取或篡改.相同的输入依据SHA-256计算的值是唯一的,但当输入有修改时,即使是很微小的修改得到的哈希结果也会完全不同.SHA-256算法的特点是易于检查,较难伪造,具有很强的抗强碰撞的能力.以现在的计算机破解需要消耗极大的资源,因此无法获得利益.但随着量子计算机的发展,SHA-256的安全性也将受到影响.据文献[19]显示,SHA-256的前量子安全级别为256b,预估后量子安全级别为128b.
其他传统经典哈希算法同样受到量子计算机不同程度的影响,具体如表2所示:

表2 传统经典哈希算法受量子计算机的影响情况
2.2 基于量子密钥的Toeplitz哈希算法
2018年,Kiktenko等人[27]使用Toeplitz哈希计算认证标签值,Toeplitz哈希计算简单,且在信息理论上是安全的.
Toeplitz哈希是一类特殊的通用哈希函数[28],基于Toeplitz矩阵进行哈希值的计算[29].维数为n×m的Toeplitz矩阵通过向量矩阵乘法可以将长度为m的原始消息计算为长度为n的哈希结果.Toeplitz矩阵是在左右对角线上具有常数值的矩阵.这种特定结构减少了构造随机矩阵时所需的随机比特数.例如,当构造m×n对角常数矩阵时,所需的随机比特数将从mn减少到m+n-1.
文献[27]采用的方案中,如果通信双方Alice和Bob共享一个其他人不知道的秘密私钥Kaut,则可以对接收到的对方消息进行身份验证.秘密私钥生成的前提是双方在会话开始时就有少量“种子”密钥来认证对方的身份.一旦建立了私钥,身份验证过程则是:Alice向Bob发送1条消息,其中包含使用该密钥生成的哈希标签.在收到消息后,Bob计算其哈希标记.如果哈希标记一致,Bob可以确定该消息是从Alice发送的.哈希标签的具体计算公式如下:
h(Mi)=TSMi⊕ri,
(1)
其中TS是由长度为lh+lM-1的字符串S生成的lh×lMToeplitz矩阵,ri是长度为lh的位串,⊕是按位异或,S和ri都是私有的,并且取自公共私钥Kaut.那么窃听者正确猜测已被修改消息的哈希标签的概率不超过2-lh.如果传输了一系列消息,则可以在不影响安全性的情况下再次使用字符串S,而每次都必须重新生成字符串ri.私钥以每条消息lh(单位为b)的速率被消耗.其中lh=40,lM=222.
如果一个装有量子计算机的恶意方离线伪造数据库.它将过去的一个交易记录更改为自己的利益,并对同一块中的其他交易的变体进行Grover搜索,以使其哈希保持不变,从而使伪造版本看起来合法.一旦搜索成功,它就会入侵所有或部分网络节点,并用伪造的版本替换合法数据库.然而,这种攻击造成重大损害的可能性似乎很低,因为攻击者需要同时攻击至少1/3的节点才能改变共识.此外,由于与经典搜索算法相比,Grover算法只提供了2次加速,因此可以通过将块哈希长度的约定增加到其安全非量子值的2倍来防止这种情况.
该哈希函数采用一次一密的加密方式,在信息理论上绝对安全[27],可以有效抵御量子攻击,为实现可扩展的量子安全区块链平台开辟了可能性.私钥生成前的“种子”密钥认证了通信双方的身份,为算法提供了更高的安全性,但是成本太高,无法大规模应用于实践.通信只在两方之间进行,第三方无法验证,存在通信一方作恶的可能性,窃听者也可以冒充2个授权用户(Alice和Bob)中的任何一个,以获得对机密数据和资源的未经授权的访问.
2.3 基于QIQW的量子哈希算法
2021年,Abd El-Latif等人[7]提出了使用基于QIQW(quantum-inspired quantum walks)的量子哈希函数链接区块链的块.量子漫步可以描述为希尔伯特空间元素到概率分布集合的非线性映射.这种性质加上量子漫步对初始条件变化的高度敏感性,使离散量子漫步可以被视为离散时间和离散值混沌系统.离散量子漫步的基本组成部分是硬币粒子、漫步空间、进化算子和1组可观察量.在这种情况下,如果量子漫步在有N个顶点的圆上运行,步行者是一个运行在基数为#(H)=N的希尔伯特空间H中的量子系统.受控交替量子漫步(controlled alternating quantum walks, CAQW)是由二进制串m控制的2维单步量子漫步.文献[7]中正是基于CAQW的混沌行为构建了量子哈希函数.
基于CAQW构建量子哈希函数(quantum hash functions, QHF)的步骤为:

2) 通过使用等式h=fix(Pi×108) mod 2g将概率矩阵P转换为比特串,获得二进制消息m的哈希值,其中哈希值的长度为N2×g(单位为b).
假设使用标准量子通信信道在发送方和接收方之间交换主密钥参数(N,α,β,θ0,θ1,θ2).交换的密钥参数在消息加密、解密和身份验证过程都是需要的.
Alice和Bob通过防篡改的量子安全信道交换初始参数(N,α,β,θ0,θ1,θ2).数字设备的计算精度为10-16,用于构造哈希值和密钥流的密钥空间允许为1096,这提供了额外的通信安全层.因此,基于QIQW的量子哈希函数可以防止消息攻击.
假设Bob收到交易信息后,Bob根据与Alice交换的初始密钥参数(N,α,β,θ0,θ1,θ2)从S提取哈希码hashA,从接收到的加密文本中提取哈希码hashB.接下来,将hashA与hashB一起比对.若发现加密文本并非Alice所发,该笔交易被丢弃.因此,基于QIQW的量子哈希函数可以防止无消息攻击.
当Eve冒充Alice并试图与Bob通信时,Eve无法访问初始参数(N,α,β,θ0,θ1,θ2)以操作QHF并向Bob发送未经授权的事务.Bob将通过身份验证过程检测到Eve的存在并丢弃此事务.同时,如果Eve冒充Bob并试图与Alice通信,Eve无法访问有关关键参数(调用QHF所需的参数)的信息违反交易数据的可能性.如前所述,QHF的巨大密钥空间使得违反事务数据变得不切实际.此外,如果Eve成功获得密码文本及其嵌入的哈希值(即Eve成功猜测了N),Eve无法获得受量子信道保护的完整密钥参数,就无法访问交易数据.因此,基于QIQW的量子哈希函数可以防止模拟攻击.
基于QIQW的量子哈希函数可以抵御来自数字和量子计算机的可能攻击[7],从而确保后量子时代物联网设备之间的数据安全传输.为基于量子启发模型设计区块链技术打开大门,是本文目前较为推荐的哈希方案.
2.4 基于Hilbert变换的量子哈希算法
2021年,Wen等人[30]提出了一种基于Hilbert变换的量子哈希算法,并与量子SWAP测试和量子隐形传态一起构造了一种具有后量子安全性的量子区块链系统.其中的量子哈希算法具体构造如下:
给定一个经典量子函数ψ,它将1个n位0/1字符串映射到1个具有n个量子位的量子态.
ψ:{0,1}n→(H2)⊗s,
(2)
其中
(H2)⊗s=H2⊗…⊗H2=H2s
(3)
是由s个量子位的单个量子位状态空间组成的2s维Hilbert空间中的单位向量.函数ψ也可以用狄拉克符号表示为ψ:ω→|ψ(ω)〉.
如果ψ满足以下2点则为量子单向函数:
1) 容易进行正向计算.即存在1个量子算法可以满足在多项式时间内计算任何输入ω的输出|ψ(ω)〉.
2) 根据给定的|ψ(ω)〉值无法计算出ω.即根据量子信息理论,无法从|ψ(ω)〉得到ω.
|ψ(ω)〉的性质:如果n≫s,那么就不可能从给定的|ψ(ω)〉中获得ω的值.
对于任意1对输入ω和ω′,ω≠ω′,如果函数ψ的映射是ω→|ψ(ω)〉,则|ψ(ω)〉和|ψ(ω′)〉是δ-正交,即|〈ψ(ω)〉|ψ(ω′)〉|<δ,该函数称为δ-resistance函数.
如果函数ψ:{0,1}n→(H2)⊗s同时是一个量子单向函数和δ-resistance函数,那么这个函数被称为(n,s,δ)量子哈希函数.
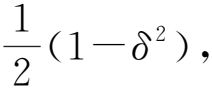
根据输入情况不同,将判定结果中测量结果、测量结果概率、判定结果、是否判定正确的统计如表3所示:

表3 不同输入情况的判定结果统计


2.5 基于数学困难问题的哈希算法
1900年,德国数学家Hilbert[31]在巴黎第2届国际数学家大会上作的题为《数学问题》的著名讲演中,提出23个问题作为对未来数学家的挑战,整系数多项式是否存在整数解的难题正是其中的第10个.1970年苏联数学家马蒂塞维奇最终证明:在一般情况下,答案是否定的.
求解整数多项式方程组的问题就是找到一个可行的办法,通过有限次的运算确定含有任意多个未知数的整系数不定方程fi=(x1,x2,…,xn)=0,i=1,2,…,m的解.该问题在算法上无法解决,此外,如果多项式的次数≥3且n>m,那么这个问题在算法上是整数不可解的.
2018年,Krendelev等人[32]提出了一种哈希函数构建方法,该方法基于求解整数多项式方程组的问题,并使用1组参数增强哈希函数持久性,其中方程的数量小于未知参数的数量.
该方法在构建时需要首先确认参数,在基础版本中,需要确认的参数有:模块p,维度大小m×n,开始系数集合α1,α2,…,αn,块的大小b,形成被加数h1(x),h2(x),…,hm(x)的规则.为了获得更好的结果,作者还制定了参数要求.所有计算都将在模块p上进行.模块应该是足够大的素数.根据从参数α1,α2,…,αn,αi∈导出的特殊规则生成一些向量集,其中n是任意整数,代表这些向量的维数为n.假设某个哈希文档由1组数字描述为x=(x1,x2,…),一定数量的比特组合形成1个数字,一定数量的数字组合形成1个条件块.块的位数可以是8,10,12等.该哈希算法的具体计算过程如下:
1) 数据准备.
根据输入文件准备1个十进制整数字符串x=(x1,x2,…,xm).
然后根据开始系数集合α1,α2,…,αn生成一个矩阵A=(a1,a2,…,am),其中ai根据公式ai=α1a1+α2a2+…+αnan构造为递归序列.
2) 构造哈希函数.
H(x)=[a1h1(x)+a2h2(x)+…+
amhm(x)] mod (p).
(4)
根据上述公式构建的向量即是哈希,其中函数h1(x),h1(x),…,hm(x)可以自己选择任何规则构建,也可以按照公式计算:
H(x)=[a1x1x2+a2x2x3+…+
amxmx1] mod (p),
(5)
哈希函数的输出字符串的大小为n×m.
3) 修改.
在大文件中,某些项为0的概率是很大的.其主要原因是当某些项的0累加时,形成一个递归序列的规则.为了在算法的基础版本中避免这种情况,作者使用循环移位的方法.或者直接将0分量替换为固定数,固定数也可以是一个参数.
该哈希算法对量子计算机具有抵抗力,并基于算法上无法解决的问题——寻找整数多项式方程组的解实现.所开发的算法是参数化的,因此哈希函数的结果取决于几个参数,只要参数有一点变化,函数的值就会发生很大变化(雪崩效应),大大增加了决策时间.按位比较,雪崩效应约为47%~50%,它能够抵抗冲突.碰撞在理论上是可能的.然而,为该哈希算法找到冲突是没有意义的,因为如果方程组中存在次数大于3的多项式,则问题在算法上是无法解决的,因此碰撞是不可能的[32].但是同基于概率分布矩阵的量子哈希函数,秘密参数的知悉范围非常关键,若范围太大则很容易遭受敌人攻击,范围太小则不易于第三方进行消息验证,秘密参数知悉范围的选取建议根据实际问题进行具体判定.
3 哈希函数设计建议
区块链对未来数据存储至关重要,而区块链中哈希函数的安全性更是时刻影响着区块链的总体安全性,因此研究具有抗量子性的哈希函数为区块链在后量子时代的稳健运行提供有力基础具有十分重要的意义.本文在以上提出的5种哈希方案中,目前最推荐2.2节中基于QIQW的量子哈希函数,可以抵御来自数字和量子计算机的可能攻击.2.3节中的方案由于存在误差,所以目前不推荐,未来消除误差后,将其应用到区块链中也是一个不错的选择.
除此以外,经过分析与总结,本文建议在未来区块链的设计中遵循以下3个原则:

3) 带有秘密参数的哈希函数.若存在量子攻击的可能性,推荐使用带有秘密参数的哈希函数.使用量子加密通信等可信信道来传输秘密参数,利用量子物理特性来保证秘密参数的机密性,从而抵御经典或量子计算机可能的攻击.
4 结 语
本文对哈希函数的量子计算攻击及其对区块链的影响进行了分析,对当前的5类抗量子攻击的区块链中的哈希函数进行了分析、对比和总结,最后对区块链中的哈希函数的设计给出了几点建议,本文的工作将为后量子时代区块链中的哈希函数的设计提供有益参考,下一步将针对量子时代的区块链的特性和不足,提出新的抗量子设计方案,在轻量化、抗碰撞性、安全性上等取得更好的发展.
