Stability of the Stratification of Water Bodies in the North Passage of the Yangtze River Estuary Based on the EFDC Model
2024-03-12WUDeanLIXinandWANGYigang
WU De’an , LI Xin , and WANG Yigang
1) College of Harbor, Coastal and Offshore Engineering, Hohai University, Nanjing 210098,China
2) Tianjin Research Institute For Water Transport Engineering, Tianjin 300456,China
Abstract To study the stratified stability of a water column in the North Passage of the Yangtze River Estuary, a numerical model of the hydrodynamics of this estuary is established using the EFDC model. On the basis of EFDC results, this paper derives and provides the discriminative index of water body stability caused by salinity and analyzes the along-range variation in water body stratification stability in the North Passage of the Yangtze River Estuary and the periodic variation at a key location (bend area) based on the simulation results of the numerical model. This work shows that the water body in the bend area varies between mixed and stratified types, and the vertical average flow velocity has a good negative correlation with the differential velocity between the surface and bottom layers of the water body. The model simulation results validate the formulae for the stratified stability discriminant during spring tides.
Key words Yangtze Estuary; North Passage; EFDC model; stratification stability; salinity distribution
1 Introduction
An estuarine area is the region of transition from river to ocean, and it is also the zone where multiple dynamic factors interact with each other. In an estuary with abundant water, the runoff has the extremely obvious effect of diluting seawater in the nearby marine area, while the strong tide transports high salinity brackish water into the estuary, and the interaction of high-density seawater and low-density freshwater causes the salinity to spread from the bottom to the upper reaches. Saltwater intrusion not only deteriorates water quality ecology but also directly affects the dynamic environment of the estuary area, such as the estuarine circulation, maximum turbidity zone, stagnation point, and sediment flocculation, and directly affects the sediment transport and geomorphological evolution of the estuary, such as entrance bar.
Estuarine stratification refers to the difference in water body density in the vertical direction, and stable stratification refers to when the density is greater in the bottom layer than in the surface layer. In estuarine areas affected by runoff and tidal currents, estuarine mixing and stratification transform each other, while the kinetic and potential energies of the water body transform each other. The phenomenon of water column stratification was first observed in the Tay Estuary by Fleming in the United Kingdom (Fleming, 1818), Dyer (1997) and Zhaoet al., (2019)suggested that although the density difference between salt and freshwater is only 2%, it is sufficient to cause density circulation, resulting in an upward movement of saltwater at the bottom layer and a flow of upper diluted water to the ocean, forming a saltwater wedge and generating internal wave fluctuation friction at the salt and freshwater interface. When the velocity difference between the upper and lower layers is further expanded, vertical turbulence destroys the interface, mixing saltwater and freshwater, and the estuary gradually transitions from stratified to partially mixed to fully mixed. The estuarine mixing type depends on the strength of the vertical structural stability of the flow,which can be described by the Richardson number (Richardson, 1920), which is the ratio of the buoyancy effect to the vertical turbulence effect. Generally, when the Richardson number is less than 0.25, the turbulence effect can destroy the density stratification and produce water mixing.
The observation results show that the variation in tide and runoff, as well as the influence of strong wind and waves, can cause the stability intensity of the vertical structure of the estuary water stratification to change with time. Simpson and Souza (1995) observed a decrease in the vertical mixing of the Rhine flushing water in the North Sea region with approximately 12-hour fluctuations and thus attributed it mainly to the interaction between tidal straining and the density gradients of the onshore currents.Subsequently, this phenomenon has been found successively in estuaries. By comparing Richardson numbers in a study of the boundary layer structure of the Hudson River Estuary, Nepf and Geyer (1996) found that although the height of the water column where mixing effects occur during flood and ebb tides is similar, tidal strain can cause very substantial mixing in the lower layer of the estuary during ebb tide, while during flood tide the mixing is restricted to the lower near-bottom layer. Staceyet al.(2001)analyzed acoustic Doppler current profiler residual flow data in North San Francisco Bay and concluded that this asymmetry during flood and ebb tide stratification can also lead to estuarine circulation. Geyeret al.(2000) used the measured velocity, density, and pressure gradient to calculate the contribution rates of the momentum equation and found that the calculated vertical turbulent viscosity had considerable tidal deformation, and its value during flood tide was twice that during ebb tide. This result showed that tidal deformation weakened the stability of the stratification of the estuarine water body during flood tide.
In addition to the change in the stability of water stratification during the tidal cycle, the inter-month variation,such as the spring-neap tide cycle and fortnightly variation in the magnitude of the tide, can also lead to changes in the stratification of the estuarine water column (Jay and Smith, 1990; Uncles and Stephens, 1996). Sharpleset al.(1994) calculated and analyzed the vertical structure of the water body in the York Estuary using 61-day measured data in the upper part of this estuary and the mathematical model closed by the Mellor-Yamada second-order turbulence model. They found that the vertical density structure has a similar periodic relationship with the mixed stratification change. Comparison with the tidal current velocity revealed that when the spring tide is strong, weak stratification or full mixing occurs, whereas when the corresponding neap tide velocity is weak, strong stratification can be developed and improved. Scully and Geyer (2012)studied the physical processes and tidal strain of stratification in the Hudson River Estuary and concluded that in some estuaries with strong runoff effects, the tidal strain during ebb tide can lead to enhanced water body stratification effects.
The Yangtze River is the largest river in China and combines strong runoff and tidal action to produce a high suspended sediment concentration and dynamically energetic estuary. In the main forks of the Yangtze River Estuary,differences are observed in the degree of estuarine stratification and the presence of estuarine circulation under the combined influence of salinity gradients and runoff currents (Shenet al., 1986). Liet al.(2013) studied the straininduced periodic stratification in estuaries and gaveRi= 1 as a judgment parameter for the stability of water bodies in the Yangtze River Estuary using the Richardson number (Richardson, 1920). Niet al.(2012) concluded that the surface water column of the Yangtze River Estuary plume is well mixed, and the bottom water column is weakly mixed, based on the measured data of the estuary. To study the estuarine salinity diffusion and stratification mixing mechanism under the dynamic process of the Yangtze River Estuary circulation, Li and Tong (2016) used a three-dimensional model of the estuary (Delft 3D-FLOW) to simulate the effect of the salinity stratification diffusion pattern and diffusion coefficient changes on estuarine stratification in this estuary, clearly showing through sensitivity analysis the effect of the turbulent diffusion coefficient on the diffusive transport, vertical stratification, and mixing of salinity.
2 Mathematical Model of EFDC
2.1 Governing Equation
The hydrodynamic governing equations of the EFDC model mainly apply to the turbulent water motion within a fully developed boundary layer with incompressible volume and variable density in wide shallow waters, and the hydrostatic assumption is used in the vertical direction.
To better fit the actual boundary, the EFDC model adopts orthogonal curve coordinates or the Cartesian coordinate system in the horizontal direction and aσcoordinate system in the vertical direction, expressed as follows:
In this formula, ‘*’ represents the original actual vertical coordinates, and −handζare the actual vertical bed topography and free surface fluctuations, respectively.
After transforming the equation of motion of turbulent water flow in the boundary layer under the assumption of hydrostatic pressure and adopting the Boussinesq approximation, the momentum equation, continuity equation, and transport equations for salinity and temperature can be derived in the following form.
Momentum equation:
Continuity equation:
Eq. (5) integrated over the interval of [0, 1] with the boundary conditionsw= 0 atz= (0, 1) yields the continuity equation averaged along the water depth:
Transport equations for salinity and temperature:
The velocitywin theZdirection after coordinate transformation and the vertical velocityw*before coordinate transformation are related as follows:
In these equations,uandvare the horizontal velocity components in thexandydirections in the orthogonal curvilinear coordinate system, respectively.mx, myis the horizontal coordinate transformation factor (Lamé factor),m=mxmy.His the instantaneous total water depth,H=h+ζ.ζis the instantaneous water level.his the distance from the mean sea level to the sea floor.pis the part of the actual pressure that exceeds the static pressureρ0gH(1−z)of the reference density divided by the reference density.ρ0is the reference density;fis the Coriolis force parameter.Avis the coefficient of viscosity of the vertical turbulence.Qu, Qvis the source-sink term of the momentum equation (horizontal momentum diffusion at subgrid scale);andAbis the vertical turbulence diffusion coefficient.
The continuity equation uses the hysteresis approximation, in which the water densityρis related to the water temperatureTand salinityS, and the water pressure also have a weak impact on it (Clark and Hall, 1991; Mellor,1991). In Eq. (4),bis the buoyancy term; similar to the momentum equation, the transport equations for salinity and temperature, Eqs. (8) and (9), respectively, contain the source and sink itemsQsandQT. This includes subgrid-scale horizontal turbulent diffusion and the source and sink effects of heat.
2.2 Boundary Conditions
2.2.1 Vertical boundary conditions
At the upper surface:
At the lower surface:
In the above formula,τbx, τbyis the shear stress atσ= 0.τsx, τsyis the shear stress atσ= 1.Uw, Vwis the wind speed at 10 m above the water surface.ubl, vblis the bottom flow rate. The bottom drag force factorcbis
in which,κis the Karman constant, generally 0.4, ∆1is the dimensionless thickness of the bottom layer, andz0=z0*/His the dimensionless rough length. The drag coefficient of wind stresscsis:
In this equation,ρais the atmospheric density, andρwis the water density.
In turbulent models, the calculation of turbulent energy and mixing length also requires the corresponding vertical boundary conditions:
In Eqs. (15) – (17), the absolute value indicates the magnitude of the contained vector.
2.2.2 Lateral boundary conditions
The lateral boundary conditions mainly include open and closed boundary conditions. The open boundary condition is the driving force from outside the computational domain.The EFDC model can set the tidal level process, velocity process, and discharge process as hydrodynamic open boundary conditions. For the hydrodynamic simulation of estuaries, the tidal level and discharge processes are generally used as the open boundary condition. The closed boundary condition generally describes the situation of the water-land interface. The ‘solid wall’ condition is adopted;that is, the velocity component perpendicular to the boundary is zero.
2.3 Modeling the Yangtze River Estuary and Validating the Model
2.3.1 Modeling the Yangtze River Estuary
The Yangtze River Estuary is a delta-type estuary. The reach of the Yangtze River from the tidal boundary near the Datong Hydrological Station to the tidal boundary near the Jiangyin Hydrological Station is called the near-estuary section of the Yangtze River Estuary and is dominated by runoff. The reach from the tidal current boundary adjacent to Jiangyin to the entrance at the top of the Yangtze River Estuary bar is called the estuary section, which is affected by runoff and tidal currents. The water region from the estuary entrance of the Yangtze River eastward to the water region with a depth of 30 – 50 m in the open sea is called the coastal section outside the estuary of the Yangtze River and is mainly affected by tidal currents. During the dry season, the salt-water boundary of the Yangtze River Estuary is near Wuhaogou in the south channel and near Liuyao Port in the north channel.
The model simulation region includes the entire Yangtze River Estuary area and Hangzhou Bay as well as the adjacent marine area: The upstream boundary is located at the estuarine section of the Jiangyin Hydrological Station,the northern boundary of the outer sea is approximately 32.5˚N north of Lushi Port, the southern boundary is approximately 29.25˚N south of Zhoushan Island, and the eastern boundary is approximately 50 m isobath of the outer sea at 124.5˚E. The area of the model is approximately 104400 km2, as shown in Fig.1, and the calculation grid of the model is 216 × 162, as shown in Fig.2.
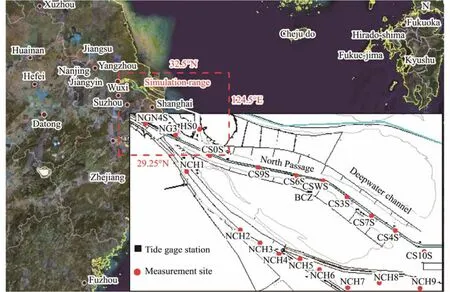
Fig.1 Range of models and the distribution of some hydrological stations.
Fig.2 Model grid diagram.
The grid is densely distributed in the estuarine section,which can potentially reflect the hydrodynamic variation in the Yangtze River estuarine water more accurately. The simulation water domain is verticallyσstratified, with 12σstratified layers of equal depth dissected from the surface to the bottom. The detailed setup and validation of the model are shown in the literature (Li, 2012). It is shown that the established 3D hydrodynamic numerical model of the Yangtze Estuary can be used to study the hydrodynamic characteristics of the Yangtze Estuary waters.
The definite solution conditions of the model include initial conditions and boundary conditions, and together with the control equation, they form a definite solution problem that can be solved.
The initial conditions of the model are a cold start; that is, the tide level and flow rate are zero. For the open-sea boundary conditions, the hourly hydrograph of the water levelζ(t) is given as follows:
which is provided by the calculation results of the East China Sea model.
The upstream boundary of the model is taken from the Datong section, and the boundary condition is the measured daily average flow at the corresponding time of the Datong Station. Considering that the runoff of the Qiantang River accounts for a small proportion, the flow of the Qiantang River is set as 0 in this paper.
Considering the simulation scope of this model, this study uses the salinity field obtained after three months of continuous simulation calculation with a value of 0 as the initial salinity condition. The salinity of the upstream boundary of the model is taken as 0. According to the statistical data observed throughout the year outside the Yangtze River Estuary, the salinity value of the model is 15 – 30 along the southern boundary from land to open sea, 30 – 35 along the eastern boundary from the southern open sea boundary to the northern open sea boundary, and 30 – 35 from land to open sea along the northern open boundary.
2.3.2 Model simulation accuracy evaluation
To better evaluate the simulation accuracy of the model,this paper uses the Nash-Sutcliffe efficiency indexEns(Tanet al., 2021) with high recognition to reflect the matching degree between the model simulation value and the measured value. The calculation results are as follows:
Here,Yobsis the measured value,Ysimis the simulation value, andnis the actual measurement times. The closer the value ofEnsis to 1, the better the fitting between the simulation value and the actual measured value. Referring to the previous evaluation system for numerical model simulation results (Moiasi, 2007), Nash-Sutcliffe efficiency is divided into four grades, as shown in Table 1.

Table 1 Evaluation grade classification of simulation results
The measured data of flow velocity and salinity during spring tide at the test points CS0S, CSWS, and CS4S in the North Passage of the Yangtze River Estuary and NCH1,NCH3, and NCH7 in the South Passage, as shown in Fig.1,are selected for a better evaluation of the simulation accuracy of the model. The evaluation results are shown in Table 2 and Table 3.

Table 2 Evaluation of velocity simulation accuracy during spring tide
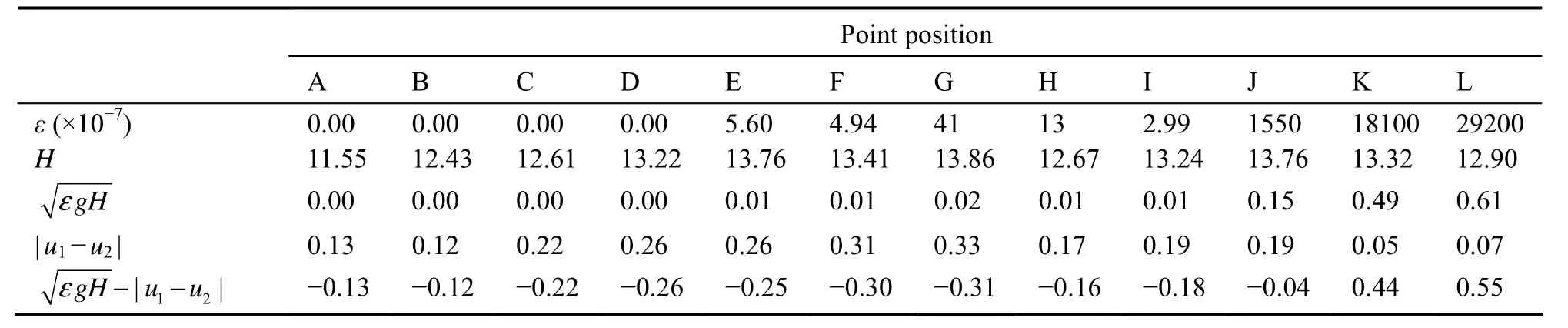
Table 4 Variation in water stratification along the North Passage during spring tide in the flood season
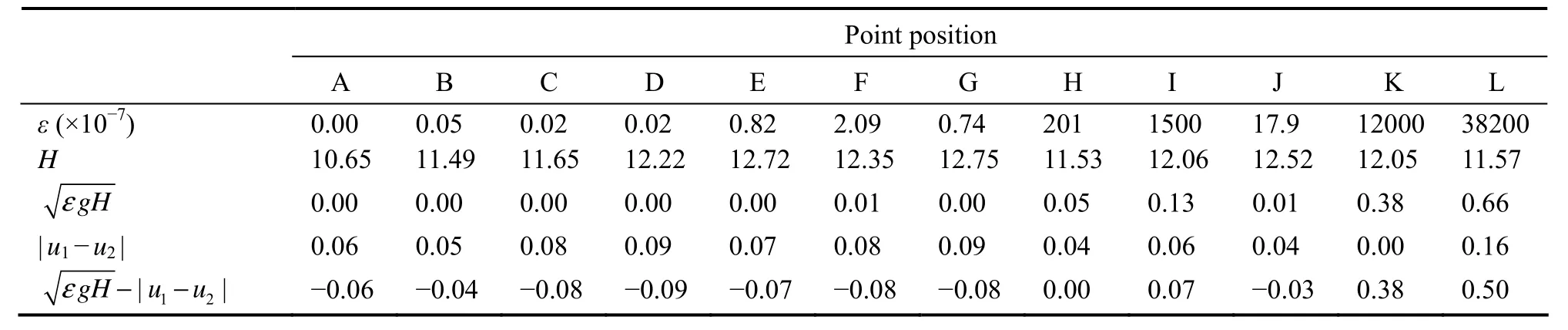
Table 5 Variation in water stratification along the North Passage during neap tide in the flood season

Table 6 Variation in water stratification along the North Passage during spring tide in the dry season
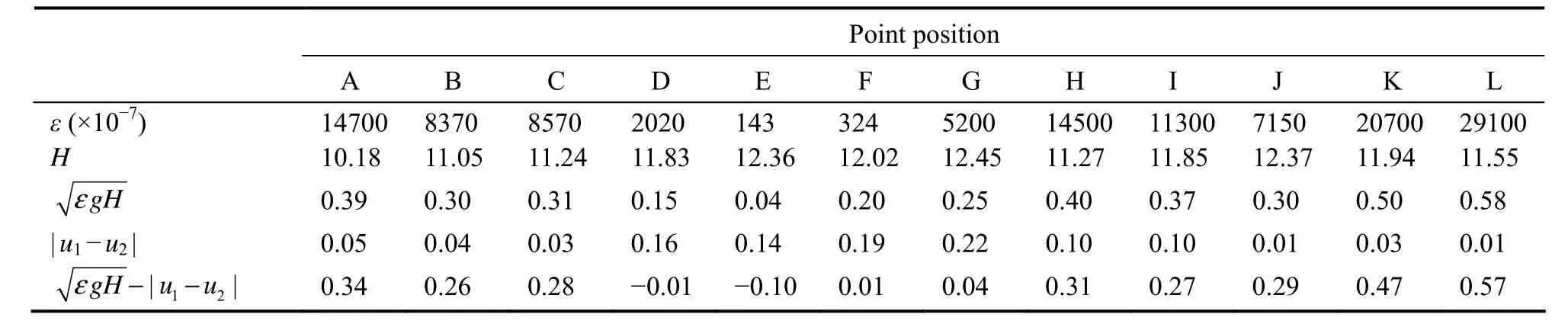
Table 7 Variation in water stratification along the North Passage during neap tide in the dry season
Table 2 and Table 3 show that the flow velocity and salinity Nash efficiency coefficient of each selected test point during spring tide are at or above the second level.Because of the limitation of paper length, the accuracy evaluation results of the model during neap tide are omitted from this paper. The above results show that the model can accurately simulate the temporal and spatial changes in the hydrodynamic and salinity fields of different tidal patterns in the Yangtze River Estuary and adjacent marine areas and can be used for relevant research.
3 Stability of Water Stratification
3.1 Stability Index of Water Stratification
The stratification characteristics of the Yangtze estuarine waters are important for the estuarine water and sediment transport and environmental changes, and the stability of stratification is closely related to the turbulent mixing intensity. Jin and Zhang (1992) obtained the critical conditions for the stability of warm and cold water stratification based on the experimental results.
whereV2/V1is the upper and lower water flow velocity ratio, andF0is the density Froude number. WhenF0>(F0)cr, which is unstable stratification after the confluence of warm and cold water, Eq. (19) is also suitable for salt and freshwater confluence flow situations. This suitability emerges because the spatial and temporal changes in water layer temperature and salinity ultimately lead to the distribution changes in water body density, and the process of water body stratification and mixing is actually the spatial distribution form and change process of water body density.
According to Sloff (1997), the characteristic line method for deriving the stratified water flow in reservoirs can be derived from the one-dimensional density stratified flow characteristic equation, and using theoretical analysis, the critical condition for the stratified stability of salt and freshwater mixing is derived (Li, 2012). The equation is simplified according to the various magnitudes of the equation to obtain the internal flow velocity of the density flow internal wave and the external flow velocity of the disturbed microamplitude wave. Here, the internal flow velocity is:
The internal characteristic flow velocity (20) illustrates the internal wave effect of the density flow. When the difference between the upper and lower density layers of the stratified flow (ε) is larger, and the difference in flow rate(|u1−u2|) is smaller, then the internal wave propagation velocity of the density flow will be larger.
Notably, whenεis smaller and |u1−u2| is larger, the internal wave velocity of the density flow tends to 0, and the density stratification tends to be unstable. From Eq.(20), we obtain the following:
In this equation,h1andu1are the thickness and flow velocity of the upper water body, respectively; andh2andu2are the thickness and flow velocity of the lower water layer, respectively.gis the acceleration of gravity.ρ1andρ2are the densities of the upper and lower layers, respectively, as shown in Fig.3. The coefficientεis expressed as Eq. (22).

Fig.3 Density of stratified flow (two layers).
Neglecting the effect of temperature change on density,the relationship between density and salinity can be approximated as follows:
Substituting Eq. (23) into Eq. (22), we obtain:
In this equation,α= 7.7 × 10−4psu−1. Substituting Eq. (24)into Eq. (21), the critical index of stratification stability for salt and freshwater mixing is obtained as follows:
In this equation,H=h1+h2. Eq. (25) shows that the salinity stratification is mainly related to the difference in flow velocity and salinity between the upper and lower streams. The equation obtained in this paper has the same magnitude and a similar basic structure as Eq. (19).
3.2 Distribution of Water Stratification and Mixing Along the North Passage of the Yangtze Estuary
3.2.1 Numerical simulation results and analysis
Fig.4 schematizes the along-range measurement point locations. On the basis of the results of the numerical model,Eq. (25) is used to calculate and explore the along-range variation characteristics of water stratification in the North Passage. Fig.5 shows the vertical distribution of salinity along the North Passage at different periods obtained from the simulations. This figure shows that the North Passage has different forms of saltwater intrusion and different types of salt and fresh water mixing along the Deep Water Channel under different runoff and tide effects. During the flood season, the 2 × 10−6isosalinity line oscillates between measurement points J and K. The outlet section of the North Passage is basically weakly mixed and partially mixed,while the inlet section and the bend area are strongly mixed.During the dry season, saltwater intrusion is more severe.From the spring tide in the dry season, the 2 × 10−6isopleth line invades the upstream, and it enters the South Channel from the North Passage upstream at the neap tide in the dry season. During this period, the stratification along the North Passage is more complicated: At the spring tide during the dry season, the lower part of the bend area to the outlet section is weakly mixed and partially mixed, and the upper part of the bend area to the entrance section is strongly mixed. The water stratification in the North Passage varies from weakly mixed to partially mixed and then to weakly mixed from the outlet section to the upstream section under the combined effect of runoff and tide.
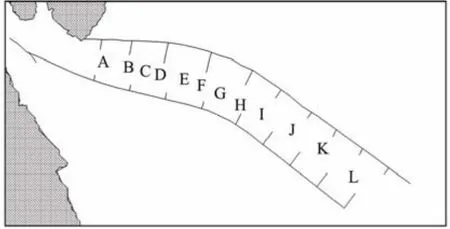
Fig.4 Schematic of the locations of the measurement points along the North Passage.

Fig.5 Typical distribution of salinity along the North Passage (a) during spring tide in the flood season; (b) during neap tide in the flood season; (c) during spring tide in the dry season; (d) during neap tide in the dry season.
Define the differential current velocity as:
WhenDu> 0, the water flow can maintain stratified flow,and conversely, turbulent mixing is enhanced, and the water gradually becomes a mixed flow.
According to Eqs. (21) – (25), the variation characteristics of stratification and mixing of water bodies in the North Passage are calculated at four typical times: spring tide in the flood season, neap tide in the flood season, spring tide in the dry season, and neap tide in the dry season. The results are shown in Tables 4 – 7. Comparing the results in Fig.5 and Tables 4 – 7 shows that the stratification stability discriminant (25) is simple in structure and practical,consistent with the salinity profile distribution results.
During the flood tide, the differential velocities of points K and L are greater than 0 m s−1, indicating that the salinity stratification in the inlet section of the North Passage is more stable, while the differential velocities of point J are less than 0 m s−1but small, so the stratification stability is poor. At neap tide in flood season, the salinity stratification of points K and L is better, while the differential velocities of points H and I are greater than 0 m s−1but small, so the stratification stability remains poor. During spring tide in the dry season, the differential velocities of points I and L are greater than 0 m s−1. The stratification of the entire water body in the North Passage is good except for the differential velocity of points D and E, which is less than 0 m s−1and is a mixed flow.
The above conclusions indicate that the outlet section of the North Passage is basically a weakly mixed stratified estuary that is heavily influenced by the density oflongitudinal circulation. The bend area is less saline and better mixed during the flood season but may become a stratified estuary during the dry season because of the influence of saltwater intrusion when the density longitudinal circulation changes the flow velocity distribution in the bend area and increases the trapping effect of suspended sediment.
3.2.2 Validation of the above salinity simulation results
Entrusted by the Yangtze Estuary Waterway Administration of the Ministry of Transport, hydrologic and sediment measurements are annually arranged by the Changjiang Estuary Hydrologic and Water Resources Survey Bureau in flood and dry seasons to timely and accurately grasp the hydrological and sediment dynamics of the Yangtze Estuary area, analyze the impact of the surrounding wading projects on the hydrological and sediment changes in each branch of the Yangtze Estuary, and provide necessary basic data on water flow and sediment for the dynamic management of the maintenance and implementation of the deep water channel in the Yangtze Estuary as well as an analysis of the causes of the siltation of the deep water channel and a study of siltation reduction measures. The hydrologic test of the 2019 dry season was performed from January 21 to 30 for the two representative tides of spring and neap tides. From July 27, 2019, to August 3, 2019, a flood season full tide hydrologic test was conducted for the waters in the south channel, the North Passage, and the South Passage, and a spring tide hydrologic test was conducted for the north channel area from August 2, 2019, to August 3, 2019. On the basis of the above salinity measurement data of 10 vertical lines along the North Passage,as shown in Fig.1, SURFER software is used to plot the salinity profile along the North Passage on hour measurement time. According to the temporal and spatial variation in salinity distribution in the North Passage, the process of water mixing and stratification can be studied and analyzed. Fig.6 shows the measured salinity profile along the North Passage corresponding to the simulation results in Fig.5 above.
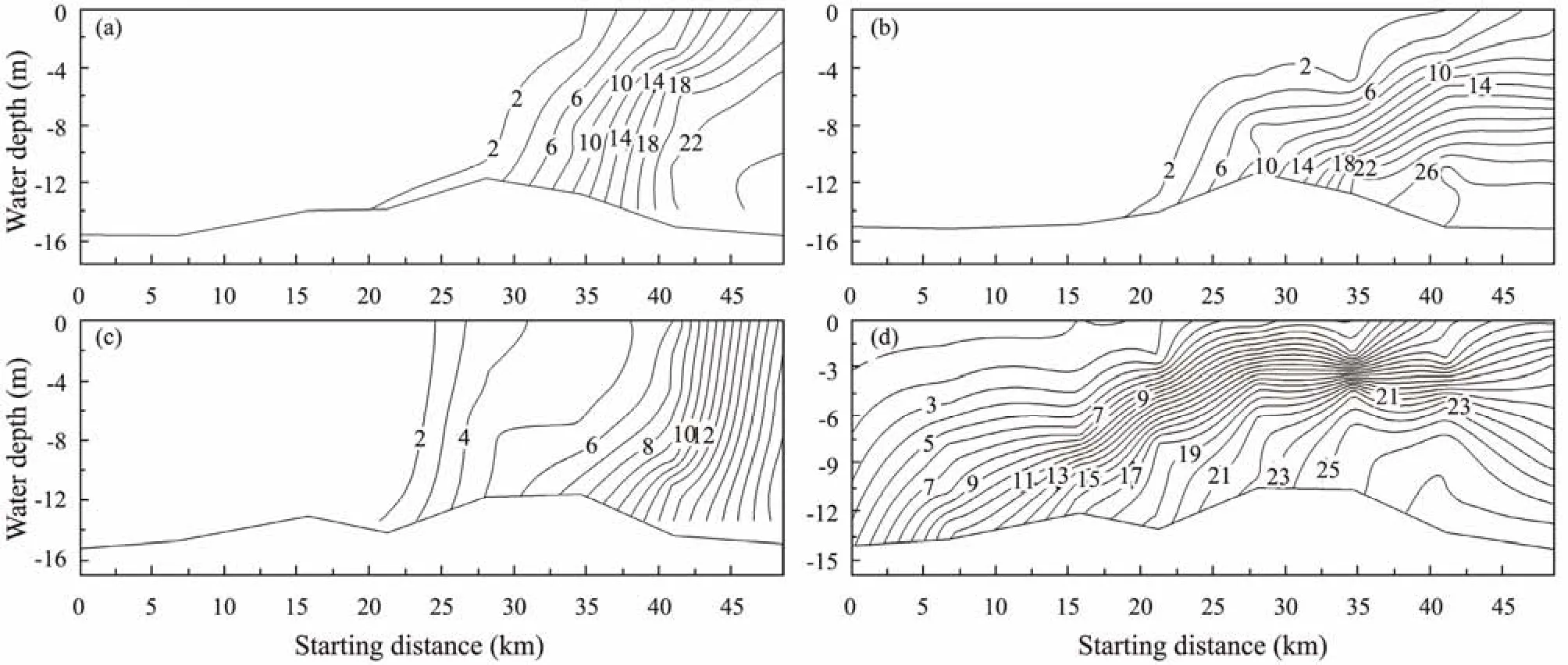
Fig.6 Observed salinity distribution along the North Passage, (a) at 2 h after the beginning of the flood during spring tide in the flood season (2019-08-03 10:00, the discharge is 52000 m3 s−1 at the Datong Station, and the tidal level is 0.44 m at the BCZ Tide Gage Station); (b) at 1 h after the beginning of the flood during neap tide in the flood season (2019-07-28 05:00,the discharge is 57300 m3 s−1 at the Datong Station, and the tidal level is 0.50 m at the BCZ Tide Gage Station); (c) at 1 h after the beginning of the flood during spring tide in the dry season (2019-01-21 06:00, the discharge is 23100 m3 s−1 at the Datong Station, and the tidal level is −1.36 m at the BCZ Tide Gage Station); (d) at 2 h after the beginning of ebb tide during neap tide in the dry season (2019-01-22 02:00, the discharge is 22700 m3 s−1 at the Datong Station, and the tidal level is 0.68 m at the BCZ Tide Gage station).
The numerical simulation results agree well with the measured stratified-destratified conditions, indicating that these results can be used as a tool to effectively study the stratification process of the Yangtze River Estuary. Importantly, since the terrain used in the model is not the terrain measured in 2019, the change in the terrain in the North Passage may explain the slight difference between the numerical simulation salinity profile and the measured salinity profile. The influence of topographic changes on salinity profile merits further study. In addition, a study (Zuet al., 2014) found that wind also plays an important role in the estuarine circulation structure and its related water stratification and mixing process. On the basis of the measured data, the establishment of a three-dimensional numerical model coupled with river flow, wind, tide, and salinity can further explore the response of the flow structure to wind and tide forcing (Zu and Gan, 2015).
3.3 Periodic Variation in Water Stratification in the Middle Part of the North Passage
To further explore the stratification of the water body in the bend area in the Deep Water Channel, the differential velocity of a typical tidal cycle process during spring tide in the dry season at measurement point G was calculated, and the results are shown in Table 8. The differential velocity process shows that the bend area is mainly a strongly mixed or partially mixed type, and the water stratification phenomenon only occurs in the short term.Additionally, the stratification stability of the water body in the bend area has more regular fluctuations with the tidal cycle, indicating that the stability of the water body is made more obvious by the tidal action. Therefore, the stratification stability of estuarine waters has not only longperiod changes in flood and dry seasons but also shortperiod changes in tides, which further indicate that the longitudinal circulation of estuarine density has similar periodic changes. In the case of a more stable upstream runoff, if the water column stratification is more stable, the strength of salinity density circulation is greater, and the interaction with tidal action may have an important influence on the sediment initiation, settlement, and transport process in the estuary area. Additionally, the turbulent diffusion effect of the water column may be inhibited when the water column is stratified (Geyer, 1993), causing much sediment to accumulate at the top of the landward side of the saltwater wedge and increasing the amount of back-silting there.
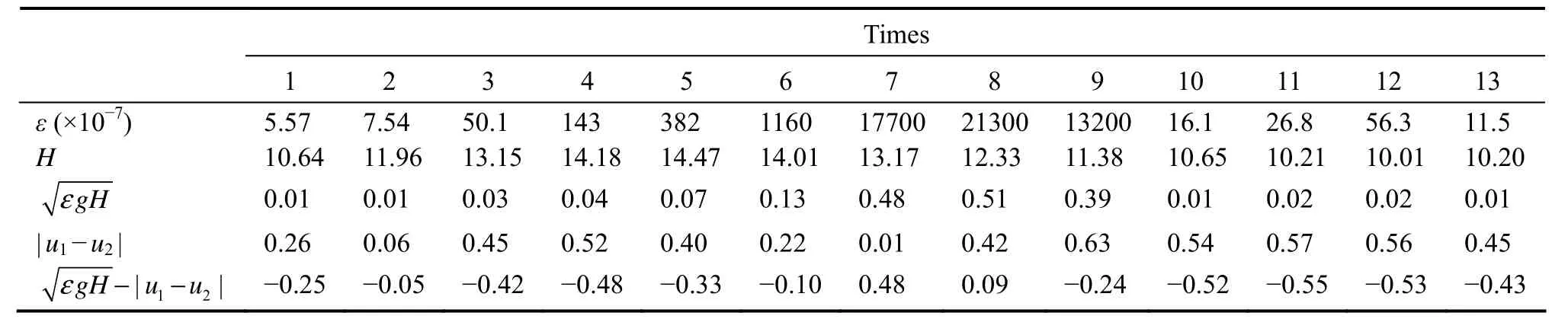
Table 8 Periodic variation in water stratification at point G in the middle part of the North Passage
The stability of water stratification is related to salinity distribution and tidal velocity. For a certain water area,the rate of change in salinity distribution is much lower than the rate of change in current velocity, so the relationship between vertical mean current velocity and differential velocity can be compared. Fig.7 shows the tidal cycle process curves of the vertical mean flow velocity and differential velocity of the water body at measurement point G.The results show a good negative correlation between the two, an increase in differential velocity with decreasing vertical mean flow velocity, and an enhancement of the stratification stability of the water body. As shown in Fig.7,when the vertical mean flow velocity reaches a minimum of 0.04 m s−1, the maximum differential velocity is 0.48 m s−1,and the estuary is a weakly mixed, highly stratified type.When the vertical mean flow velocity reaches a maximum of 1.6 m s−1, the minimum differential velocity is −0.55 m s−1, and the estuary is a strongly mixed type. When the vertical mean flow velocity is 0.6 m s−1, the differential velocity varies between ±0.1 m s−1, and the stratification of the water body becomes more unstable. Notably, in other periods, the bend area in the North Passage is affected by saltwater intrusion to a different extent, so the quantitative relationship between the vertical mean flow velocity and the differential velocity may differ, but they basically satisfy the negative correlation. Thus, for the bend area in the North Passage, the lower the current velocity is, the stronger the salinity density flow effect, and the effect of the saline wedge on sediment capture may also be enhanced.Thus, if the barotropic model is used to calculate sediment transport in the Yangtze River Estuary, the result of siltation may be smaller.
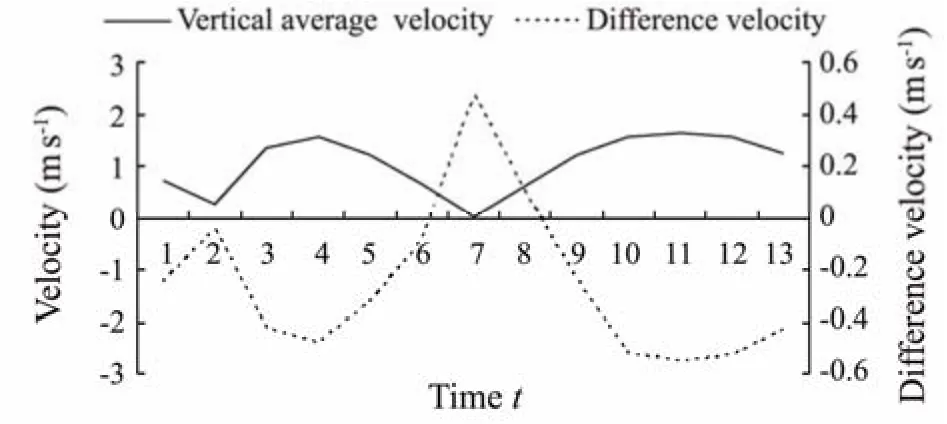
Fig.7 Periodic variation in average velocity and differential velocity.
4 Conclusions
In this paper, the three-dimensional coupled current- salinity model of the Yangtze Estuary established by the EFDC model is used to investigate the stratification characteristics of the waters in the North Passage, and the following main conclusions are obtained.
The differentiation index of water body stability due to salinity change is derived, and the along-range variation in water body stratification stability in the North Passage of the Yangtze River Estuary and the periodic variation in a key location such as the bend zone are analyzed based on the results of the numerical model. This analysis shows that the outlet section of the North Passage is basically a weakly mixed stratified estuary heavily influenced by the density-induced longitudinal circulation. The bend area is fresher and better mixed during the flood season but may transform into a stratified estuary during the dry season under the influence of saltwater intrusion when the density-induced longitudinal circulation changes the flow velocity distribution in the bend area and increases the trapping effect on the suspended sediment. The entrance section of the North Passage is similar to the bend area and may also form stratified flow when the saltwater intrusion is strong, affecting the suspended sediment transport and increasing the back-silting at this location.
The mixing type of the bend zone and the inlet section changes with time and space and the relative intensity of runoff and tidal action. The stratification stability of water movement in the bend zone in the middle part of the north passage correlates negatively with the vertical mean flow velocity when the salinity distribution does not change considerably, which proves the validity of the discriminant formula for stratified flow stability. During the spring tide in the dry season, the stratification of the water body in the bend area gradually shifts between mixed and stratified types with the change in the difference between surface and bottom flow velocities.
Acknowledgements
This research is supported by the National Natural Science Foundation of China ( Nos. 42176166, 41776024). The author of this paper is deeply grateful to Prof. Yixin Yan of the College of Harbor, Coastal and Offshore Engineering, Hohai University, for his pertinent suggestions in the writing and revision of this paper.
杂志排行
Journal of Ocean University of China的其它文章
- Using Natural Radionuclides to Trace Sources of Suspended Particles in the Lower Reaches of the Yellow River
- Eutrophication of Jiangsu Coastal Water and Its Role in the Formation of Green Tide
- Evaluation of the Shallow Gas Hydrate Production Based on the Radial Drilling-Heat Injection-Back Fill Method
- Microstructure Characterization of Bubbles in Gassy Soil Based on the Fractal Theory
- Morphological and Sulfur-Isotopic Characteristics of Pyrites in the Deep Sediments from Xisha Trough, South China Sea
- Deformation Characteristics of Hydrate-Bearing Sediments
