岩石物理驱动的储层物性参数非线性地震反演方法
2024-03-11潘新朋刘志顺高大维王璞郭振威柳建新
潘新朋, 刘志顺, 高大维*, 王璞, 郭振威, 柳建新
1 中南大学地球科学与信息物理学院, 长沙 410083
2 有色资源与地质灾害探查湖南省重点实验室, 长沙 410083
3 有色金属成矿预测与地质环境监测教育部重点实验室, 长沙 410083
0 引言
预测地层中的储层和进行有效的储层评价是地震勘探中不可或缺的关键步骤.储层物性参数可以影响弹性参数如纵、横波速度和密度,继而影响宏观地震响应如地震观测数据(Chiappa and Mazzotti, 2009; Zhao et al., 2014; Luo et al., 2019; 李坤等, 2020).叠前地震反演可以获取弹性参数,进而用于寻找和确定储层,然而反演得到的弹性参数无法有效的进行储层评价(Lu et al., 2018).储层物性参数如孔隙度、泥质含量和流体饱和度等在储层预测和流体识别方面具有重要作用,储层物性参数的获取可以为储层评价提供有力支撑(蒋炼等, 2011; 张佳佳等, 2020; 韩宏伟等, 2021; Grana et al., 2022;陈国飞等,2023).
通过地震数据可以估测储层物性参数,其中叠前地震反演和岩石物理反演发挥了重要作用.储层物性参数反演可以分为间接反演法和直接反演法两种,目的都是建立地震数据与储层物性参数之间的联系(Bosch et al., 2010).直接反演法是利用岩石物理模型将储层物性参数代入反射系数方程,岩石物理模型通常是非线性的,这个过程往往会将岩石物理模型简化,并且新的反射系数方程一般会将孔隙度或流体饱和度参数化形成一个孔隙项或流体项(Aleardi et al., 2017; Pan et al., 2017; 潘新朋等, 2018b; Pan and Zhang, 2019a,b).间接反演法主要分为两步,首先通过地震反演从地震数据中获取弹性参数,其次利用弹性参数估测储层物性参数(巴晶等, 2013; Grana, 2016; Ba et al., 2017).对于弹性参数反演问题,传统的确定性反演方法可以得到一组最佳拟合的模型参数,但是不能体现反演结果的不确定性(Tarantola, 2005; Huang et al., 2020; Grana et al., 2022).叠前AVO(振幅随偏移距变化)反演问题具有不适定性,并且地震数据受到噪声、频带限制等因素的影响,因此除了获得稳定的反演结果外,有必要表征反演结果的不确定性(Wang et al., 2022; Junhwan et al., 2022).利用贝叶斯反演方法可以有效实现弹性参数的反演,并对反演结果的不确定性进行分析(Buland and Omre, 2003; 潘新朋和张广智, 2019; Li et al., 2022).通过简化岩石物理模型的直接反演法会降低模型的精确性并引入误差,并且可能无法获取直观的物性参数(Pan and Zhang, 2018).物性参数间接反演法应用比较广泛,将反演得到的弹性参数和物性参数相结合可以更有效的进行储层表征.
储层物性参数的反演依赖于岩石物理模型,岩石物理模型是建立储层物性参数与弹性参数之间联系的纽带.构建的岩石物理模型主要有三种,分别是经验岩石物理模型、统计岩石物理模型和理论岩石物理模型.有些经验岩石物理模型直接将纵波速度、横波速度等效为孔隙度的函数(Dvorkin, 2008).统计岩石物理模型是通过测井数据建立物性参数与弹性参数或弹性阻抗之间的统计关系,进而估测物性参数(Bachrach, 2006; Grana and Della Rossa, 2010; 印兴耀等, 2014;张冰等, 2018).经验岩石物理模型并不精确,统计岩石物理模型一般只在特定探区内适用,而基于岩石物理理论构建的岩石物理模型精确性更高、适用性更广.理论岩石物理模型的构建主要分为两步,第一步先由岩石基质的模量推导出岩石骨架的模量(Kuster and Toksöz, 1974; Nur, 1992; Xu and White, 1995; Guo et al., 2021).第二步由孔隙流体出发,通过各向同性或各向异性的Gassmann方程由岩石骨架的模量推导出饱和岩石的模量,再通过饱和岩石的模量将弹性参数表示为物性参数的函数(Gassmann,1951; 陈怀震等, 2014; Guo et al., 2021).
岩石物理模型通常是非线性的,因此为了便于反演可将复杂的岩石物理模型做泰勒展开,进而得到其一阶乃至高阶的近似表达式,然而这或许会降低岩石物理模型的精确性并增加岩石物理反演的误差,并且该方法不适用于高度非线性的岩石物理模型.Grana(2016)将岩石物理模型线性化并保留泰勒一阶近似表达式,采用线性贝叶斯反演方法实现物性参数的估测.Lang和Grana(2018)在Gray近似式的基础上,将岩石物理模型线性化后基于Jacobian矩阵利用地震数据反演得到模量、密度和孔隙度.当岩石物理模型较为复杂或初始模型较差时可以选取非线性反演方法.非线性反演方法对初始模型要求较低,并且可以在全局范围内寻找最优解.马尔可夫链蒙特卡罗(MCMC)是对随机变量的概率分布进行抽样的统计算法,可应用于地球物理反演问题(潘新朋等, 2018a; Zhang et al., 2021;赵容容等,2022).Zunino等(2015)在贝叶斯框架下,利用MCMC算法从地震数据中估测目标储层带的岩石相和孔隙度.李红兵等(2021)基于Gassmann方程从弹性阻抗出发利用模拟退火算法实现了孔隙度、含水饱和度和等效孔隙扁度的反演.Guo等(2021)采用模拟退火算法对目标函数进行优化,实现了储层物性参数的估测.刘财等(2017)将粒子群算法应用于页岩孔隙纵横比反演,并以反演得到的孔隙纵横比为约束实现横波速度的预测.粒子群优化算法(PSO)是一种有效的全局优化算法,其原理简单、参数设置少并且易于实现,可有效用于储层物性参数的估测.
在储层物性表征问题中,复杂的岩石物理模型具有非线性特征,岩石物理模型线性化反演方法有一定局限性(Grana, 2016; 张佳佳等, 2020; Guo et al., 2022).经验岩石物理模型有时与实际地质情况偏差大,通过测井数据得到的统计岩石物理模型可能无法在多个探区内同时适用.因此,本文以碎屑岩储层为例,提出了岩石物理驱动的储层物性参数非线性地震反演方法.首先基于贝叶斯框架和高斯分布约束条件,利用线性贝叶斯AVO反演方法从叠前地震数据中实现纵、横波速度和密度等弹性参数的估测.然后选取Gassmann方程和临界孔隙度模型针对碎屑岩进行岩石物理建模,通过非线性岩石物理模型建立起弹性参数与物性参数之间的联系.最终利用粒子群算法进行全局寻优获得较为准确的物性参数.合成数据和实际资料的测试结果验证了所提方法的可行性和准确性,反演得到的弹性参数和物性参数可有效用于储层预测和表征.
1 理论和方法
1.1 地震正演模型
地震振幅可以等效为纵波反射系数与地震子波相褶积的值.精确的纵波反射系数公式较为复杂,通常采用Zoeppritz方程的近似式来简化计算,其中Aki-Richards公式形式简单、应用方便(Aki and Richards, 1980).具体表达式为
(1)
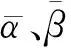
(2)

RPP=ADm,
(3)
其中:
(4a)
并且:
m=[lnα,lnβ,lnρ]T,
(4b)
其中A是与入射角有关的系数矩阵;m表示模型参数,其为弹性参数的对数形式;D是微分矩阵,对模型参数m起到求导的作用.
假设模型参数m的先验分布服从先验均值为μm、先验协方差矩阵为Cm的高斯分布.叠前地震振幅d表示为子波矩阵W、系数矩阵A、微分矩阵D和模型参数m的乘积再加上噪声项e,d表达式如下:
d=WADm+e,
(5)
其中:
m~Nnm(μm,Cm),
(6)
式中,假设噪声项e服从均值为0,协方差矩阵为Cd的高斯分布,并且其与m无关.
1.2 线性贝叶斯反演
基于贝叶斯理论,模型参数的后验概率分布函数如下所示:
(7)
其中,p(m)表示模型参数的先验概率分布函数,p(d|m)为似然函数,p(d)是归一化常数,p(m|d)表示模型参数的后验概率分布函数.
线性正演算子G表示为
G=WAD,
(8)
由于噪声项e遵循高斯分布,而正演算子G是线性的,因此似然函数也遵循高斯分布.
先验概率分布函数和似然函数表示如下:
(9)
(10)
将式(9)、(10)代入式(7),可得:
(11)
对式(11)取对数,并令其对m求导,当其导数为0时,求得的m则为后验均值解.为了便于理解,对后验均值解的解析式进行变形,同时推导得到后验协方差的解析式(Buland and Omre, 2003; Tarantola, 2005).公式如下所示:
(12)
其中,μm|dobs和Cm|dobs分别为后验均值和后验协方差矩阵;dobs为观测地震数据.
为了说明Δα/α,Δβ/β,Δρ/ρ等参数数对纵波地震响应的影响,对以上参数做微扰分析.图1分别显示了纵、横波速度和密度对纵波反射振幅的扰动影响.图1中的参数从-0.3变为0.3,间隔为0.15.从图1可知,纵、横波速度和密度对反射系数的贡献都与入射角有关,并且纵波速度对反射系数的贡献较大.
1.3 碎屑岩岩石物理模型
物性参数的反演与岩石物理模型的选取密切相关,本文选取Gassmann方程和临界孔隙度模型针对碎屑岩进行岩石物理建模,碎屑岩主要成分为石英和黏土.模型建立流程如图2所示.
Voigt-Reuss-Hill平均公式为
(13)
式中:Kc是泥质的体积模量,Gc是泥质的剪切模量;Kq是石英的体积模量,Gq是石英的剪切模量;C表示泥质含量;Km和Gm分别是通过Voigt-Reuss-Hill平均公式计算得到的岩石基质的体积模量和剪切模量.
当获得岩石基质的体积模量和剪切模量时,岩石骨架的体积模量和剪切模量可以通过临界孔隙度模型计算得到:
(14)
式中:Kdry是岩石骨架的体积模量;Gdry是岩石骨架的剪切模量;φ是孔隙度;φc表示临界孔隙度,一般取经验值.
通过各向同性Gassmann方程进行流体替换,可以将岩石骨架的模量转化为饱和岩石的模量:

图1 弹性参数敏感性分析(a) 纵波速度; (b) 横波速度; (c) 密度.

图2 碎屑岩岩石物理建模流程图
式中:Ksat是饱和岩石的体积模量;Gsat是饱和岩石的剪切模量;Kf是饱和流体的体积模量.
饱和流体的体积模量和密度计算公式如下:
(16)
式中:Sw是含水饱和度;Khc是气体的体积模量,Kw是水的体积模量;ρw是水的密度;ρhc是气体密度;ρf是饱和流体的密度.
最终,可以得到饱和岩石的纵波速度α、横波速度β和密度ρ:
(17)
(18)
ρ=ρm(1-φ)+ρfφ.
(19)
为了说明物性参数φ、C和Sw对弹性参数的影响,利用建立的碎屑岩岩石物理模型进行正演模拟分析.假设岩石基质主要成分为石英和黏土,孔隙流体为气水混合,对应的模量和密度如表1所示.

表1 岩石物理模型相关参数Table 1 Parameters of the rock-physics model
岩石物理正演模拟分析如图3所示,从图3a中可知,弹性参数随着孔隙度的增加而变小,纵波速度和横波速度随孔隙度的递增是一种非线性递减的趋势.图3b显示弹性参数随着泥质含量的增加而变小,并且纵、横波速度与泥质含量其非线性关系比较弱.图3c显示纵、横波速度随着含水饱和度的增加整体上变化不大,密度随含水饱和度的增加而变大.由图3可知,弹性参数对于孔隙度最敏感,泥质含量次之,含水饱和度又次之.
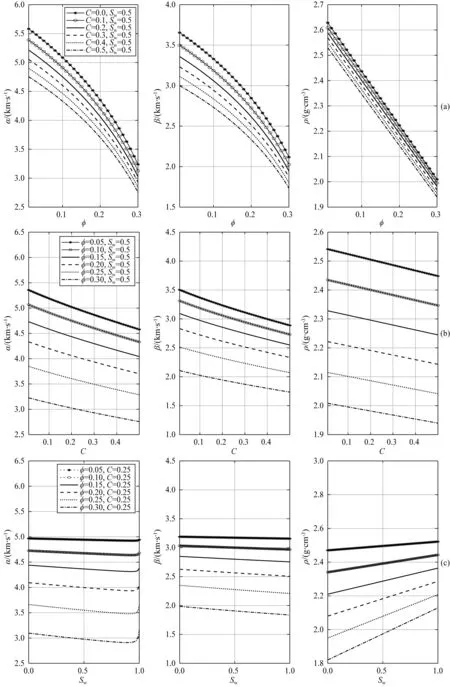
图3 物性参数敏感性分析(a) 孔隙度; (b) 泥质含量; (c) 含水饱和度.
1.4 基于粒子群算法的岩石物理反演
岩石物理模型具有非线性特征,本文采取粒子群算法进行岩石物理反演获取储层物性参数.粒子的状态用位置和速度来表示,每个粒子都有其初始速度和初始位置,粒子通过更新速度和位置来进行寻优,最优解求解过程则简化为这些粒子搜寻最佳位置的过程.表达式为
(20)

通过适应度函数得到粒子的个体最优解和全局最优解,进而通过扰动进行粒子速度和位置的更新.表达式为
(21)

粒子群算法过程如下所示:

输入:迭代次数T;种群规模N;问题维度D输出:全局最优解x*(t)1 设置t=1,i表示粒子编号,j表示维度2 粒子初始位置和速度:xji=xmin+rand(xmax-xmin),vji=xji/1003 利用适应度函数计算粒子适应度值,得到个体最优解和全局最优解4 While t≤T5 fori=1 to N6 fori=1 to D7 vji(t+1)=wvji(t)+c1rand(pbestji(t)-xji(t))+c2rand(gbestj(t)-xji(t));8 xji(t+1)=xji(t)+vji(t+1);9 限制粒子速度和位置的扰动上下限10 计算新的个体最优解和全局最优解11 end12 end13 t=t+1;14 end15 return x*(t)
2 合成数据测试
本文对测井数据所生成的合成地震数据进行测试,验证了所提方法的可行性和稳定性.测井数据包括物性参数孔隙度、泥质含量和含水饱和度,然后基于构建的岩石物理模型由物性参数正演得到纵、横波速度和密度等弹性参数.图4显示了纵波反射系数和主频为35 Hz的雷克子波相褶积得到的合成地震角度道集,为了说明反演方法具有一定抗噪性,在无噪声合成地震道集的基础上添加信噪比(SNR)为2的高斯噪声.
从合成地震角道集中提取入射角分别为5°、15°、25°所对应的角道集,然后利用线性贝叶斯AVO反演方法得到模型参数m的后验分布显式解析式,进而得到纵、横波速度和密度的反演结果并分析其不确定性.图5是使用无噪声合成地震道集反演得到的弹性参数,其中蓝色曲线指示初始模型,黑色曲线为测井曲线,红色曲线表示反演结果,红色虚线表示95%的置信区间,背景颜色表示后验分布.图5显示纵、横波速度和密度的反演值与真实值吻合良好.图6是使用信噪比为2的合成地震道集得到的反演结果,图6表明当地震数据含有一定噪声时,反演值与真实值仍然有较好的一致性,这说明所提方法具有抗噪性.除此以外,从图5和图6可知,后验概率分布显示了反演结果的可靠性,反演结果有95%的概率在红色虚线范围内.线性贝叶斯反演方法有助于评价反演结果的不确定性,这可以为地震解释提供更多有用的参考消息.
利用皮尔逊公式计算的相关系数如表2所示,从表2可知纵、横波速度的反演效果优于密度,当信噪比从无噪声变为信噪比为2时,反演得到的弹性参数的相关系数略有下降.反演结果表明即使加入增加一些噪声,估测值与真实值仍然具有很好的一致性,验证了线性贝叶斯反演方法的可行性与稳定性.
基于弹性参数的反演结果,可以利用粒子群算法进行岩石物理反演以估测储层物性参数.本文选取的惯性权重为wmax-(wmax-wmin)×(t/T)2,以无噪声情况为例,本文对粒子群算法的反演效率进行分析如图7所示.从图7a可知,算法运行时间随着迭代次数的增加而增加,然而在迭代次数相同时选取不同的惯性权重对于粒子群算法的运行时间影响不大.图7b表明迭代次数相同时本文方法具有更高的反演精度,图7c表明本文方法具有更快的收敛速度,在迭代3000次时适应度值已经收敛,其运行时间为145.61 s,选取的惯性权重反演效果优于另外两者.综上,本文方法具有较高的反演效率.
表2 不同噪声水平下估测值与真实值之间的相关系数Table 2 The correlation coefficients between estimated values and true values with different noise levels

图4 不同噪声下的合成地震记录角道集
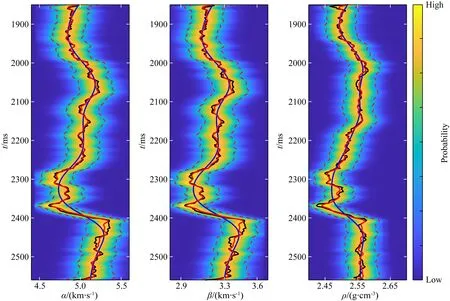
图5 基于线性贝叶斯反演得到的纵、横波速度和密度的后验分布(无噪声)
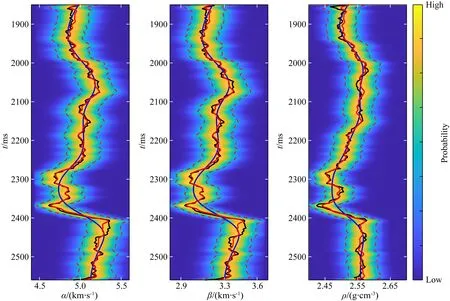
图6 基于线性贝叶斯反演得到的纵、横波速度和密度的后验分布(信噪比为2)
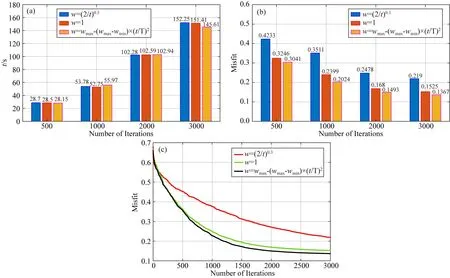
图7 粒子群算法反演效率分析,以无噪声情况为例(a) 不同惯性权重下运行时间随迭代次数的变化; (b) 不同惯性权重下适应度值随迭代次数的变化; (c) 不同惯性权重下的收敛曲线.

图8 孔隙度、泥质含量和含水饱和度反演结果(无噪声)

图9 孔隙度、泥质含量和含水饱和度反演结果(信噪比为2)
利用粒子群算法进行储层物性参数反演,并将其与线性化反演方法进行对比.图8是无噪声情况下反演得到的储层物性参数,图9是含噪反演结果,其中黑色曲线表示测井数据,黑色虚线表示将岩石物理模型线性化后得到的反演结果,黑色点线表示粒子群算法反演结果.从图8和图9可知,粒子群算法得到的反演结果优于线性化反演结果,并且反演得到的孔隙度、泥质含量和含水饱和度与测井数据拟合良好.此外,图8和图9表明孔隙度和泥质含量的反演效果要优于含水饱和度.图9表明由于加入了噪声,物性参数的反演效果略有下降,然而反演结果与测井数据仍然有较高的吻合度,验证了粒子群算法具有一定抗噪性.
利用均方根误差分析弹性参数反演误差对由粒子群算法得到的物性参数反演精度的影响,弹性参数和物性参数的均方根误差如表3所示.从表3可知,纵、横波速度和密度的含噪声反演结果的均方根误差相较于无噪声反演结果略有增加,并且弹性参数反演误差的增加会导致物性参数反演精度的下降.因此,为提高物性参数的反演精度应尽可能保证弹性参数反演的准确性.

表3 不同噪声水平下弹性参数和物性参数的均方根误差Table 3 Root-mean-square error of elastic and physical parameters with different noise levels
3 实际数据测试
接下来,为进一步验证所提出的岩石物理驱动的储层物性参数非线性地震反演方法的可行性、稳定性和实际应用效果,利用一组来自中国西南部某地区的实际数据集对其进行测试.实际工区构造位置上位于四川盆地某坳陷中段大型隆起带西端,构造上属于南陡北缓,存在一定断层发育.地层碎屑物以砂岩为主,同时含有泥岩等岩屑成分,砂岩主要为细-中粒砂岩,成熟度较高,因此目标储层为碎屑岩储层.通过钻井、录井以及测井综合解释可得储层以产水及产气为主,因此流体为气水混合.通过测井解释获取的储层参数可以较为真实地反映实际地层地质特征,但同时有必要对实际工区开展地震储层预测及评价.所用实际数据包括叠前地震数据和实际测井数据.图10显示了入射角度分别为15°、22°和29°的地震数据,地震剖面一共有328道数据,测井数据其钻井位置位于第224道处.
图11是通过线性贝叶斯反演方法得到的弹性参数,图中的黑色曲线表示测井曲线.可以看出,反演结果具有较高的分辨率和良好的横向连续性,并且反演剖面中可以显示一些丰富的细节特征.图11显示反演得到的弹性参数剖面与实际测井数据吻合性较好,验证了反演结果的准确性.此外,图11中红色椭圆区域表示含气储层位置,在含气储层处反演得到的纵、横波速度显示为低值,密度略有下降.
通过后验标准差可以评估反演得到的弹性参数的不确定性,标准差越大即表明反演结果的不确定性越大.纵、横波速度和密度的后验标准差剖面如图12所示,从图12可知后验标准差整体上远小于弹性参数值,显示了反演结果的可靠性并指示了其不确定性.对于后验标准差较大的区域,说明需要提高该区域反演结果的可靠性,这为后续有针对性地提高反演精度指明了方向.线性贝叶斯反演方法可以分析弹性参数反演结果的不确定性,这是传统的确定性反演方法所不具有的优点.
为进一步说明弹性参数反演结果的准确性,将井旁道反演结果与测井曲线进行比较.比较结果如图13所示,其中黑线实线是测井曲线,黑线虚线是反演结果.图13显示反演得到的纵、横波速度以及密度与测井曲线拟合较好,整体变化趋势是相同的,验证了线性贝叶斯反演方法的可行性和准确性.
利用图11中的弹性参数基于粒子群算法进行储层物性参数反演,图14a—c分别是反演得到的孔隙度、泥质含量和含水饱和度.图14中的黑色曲线表示测井曲线,从图14中可知反演得到的物性参数剖面与实际测井数据吻合性较好,验证了反演结果的准确性.孔隙度和泥质含量的反演效果要优于含水饱和度,这是由于含水饱和度对弹性参数的贡献度比较小.图14中红色椭圆区域表示含气储层位置,在含气储层处反演得到的孔隙度显示为高值,泥质含量和含水饱和度显示为低值,物性参数反演结果与测井解释结果相符合.图15将井旁道反演结果与测井曲线进行对比,其中黑线实线是测井曲线,黑线虚线是反演结果.图15表明反演得到的孔隙度、泥质含量和含水饱和度与测井曲线具有较好的一致性,验证了粒子群算法在物性参数反演中的可行性和准确性.
最后,将所提出的方法应用于实际三维地震数据集,以验证该方法的适用性.三维数据Xline测线范围为1149~1419,Inline测线范围为2400~2700,对应的时间范围为2150~2736 ms.图16显示了入射角度分别为15°、22°和29°的三维地震数据中的2条测线,分别为Xline1308测线和Inline2606测线.根据测井解释结果,Inline2606测线第119道、2550 ms处存在一处高孔隙度的碎屑岩.

图10 二维实际地震数据(a) 小角度叠加道集,平均角度为15°; (b) 中角度叠加道集,平均角度为22°; (b) 大角度叠加道集,平均角度为29°.

图11 弹性参数二维反演结果(a) 纵波速度; (b) 横波速度; (c) 密度.

图12 弹性参数后验标准差剖面(a) 纵波速度标准差; (b) 横波速度标准差; (c) 密度标准差.
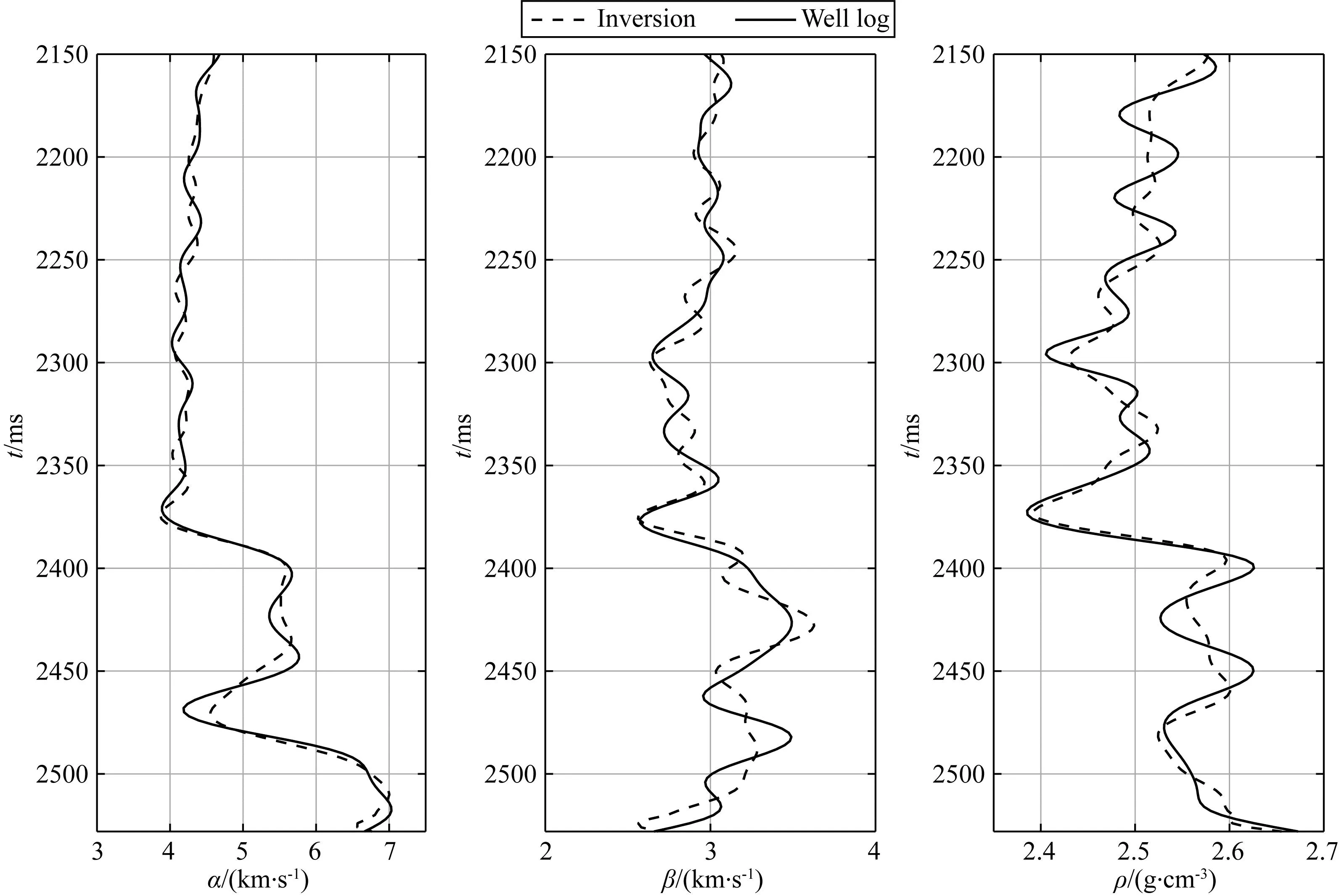
图13 井旁道弹性参数反演结果与测井曲线比较

图14 物性参数二维反演结果(a) 孔隙度; (b) 泥质含量; (c) 含水饱和度.

图15 井旁道物性参数反演结果与测井曲线比较
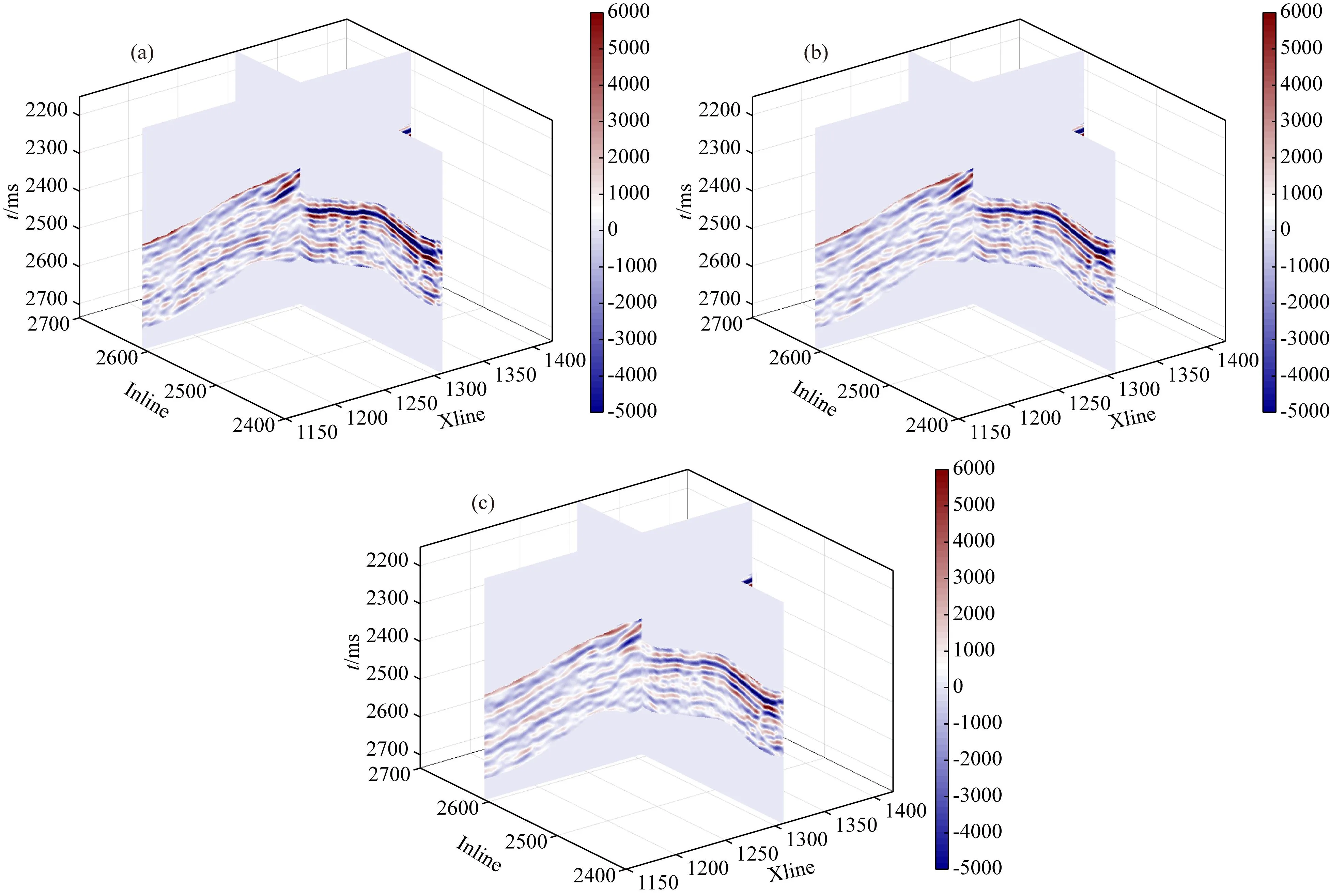
图16 三维实际地震数据(a) 小角度叠加道集,平均角度为15°; (b) 中角度叠加道集,平均角度为22°; (c) 大角度叠加道集,平均角度为29°.

图18 物性参数三维反演结果(a) 孔隙度; (b) 泥质含量; (c) 含水饱和度.
弹性参数三维反演结果如图17所示,物性参数三维反演结果如图18所示,黑色箭头所指位置即为储层位置.反演结果可以较为准确的描述含气储层的空间分布,储层位置处的孔隙度存在高值异常,并且泥质含量和含水饱和度存在低值异常.三维实际数据测试结果表明所提方法在三维工区同样具有较好的应用效果.
4 结论
针对储层精细表征和物性参数反演问题,为了有效实现储层预测及评价,本文主要研究了岩石物理驱动的储层物性参数非线性地震反演方法.首先基于贝叶斯框架和高斯分布约束条件,从叠前地震数据中反演得到纵、横波速度及密度等弹性参数;继而基于建立的非线性碎屑岩岩石物理模型,应用粒子群算法实现了孔隙度、泥质含量和含水饱和度的反演.主要结论和认识如下:
(1)基于线性贝叶斯AVO反演方法,利用褶积模型和贝叶斯理论推导了弹性参数后验均值和后验协方差的解析式,可实现弹性参数的有效估测及反演结果的不确定性分析.合成数据和实际数据测试结果表明弹性参数反演结果和测井数据吻合良好,同时弹性参数可对含气储层区域进行一定指示.
(2)利用Gassmann方程和临界孔隙度模型建立了非线性的碎屑岩岩石物理模型,应用粒子群算法实现了孔隙度、泥质含量和含水饱和度的反演,克服了将岩石物理模型线性化导致的局限性,避免了对初始模型的过度依赖;实际数据测试结果表明物性参数反演结果和测井数据具有较好的一致性,反演得到的物性参数可有助于储层评价及精细表征,在含气储层位置处孔隙度显示为高值,泥质含量和含水饱和度显示为低值,反演结果与测井解释结果相符合.
(3)将所提方法应用于三维勘探工区,反演结果可以较为准确地描述含气储层的空间分布,测试结果表明所提方法在三维工区同样具有较好的应用效果.
岩石物理驱动的储层物性参数非线性地震反演方法可实现物性参数的反演,并且将弹性参数和物性参数相结合可更好地用于识别储层并进行有效的储层评价.本文方法也存在一定局限性,为了缓解AVO反演的不适定性,纵波反射系数公式是一个线性近似式而不是精确式,因此弹性参数的反演精度略有下降;除此以外,我们对模型参数的先验分布做了限制性假设,假设模型参数服从高斯分布;此外,研究内容没有考虑存在裂缝系统的复杂介质,后续将建立各向异性岩石物理模型,进一步考虑裂缝密度对各向异性岩石物理模型的影响,在通过地震各向异性反演实现弹性参数与裂缝相关参数准确估测的基础上,针对裂缝介质储层参数开展反演方法研究.
