ICESat-2水深提取方法及其反演应用
2024-03-11胡琪鑫程亮楚森森程俭徐亚
胡琪鑫, 程亮, 楚森森, 程俭, 徐亚
1 南京大学地理与海洋科学学院, 南京 210023
2 江苏省地理信息技术重点实验室, 南京 210023
3 中国科学院地质与地球物理研究所, 中国科学院油气资源研究重点实验室, 北京 100029
4 中国科学院大学, 北京 100049
0 引言
浅海水下地形数据作为海洋环境的基础地理信息数据,是海洋工程建设与海洋科学研究的重要支撑.在海洋工程建设方面,浅海水下地形广泛服务于航行安全(Mavraeidopoulos et al.,2017)、海上救援(Pelot et al.,2015)和资源勘探(Brando et al.,2009)等领域.在海洋科学研究方面,水下地形数据不仅是水动力学和波浪建模(O′Hara Murray and Gallego,2017;Khanarmuei et al.,2020)的重要输入参量和海岸带地貌与沉积物搬运研究(Kanari et al.,2020)的关键参考数据,还可以辅助海底底质分类与珊瑚礁栖息地绘图(Eugenio et al.,2015;Hedley et al.,2018)等.
当前常用的水深测量方法主要包括船载声呐(单波束、多波束、侧扫声呐等)测深,机载LiDAR(Light detection and ranging)测深和基于卫星影像的水深反演.其中,船载声呐测深精度高,测深能力强但费用昂贵,且在复杂地形或极浅水域难以开展工作;机载LiDAR测深精度和效率高,适用于极浅水域,但依旧存在费用昂贵、不适合大范围测深的缺点(Kotilainen and Kaskela,2017);基于卫星影像的水深反演研究兴起于1972年美国发射的第一颗陆地资源卫星Landsat-1,其优点是不受地域限制,覆盖面积大,费用低且获取方便;缺点是被动光学信号微弱,易受环境影响,精度较低,且大多数经验统计反演模型仍然需要其他手段的测深数据作为训练样本.近年来,随着搭载主动激光测高系统的卫星陆续升空以及对其水下测深能力的验证(Neumann et al.,2019;Parrish et al.,2019),结合主动激光测深与被动光学影像的主被动融合水深反演成为大范围、低成本获取浅海水下地形的主流研究方向.
ICESat-2光子点水深提取主要包括海面、海底光子点群提取和光子点水深值改正三部分内容.目前,ICESat-2海面、海底光子点群提取方法大多借鉴于传统的机载光子云数据处理算法,主要包括基于栅格图像处理的提取方法,基于空间滤波的提取方法,基于分布统计特征的提取方法和基于密度空间聚类的提取方法.(1)基于栅格图像处理的提取方法将光子点云转换为栅格图像然后对其作去噪或滤波处理,原理简单,但在转换过程中容易损失部分精度(Chen and Pang,2015);(2)基于空间滤波的提取方法如基于体素的空间滤波(Tang et al.,2016),主要适用高信噪比的光子点云数据,难以适用于高背景噪声的ICESat-2数据;(3)基于分布统计特征的提取方法对光子点云的空间分布进行局部或全局的特征统计,利用统计特征差异区分信号点和光子点,如局部距离统计(夏少波等,2014)、窗格统计(Popescu et al.,2018)、直方图统计(Hsu et al.,2021;Ranndal et al.,2021)等,基于分布统计特征的提取方法精度高,效果明显,但仍然不足以应对海底光子点群信噪比低、分布场景多样化的特点;(4)基于密度空间聚类的提取方法主要有贝叶斯、OPTICS(Ordering Points to Identify the Clustering Structure)、DBSCAN(Density-Based Spatial Clustering of Applications with Noise)三种,目前应用最为广泛的是DBSCAN及其改进算法,DBSCAN算法对扫描半径和最小包含点数两个参数极其敏感,基于DBSCAN的改进算法主要解决参数寻优的问题,如基于距离矩阵的候选集寻优(Ma et al.,2020;Xie et al.,2021)、基于点云自身分布特性的K-平均最近邻寻优(孟文君等,2021)、基于聚类分析的自适应寻优等(秦磊等,2020).目前,基于DBSCAN及其改进的提取方法在海底光子点群提取中具有较好的提取结果,但均未考虑光子点密度随深度的变化特点,且在不同轨迹长度、海面起伏度的海面光子点提取场景中适用性较差.
提取海面和海底光子点后,需要对光子点水深值进行地球物理改正和水体折射改正.目前,应用最广泛的水体折射改正模型是Parrish等(2019)基于Snell折射定律提出的水体折射改正几何模型,其他模型均是基于Parrish模型的改进或简化模型,如Ma 等(2020)在Parrish模型的基础上考虑海面波浪造成的高程差异、Hsu等(2021)基于Parrish模型统计分析结果得到简化经验模型等.水体折射改正是光子点水深改正项中数量级最大的改正项,而现有的改正模型均未考虑海面倾斜造成的入射角偏移.
1 研究区与数据源
1.1 研究区概况
如图1所示,本研究选取两个典型的珊瑚礁作为研究区,分别为位于澳大利亚GBR(Great Barrier Reef)中部的John Brewer Reef 和南部的Fitzroy Reef.研究区水质清澈,叶绿素和悬浮物浓度低,含有丰富的珊瑚、沙石、藻类等底质.John Brewer Reef实验区位于澳大利亚昆士兰州Townsville市东北约38海里处,地理范围为18.66°S—18.61°S、147.02°E—147.08°E,总面积约38.97 km2.John Brewer Reef是一个约6 km宽的巨大裸露中陆架礁石,由西南向东北方向延伸,水深呈现从东南到西北逐渐变浅的趋势,最深处达≥18 m.受气候变化和人类活动的影响,John Brewer Reef珊瑚白化现象严重,现已处于地质年龄的衰老阶段.为此,英国雕塑家和海洋保护主义者Jason DeCaires Taylor在其东北角修筑了深达18 m的人工构筑物群——Museum of Underwater Art(MOUA),用以警示人类保护海洋环境.Fitzroy Reef实验区位于澳大利亚昆士兰州Seventeen Seventy镇东北约32海里处,地理范围为23.64°S—23.60°S、152.12°E—152.19°E,总面积约38.04 km2.Fitzroy Reef是Bunker Group中最大的干燥封闭环礁,拥有极其丰富的珊瑚、鱼和海龟种类.Fitzroy Reef礁盘内存在大量水深低于6 m的区域,周围礁脊至深海区域水深变化剧烈,中部为GBR南段唯一自然形成的全潮汐入口泻湖,最深处达≥10 m.
1.2 数据源
1.2.1 ICESat-2 ATL03光子点
美国国家航空航天局(National Aeronautics and Space Administration, NASA)于2018年9月发射成功的冰、云与陆地高程卫星二号(Ice, Cloud, Land Elevation Satellite-2, ICESat-2)搭载了先进地形激光测高系统(Advanced Topographic Laser Altimeter System, ATLAS),ATLAS的主要构成是一台激光波长为蓝绿波段(532 nm)的光子计数激光雷达,可实现全球海拔高度监测.ATL03数据集,即全球定位光子点(Global Geolocated Photons),是ICESat-2数据集的一个子集,数据级别为Level 2.研究选取ATL03 2021年11月发布的最新Version 5产品,ATL03 V5更新了与光子点往返时间相关的测距误差改正.本研究从EARTHDATA(https:∥search.earthdata.nasa.gov/search)获取了两个研究区自2018年10月13日至2022年6月30日的所有数据,为获取经过研究区的所有轨迹条带,设置范围经纬度方向分别外扩0.2°,分别获得96、109个项目文件,数据量分别为5.06、5.73 GB.
1.2.2 Sentinel-2多光谱影像
Sentinel系列卫星是欧盟委员会和欧洲航天局(European Space Agency, ESA)提出的全球环境与安全监测系统项目(“哥白尼计划”)的专用卫星系列.其中,Sentinel-2用于陆地监测,可提供植被、土壤和水覆盖、内陆水路及海岸区域等图像,还可用于紧急救援服务.Sentinel-2现阶段在轨运行卫星包括Sentinel-2A和Sentinel-2B两颗同高度轨道、相位相差180°的卫星,分别于2015年6月23日和2017年3月07日发射成功,Sentinel-2C计划于2024年发射.Sentinel-2的主要有效载荷为一枚多光谱成像仪(Multispectral Imaging ,MSI),在可见光/近红外(VNIR)和短波红外光谱范围(SWIR)中具有13个光谱通道.Sentinel-2卫星提供的数据产品包括Level-1B、Level-1C、Level-2A,其中,Level-1B为原始数据,需要专业的校正技术;Level-1C是经过辐射校正和几何校正的大气上层表观反射率产品.本研究基于GEE(Google Earth Engine:https:∥earthengine.google.com)获取了两个研究区自2018年1月1日至2022年6月30日所有云量像素百分比低于10%的Sentinel-2 L1C影像并进行空间裁剪和波段选择,最终通过重新计算更为精确的云量分数并排序,两个研究区最佳影像分别选定为John Brewer Reef: 20190822时相和Fitzroy Reef: 20180902时相,影像大小分别为2.70 MB、2.54 MB.
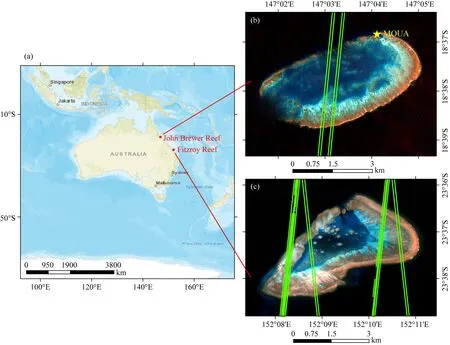
图1 研究区与数据源(a)John Brewer Reef 和Fitzroy Reef 的地理位置;(b)、(c)John Brewer Reef、Fitzroy Reef的Sentinel-2影像(彩色背景)与ICESat-2轨迹(绿色条带)((b)中黄色星号代表MOUA)
2 ICESat-2光子点水深提取方法
2.1 ICESat-2 ATL03数据预处理
针对ICESat-2数据量大但有效信息占比并不高的特点,对ICESat-2原始H5格式数据做文件重命名、有效信息存储、空间裁剪、高程截取、无效文件去除等数据预处理.ICESat-2 ATLAS的理论最大测深深度约为40 m以浅,已有实例区域测深能力为约1个Secchi深度(Tyler,1968).因此,本文利用Isolation Forest异常点检测算法(Liu et al.,2008)初步确定海面点平均高程,截取海面高程下50m至海面高程上5m的光子点.预处理后,两个研究区分别保留了4、18条包含有效海底光子点的波束条带,如图1.如表1所示,每条波束条带轨迹分别提取每个光子点的时空定位与信号水平信息(/gtx/heights: delta_time、lon_ph、lat_ph、h_ph、dist_ph_along、signal_conf_ph)、地球物理改正项信息(/gtx/geophys_corr: dac、tide_earth、tide_load、tide_ocean、tide_equilibrium、tide_oc_pole、tide_pole)和分段地理信息(/gtx/geolocation: segment_id、ref_azimuth、ref_elev)并以波束条带为基本单元保存为CSV文件.

表1 ATL03 V5 字段含义Table 1 Field meanings of ATL03 V5 dataset
2.2 基于光子点群高斯分布特征的海面光子点群提取方法
(1)滑动窗口设置:ATL03 V5 波束条带轨迹长度从几千米到几万米不等,当处理窗口大小过小时,光子点数量较少可能造成高斯分布不明显;当处理窗口大小过大时,海面高程可能出现较大起伏造成双峰拟合偏离;经试验,设置滑动窗口大小和步长均为10000 m时,可以较好地提取出代表海面光子点的高斯主峰.
(2)分段双重高斯拟合:统计计算滑动窗口内的所有光子点高程分布直方图,直方图中高程区间宽度采用Freedman-Diaconis准则(Freedman and Diaconis,1981).Freedman-Diaconis准则基于最小化直方图和理论概率分布密度之间平方差的积分和,可以根据数据分布确定合适的区间宽度,具备良好的抗噪性.对光子点高程分布直方图进行双重高斯拟合,双重高斯模型概率密度函数如下:
(1)
其中,α1,α2为振幅,μ1,μ2为期望,σ1,σ2为标准差.设定当双重高斯拟合标准差最大值≥0.95或期望值之差<0.3时,则判定双重高斯分布不明显,用单高斯模型代替进行重新拟合.高斯拟合后的主峰期望即为平均海面高程,选取高程范围[μ-3σ,μ+3σ]的光子点作为该分段的海面候选光子点.滑动循环重复此步骤,即可得到波束条带轨迹内的所有海面候选光子点,得到海面候选光子点集.
(3)尺度缩放:海面候选光子点轨迹方向点间距和高程方向点间距存在明显不平衡的尺度差异,为利于下一步DBSCAN聚类,将海面候选光子点轨迹方向距离作1/3缩放处理.
(4)DBSCAN聚类去噪:与基于距离的聚类算法不同,DBSCAN作为基于密度空间聚类算法中的经典算法,具备区分出非球状复杂形状簇并找出不属于任何簇的噪声点的能力和优势(Ester et al.,1996;Khan et al.,2014).本文采取滑动窗口分段处理的策略对海面候选光子点作DBSCAN去噪,设置滑动窗口大小和步长分别为100 m和50 m.DBSCAN聚类涉及邻域的距离阈值eps和样本点数量阈值min_samples两个参数,本文利用sklearn.optimize模块实现该算法,设置eps=1,min_samples=4.
2.3 基于深度自适应DBSCAN的海底光子点群提取方法
提取海面光子点群后,去除海面光子点候选集,在海面光子点候选集以深的地方设置0.2m的深度缓冲区,将缓冲区下的剩余光子点作为海底光子点群提取的输入数据.深度自适应的DBSCAN海底光子点群提取算法的具体步骤如下:
(1)尺度缩放:同海面光子点分布类似,海底光子点空间分布轨迹方向和高程方向存在尺度差异,为与DBSCAN算法的聚类原理一致,将轨迹方向距离范围缩放至与高程方向范围一致,缩放比例通过如下公式计算:
(2)
其中,xmax,xmin分别为沿轨迹方向距离最大、最小值,hmax,hmin分别为高程最大、最小值,r为轨迹方向距离缩放因子,xr为缩放后的轨迹方向距离.
(2)深度自适应分段:引入hwin、hstep两个参数分别控制深度分段窗口大小和步长,对每个深度段光子点的轨迹距离分布做Kolmogorov-Smirnov(KS test)(Massey,1951)均匀分布检验,KS test假设检验的置信度水平阈值设为:返回值statistic<0.1且pvalue>0.05时,则认定该深度段光子点轨迹距离分布符合均匀分布,该段深度段无海底光子点,对其不做处理.
(3)轨迹方向分段:对不符合均匀分布假设深度段的光子点做轨迹距离方向分段处理,引入xwin、xstep两个参数分别控制轨迹方向距离分段窗口大小和步长.同(2)对每个分段做KS test 非参数检验,置信度水平阈值不变,对符合假设的分段不做任何处理.
(4)距离矩阵和DBSCAN候选eps集确定:对不符合均匀分布的分段,计算分段内光子点间轨迹方向的距离,形成一个N×N的距离矩阵:DN×N={dist(i,j)|1≤i≤N,1≤j≤N},其中N为分段内的光子点总数.对距离矩阵的每行分别升序排列,则每行的第1列元素均为0,第k列元素代表每个点的k近邻距离Dk,所有行Dk的均值即组成候选的eps集epsN={epsk|1≤k≤N}.
(5)信号/噪声分块:将步骤(3)后的分段进一步在轨迹方向上分成M块,则分段光子点的块密度为
(3)
统计M块中光子点数大于ρ的块数M1以及M1块的光子点总数N1,将这些块标识为以信号光子点为主导的块,则以噪声光子点为主导的块数和光子点总数为
M2=M-M1,
(4)
N2=N-N1.
(5)
(6)候选min_samples集确定:依次对epsN中的每个候选epsk按照下式计算分段内以epsk为半径的圆内的总平均光子点点数Nall和噪声为主导的平均光子点数:
(6)
(7)
其中,h′max,h′min为分段内的光子点高程最大、最小值,x′rmax,x′rmin为分段内光子点尺度缩放后轨迹距离的最大、最小值.最后,依据下式即可计算得到每个候选epsk对应的候选min_samples:
|1≤k≤N},
(8)
(7)迭代确定最优epsopt和min_samplesopt参数:从k=1开始按照升序依次将对应的epsk、min_samplesk代入DBSCAN算法对分段内光子点进行聚类,当聚类类别数连续三次不变时,最后一次DBSCAN的聚类参数即为最优参数epsopt和min_samplesopt.
(8)DBSCAN最优参数聚类:按照最优参数阈值epsopt和min_samplesopt对分段内光子点进行聚类,得到分段内海底光子点群.
(9)重复(2—8)步骤,即完成一次深度自适应DBSCAN算法聚类去噪.
(10)对每条波束轨迹条带做2次大尺度深度自适应DBSCAN聚类和1次小尺度深度自适应DBSCAN聚类(次数依据实际光子点分布状况调节),大尺度深度自适应DBSCAN聚类旨在去除远离有效海底光子点的大量噪声点,参数设置为:hwin=5,hstep=2.5,xwin=1,xstep=100000,M=100,而小尺度深度自适应DBSCAN聚类旨在去除有效海底光子点邻近的少量噪声点,提取更可靠的有效海底光子点,参数设置为hwin=2,hstep=1,xwin=100,xstep=50,M=50.
2.4 水深改正方法
2.4.1 地球物理改正
不同地球物理改正项作用的光子点群有所不同,且大部分改正已在ATL03中实现.因此,本文对光子点的地球物理改正实际包括(1)对海表光子点作动态大气改正(Dynamic Atmospheric Correction, DAC)与逆气压(Inverted Barometer, IB)效应改正;(2)对折射改正后的初步水深值作海洋潮汐改正.改正公式如下:
Dgc=R(Hbot-(Hsur-ΔHDAC))+Δd+ΔHtide_ocean
+ΔHtide_equilibrium,
(9)
其中,Dgc为水体折射改正和地球物理改正后的水深值,R(·)为折射改正函数,Hbot为提取的海底光子点高程,Hsur为提取的海面光子点高程,Δd为区域平均海平面与瞬时海面光子点的高程差.ΔHDAC,ΔHtide_ocean,ΔHtide_equilibrium分别为动态大气改正与逆气压效应改正项和海洋潮汐、均衡潮改正项.
2.4.2 水体折射改正
如图2所示,当波束以入射高度角φ入射时,由于海面波浪等影响,折射界面偏离水平,导致入射角θ1≠φ,且当瞬时海面与轨迹方向之间的倾角符号不同时,实际光子点与观测光子点之间的相对位置发生变化,最终导致折射改正计算公式不一.入射高度角φ可以从ATL03 V5数据集中的“ref_elev”字段计算得到,每个海底光子点对应海面倾角η利用轨迹方向邻近的5个点拟合直线求取.公式如下:
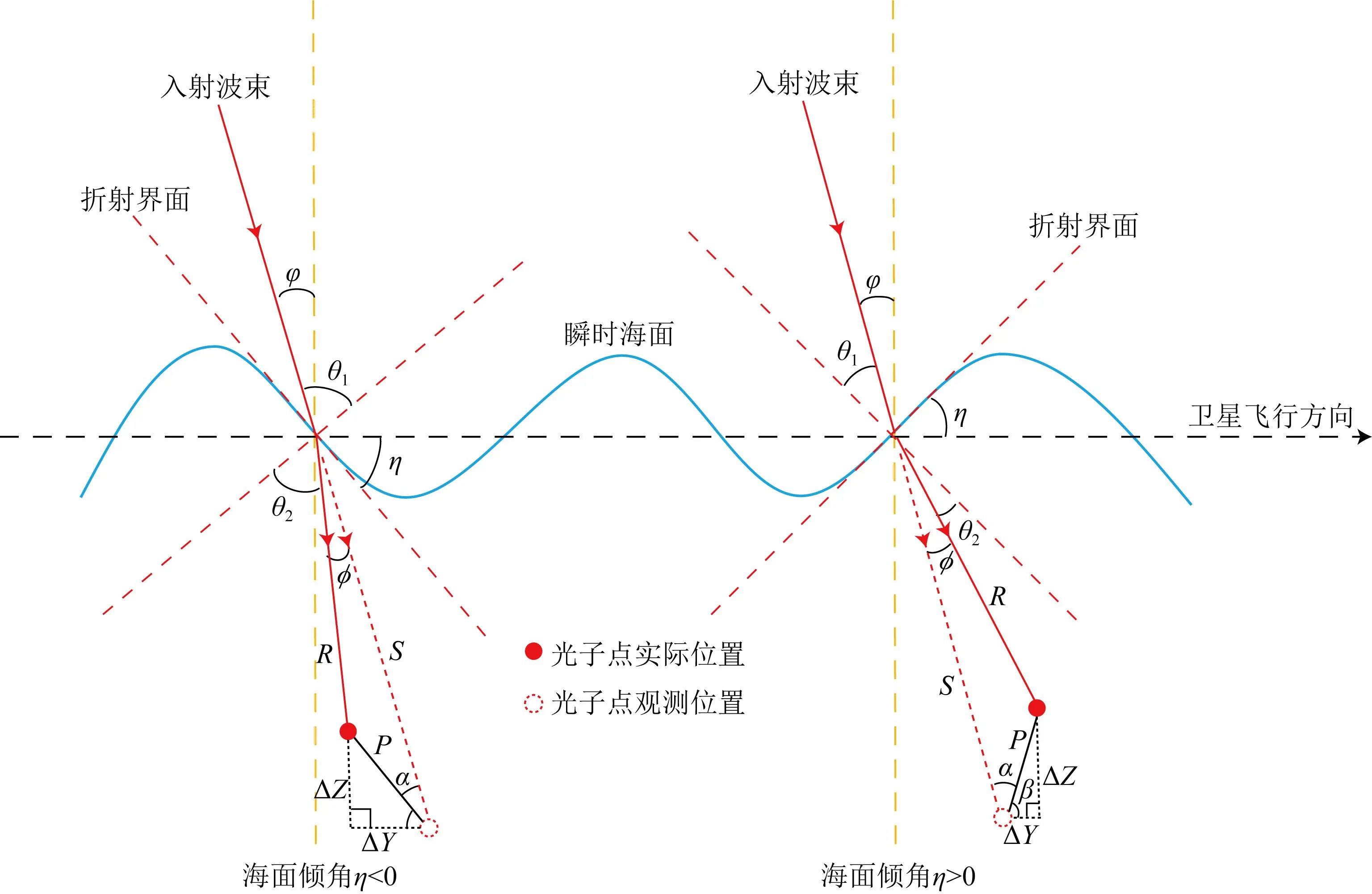
图2 折射改正几何模型
(10)
k=polyfit(neighbor(5)),η=arctan(k).
(11)
根据图2中的几何关系和Snell折射定律,入射角θ1和折射角θ2可由下式计算:
θ1=Abs(φ-η),
(12)
(13)
其中,na,nw分别为大气和海水折射率,na=1.00029,nw=1.34116.
同样地,由折射定律可以分别求得入射点到实际光子点和观测光子点间的距离R、S:
φ=θ1-θ2,
(14)
(15)
(16)
其中,φ为ΔRSP中边R和S之间的夹角,D=Hbot-(Hsur-ΔHDAC)为根据海面与海底光子点高程得到的初步水深值.求出φ,R,S后,改正距离P和R对应的角α可由余弦定理求出:
(17)
(18)
针对不同的η值,改正距离P的倾角β不同:
(19)
随即,每个海底光子点对应的水体折射改正项求解出:
ΔY=Pcosβ,
(20)
ΔZ=Psinβ,
(21)
其中,由于入射高度角非常小,在水深30 m时,ΔY≈9 cm,这相对于17 m波束足迹而言,可以忽略不计(Parrish et al.,2019),即只需加上水深方向的折射改正分量,得到折射改正后的光子点水深值Drc:
Drc=R(D)=D+ΔZ.
(22)
3 主被动融合水深反演方法
3.1 Sentinel-2影像预处理方法
(1)大气校正
为消除或减少大气分子、气溶胶的散射和臭氧、水汽等气体吸收对地物反射率的影响(Vermote et al.,2002),需要对下载的原始L1C级产品进行大气校正,将大气上层表观反射率转换为大气下层表观反射率.本文选用欧洲航天局官方最新发布的Sen2Cor 2.9插件对两个研究区的Sentinel-2 L1C 影像作批量化大气校正,Sen2Cor核心算法基于大气辐射传输模型libRadtran,相比于大气校正简化模型和6S(Second Simulation of a Satellite Signal in the Solar Spectrum)模型,拥有更高的精度和可靠性(苏伟等,2018).
(2)耀斑校正与空间域滤波
为削弱太阳耀斑噪声,本文采取Hedley等(2005)提出的耀斑校正方法对耀斑现象严重的影像进行校正,公式如下:
R(λi)sg=R(λi)-ki[R(λNIR)-min(R(λNIR))],(23)
其中,R(λi),R(λi)sg分别为耀斑校正前后可见光波段λi(i=blue,green,red)的遥感反射率值,R(λNIR)为近红外波段的遥感反射率值,ki为深水区R(λi)与R(λNIR)线性拟合的斜率,本文选择两个研究区影像的西北角100×100像元的区域作为深水区.为抑制遥感影像空间域噪声,以3×3像元的平滑窗口对耀斑校正后的遥感影像进行均值滤波.
(3)样本集生成与标准化
将提取的ICESat-2的水深点与处理后的遥感影像叠加,逐个遍历遥感影像10 m空间分辨率的所有像元,取单个像元内所有水深中值及其蓝、绿、红波段的反射率值作为水深反演实验的样本集,得到两个研究区水深样本总数分别为835、4701个,并以3∶7的比例在水深范围内随机均匀地抽取训练集和验证集,最终分别得到训练点、验证点250、585个和1410,3291个,如表2所示.为使水深反演不受样本集不同输入变量数量级不一致的影响,实验利用sklearn的StandardScalers对反射率值和水深值均进行标准差和取均值标准化处理.
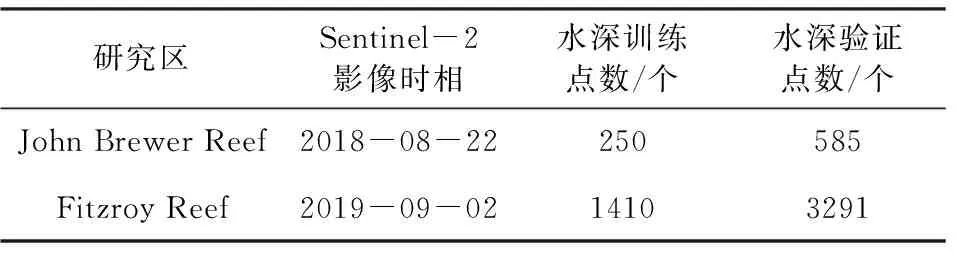
表2 水深反演样本集Table 2 Sample set of bathymetry inversion
3.2 水深反演模型
(1)单波段模型
单波段(Single Band, SB)模型以辐射传输方程为基础,利用光辐射通量沿水深的变化呈指数衰减的规律,建立影像可见光波段与水深的相对关系(Polcyn and Sattinger,1969),即:
R(λi)=R∞(λi)+airbie-kifz,
(24)
其中,R(λi)为可见光波段λi(i=blue,green,red)的反射率值,R∞(λi)为λi的深水区反射率值,ai,rbi,ki分别为反映波段λi太阳辐射、水体底部反射率和水体衰减对反射率影响的系数,f,z分别为水体路径长度和水深.由上式,可以得到水深关于反射率的关系:

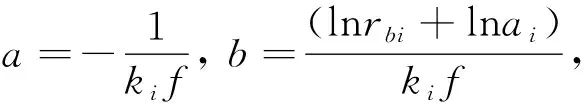
z=a(ln[R(λi)-R∞(λi)])+b,
(26)
单波段模型由辐射传输方程简化推导而来,回归系数a,b具备鲜明的物理意义.
(2)比值模型
Stumpf等(2003)在单波段模型的基础上,证明了利用不同波段之间的比值可以有效削弱水体和底质对水深反演的影响,并推导出水深反演的比值(Band Ratio, BR)表达式:
(27)
其中,R(λi),R(λj)为不同波段λi,λj的反射率值,一般取蓝、绿波段;m1,m0为模型参数,n为保证对数运算而设定的固定常数,一般取1000或10000(本文实验取1000).
(3)多项式模型
将单波段模型和比值模型扩展到多个波段,即得到Lyzenga多项式(Lyzenga Polynomial, LP)模型(Lyzenga,1978,1985):
(28)
其中,a0,ai(i=1,2,…,N)为拟合系数.基于Lyzenga一次多项式推广到更高阶的多项式即得到K阶多项式模型(滕惠忠等,2009;Paredes and Spero,1983):
(29)
ak1,k2,…,kN(i=1,2,…,N)为拟合系数,Xi=ln[R(λi)-R∞(λi)](i=1,2,…,N),通常K取2或3.
(4)支持向量回归模型
与Lyzenga多项式模型类似,Vojinovic等(2013)对比值算法作了非线性改进,利用支持向量机(Support Vector Machine)构建高维特征向量与水深之间的关系:
(30)
其中,f为非线性函数.对于非线性问题,支持向量回归(Support Vector Regression, SVR)模型使用核函数将输入变量隐式地转换到线性空间,核函数包括线性核函数、多项式核函数、sigmoid核函数、径向基核函数(Radial Basis Function, RBF)等,常用的径向基核函数如下式:
(31)
其中,xi,xj为特征向量.
(5)多层感知器模型
ANN根据神经元是否具有记忆功能分为前馈神经网络和后馈神经网络,其中,前馈神经网络也叫多层感知器(Multi-Layer Perceptron, MLP),它由输入层、若干隐藏层和输出层依次级联组成(Ceyhun and Yalçn, 2010),可由下式表达:
(32)
其中,oi,j+1为第j+1层的第i个神经元节点,om,j为第j层的第m个神经元节点,m=1,2,…,n,n为第j层的神经元节点数,wm,i为oi,j+1与上一次每个神经元节点om,j的连接权重,bi为偏移量,f为每一层的激活函数.在水深反演中,MLP的输入不需要对数运算处理,为可见光波段的反射率值.
(6)随机森林回归模型
随机森林(Random Forest, RF)是通过集成学习的Bagging思想将多棵决策树集成的一种算法,常用于多特征变量监督分类,同时还可以用来解决回归问题(Breiman,2001).同多层感知器模型一样,将随机森林回归模型运用至水深反演时,输入变量无需任何处理.随机森林回归模型参数设置为:决策树数量n_estimators=[50,100,150,200],分割准则选择均方误差和平均绝对误差criterion=[‘mse’,‘mae’],最大深度max_depth=[None,3,5,7,9,11],最小分割样本数min_samples_split=[2,4,6,8,10],最小叶子节点样本数min_samples_leaf=[1,2,3,4,5],同时采用bootstrap采样和袋外验证.
3.3 精度评价指标
为定量评价水深反演精度,本文采用均方根误差(Root Mean Squared Error, RMSE)、平均绝对误差(Mean Absolute Error, MAE)、平均绝对百分比误差(Mean Absolute Percentage Error, MAPE)、决定系数(coefficient of determination, r2_score)和Person相关系数(Pearson correlation coefficient)的平方R2共5个精度评价指标.各评价指标计算公式如下:
(33)
(34)
(35)
(36)
(37)

4 结果分析
4.1 ICESat-2水深提取
图3为Fitzroy研究区某轨迹条带上根据ATL03数据集提供的光子点置信度水平所作的空间分布和频数统计图,从中可以看到ICESat-2光子点分布具有如下几个特征:(1)高程方向明显的双高斯分布和有效光子点密度随深度减小特征;(2)海面光子点密度聚集的同时存在大量噪声点,且海面局部倾斜;(3)光子点置信度水平能够部分区分有效光子点与噪点,但依旧无法成为完整精确提取有效光子点群的有力凭据.而基于光子点高斯分布特征的海面光子点提取和基于深度自适应DBSCAN的海底光子点提取方法,能够依次提取出有效的海面和海底光子点群,去除大量噪声点.经过地球物理改正和折射改正后,光子点水深整体变浅,且越深的光子点水深值改正越大,如图4所示.
通过对两个研究区的所有有效光子点水体折射改正项和改正前水深进行线性回归分析,可以发现改正项与改正前水深呈强线性关系,如图5所示,回归系数为-0.2550,这与Parrish等的折射改正模型计算结果-0.25416十分接近,二者之间的差别由改进模型考虑海面倾斜造成.
4.2 主被动融合水深反演
4.2.1 水深反演结果
基于提取并生成的ICESat-2光子点水深与Sentinel-2影像反射率样本集,利用单波段(SB)、比值(BR)、Lyzenga多项式(LP)、二次多项式(Quadratic Polynomial, QP)、三次多项式(Cubic Polynomial, CP), 支持向量回归(SVR), 多层感知器(MLP)和随机森林回归 (RF)等8种水深反演模型在两个研究区分别开展主被动融合水深反演实验.基于以上8种不同模型,制作水下地形反演DEM(Digital Elevation Model)如图6、图7所示,除了SB模型和BR模型,其他6种模型均能反演出较为精细的水下地形,而SB模型和BR模型由于模型缺陷,水深反演结果整体偏浅,难以恢复深水区域的水下地形,如John Brewer Reef的东北角区域和Fitzroy Reef的西南角深水区域.

图3 Fitzroy_track0268_20191014_gt1l条带光子点分布和频数统计

图4 Fitzroy_track0268_20191014_gt1l条带光子点提取与改正后分布

图5 折射改正-水深线性回归图

图6 基于8种反演模型的John Brewer Reef水下地形图(a) 单波段模型; (b) 比值模型; (c) Lyzenga多项式模型; (d) 二次多项式模型; (e) 三次多项式模型; (f) 支持向量回归模型; (g) 多层感知器模型; (h) 随机森林回归模型.

图7 基于8种反演模型的Fitzroy Reef水下地形图(a) 单波段模型; (b) 比值模型; (c) Lyzenga多项式模型; (d) 二次多项式模型; (e) 三次多项式模型; (f) 支持向量回归模型; (g) 多层感知器模型; (h) 随机森林回归模型.

图8 John Brewer Reef实测水深与反演水深散点图(a) 单波段模型; (b) 比值模型; (c) Lyzenga多项式模型; (d) 二次多项式模型; (e) 三次多项式模型; (f) 支持向量回归模型; (g) 多层感知器模型; (h) 随机森林回归模型.

图9 Fitzroy Reef实测水深与反演水深散点图(a) 单波段模型; (b) 比值模型; (c) Lyzenga多项式模型; (d) 二次多项式模型; (e) 三次多项式模型; (f) 支持向量回归模型; (g) 多层感知器模型; (h) 随机森林回归模型.
4.2.2 模型预测表现分析
对验证集水深值和模型预测的水深值分布进行线性回归并绘制散点图,如图8和图9所示.综合两个研究区的水深反演结果发现:MLP、高阶多项式、RF模型的水深反演效果最好,在浅水和深水水域都拥有很好的反演表现,反演水深可达近30 m,其中MLP的表现最稳定;LP和SVR模型能较好地反演出0~30 m的水深,但在0~5 m的极浅水域和20~30 m的更深水域反演效果欠佳,这主要是受到模型复杂度不够或基于比值的基本原理所限制,复杂的非线性项可以更好地替代比值处理对底质影响的削弱作用;BR模型反演效果不稳定,在水深分布范围较窄的浅水区域反演结果尚可,但不具备深水反演能力,在样本点数更多水深范围更广的区域如Fitzroy Reef出现明显的深水区域预测更浅现象;SB模型反演表现最差,对水深与反射率关系的拟合能力最差,在实际的水深反演和水下地形产品生产中可用性较弱.
4.2.3 模型定量精度分析
进一步对两个研究区的训练集和验证集分别计算RMSE、MAE、MAPE、r2_score,定量评价不同反演模型的整体精度.如表3和表4所示,在John Brewer Reef研究区,RF模型训练集的拟合效果最好,训练集的RMSE=0.34 m,MAE=0.21 m,MAPE=3.19%,r2_score=0.99,但测试集的预测精度并非最高,这说明RF模型存在一定程度的过拟合;MLP、RF、多项式模型的整体反演精度最高,训练集和测试集精度均达到了RMSE<0.7 m,MAPE<0.5 m,MAPE<7%,r2_score≥0.97,其中高阶多项式模型比LP一次多项式模型精度更高;SVR、BR模型的反演精度次之,训练集和测试集精度均达到了RMSE<0.9 m,MAPE<0.65 m,MAPE<13.5%,r2_score≥0.95,且SVR模型精度比BR模型更高;SB模型的精度最差,训练集和验证集的RMSE>2 m,MAPE>1.5 m,MAPE>38%,r2_score<0.7.

表3 John Brewer Reef水深反演整体精度评价Table 3 Overall accuracy evaluation of bathymetry inversion in John Brewer Reef

表4 Fitzroy Reef水深反演整体精度评价Table 4 Overall accuracy evaluation of bathymetry inversion in Fitzroy Reef
由于水深范围和数据量不同,Fitzroy Reef研究区的整体反演精度比John Brewer Reef研究区略差.在Fitzroy Reef研究区,与John Brewer Reef研究区一致,RF模型拟合效果最好,训练集RMSE=0.55 m,MAE=0.26 m,MAPE=7.53%,r2_score=0.99,但存在一定程度的过拟合;MLP、高阶多项式、RF的测试集精度最高,其中MLP和CP模型的测试集精度达到了RMSE=0.79 m,MAE=0.39 m,r2_score=0.98;SVR、LP模型精度次之,训练集和测试集精度RMSE<1.2 m,MAE 0.75 m,MAPE<31%,r2_score≥0.96,与John Brewer Reef研究区不同的是,SVR模型的精度高于LP模型,原因是当数据量增多,水深范围变大时,虽然基于BR模型,非线性的SVR模型相比于线性的低阶多项式模型具有更好的反演能力.
综合两个研究区的水深反演精度:MLP、高阶多项式、RF的水深反演精度最高,其中,RF模型拟合效果最好,但容易出现一定程度的过拟合现象;SVR模型、LP模型精度次之,且当数据量增多,水深范围变大时,非线性的SVR模型相比于线性的低阶多项式模型具有更好的反演能力;BR模型精度较低,SB模型的精度最差,均不适合用于实际水深反演.
4.2.4 模型反演深度分析
与John Brewer Reef不同,在Fitzroy Reef,MLP和RF模型反演水深最大值同多项式模型一样,均达到了23 m以上,见表5.对比分析MLP和RF模型在两个研究区的不同表现,这是John Brewer Reef研究区的水深样本最大深度只有13.907 m导致的,同时说明MLP和RF模型存在一定程度的过拟合,高度依赖水深样本分布.虽然3种多项式模型在深水区域均有不错的反演表现,当多项式阶次过高时,多项式模型的反演结果严重发散,极其不稳定,如在John Brewer Reef,QP和CP的反演水深最大值分别达到了27.658 m和45.818 m,与真实的水下地形严重不符.

表5 8种模型反演的水深范围Table 5 Water depth range of bathymetric inversion based on eight models
5 结论与建议
(1)基于光子点群的高斯分布特征进行海面光子点提取,可以有效处理具有多种多样光子点分布的波束轨迹条带,对不同轨迹长度、不同海面起伏度的情况均有较好的适应性.海底光子点群密度随深度增加而减少的先验信息有助于海底光子点群提取,在DBSCAN聚类算法基础上引入深度自适应和滑动窗口可以有效提高海底光子点群的提取效率和准确率.
(2)以Parrish折射改正几何模型为基础,考虑海面倾斜造成的入射角偏移,可以进一步改正水体折射效应对水深测量造成的影响.折射改正后光子点水深呈整体变浅,且水深越深,变浅越多的线性规律,改正项约为改正前水深的0.2550倍.
(3)结合ICESat-2数据和Sentinel-2影像在水质清澈的浅海域进行主被动融合水深反演效果较好.相比其他水深实测数据,ICESat-2测深数据具有高度一致性,这直接导致利用ICESat-2水深值进行水深反演的精度更高,可靠性更好.在众多水深反演模型中,SB模型和BR模型反演精度较差,多项式模型和MLP、RF等机器学习模型反演效果相比于BR模型和SVR模型,反演效果更好,但MLP和RF模型的反演效果对水深样本分布具有高度依赖性,且RF模型往往出现过拟合.当区域ICESat-2水深样本丰富、深度范围宽广时,MLP模型是较为理想的可靠反演模型,而当区域ICESat-2水深深水样本不足或先验信息匮乏时,LP模型是相对稳妥的选择.
致谢感谢审稿专家提出的修改意见和编辑部的大力支持!
