叶片穿孔数对冷却风扇气动性能和噪声性能的影响研究*

2024-03-11王华伟刘汉阳

机电工程 2024年2期

王华伟,王砾,刘汉阳,王博,胡溧

(1.武汉科技大学汽车与交通工程学院,湖北武汉 430070;2.中国船舶集团有限公司第七二二研究所,湖北武汉 430223)

0 引言

随着发动机性能的不断提高与车用电器功率需求的日益增加,对发动机冷却系统散热性能的要求也越来越高。采用尺寸更大、转速更高的冷却风扇无疑是最直接的方法,但是其噪声、成本也会相应增加。

随着对汽车噪声、振动与声振粗糙度(noise、vibration、harshness,NVH)要求的不断提高,冷却风扇噪声问题逐渐凸显。因此,研究冷却风扇的气动及噪声特性,探索风扇的降噪设计方法,对于性能优异的车用冷却风扇设计具有重要意义。

国内外学者在轴流风机的噪声预测与控制领域已经进行了大量的研究,并且做出了大量的贡献。

LUO Bo等人[1]对低速轴流风机叶尖泄漏流和气动声学进行了分析,并基于试验数据的对比,成功验证了数值预测的可靠性和准确性,结果表明,当叶顶间隙增大时,叶尖涡强度的增强以及与叶片表面相互作用的增强是产生额外宽频噪声的主要原因。TOKUSHIGE T等人[2-3]对环形风机气动噪声进行了研究,结果表明,通过对开口风扇增加导流环,不仅可以改善气动性能,还可以降低风扇噪声,且叶片表面的离散频率噪声是由与叶片通过频率同步的周期性压力波动产生的。YE Xue-min等人[4]针对不同锯齿后缘对单级变桨距轴流风扇气动及噪声性能的影响进行了数值模拟研究,并设计了一种具有新型锯齿叶片的低噪声轴流风扇。周敏等人[5]提出了一种在轴流式压气机叶片开孔的方法,使压力面到吸力面的压差产生射流,从而吹除叶片吸力面的附面层,增加附面层的湍流动能,并且延缓气流分离。胡勇军[6]设计了一种穿孔式双转子轴流风扇,并探究了不同穿孔参数对其性能的影响,其发现通过对叶片穿孔可有效降低双转子轴流风扇气动噪声,提升NVH性能。YANG Xing-lin等人[7]分析了叶片穿孔对大型船用轴流风机的性能影响,研究结果表明,轴流风机在叶尖区域进行开孔对离散噪声具有抑制作用;但是该研究缺少对风扇性能曲线的分析。WANG Chen等人[8]基于小型反向旋转风扇中的被动降噪技术,采用多孔后缘处理了由于两个转子之间相互作用产生的噪声,并综合考虑气动性能和噪声性能,发现应选择尽可能小的孔径和在远离叶片后缘方向上递减的穿孔率分布;但其未能精准仿真离散频率噪声。王善彬等人[9]针对后缘穿孔结构对叶片气动特性和噪声特性的影响,以NACA65019叶片为基础,采用大涡模拟和FW-H方程,研究了孔型及穿孔倾角对叶片气动特性及噪声特性的影响机理。

上述研究结果表明,叶片穿孔结构已在部分旋转机械或翼型结构改进中取得进展。但环形冷却风扇导流环与叶尖为一体式结构,离散噪声形成机理不同,穿孔降噪结构尚未应用在环形冷却风扇叶片之上。

基于以上研究,笔者采用数值模拟的方法,探究叶片穿孔数对车用环形冷却风扇气动性能和噪声性能的影响。

首先,建立准确的冷却风扇计算模型;然后,设计具有不同穿孔数的叶片结构;最后,对原风扇模型和叶片穿孔模型的流场与声场进行分析,得出其影响规律,以期为环形冷却风扇噪声控制技术提供参考。

1 FW-H声学模型

FW-H声学模型本质上是一个非均匀波动方程,可以从连续性方程和Navier-Stokes方程推导得出。FW-H声学模型主要用于噪声预测。

FW-H方程可写成:

(1)

式中:u为流体速度;un为f=0的表面法向流体速度分量;v为表面速度;vn为表面速度法向分量;ρ为流体密度;δ(f)为狄拉克函数;H(f)为亥维塞函数;p为声压;p′为远场声压,p′=p-p0;a0为远场声速;Tij为Lighthill应力张量;n为物体表面的外法矢量;下标i,j,k为xi、xj、xk方向的分量。

Tij的定义为:

(2)

式中:Pij为压缩应力张量,自由流物理量由下标0表示;δij为克罗内克符号。

对于斯托克斯流体,其表达式如下:

(3)

在声源和接收器之间没有障碍物以及自由空间流的假设下,可以对式(1)进行综合分析。

完整的解包括表面积分和体积积分。表面积分表示单极子和偶极子声源,以及部分来自四极子声源的贡献,而体积积分表示声源表面外部区域中的四极声源。当声源表面包围源区域,且流动为低亚音速时,体积积分的贡献变小。因此,式中忽略了体积积分。

远场声压可表示为:

(4)

式中:t为到接收器时间。

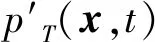
厚度噪声方程可表示为:

(5)

载荷噪声方程可表示为:

(6)

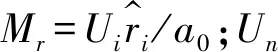
叶片表面速度可表示为:

(7)

叶片表面载荷可表示为:

(8)

2 数值模拟

2.1 流场计算

笔者以某6叶发动机环形冷却风扇作为研究对象(风扇外径为405 mm、轮毂直径为165 mm、轮毂比为0.4、叶片厚度为2 mm),使用FLUENT软件对原风扇模型进行数值模拟。

在保证计算结果准确的前提下,笔者首先对风架凸耳、加强筋和插接件等结构进行简化,并且将风扇轮毂简化为同尺寸的圆台;然后,严格按照试验条件建立计算域模型(计算域包括模拟风扇运动状态的旋转域和模拟风扇进出口通道的流体域),建立进口为边长1 m的正方体,出口则采用长为2 m、宽和高为1 m的长方体作为流体域;最后,建立直径比风扇外径略大的圆柱作为旋转域将风扇包络,以模拟其近壁面气流状态。

风扇简化模型和计算域如图1所示。

图1 数值模拟计算模型

由于冷却风扇存在复杂曲面,所以笔者采用网格划分的方式选择数值模拟精度、自适应度高的非结构化网格。

笔者利用计算资源对网格无关性进行分析(风量不随网格数量增加而变化),之后将流体域网格尺寸设置为30 mm,旋转域和风架网格尺寸设置为5 mm,叶片表面网格设置为2 mm,叶片前、后缘以及其余小尺寸部位网格设置为1 mm。

由于叶片为主要噪声源,需要在其表面建立边界层网格。其中,第一层网格高度设定为0.01 mm,总层数为20层,增长率为1.2,网格总数量约为8.5×106。

边界层局部网格示意图如图2所示。

图2 叶片网格局部放大图

笔者对照试验环境设置仿真模型的边界条件,进出口均设为压力边界,旋转域采用多运动参考系模型(multiple reference frame,MRF)[10],风扇转速按照实测工况下的转速2 270 r/min进行设置。

在稳态计算中,湍流模型采用k-ε模型[11-12],壁面函数选择兼容性更强的可放缩壁面函数(scalable)。

笔者运用SIMPLE算法求解压力速度耦合方程,控制方程的离散格式运用二阶迎风格式进行离散,收敛残差设为1×10-4,迭代步数设置为2 000步,设置进出口流量和静压等监测项,进出口流量差小于0.5%则视为收敛。

2.2 噪声计算

噪声计算的流体域是在网格尺寸不变的基础上,改为用长4 m、直径为2 m的圆柱将旋转域包裹起来。

稳态计算方式与气动性能计算保持一致,并且在稳态计算结果基础上选择大涡模拟(large eddy simulation,LES)[13]湍流模型,以便进行瞬态仿真计算,直到进出口流量计算稳定。

笔者设置与试验情况相同的噪声监测点,然后采用FW-H方程计算得到噪声监测点的声压信号;最后,应用傅里叶变换对声压信号进行处理,以获得噪声的频谱图。

由于此处主要在20 Hz～5 000 Hz频率范围内进行噪声研究,笔者结合奈奎斯特采样定理[14],设置时间步长为0.000 1 s;并且遵循保证计算准确性且节约计算资源的原则,设置总时间为0.2 s。

3 试验验证

3.1 气动性能试验

按照《工业通风机用标准化风道性能试验》(GB/T 1236-2017)[15]规定,笔者对研究对象进行气动性能测试试验。

风扇进口为管道式,出口为与外界大气相连的自由式,风扇静压可由压力传感器测得(精度为±1%);采用超声波流量计测定风量,即按照正态分布取95%的置信区间,包含因子k=2,风量扩展不确定度为:U(qv)=1.21%。

风量计算公式如下:

(9)

式中:D为管道直径,m;v为流速,m/s;c为管道内的声速,m/s;θ为流体静止时超声轨迹与管道轴线之间的夹角;Δt为顺逆流时间差,s。

笔者将冷却风扇布置于试验台架上,调节风扇工况,得到静压、风量、转速、轴功率等数据,最终计算得出风扇性能曲线。

气动性能试验台如图3所示。

图3 气动性能测试台架

笔者将试验结果与仿真结果进行对比分析,结果显示:将风量和静压效率的仿真与试验对比,各工况误差均在5%以内,满足工程应用条件。

气动性能试验与仿真结果对比如图4所示。

图4 气动性能试验与仿真结果对比

由图4可知:风量随静压的升高而减小,静压效率与仿真误差随静压增加而升高;产生误差的因素有:计算模型中对复杂结构的简化、试验仪器安装误差等。

3.2 噪声性能试验

根据《风机和罗茨鼓风机噪声测量方法》(GB/T 2888-2008)[16],笔者将风扇置于半消声室内(其中,风扇中心轴线距地面高度为1.5 m),进行噪声性能试验;同时试验所在半消声室也符合ISO3745标准。

笔者在风扇中心轴线上距离风扇中心点前后各1 m处设置两个噪声监测点,以此来采集声音信号。

声压级计算公式如下:

(10)

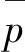
式(10)中,笔者按照正态分布取95%的置信区间,包含因子k=2,噪声扩展不确定度为U(SPL)=1.42%。

噪声试验测量环境和麦克风如图5所示。

图5 噪声性能试验

噪声性能试验设备参数如表1所示。

表1 设备名称及参数

进气侧(监测点1)处的试验与仿真的前三阶离散噪声声压级与总声压级对比如表2所示。

表2 离散噪声声压级与总声压级对比

监测点1处试验与仿真噪声频谱对比如图6所示。

图6 监测点1处噪声频谱图对比

由表2与图6可知:试验结果与仿真计算结果整体上较为一致,冷却风扇离散噪声主要集中在低频段,且最大峰值均出现在二阶离散噪声处,高频段以涡流噪声为主。

监测点处的A计权总声压级仿真结果较试验值略低。笔者分析该误差原因有:边界层网格未精确模拟叶片表面边界层运动情况;冷却风扇旋转时产生的结构振动噪声与电机运转产生的电磁噪声使噪声试验值增加。

综上可知,监测点1处的噪声值与数值计算结果误差在5%以内。由此可见,该数值模拟方法可用于进一步的风扇降噪研究。

4 结构优化

当电机驱动环形冷却风扇旋转时,在摩擦阻力的[5]作用下,其叶片吸力面表面气流改变了原有旋转方向,沿径向甩出后与导流环相互干涉形成回流;这些回流与叶片尾迹同后续叶片前缘相互作用,又形成离散频率噪声,叶片表面的漩涡脱落产生了涡流噪声[17-19]。

叶尖附近是形成低压回流的主要区域,也是离散频率噪声形成的主要部位,为此,笔者对叶尖部位进行穿孔设计,以达到降噪的目的。

穿孔定位方式如图7所示。

图7 穿孔定位方式

穿孔模型对比如图8所示。

图8 穿孔示意图

将叶片尾缘绕轮毂圆心顺时针分别旋转3°、6°和9°,可以得到三条弧线L、M、N,作为孔的周向定位方式;然后,将叶片沿径向进行15等分,取靠近导流环的两条等分线O、P作为径向定位方式,两者交点为穿孔最终定位。

模型A以弧线M与等分线O、P相交,相交的两个点作为圆心进行穿孔;模型B在模型A的基础上增加圆心为弧线L与等分线O、P交点的两个孔;模型C在模型B的基础上增加圆心为弧线N与等分线O、P交点的两个孔,穿孔半径为2 mm。

5 结果对比

5.1 气动性能对比

三种穿孔模型与原模型的气动性能对比结果如图9所示。

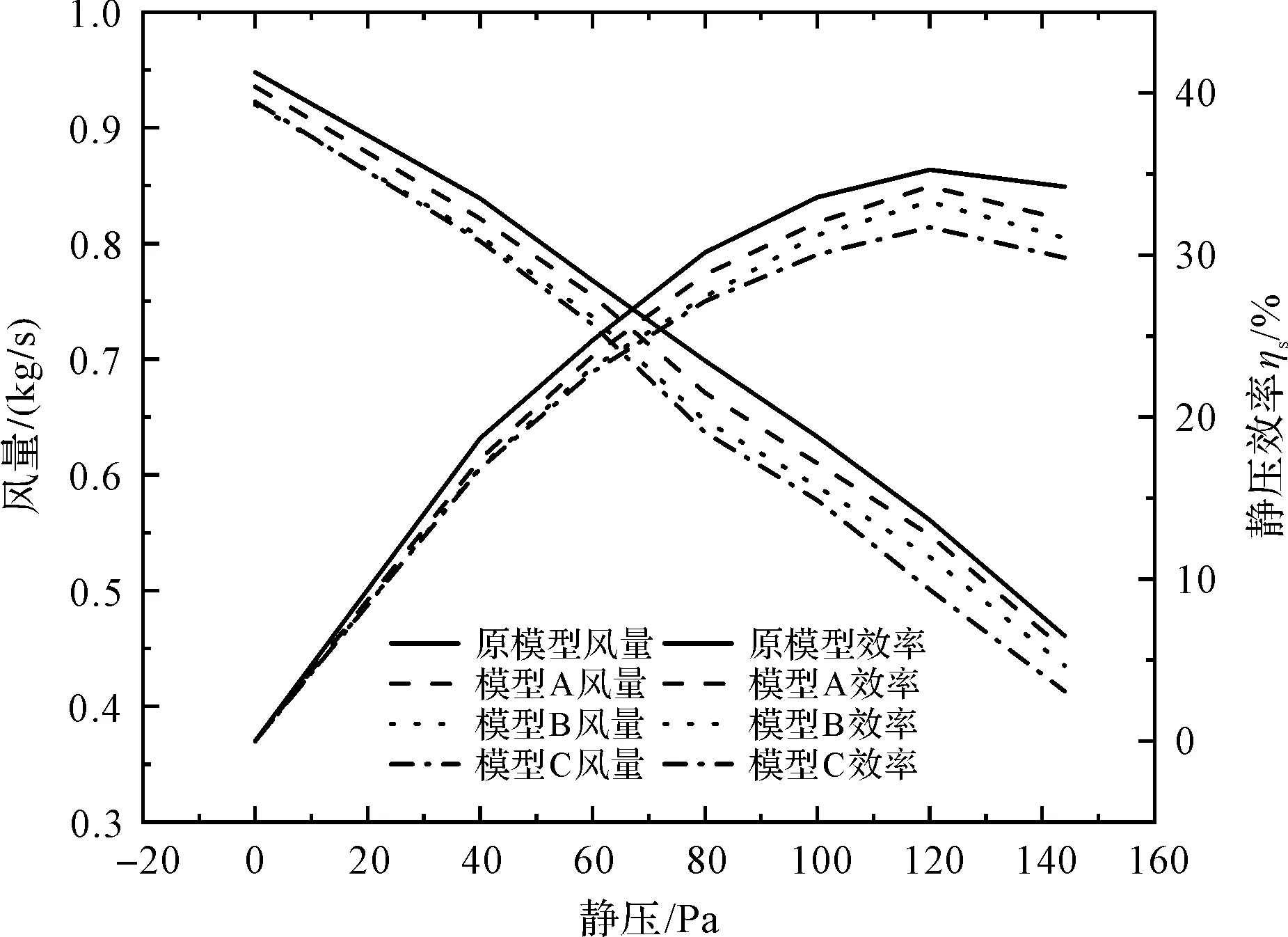
图9 气动性能对比

根据图9可知:与原模型相比,三种穿孔模型风量和静压效率随穿孔数量的增加逐渐减小。这是由于叶片压力面与吸力面压差作用,使得部分气体由压力面流向吸力面,导致气体泄漏,使得风量与静压效率下降。

叶片吸力面静压云图如图10所示。

图10 吸力面静压云图

叶尖速度矢量图如图11所示。

图11 吸力面叶尖速度矢量图

由图10和图11可知:原模型与三种优化模型叶片前缘静压达到最大,叶尖与导流环连接处出现低压区[20]。这主要是由于吸力面表面的部分气流在摩擦阻力的作用下,改变了原有旋转方向沿径向甩出,甩出后与导流环产生干涉,进而形成叶尖吸力面的低压回流区。

由于穿孔设计,部分流体从压力侧流向吸入侧形成射流,这使得叶片吸力面压力和速度分布发生变化。随着穿孔数的增加,叶尖穿孔部位低压区域减小、压力梯度减小,并且吸力面穿孔附近气流速度增大,使得边界层内的流体获得新的动能以克服摩擦阻力,因此,有效地抑制了回流的产生。

t=0.1 s时刻的涡量云图如图12所示。

图12 t=0.1 s时涡量云图

由图12可知:在导流环内圆以及叶片尾缘附近出现大量漩涡脱落现象。叶片穿孔引起的射流使边界层低速气流重新获得动能,边界层分离现象得到改善,尾缘涡量得到一定控制。但射流与吸力面融合时,穿孔位置附近也产生了部分漩涡。

模型A穿孔数量较少,尾缘附近涡量分布改善不明显;增加模型B的穿孔后,尾缘涡量明显减少;虽然模型C尾缘处涡量改善最明显,但其穿孔数量过多且射流速度高,造成气体泄漏过多,产生了额外的分离涡。

5.2 噪声性能对比

模型A、B、C与原模型噪声频谱图对比如图13所示。

图13 原模型与其他三种模型噪声频谱图对比

三种优化模型与原模型前三阶离散频率噪声声压级与总声压级对比如表3所示。

表3 原模型与其他三种模型噪声对比

由图13与表3可知:三种优化模型对风扇噪声性能的影响与压力云图展现情况一致,穿孔结构有效抑制了叶尖低压回流区的产生,使得后续叶片切割的气流更加稳定有序,从而降低了离散频率噪声(因叶片周期性切割气流而产生)。

三分之一倍频程图如图14所示。

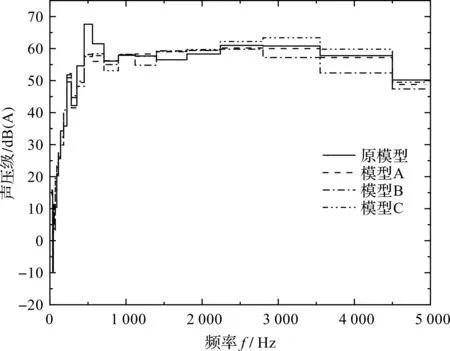
图14 三分之一倍频程图

由图14可知:宽频噪声与涡量云图情况展现一致。由此可见,穿孔设计不仅可以抑制回流的产生,并且对尾涡脱落的产生也有一定影响。

模型A由于穿孔数量较少,带来的吸力面压力和速度变化也较小,所以对高频段涡流噪声的影响同样较小;模型B穿孔数量增加,穿孔射流使得边界层内的流体获得了新的动能,以克服摩擦阻力,在一定程度上抑制了尾涡脱落,减小了高频段的涡流噪声;模型C由于穿孔数量过多,而射流速度过大,因此产生了新的分离涡,致使高频段涡流噪声有所增加。

因此,数量适当的穿孔设计可以有效降低环形冷却风扇的气动噪声。